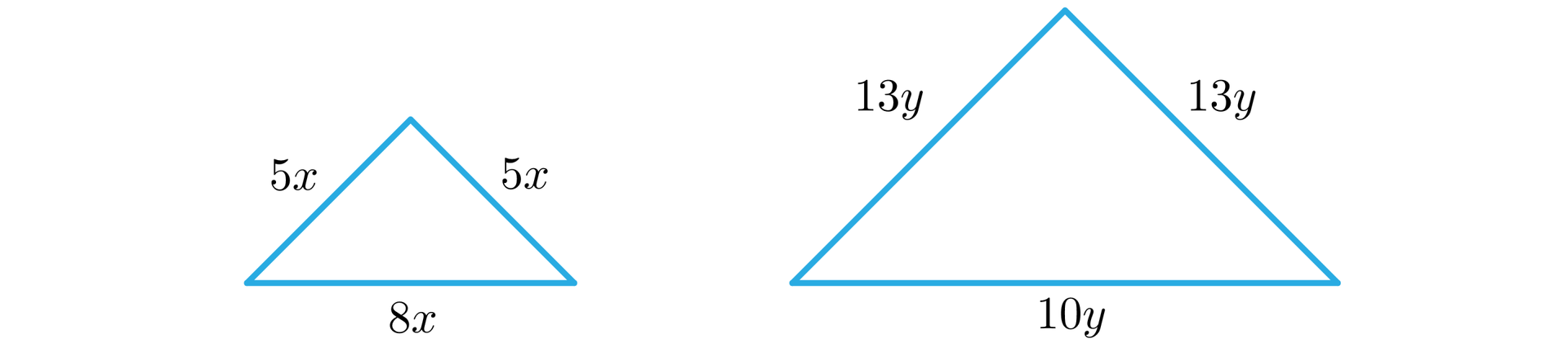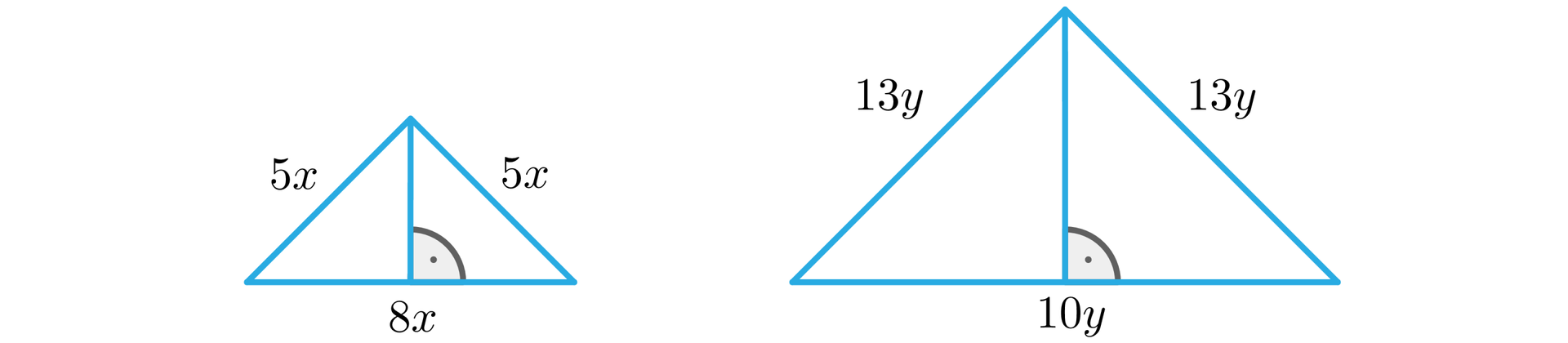Sprawdź się
Która z funkcji osiąga maksimum, a która osiąga minimum? Przeciągnij wzory w odpowiednie miejsca.
<span aria-label="f nawias, x, zamknięcie nawiasu, równa się, minus, dwa nawias, x, minus, cztery, zamknięcie nawiasu, indeks górny, dwa, plus, pięć" role="math"><math><mi>f</mi><mfenced><mi>x</mi></mfenced><mo>=</mo><mo>-</mo><mn>2</mn><msup><mfenced><mrow><mi>x</mi><mo>-</mo><mn>4</mn></mrow></mfenced><mn>2</mn></msup><mo>+</mo><mn>5</mn></math></span>, <span aria-label="f nawias, x, zamknięcie nawiasu, równa się, minus, dwa x indeks górny, dwa, plus, trzy x, plus, cztery" role="math"><math><mi>f</mi><mfenced><mi>x</mi></mfenced><mo>=</mo><mo>-</mo><mn>2</mn><msup><mi>x</mi><mn>2</mn></msup><mo>+</mo><mn>3</mn><mi>x</mi><mo>+</mo><mn>4</mn></math></span>, <span aria-label="f nawias, x, zamknięcie nawiasu, równa się, dwa nawias, cztery, minus, x, zamknięcie nawiasu, indeks górny, dwa, minus, pięć" role="math"><math><mi>f</mi><mfenced><mi>x</mi></mfenced><mo>=</mo><mn>2</mn><msup><mfenced><mrow><mn>4</mn><mo>-</mo><mi>x</mi></mrow></mfenced><mn>2</mn></msup><mo>-</mo><mn>5</mn></math></span>, <span aria-label="f nawias, x, zamknięcie nawiasu, równa się, trzy nawias, x, plus, pięć, zamknięcie nawiasu, nawias, dwa, minus, x, zamknięcie nawiasu" role="math"><math><mi>f</mi><mfenced><mi>x</mi></mfenced><mo>=</mo><mn>3</mn><mfenced><mrow><mi>x</mi><mo>+</mo><mn>5</mn></mrow></mfenced><mfenced><mrow><mn>2</mn><mo>-</mo><mi>x</mi></mrow></mfenced></math></span>, <span aria-label="f nawias, x, zamknięcie nawiasu, równa się, minus, dwa nawias, jeden, minus, x, zamknięcie nawiasu, nawias, x, minus, trzy, zamknięcie nawiasu" role="math"><math><mi>f</mi><mfenced><mi>x</mi></mfenced><mo>=</mo><mo>-</mo><mn>2</mn><mfenced><mrow><mn>1</mn><mo>-</mo><mi>x</mi></mrow></mfenced><mfenced><mrow><mi>x</mi><mo>-</mo><mn>3</mn></mrow></mfenced></math></span>, <span aria-label="f nawias, x, zamknięcie nawiasu, równa się, cztery nawias, x, plus, jeden, zamknięcie nawiasu, indeks górny, dwa, minus, pięć" role="math"><math><mi>f</mi><mfenced><mi>x</mi></mfenced><mo>=</mo><mn>4</mn><msup><mfenced><mrow><mi>x</mi><mo>+</mo><mn>1</mn></mrow></mfenced><mn>2</mn></msup><mo>-</mo><mn>5</mn></math></span>, <span aria-label="f nawias, x, zamknięcie nawiasu, równa się, x indeks górny, dwa, minus, dwa x, plus, jeden" role="math"><math><mi>f</mi><mfenced><mi>x</mi></mfenced><mo>=</mo><msup><mi>x</mi><mn>2</mn></msup><mo>-</mo><mn>2</mn><mi>x</mi><mo>+</mo><mn>1</mn></math></span>
| maksimum | |
|---|---|
| minimum |
Obwód prostokąta wynosi . Jakie wymiary powinien mieć prostokąt, aby jego pole było jak największe?
Jaka liczba dodana do swojego kwadratu tworzy najmniejszą sumę?
Wskaż wykres, z którego można odczytać rozwiązanie zadania: Jaka jest możliwa największa wartość iloczynu dwóch liczb, których suma jest równa ?
- Opis ilustracji A
- Opis poprawnej ilustracji B
- Opis ilustracji C
- Opis ilustracji D
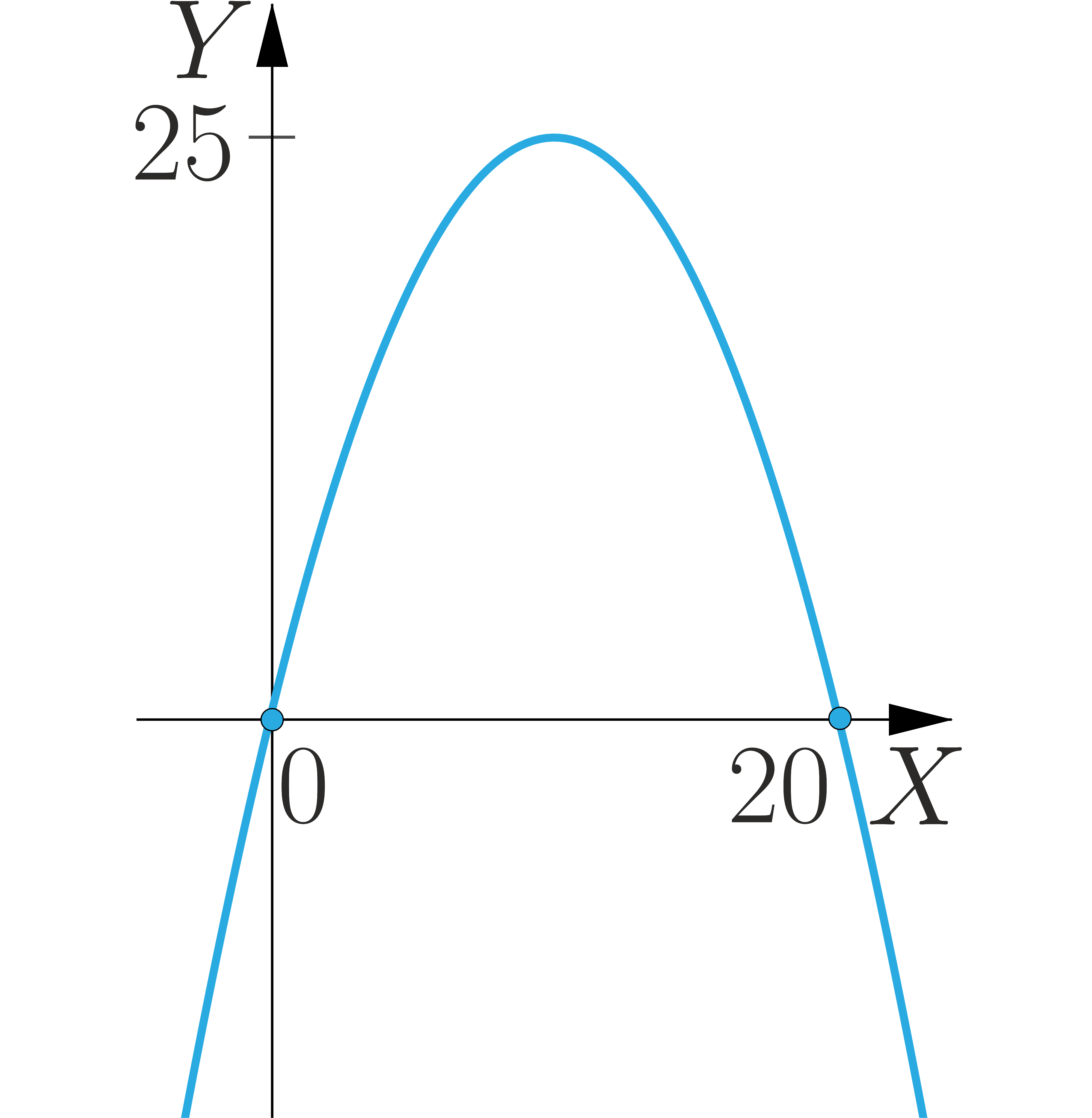
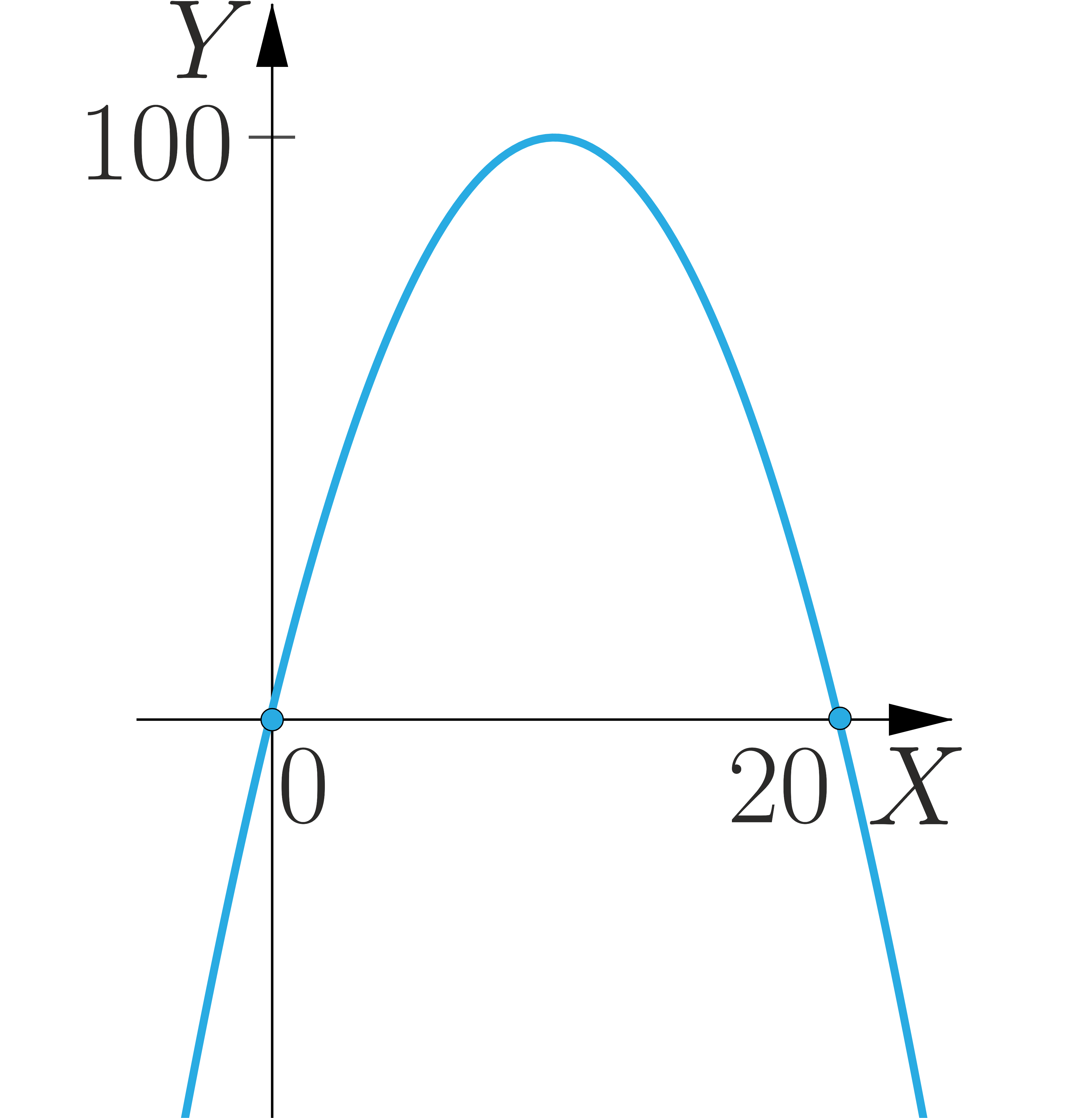
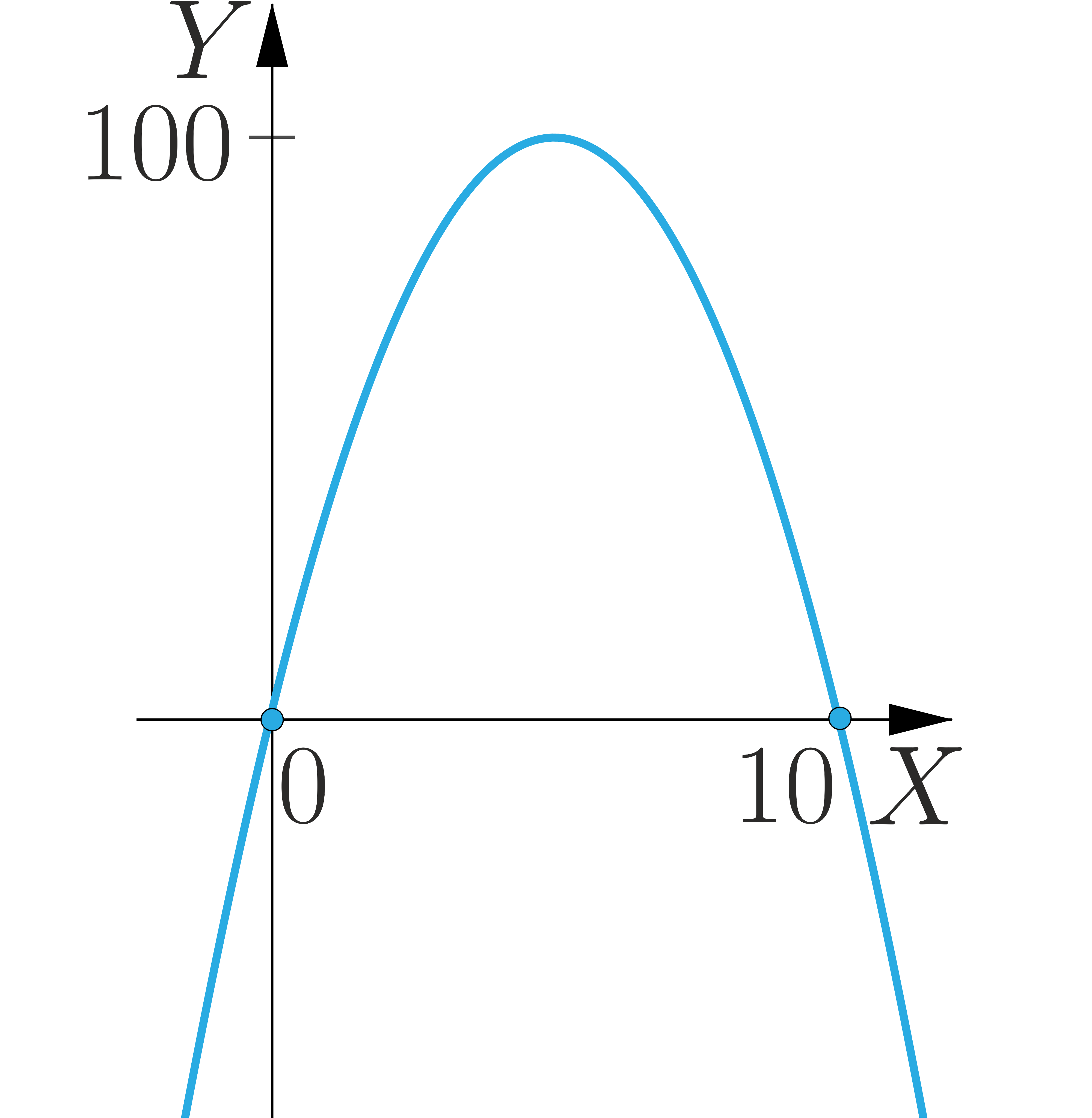
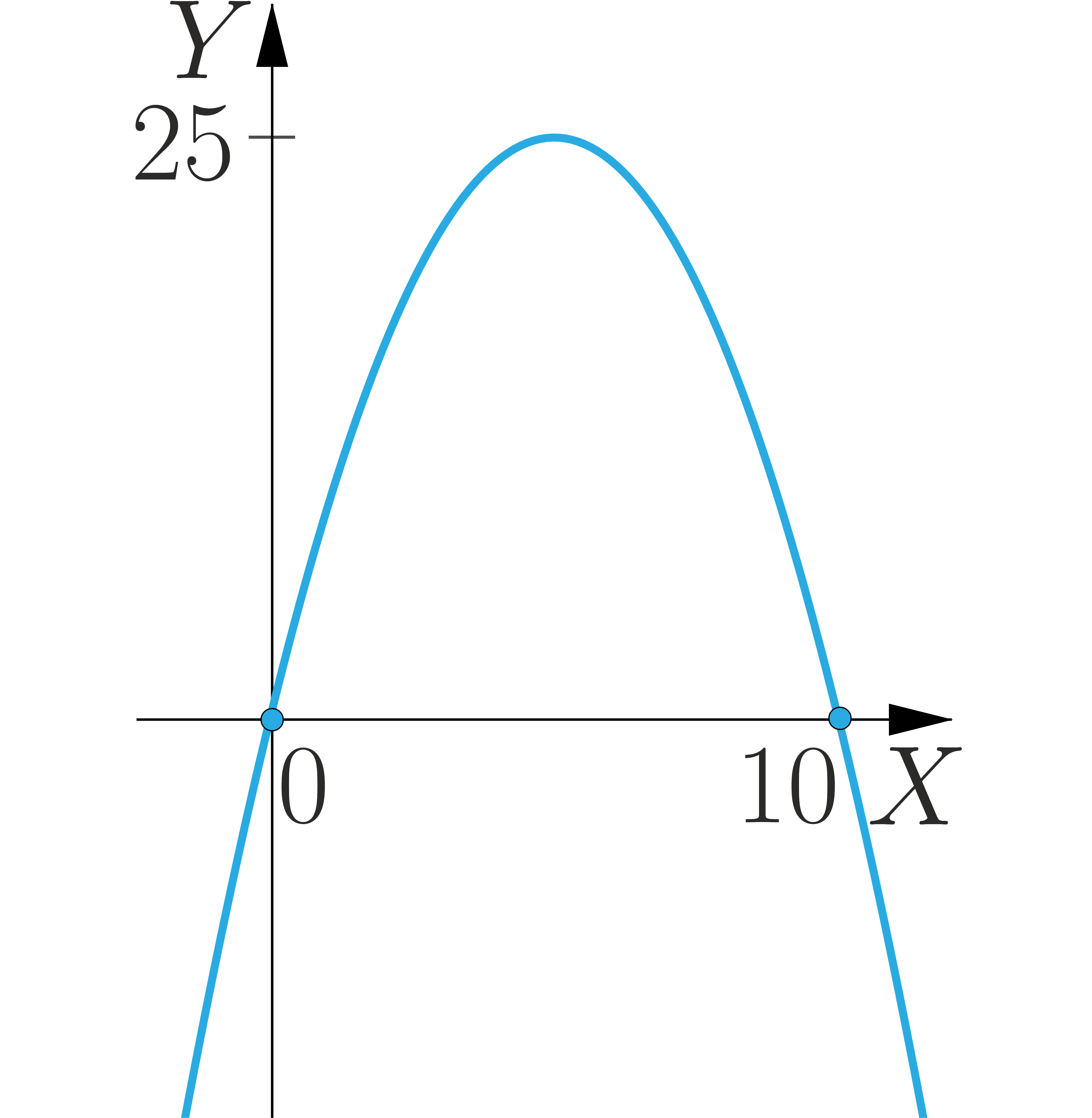
Na prostej o równaniu znajdź taki punkt o dodatnich współrzędnych, że iloczyn odległości punktu od osi układu współrzędnych jest największy z możliwych.
Dane są punkty i . Na osi znajdź taki punkt , aby suma kwadratów długości odcinków i była najmniejsza.
Drut o długości rozcięto na dwa kawałki i z każdego kawałka zbudowano brzeg trójkąta równoramiennego, przy czym stosunek długości ramienia do długości podstawy w jednym trójkącie wynosi , a w drugim . Jakie obwody mają te trójkąty, jeżeli suma ich pól jest najmniejsza z możliwych?