Symetria osiowa względem osi X i osi Y. Zadania - część I

Pokaż ćwiczenia:

Przypomnij sobie najważniejsze informacje dotyczące symetrii względem osi $X$ i $Y$ .

Obraz odcinka $A B$ w symetrii względem osi $X$ i osi $Y$ .

RL5GqAm1KcPCx

Ilustracja przedstawia układ współrzędnych z poziomą osią X od minus 6 do 6 oraz z pionową osią Y od minus czterech do czterech. Na płaszczyźnie narysowano odcinek o końcach w punktach A=(-2, 3) i B=(4, 1), odcinek do niego symetryczny względem osi X o końcach w punktach A1=(-2, -3) i B1=(4, -1) oraz odcinek do niego symetryczny względem osi Y o końcach w punktach A2=(2, 3) i B2=(-4, -1). — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Obraz funkcji $f (x)$ w symetrii względem osi $X$ .

R1Z05jqpcZSp3

Ilustracja przedstawia układ współrzędnych z poziomą osią X od minus 6 do 6 oraz z pionową osią Y od minus 5 do 5. Na płaszczyźnie narysowano funkcję fx o nieregularnym kształcie i jej obraz w symetrii względem osi X. Otrzymana funkcja, to -fx. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Obraz funkcji $f (x)$ w symetrii względem osi $Y$ .

RIeXN1MeGwhY6

Symetria wykresu funkcji względem osi

X

Y

Twierdzenie: Symetria wykresu funkcji względem osi

X

Y

Wykres funkcji $y = - f (x)$ powstaje w wyniku przekształcenia wykresu funkcji $y = f (x)$ przez symetrię osiową względem osi $X$ .
Wykres funkcji $y = f (- x)$ powstaje w wyniku przekształcenia wykresu funkcji $y = f (x)$ przez symetrię osiową względem osi $Y$ .

RFxSNZLKFmZAk1

Ćwiczenie 1

odcinek, który ma jeden punkt wspólny z osią $Oy$
odcinek, którego jednym z końców jest punkt $(- 2, 5)$
odcinek, którego jeden z końców leży na osi $Ox$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RdFOaWbWz4QFF1

Ćwiczenie 2

leży na osi $Oy$
leży na osi $Ox$
ma obie współrzędne ujemne

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1F5Gacxwcpd31

Ćwiczenie 3

okrąg o promieniu $4$
okrąg, którego środkiem jest punkt $(2, 4)$
okrąg, który ma trzy punkty wspólne z osiami układu współrzędnych

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 4

RjJOqc6x7zlaU

Określ, czy podane funkcje są symetryczne względem osi

Y

, czy początku układu współrzędnych. Przeciągnij wzory funkcji do odpowiedniej grupy. funkcje symetryczne względem osi

Y

Możliwe odpowiedzi: 1.

y = - 3 x

, 2.

y = x^{3}

, 3.

y = \sqrt{x^{2}}

, 4.

y = 2 x

, 5.

y = \frac{1}{2}

, 6.

y = 2^{\sqrt{x^{2}}}

, 7.

y = x^{4}

, 8.

y = \sqrt[3]{x}

, 9.

y = x^{2}

, 10.

y = - x^{2}

, 11.

y = - 3 x^{2}

, 12.

y = \frac{1}{x}

funkcje symetryczne względem początku układu współrzędnych Możliwe odpowiedzi: 1.

y = - 3 x

, 2.

y = x^{3}

, 3.

y = \sqrt{x^{2}}

, 4.

y = 2 x

, 5.

y = \frac{1}{2}

, 6.

y = 2^{\sqrt{x^{2}}}

, 7.

y = x^{4}

, 8.

y = \sqrt[3]{x}

, 9.

y = x^{2}

, 10.

y = - x^{2}

, 11.

y = - 3 x^{2}

, 12.

y = \frac{1}{x}

Przeciągnij wzory funkcji z dolnej sekcji do górnej.

funkcje symetryczne względem osi $O y$
funkcje symetryczne względem początku układu współrzędnych

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Pamiętaj, że przekształcając wykres funkcji $y = f (x)$ w symetrii względem osi $Y$ otrzymujemy wykres funkcji $y = f (- x)$ , a przekształcając wykres funkcji $y = f (x)$ w symetrii względem początku układu współrzędnych otrzymujemy wykres funkcji $y = - f (- x)$ .

Ćwiczenie 5

R6prpu9DLVmCC

$C = (- 7, 6)$
obwód tego prostokąta wynosi $26$
pole tego prostokąta jest równe $168$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 6

RyYR36TU7T9cB

$M = (8, 9)$
wysokość tego trapezu ma długość $20$
pole trapezu jest równe $260$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 7

Na rysunku przedstawiony jest wykres funkcji $f$ .

RLve18xhOtmmk1

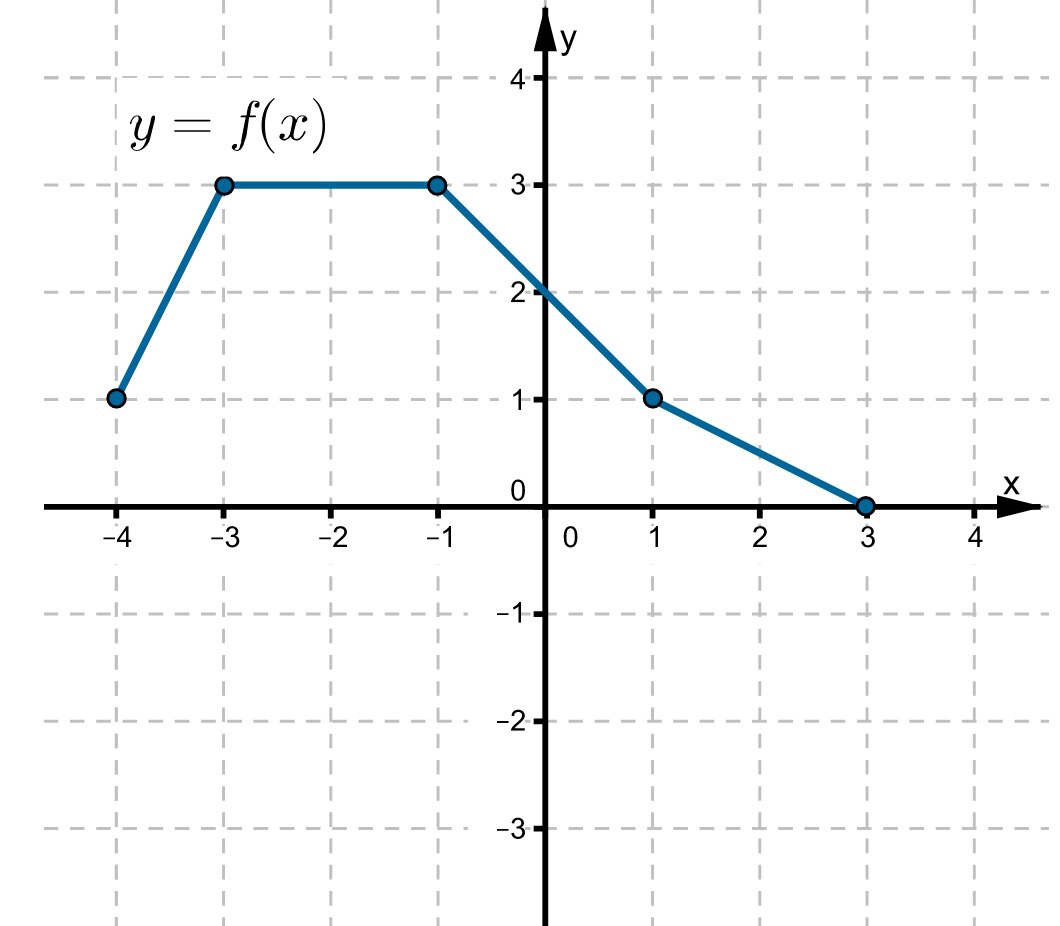
Wykres funkcji w postaci łamanej złożonej z czterech odcinków leżącej w pierwszej i drugiej ćwiartce układu współrzędnych. Do wykresu funkcji należą punkty o współrzędnych (-4, 1), (-3, 3), (-1, 3), (0, 2), (1, 1), (3, 0). — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Wyznacz wzór funkcji, której wykres przedstawiony jest na rysunku $I$ .

RlEwkwHvAhilb1

Wykres otrzymany po przekształceniu funkcji w symetrii względem osi X leżący w trzeciej i czwartej ćwiartce układu współrzędnych. Do wykresu funkcji należą punkty o współrzędnych (-4, -1), (-3, -3), (-1, -3), (0, -2), (1, -1), (3, 0). — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1WXNTm2SJK6O

$y = f (- x)$
$y = - f (x)$
$y = - f (- x)$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 8

Na rysunku przedstawiony jest wykres funkcji $f$ .

RLve18xhOtmmk1

Wyznacz wzór funkcji, której wykres przedstawiony jest na rysunku $II$ .

Rl5AvxM65PGba1

Wykres otrzymany po przekształceniu funkcji w symetrii względem osi Y leżący w pierwszej i drugiej ćwiartce układu współrzędnych. Do wykresu funkcji należą punkty o współrzędnych (-3, 0), (-1, 1), (0, 2), (1, 3), (3, 3), (4, 1). — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RlJdmXPVihZJ6

$y = f (- x)$
$y = - f (x)$
$y = - f (- x)$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 9

Na rysunku przedstawiony jest wykres funkcji $f$ .

RLve18xhOtmmk1

Wyznacz wzór funkcji, której wykres przedstawiony jest na rysunku $III$ .

R1easPyosjDyn1

Wykres otrzymany po przekształceniu funkcji w symetrii względem początku układu współrzędnych leżący w trzeciej i czwartej ćwiartce układu współrzędnych. Do wykresu funkcji należą punkty o współrzędnych (-3, 0), (-1, -1), (-2, 0), (1, -3), (3, -3), (4, -1). — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RFZ5U5zcoeymH

$y = f (- x)$
$y = - f (x)$
$y = - f (- x)$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 10

Na rysunku przedstawiony jest wykres funkcji $f$ .

R1cJwzM7YCNqW1

Wykres w postaci krzywej leżącej w pierwszej i drugiej ćwiartce układu współrzędnych. Do wykresu funkcji należą punkty o współrzędnych (1, 1), (2, 0), (3,1). — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Wyznacz wzór funkcji, której wykres przedstawiony jest na rysunku $I$ .

RfiiUz8fzt46h1

R1B2PIs5ru5xh

$y = f (- x)$
$y = - f (x)$
$y = - f (- x)$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 11

Na rysunku przedstawiony jest wykres funkcji $f$ .

R1cJwzM7YCNqW1

Wyznacz wzór funkcji, której wykres przedstawiony jest na rysunku $II$ .

RWwC7XTsvEu9h1

RMILqVBI0xrfI

$y = f (- x)$
$y = - f (x)$
$y = - f (- x)$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 12

Na rysunku przedstawiony jest wykres funkcji $f$ .

R1cJwzM7YCNqW1

Wyznacz wzór funkcji, której wykres przedstawiony jest na rysunku $III$ .

R1Khzffj1WqXU1

R7HTRfbHS33y4

$y = f (- x)$
$y = - f (x)$
$y = - f (- x)$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 13

RtxZgNoIMrxvD1

Wykres funkcji $f$ jest symetryczny względem osi $Oy$ .
Przekształcając wykres funkcji $f$ w symetrii względem osi $Ox$ , otrzymamy wykres funkcji $g (x) = - x^{4} + 4 x^{3}$ .
Przekształcając wykres funkcji $f$ w symetrii względem osi $Oy$ , otrzymamy wykres funkcji $h (x) = - x^{4} - 4 x^{3}$ .

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Pamiętaj, że przekształcając wykres funkcji $y = f (x)$ w symetrii względem osi $X$ otrzymujemy wykres funkcji $y = - f (x)$ , a przekształcając wykres funkcji $y = f (x)$ w symetrii względem osi $Y$ otrzymujemy wykres funkcji $y = f (- x)$ . Ponadto wykres funkcji $f$ jest symetryczny względem osi $Y$ , jeżeli funkcja ta spełnia dla dowolnej liczby rzeczywistej $x$ równanie $f (x) = f (- x)$ .

Ćwiczenie 14

RQKzlWp3CbMXI1

$f_{1} (x) = x^{2} + 2$
$f_{2} (x) = \frac{1}{x^{4} + 2}$
$f_{3} (x) = - x^{5} + 2 x^{3}$
$f_{4} (x) = 2 x - 5$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Pamiętaj, że wykres funkcji $f$ jest symetryczny względem osi $Y$ , jeżeli funkcja ta spełnia dla dowolnej liczby rzeczywistej $x$ równanie $f (x) = f (- x)$ .

R24CnKs7P48Ey3

Ćwiczenie 15

Istnieją takie wartości $a$ i $b$ , że wykres funkcji $f$ jest symetryczny względem osi $Oy$ .
Istnieją takie wartości $a$ i $b$ , że wykres funkcji $f$ jest symetryczny względem osi $Ox$ .
Istnieją takie wartości $a$ i $b$ , że wykres funkcji $f$ nie ma punktów wspólnych z wykresem funkcji $y = f (- x)$ .

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 16

R1P6ZzvVYj7kt

$AB$
$BC$
$CA$
$DB$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Zauważ, że odległość obu punktów od osi $Y$ musi być taka sama.

Ćwiczenie 17

RkSDzqc8uEOdq

$(- 2, 0)$
$(2, 0)$
$(0, - 5)$
$(0, 2)$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Zauważ, że pierwsza współrzędna wierzchołka $C$ musi być równa $0$ .

Ćwiczenie 18

R10CWkPNYO0pb

Okrąg o środku w punkcie $S = (2, - 2)$ i promieniu równym $2$ .
Okrąg o środku w punkcie $S = (- 2, 0)$ i promieniu równym $2$ .
Okrąg o środku w punkcie $S = (0, 3)$ i promieniu równym $2$ .
Okrąg o środku w punkcie $S = (0, 3)$ i promieniu równym $3$ .

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Zauważ, że druga współrzędna środka tego okręgu musi być równa $0$ .