Twierdzenie Pitagorasa
Analizując treści zawarte w tym materiale, poznasz twierdzenie Pitagorasa, twierdzenie odwrotne do twierdzenia Pitagorasa i niektóre zastosowania tych twierdzeń.
W trójkącie prostokątnym suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej
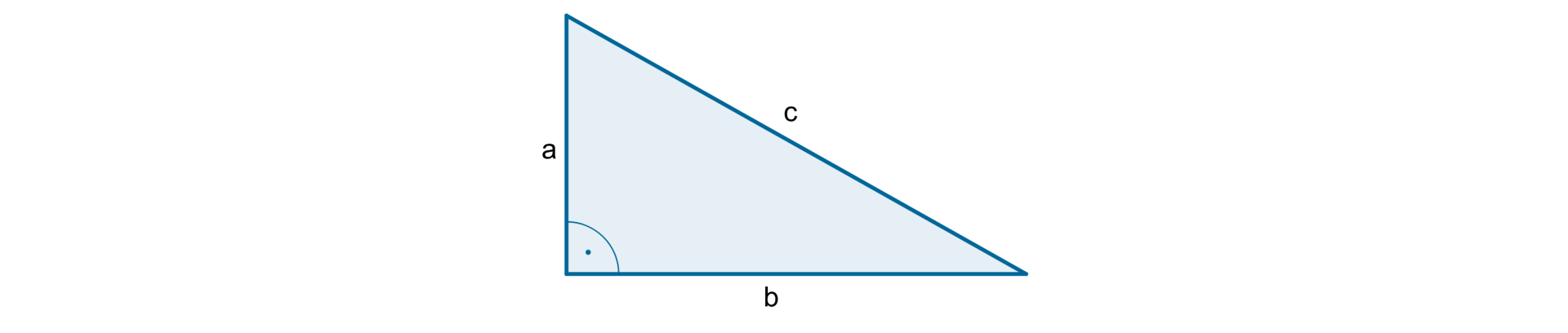
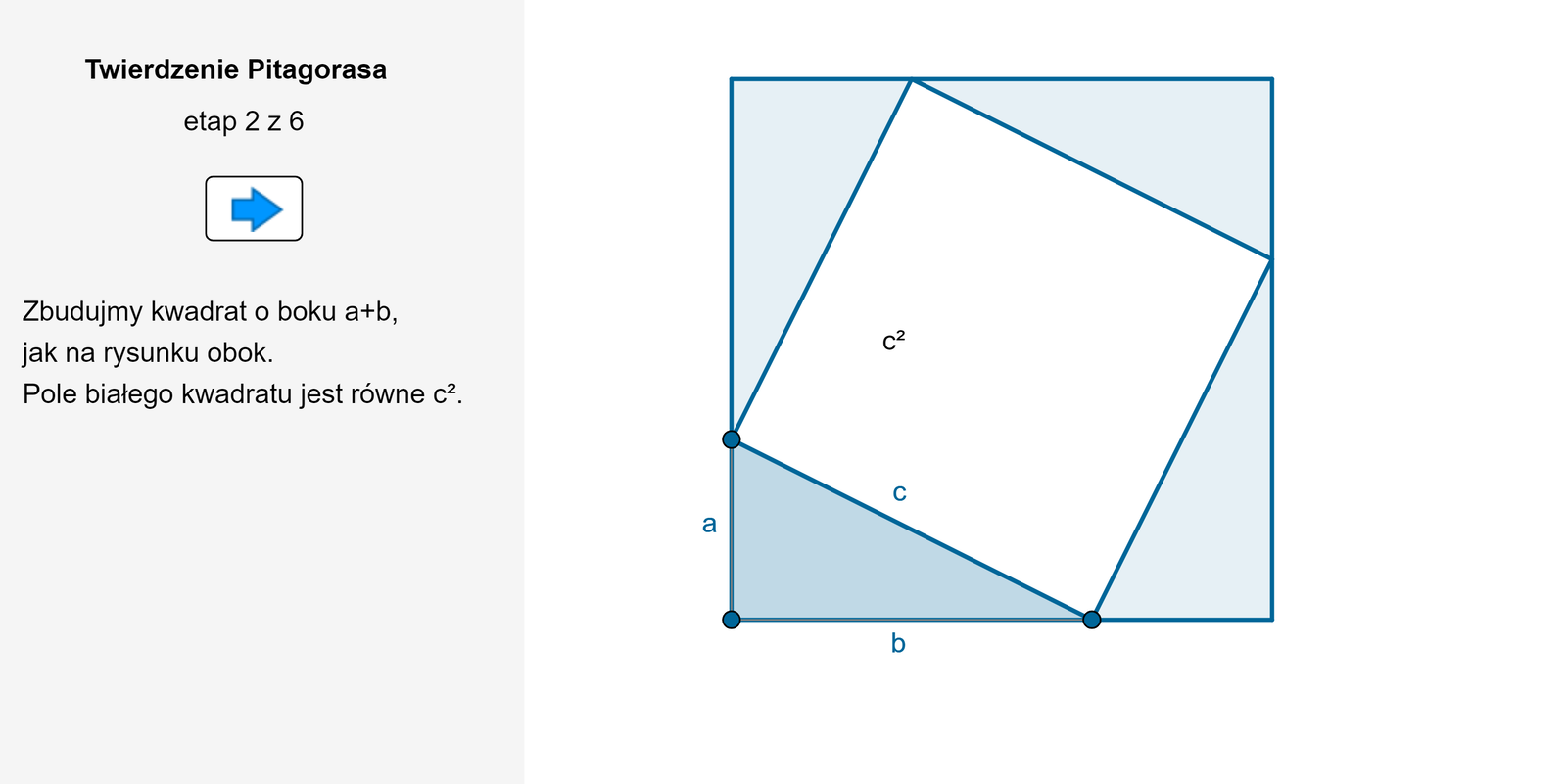
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/P16rnUviM
Prawdziwe jest też twierdzenie odwrotne do Twierdzenia Pitagorasa.
Jeżeli suma kwadratów długości dwóch boków trójkąta jest równa kwadratowi długości trzeciego boku, to trójkąt jest prostokątny.
Sprawdź, czy trójkąt o bokach , i jest trójkątem prostokątnym.
Jeżeli trójkąt będzie prostokątny, to przeciwprostokątną będzie najdłuższy z boków. Obliczmy kwadraty długości boków.
, , i zauważmy, że
Zatem z twierdzenia odwrotnego do twierdzenia Pitagorasa wynika, że ten trójkąt jest trójkątem prostokątnym.
Związki miarowe wynikające z twierdzenia Pitagorasa

Przekątna w kwadracie o boku ma długość
Zatem w trójkącie równoramiennym prostokątnym długości boków pozostają w zależności.

Rozważmy teraz trójkąt równoboczny o boku . Jego wysokość liczymy w następujący sposób
Pole trójkąta równobocznego o boku jest więc równe

Oznaczmy przez najkrótszy z boków trójkąta prostokątnego, w którym kąty ostre mają miary i . Wtedy długości boków tego trójkąta są równe , , . O takim trójkącie mówi się czasami, że jest to „trójkąt piękny”.
