Tworzenie wyrażeń algebraicznych

RXrpSDnxok7Mr

Słowo „wzór” ma wiele znaczeń. Na przykład wzór kulturowy to ustalony sposób zachowania się i myślenia w danej zbiorowości. Wzór kwiatowy to zapis służący do przedstawiania budowy kwiatu za pomocą symboli, liter i liczb. Wzór to też rysunek, motyw odbity lub wyhaftowany w celu ozdobienia czegoś. Wzorem może być osoba lub rzecz, którą warto naśladować. W matematyce wzorem określa się ciąg symboli wyrażający prawo matematyczne.

Wzory matematyczne najczęściej przedstawiane są za pomocą wyrażeń algebraicznych. Jak tworzymy, zapisujemy i odczytujemy wyrażenia algebraiczne dowiesz się, analizując przykłady zawarte w tym materiale. Sprawdzisz ukształtowane umiejętności – rozwiązując problemy zawarte w ćwiczeniach.

Interaktywna treść merytorycznaInteraktywna treść merytoryczna
Prezentacja multimedialnaPrezentacja multimedialna
Zestaw ćwiczeń interaktywnychZestaw ćwiczeń interaktywnych
SłownikSłownik

Twoje cele

Podasz przykład wyrażenia algebraicznego.
Odczytasz dane wyrażenie algebraiczne.
Zapiszesz wyrażenie algebraiczne określone słownie.
Utworzysz wyrażenie algebraiczne na podstawie informacji osadzonych w kontekście praktycznym.
Zapiszesz zależności przedstawione w zadaniach w postaci wyrażeń algebraicznych jednej lub kilku zmiennych.

Wyrażenia typu $7 + 9$ , $(24 - 3) : 5$ , $10 \cdot 2$ to wyrażenia arytmetyczne. W wyrażeniach arytmetycznych występują liczby, znaki działania, nawiasy.
Bardzo często posługujemy się wyrażeniami zawierającymi również litery. Na przykład obwód $L$ prostokąta o bokach długości $a$ , $b$ możemy obliczyć, korzystając ze wzoru:
$L = 2 \cdot a + 2 \cdot b$ .

Wyrażenie zbudowane z liczb, liter, znaków działań, nawiasów nazywamy wyrażeniem algebraicznymwyrażenie algebraicznewyrażeniem algebraicznym.

Ważne!

Pojedyncza liczba lub litera też jest wyrażeniem algebraicznymwyrażenie algebraicznewyrażeniem algebraicznym.

Ru3rPTsgIvCtC

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Przykład 1

Podamy przykłady wyrażeń algebraicznych
Wyrażenie algebraiczne	Komentarz
$4$	pojedyncza liczba
$k$	pojedyncza litera
$- 5 \cdot a \cdot b$	iloczyn liczb i liter
$f + 7 - g - 18$	liczby i litery połączone znakami działań
$6 \cdot (a - b) : d + (90 - d)$	liczby i litery połączone znakami działań i nawiasami

Litery występujące w wyrażeniach algebraicznychwyrażenie algebraicznewyrażeniach algebraicznych nazywamy zmiennymi. Jeżeli w wyrażeniu algebraicznymwyrażenie algebraicznewyrażeniu algebraicznym zmiennezmiennezmienne zastąpimy konkretnymi liczbami i wykonamy działania występujące w tym wyrażeniu, to otrzymamy wartość liczbową tego wyrażenia.

Przykład 2

Obliczymy wartość liczbową wyrażenia $2 \cdot (x - y) + x^{2}$ dla $x = 3$ , $y = (- 2)$ . Zastępujemy zmienną $x$ liczbą $3$ , a zmienną $y$ liczbą $(- 2)$ . Obliczenia wykonujemy, pamiętając o właściwej kolejności wykonywania działań.

2 \cdot [3 - (- 2)] + 3^{2} = 2 \cdot 5 + 9 = 10 + 9 = 19

Odpowiedź:
Wartość liczbowa wyrażenia jest równa $19$ .

W wyrażeniach algebraicznychwyrażenie algebraicznewyrażeniach algebraicznych typu: $7 \cdot x$ , $5 \cdot x \cdot y$ , $8 \cdot (x - y)$ , $(x + y) \cdot (x^{2} + y)$ możemy pominąć znak mnożenia. Zapisujemy wtedy: $7 x$ , $5 x y$ , $8 (x - y)$ , $(x + y) (x^{2} + y)$ .

W wyrażeniach typu: $(4 - a) : (a + b)$ , $a^{2} : 11$ możemy znak dzielenia zastąpić kreską ułamkową. Zapisujemy wtedy: $\frac{4 - a}{a + b}$ , $\frac{a^{2}}{11}$ . Zauważ, że w pierwszym przypadku opuściliśmy też nawiasy.

Gdy w wyrażeniu algebraicznymwyrażenie algebraicznewyrażeniu algebraicznym występuje dzielenie, określamy, dla jakich liczb ma ono wartość liczbową.

Na przykład wyrażenie $x - 10$ dla $x = 10$ ma wartość zero. Zatem, na przykład, wyrażenie $\frac{8}{x - 10}$ dla $x = 10$ nie ma wartości liczbowej, bo nie jest wykonalne dzielenie przez zero. Możemy też powiedzieć, że dla $x = 10$ wyrażenie $\frac{8}{x - 10}$ nie ma sensu.

Przykład 3

Zapiszemy w prostszej postaci każde z podanych wyrażeń.
Wyrażenie algebraiczne	Komentarz	Najprostsza postać wyrażenia
$6 \cdot x \cdot y^{2}$	Pomijamy znaki mnożenia.	$6 x y^{2}$
$10 \cdot b \cdot c \cdot a$	Pomijamy znaki mnożenia, litery zapisujemy w porządku alfabetycznym.	$10 a b c$
$0, 5 \cdot w^{3} \cdot z \cdot 4$	Mnożymy liczby, pomijamy znaki mnożenia.	$2 w^{3} z$
$[10 (a - b)] : 2$	Zapisujemy za pomocą kreski ułamkowej i skracamy.	$\frac{10 (a - b)}{2} = 5 (a - b)$
$\frac{2 - a}{2 - a}$	Wyrażenie ma sens dla $a \neq 2$ (mianownik jest wtedy różny od zera). Skracamy ułamek.	$1$

Ważne!

W wyrażeniu algebraicznymwyrażenie algebraicznewyrażeniu algebraicznym nie pomijamy znaku mnożenia, jeżeli litera występuje przed liczbą. Na przykład w wyrażeniach: $a \cdot 8$ , $x \cdot y \cdot 4 \cdot a$ , $(x \cdot 70 - 5) \cdot 2$ .

Zapamiętaj!

Jednomian jest uporządkowany, jeżeli jego pierwszym czynnikiem jest liczba, a następnymi litery w kolejności alfabetycznej.

Za pomocą wyrażeń algebraicznychwyrażenie algebraicznewyrażeń algebraicznych zapisujemy różne wzory, twierdzenia, zwroty matematyczne.

Przykład 4

Oznaczmy przez $x$ pewną liczbę różną od zera. Zapiszemy w postaci wyrażeń algebraicznych podane zwroty.

Liczba o $1$ większa od $x$ :

x + 1

Liczba o $1$ mniejsza od $x$ :

x - 1

Liczba dwukrotnie większa od $x$ :

2 x

Liczba dwukrotnie mniejsza od $x$ :

\frac{x}{2}

Liczba przeciwna do $x$ :

(- x)

Odwrotność liczby $x$ :

\frac{1}{x}

Kwadrat liczby $x$ :

x^{2}

Przykład 5

Zapiszemy w postaci wyrażeń algebraicznych podane zwroty.
Zwrot	Zapis symboliczny
Podwojony iloczyn liczb $a$ , $b$ , $c$ .	$2 a b c$
Iloraz liczb $c$ i $8$ .	$\frac{c}{8}$
Suma liczby $10$ i kwadratu różnicy liczb $x$ i $y$ .	$10 + {(x - y)}^{2}$
Sześcian iloczynu liczb $a$ i $b$ .	${(a b)}^{3}$

Wyrażenia algebraicznewyrażenie algebraiczneWyrażenia algebraiczne można opisać słownie. Wyrażenia mają swoje nazwy. Na przykład $x + 5 y$ to suma algebraiczna, $3 \cdot (a - b)$ to iloczyn. Nazwa wyrażenia algebraicznegowyrażenie algebraicznewyrażenia algebraicznego określa to działanie, które zapisujemy jako ostatnie.

Przykład 6

Zapiszemy słowami każde z podanych wyrażeń.
Wyrażenie zapisane symbolami	Nazwa wyrażenia	Wyrażenie zapisane słowami
$x + 100$	suma	suma liczb $x$ i $100$
$y - 2 x$	różnica	różnica liczby $y$ i podwojonej liczby $x$
$3 (a + 7)$	iloczyn	iloczyn liczby $3$ i sumy liczb $a$ i $7$
$a^{2} + b^{2}$	suma	suma kwadratów liczb $a$ i $b$
$\frac{x + y}{x - y}$	iloraz	iloraz sumy liczb $x$ i $y$ przez różnicę tych liczb

Wyrażenia algebraicznewyrażenie algebraiczneWyrażenia algebraiczne wykorzystujemy do zapisania informacji osadzonych w kontekście praktycznym.

Przykład 7

Zapiszemy odpowiedzi na pytania za pomocą wyrażeń algebraicznych.
Pytanie	Wyrażenie algebraiczne
Ewa ma $a$ lat. Ile lat będzie miała za dwa lata?	$a + 2$
Zenon ma $b$ lat. Ile lat miał $5$ lat temu?	$b - 5$
Bilet normalny kosztuje $x zł$ , a ulgowy $y zł$ . Ile zapłacimy za dwa bilety normalne i cztery ulgowe?	$(2 x + 4 y) zł$
Zeszyt kosztuje $a zł$ , a notes jest o $3 zł$ droższy. Ile kosztują cztery notesy?	$4 (a + 3) zł$
Podstawa trójkąta równoramiennego ma długość $x$ , a ramię ma długość $y$ . Ile jest równy obwód tego trójkąta?	$x + 2 y$

Zależności przedstawione w zadaniach można zapisywać w postaci wyrażeń algebraicznychwyrażenie algebraicznewyrażeń algebraicznych jednej lub kilku zmiennychzmiennezmiennych.

Przykład 8

W dzbanku było $x$ litrów wody, a w butelce $y$ litrów syropu malinowego. Z butelki przelano do dzbanka $0, 5$ litra syropu, otrzymując napój malinowy. Monika odlała z dzbanka $0, 2 l$ napoju dla mamy, a resztę przelała do $6$ szklanek, napełniając każdą z nich całkowicie.
Ile jest teraz napoju w dzbanku? Ile jest teraz syropu w butelce? Jaka była pojemność szklanki?

Treść zadania zapiszemy w tabelce.
Zawartość	dzbanka (w $l$ )	butelki (w $l$ )	jednej szklanki (w $l$ )
początkowa	$x$	$y$	$-$
po przelaniu syropu do dzbanka	$x + 0, 5$	$y - 0, 5$	$-$
po odlaniu napoju dla mamy	$x + 0, 5 - 0, 2$	$y - 0, 5$	$-$
po rozlaniu do szklanek	$0$	$y - 0, 5$	$\frac{x + 0, 5 - 0, 2}{6}$

Otrzymane wyrażenie opisujące pojemność szklanki, możemy zapisać w prostszej postaci:
$\frac{x + 0, 5 - 0, 2}{6} = \frac{x + 0, 3}{6}$ .

Odpowiedź:
W dzbanku nie ma już napoju, w butelce jest $y - 0, 5$ litra syropu, pojemność jednej szklanki jest równa $\frac{x + 0, 3}{6}$ .

Notatki

RzIv7kbNQwBK2

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Prezentacja multimedialna

Polecenie 1

Zapoznaj się z prezentacją pokazującą przykłady tworzenia wyrażeń algebraicznychwyrażenie algebraicznewyrażeń algebraicznych opisujących zależności występujące w treści zadania. Zwróć uwagę na różne sposoby zapisywania obliczeń.

RsMgRWWyzCinc

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Transkrypcjaazurewhite

R4itwFTDu2D1D

ReyyO18XdgRt1

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Transkrypcjaazurewhite

RJ3SDLASDglZp

Transkrypcjaazurewhite

Zajmiemy się teraz zadaniami, w których niektóre wielkości oznaczone są literami, a niektóre liczbami.

Przykład drugi
Do pustej windy na parterze budynku czteropiętrowego wsiadło $n$ osób. Wiadomo, że $n$ jest liczbą większą od zera.
Na pierwszym piętrze wysiadła jedna trzecia wszystkich osób i nikt nie wsiadł.
Na drugim piętrze nikt nie wysiadł, ale wsiadło dwa razy tyle osób, co wysiadło na pierwszym piętrze.
Na trzecim piętrze jedna osoba wsiadła i trzy wysiadły.
Na czwartym piętrze wszyscy wysiedli.
Obliczymy, ile osób wysiadło na czwartym piętrze.

RN7RIib31yPee

R8fk2yM9pWftd

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Transkrypcjaazurewhite

R1AQ5PjgiKM9J

RES4SlIxgp1ba

Na slajdzie jest białe tło. Ramka w kolorze zielonym. Po prawej stronie ekranu jest napis: "Przykład 3". W górnej części ekranu tekst: "Towarzystwo składające się z "a" osób wybrało się na wycieczkę furmankami. Każda furmanka zabierała siedem osób (nie licząc furmana). Niestety zabrakło miejsca dla "b" osób. Ustalimy, ile było furmanek." Poniżej znajduje się fotografia przedstawiająca furmankę prowadzoną przez dwa konie. Na furmance siedzi kilka osób. — Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Transkrypcjaazurewhite

Przykład trzeci
Towarzystwo składające się z $a$ osób wybrało się na wycieczkę furmankami. Każda furmanka zabierała siedem osób (nie licząc furmana). Niestety zabrakło miejsc dla $b$ osób.

RxlTnNQtnJMbG

R1dSVg9CQUNN3

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Transkrypcjaazurewhite

Rn3SXPJKWLQwV

R14MyHfaiX06t

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Transkrypcjaazurewhite

Przykład czwarty
Wojtek miał $x$ złotych. Basi dał trzydzieści złotych i teraz Basia ma $5$ razy więcej pieniędzy niż Wojtek. Obliczymy, ile pieniędzy miała Basia początkowo.

Możemy to zadanie rozwiązać, korzystając z tabelki – tak, jak w Przykładzie drugim.
Możemy też przeprowadzić odpowiednie rozumowanie.

R1NetHIpuM4aJ

RGUgIMwUbXVeG

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Transkrypcjaazurewhite

Przykład piąty
Zmieszano dwa kilogramy cukierków czekoladowych po $x$ złotych za kilogram, pięć kilogramów cukierków jagodowych po $y$ złotych za kilogram i trzy kilogramy cukierków miodowych po $w$ złotych za kilogram.
Obliczymy, ile powinien kosztować kilogram takiej mieszanki.
Rozwiązanie zawrzemy w kilku krokach.

Rb8PUJb2OIR3z

Transkrypcjaazurewhite

Przykład szósty
Z miejscowości $A$ i $B$ odległych od siebie o $s$ kilometrów wyruszyli naprzeciw siebie dwaj wędrowcy - Jarek i Darek.
Jarek pokonuje $a$ kilometrów dziennie, a Darek o $b$ kilometrów więcej.

Rks7Khuikts0n

R1ErGc9bFJkUh

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Transkrypcjaazurewhite

Slajd pierwszy:

Nagranie ukazuje zbliżenie na rękę osoby piszącej po tablicy szkolnej. W tle widoczna ręka drugiej osoby, która także notuje na tablicy. W prawym górnym rogu znajduje się tekst: „Wyrażenia algebraiczne”. Tekst jest biały, na zielonym tle.

Slajd drugi:

Przykład pierwszy.

Zapiszemy za pomocą wyrażenia algebraicznego dowolną liczbę naturalną trzycyfrową. Skorzystamy z tego, że każdą liczbę naturalną w dziesiątkowym układzie pozycyjnym można zapisać w postaci sumy. Na przykład sześćset dwadzieścia siedem to suma sześciu setek, dwóch dziesiątek, siedmiu jedności.

Chcąc zapisać dowolną liczbę trzycyfrową za pomocą wyrażenia algebraicznego, oznaczmy najpierw przez a cyfrę setek tej liczby, przez b, cyfrę dziesiątek i przez c cyfrę jedności. Przy czym cyfrą setek nie może być zerem.

Zapisujemy liczbę trzycyfrową w postaci sumy, czyli $a \cdot 100 + 10 \cdot b + c \cdot 1 = 100 \cdot a + 10 \cdot b + c = 100 a + 10 b + c$ . Podczas obliczeń korzystamy z przemienności mnożenia, a następnie pomijamy znak mnożenia. Dowolna liczba trzycyfrowa: $100 a + 10 b + c$ , gdzie $a$ to $1, 2, 3, 4, 5, 6, 7, 8$ lub $9$ , $b$ to $0, 1, 2, 3, 4, 5, 6, 7, 8$ lub $9$ , $c$ to $0, 1, 2, 3, 4, 5, 6, 7, 8$ lub $9$ .

Slajd trzeci:

Przykład drugi.

Do pustej windy na parterze budynku czteropiętrowego wsiadło n osób. Wiadomo, że en jest liczbą większą od zera. Na pierwszym piętrze wysiadła jedna trzecia wszystkich osób i nikt nie wsiadł. Na drugim piętrze nikt nie wysiadł, ale wsiadło dwa razy tyle osób, co wysiadło na pierwszym piętrze. Na trzecim piętrze jedna osoba wsiadła i trzy wysiadły. Na czwartym piętrze wszyscy wysiedli. Obliczymy, ile osób wysiadło na czwartym piętrze.

Slajd czwarty:

Treść zadania jest dość długa, zatem dla ułatwienia, kolejne liczby osób znajdujących się w windzie, zapiszemy w tabelce. Liczbę osób, które wsiadły poprzedzimy znakiem plus, a które wysiadły – znakiem minus. Oto tabela.

Poziom budynku	Liczba osób która wsiadła/wysiadła	Liczba osób w windzie
parter	plus en	en
Pierwsze piętro	minus $\frac{1}{3} n$	$\frac{2}{3} n$
Drugie piętro	plus $\frac{2}{3} n$	$\frac{4}{3} n$
Trzecie piętro	plus jeden przecinek minus trzy	$\frac{4}{3} n - 2$
Czwarte piętro	$- (\frac{4}{3} n - 2)$	zero

Na parterze do windy wsiadło $n$ osób. Na pierwszym piętrze wysiadła jedna trzecia wszystkich osób. W windzie zostało więc dwie trzecie osób, które wsiadły na parterze. Na drugim piętrze nikt nie wysiadł, ale wsiadło dwa razy tyle osób, co wysiadło na pierwszym piętrze, zatem dwie trzecie en. W windzie jest więc teraz cztery trzecie en osób. Na trzecim piętrze jedna osoba wsiadła i trzy wysiadły. W konsekwencji w windzie jest teraz o dwie osoby mniej. Do czwartego piętra dojechało cztery trzecie en minus dwie osoby i wszystkie te osoby wysiadły na tym piętrze.

Odpowiedź:
Na czwartym piętrze wysiadły $\frac{4}{3} n - 2$ osoby.

Slajd piąty:

Przykład trzeci.

Towarzystwo składające się z $a$ osób wybrało się na wycieczkę furmankami. Każda furmanka zabierała siedem osób (nie licząc furmana). Niestety zabrakło miejsc dla $b$ osób. Ustalimy, ile było furmanek.

Slajd szósty:

Furmanki miały zabrać $a$ osób, ponieważ dla $b$ osób zabrakło miejsca, to furmanki zabrały tylko $a$ minus $b$ osób. Zauważmy przy tym, że liczba $a$ musi być większa od liczby $b$ . Jedna furmanka zaierała siedem osób. Zatem, aby ustalić ile było furmanek, należy podzielić liczbę wszystkich zabranych osób przez liczbę osób, które zabierała jedna furmanka. Zatem mamy $\frac{a - b}{7}$ .

Odpowiedź:
Było $\frac{a - b}{7}$ furmanek.

Slajd siódmy:

Przykład czwarty.

Wojtek miał $x$ złotych. Basi dał trzydzieści złotych i teraz Basia ma pięć razy więcej pieniędzy niż Wojtek. Obliczymy, ile pieniędzy miała Basia początkowo. Możemy to zadanie rozwiązać, korzystając z tabelki – tak, jak w Przykładzie drugim. Możemy też przeprowadzić odpowiednie rozumowanie.

Slajd ósmy:

Jeśli bowiem Wojtek miał początkowo iks złotych, Basi dał trzydzieści złotych, to teraz ma o trzydzieści złotych mniej, czyli $(x - 30) zł$ . Zauważmy, że liczba iks minus trzydzieści musi być dodatnia. Wynika z tego, że początkowa kwota, jaką dysponował Wojtek, musiała być większa niż trzydzieści złotych, czyli $x > 30$ . Basia ma teraz pięć razy tyle ile teraz ma Wojtek, czyli $5 (x - 30) zł$ . Od kwoty, którą teraz ma Basia, trzeba odjąć trzydzieści złotych, które dostała od Wojtka i otrzymamy kwotę, którą miała początkowo, czyli $[5 (x - 30) - 30] z ł$ .

Odpowiedź:
Basia miała początkowo $[5 (x - 30) - 30] z ł$ .

Slajd dziewiąty:

Przykład piąty.

Zmieszano dwa kilogramy cukierków czekoladowych po $x$ złotych za kilogram, pięć kilogramów cukierków jagodowych po $y$ złotych za kilogram i trzy kilogramy cukierków miodowych po w złotych za kilogram. Obliczymy, ile powinien kosztować kilogram takiej mieszanki. Rozwiązanie zawrzemy w kilku krokach. Najpierw opisujemy za pomocą wyrażenia algebraicznego koszt dwóch kilogramów cukierków czekoladowych po iks złotych za kilogram, czyli $2 x$ . Teraz opisujemy koszt pięciu kilogramów cukierków jagodowych po igrek złotych za kilogram, czyli $5 y$ . Wreszcie opisujemy koszt trzech kilogramów cukierków miodowych po w złotych za kilogram, czyli $3 w$ . Dodajemy wszystkie zapisane wcześniej wyrażenia i otrzymujemy wartość mieszanki złożonej z trzech rodzajów cukierków, czyli $(2 x + 5 y + 3 w) zł$ . Masa mieszanki jest równa dziesięć kilogramów, ponieważ zmieszano dwa kilogramy cukierków czekoladowych, pięć kilogramów cukierków jagodowych i trzy kilogramy cukierków miodowych. Aby obliczyć, jaka powinna być cena kilograma mieszanki, trzeba podzielić koszt mieszanki przez jej masę. Zatem $\frac{2 x + 5 y + 3 w}{10}$ .

Odpowiedź:
Cena kilograma mieszanki powinna być równa $\frac{2 x + 5 y + 3 w}{10}$ .

Slajd dziesiąty:

Przykład szósty.

Z miejscowości A i B odległych od siebie o $s$ kilometrów wyruszyli naprzeciw siebie dwaj wędrowcy - Jarek i Darek. Jarek pokonuje $a$ kilometrów dziennie, a Darek o $b$ kilometrów więcej. Odpowiemy na pytanie – po ilu dniach Jarek i Darek spotkają się?

Slajd jedenasty:

Zilustrujemy treść zadania na rysunku. Na slajdzie narysowano odcinek na każdym końcu odcinka narysowano chłopca. Podpisano odcinek jako $s$ kilometrów. Od chłopca po lewej stronie zaznaczono odcinek o długości $a$ kilometrów. Od chłopa po prawej stronie narysowano odcinek długości $a$ plus $b$ kilometrów. Jarek pokonywał dziennie $a$ kilometrów a Darek o $b$ kilometrów więcej, więc $a$ plus $b$ kilometrów. Dziennie wędrowcy pokonywali w sumie dwa $a$ plus $b$ kilometrów. O tyle też kilometrów zbliżali się dziennie do siebie. Aby obliczyć po ilu dniach Jarek i Darek spotkają się, należy długość drogi z A do B podzielić przez długość drogi pokonywanej w sumie dziennie przez wędrowców. Zauważmy przy tym, że obie liczby $a$ i $b$ są dodatnie, zatem dzielenie jest wykonalne. Wyrażenie jest postaci $\frac{s}{2 a + b}$ .

Odpowiedź:
Jarek i Darek spotkają się po $\frac{s}{2 a + b}$ dniach.

Polecenie 2

Wzorując się na Przykładzie $1$ podanym w prezentacji, zapisz dowolną liczbę naturalną czterocyfrową za pomocą wyrażenia algebraicznegowyrażenie algebraicznewyrażenia algebraicznego.

R4ybku0gduiZF

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Każdą liczbę naturalną czterocyfrową w dziesiątkowym układzie pozycyjnym, można zapisać za pomocą sumy. Na przykład:
$1234 = 1 \cdot 1000 + 2 \cdot 100 + 3 \cdot 10 + 4 \cdot 1$ .

Oznaczmy:
$a$ – cyfra tysięcy liczby czterocyfrowej równa $1$ , $2$ , $3$ , $4$ , $5$ , $6$ , $7$ , $8$ lub $9$ ,
$b$ – cyfra setek liczby czterocyfrowej równa $0$ , $1$ , $2$ , $3$ , $4$ , $5$ , $6$ , $7$ , $8$ lub $9$ ,
$c$ – cyfra dziesiątek liczby czterocyfrowej równa $0$ , $1$ , $2$ , $3$ , $4$ , $5$ , $6$ , $7$ , $8$ lub $9$ ,
$d$ – cyfra jedności liczby czterocyfrowej równa $0$ , $1$ , $2$ , $3$ , $4$ , $5$ , $6$ , $7$ , $8$ lub $9$ .
Dowolną liczbę naturalną czterocyfrową możemy wtedy zapisać w postaci:

1000 a + 100 b + 10 c + d

Polecenie 3

Korzystając z danych zawartych w Przykładzie $2$ prezentacji, określ najmniejszą liczbę osób, które mogły wsiąść na parterze do windy oraz najmniejszą liczbę osób, które mogły wysiąść na $IV$ piętrze.

R1SBw4DAPHkRf

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Liczba osób to liczba naturalna dodatnia. Aby liczby $\frac{1}{3} n$ i $\frac{2}{3} n$ były również liczbami naturalnymi, liczba $n$ musi być dodatnią wielokrotnością liczby $3$ . Najmniejsza z takich wielokrotności to $3$ . Zatem na parterze wsiadły co najmniej trzy osoby.
Zatem na czwartym piętrze mogły wysiąść co najmniej
$\frac{4}{3} \cdot 3 - 2 = 4 - 2 = 2$ osoby.

Polecenie 4

Wykaż, że suma trzech kolejnych liczb naturalnych dodatnich jest podzielna przez $3$ .

R1Rt47kxB9cV2

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

$n, n + 1, n + 2$ - trzy kolejne liczby naturalne.

$n, n + 1, n + 2$ - trzy kolejne liczby naturalne, gdzie $n$ jest liczbą naturalną dodatnią. Zapisujemy i przekształcamy sumę tych liczb:

$n + n + 1 + n + 2 = 3 n + 3 = 3 (n + 1)$ .

Otrzymana suma jest równa iloczynowi liczby $3$ i liczby naturalnej $n + 1$ , co oznacza, że jest podzielna przez $3$ .

Zestaw ćwiczeń interaktywnych

Rzz4FfgYu53rp

Ćwiczenie 1

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

R2m0bGRIJxIqT

Ćwiczenie 2

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

RhnPjdCx9GMpC

Ćwiczenie 3

Połącz w pary każde wyrażenie zapisane słowami i to samo wyrażenie zapisane symbolami. Sześcian liczby

a

. Możliwe odpowiedzi: 1.

a + 3

, 2.

a^{3}

, 3.

\frac{a}{3}

, 4.

3 a - 3

, 5.

a^{3} + 3

, 6.

3 - a

, 7.

3 a

Liczba trzy razy większa od

a

. Możliwe odpowiedzi: 1.

a + 3

, 2.

a^{3}

, 3.

\frac{a}{3}

, 4.

3 a - 3

, 5.

a^{3} + 3

, 6.

3 - a

, 7.

3 a

Liczba trzy razy mniejsza od

a

. Możliwe odpowiedzi: 1.

a + 3

, 2.

a^{3}

, 3.

\frac{a}{3}

, 4.

3 a - 3

, 5.

a^{3} + 3

, 6.

3 - a

, 7.

3 a

Liczba o trzy większa od

a

. Możliwe odpowiedzi: 1.

a + 3

, 2.

a^{3}

, 3.

\frac{a}{3}

, 4.

3 a - 3

, 5.

a^{3} + 3

, 6.

3 - a

, 7.

3 a

Liczba o

a

mniejsza od trzech. Możliwe odpowiedzi: 1.

a + 3

, 2.

a^{3}

, 3.

\frac{a}{3}

, 4.

3 a - 3

, 5.

a^{3} + 3

, 6.

3 - a

, 7.

3 a

Liczba o trzy większa od sześcianu liczby

a

. Możliwe odpowiedzi: 1.

a + 3

, 2.

a^{3}

, 3.

\frac{a}{3}

, 4.

3 a - 3

, 5.

a^{3} + 3

, 6.

3 - a

, 7.

3 a

Liczba o

3

mniejsza od potrojonej liczby

a

. Możliwe odpowiedzi: 1.

a + 3

, 2.

a^{3}

, 3.

\frac{a}{3}

, 4.

3 a - 3

, 5.

a^{3} + 3

, 6.

3 - a

, 7.

3 a

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Ćwiczenie 4

RUoIH6VAjN8CR

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

RbkyWuqHK8ZoI

Ćwiczenie 5

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Ćwiczenie 6

R12EqtSYiMUxs

Uzupełnij zdania, wpisując odpowiednie liczby. W sklepie są jabłka w cenie

2 zł

, gruszki w cenie

6 zł

i banany w cenie

4 zł

.
Arek kupił (6) kilogramów jabłek oraz

x

kilogramów gruszek i zapłacił

6 (x + 2)

złotych.
Bolek kupił

x

kilogramów bananów oraz Tu uzupełnij razy więcej jabłek i zapłacił

8 x

złotych.
Celina kupiła pół kilograma bananów,

x

kilogramów jabłek oraz Tu uzupełnij kilogramy gruszek i zapłaciła

2 x + 20

złotych.

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Zauważ, że cena $x$ kilogramów jabłek wynosi $2 x zł$ , cena $x$ kilogramów gruszek wynosi $6 x zł$ , a cena $x$ kilogramów bananów wynosi $4 x zł$ .

Skoro Arek zapłacił $6 (x + 2) = 6 x + 12$ złotych i kupił $x$ kilogramów gruszek, to za gruszki zapłacił $6 x$ złotych, zatem cena jabłek wynosiła $12$ złotych, czyli kupił $\frac{12}{2} = 6$ kilogramów jabłek.
Skoro Bolek zapłacił $8 x$ złotych i kupił $x$ kilogramów bananów, to za banany zapłacił $4 x$ złotych, zatem cena jabłek wynosiła $4 x$ złotych, czyli kupił $2$ razy więcej jabłek niż bananów.
Skoro Celina zapłaciła $2 x + 20$ złotych i kupiła pół kilograma bananów oraz $x$ kilogramów jabłek, to za banany i jabłka zapłaciła $2 x + 2$ złotych, zatem cena gruszek wynosiła $18$ złotych, czyli kupiła $\frac{18}{6} = 3$ kilogramy gruszek.

Ćwiczenie 7

Zapisz w postaci wyrażenia algebraicznego każde z podanych twierdzeń.

Podwojona suma liczb $x$ i $3 y$ .
Iloraz sumy liczb $x$ i $y$ przez kwadrat liczby $y$ .
Kwadrat różnicy liczby $y$ i $x$ .
Iloczyn liczby o $4$ większej od $x$ przez $y$ .
Różnica kwadratu liczby $y$ i liczby $3 x$ .

RKKtqF3HU87cD

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Suma to wynik dodawania.
Iloraz to wynik dzielenia.
Różnica to wynik odejmowania.
Iloczyn to wynik mnożenia.
Kwadrat liczby $y$ to $y^{2}$ .

$2 (x + 3 y)$
$\frac{x + y}{y^{2}}$
${(y - x)}^{2}$
$(x + 4) \cdot y$
$y^{2} - 3 x$

Ćwiczenie 8

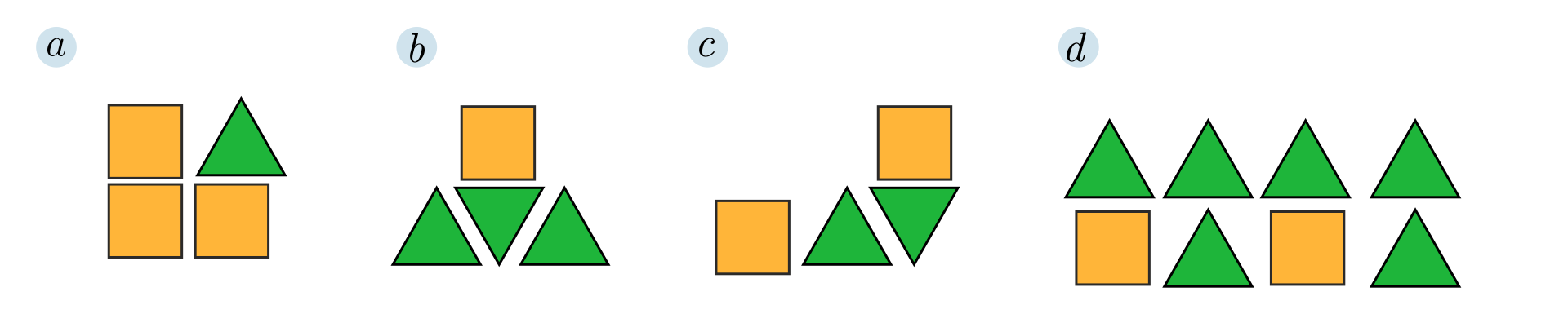
Pole kwadratu jest równe $a$ . Pole trójkąta jest równe $1 + b$ . Opisz wyrażeniem algebraicznym pole każdej z figur.

R1VZ2BGN2dLVa

Grafika podzielona jest na cztery części oznaczone literami: "a", "b", "c", "d". Na ilustracji oznaczonej literą "a", ukazane są trzy pomarańczowe kwadraty oraz jeden zielony trójkąt równoboczny. Na ilustracji oznaczonej literą "b", ukazane są trzy zielone trójkąty równoboczne oraz jeden pomarańczowy kwadrat. Na ilustracji oznaczonej literą "c", ukazane są dwa pomarańczowe kwadraty oraz dwa zielone trójkąty równoboczne. Na ilustracji oznaczonej literą "d", ukazane są dwa pomarańczowe kwadraty oraz sześć zielonych trójkątów równobocznych. — Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Rnq1tIelE8KtF

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Figura składa się z trzech kwadratów – każdy o polu $a$ i trójkąta o polu $1 + b$ .
Figura składa się z kwadratu o polu $a$ i trzech trójkątów o polu $1 + b$ każdy.
Figura składa się z dwóch kwadratów – każdy o polu $a$ i dwóch trójkątów – każdy o polu $1 + b$ .
Figura składa się z dwóch kwadratów – każdy o polu $a$ i sześciu trójkątów – każdy o polu $1 + b$ .

$P = a + a + a + 1 + b = 3 a + b + 1$ .
$P = a + 1 + b + 1 + b + 1 + b = a + 3 b + 3$ .
$P = a + a + 1 + b + 1 + b = 2 a + 2 b + 2$ .
$P = a + a + 1 + b + 1 + b + 1 + b + 1 + b + 1 + b + 1 + b = 2 a + 6 b + 6$ .

Słownik

wyrażenie algebraiczne

wyrażenie zbudowane z liczb, liter, znaków działań, nawiasów.

zmienne

litery występujące w wyrażeniach algebraicznych.

Bibliografia

Gonick L., (2016), Algebra w obrazkach, Warszawa: Prószyński i S‑ka.