Układ dwóch równań liniowych
Ten materiał poświęcony jest przykładom związanym z układami dwóch równań liniowych. Jeżeli chcesz sobie przypomnieć podstawowe wiadomości na temat układów równań zajrzyj do materiału Układ równań liniowychUkład równań liniowych. Zdobytą wiedzę sprawdzisz rozwiązując ćwiczenia zawarte w materiale Układ dwóch równań liniowych - zadaniaUkład dwóch równań liniowych - zadania.
Analizując wykresy dwóch funkcji liniowych, zaznaczonych w tym samym układzie współrzędnych, możemy stwierdzić, czy wykresy te mają punkty wspólne.
Rysunek przedstawia wykresy funkcji i .
Z rysunku odczytamy, że wykresy funkcji przecinają się w punkcie .

Obliczając wartość każdej z funkcji dla argumentu , stwierdzamy, że
a także
Wykresy funkcji i nie są prostymi równoległymi. Punkt jest ich jedynym punktem wspólnym.
Nie zawsze jednak można z rysunku dokładnie odczytać współrzędne punktu przecięcia wykresów dwóch funkcji liniowych.
Jest to trudne np. w przypadku wykresów funkcji i .

Rozwiążemy układ równań
sposób
Wyznaczymy z drugiego równania niewiadomą
Następnie wykorzystujemy otrzymany związek w pierwszym równaniu, skąd otrzymujemy
Wobec tego
Rozwiązaniem danego układu jest więc para liczb oraz .
sposób
Rozwiążemy dany układ metodą graficzną.
Wyznaczymy z każdego równania układu
Proste o równaniach i nie są równoległe, więc przecinają się w jednym punkcie.
Rysunek przedstawia obie te proste w układzie współrzędnych.

Odczytujemy z rysunku, że te proste przecinają się w punkcie .
Wobec tego układ równań
ma jedno rozwiązanie, parę liczb oraz .
Rozwiążemy układ równań
sposób
Z drugiego równania natychmiast wynika, że . Po wstawieniu otrzymanej wartości do pierwszego równania otrzymujemy , skąd .
Para i jest więc jedynym rozwiązaniem danego układu.
sposób
Rozwiążemy dany układ metodą graficzną.
Z pierwszego równania wyznaczamy , ale w drugim równaniu ta niewiadoma nie występuje.
Zapisujemy więc drugie równanie w postaci
Zauważmy, że równanie opisuje zbiór wszystkich takich punktów, których pierwsza współrzędna jest równa .
Jest to więc równanie prostej równoległej do osi , przecinającej oś w punkcie .
Rysunek przedstawia proste o równaniach i w układzie współrzędnych.

Odczytujemy z niego, że te proste przecinają się w punkcie .
Oznacza to, że układ równań
ma jedno rozwiązanie, parę liczb oraz .
Para i jest rozwiązaniem układu równań ,
ponieważ dla i jest
oraz
Nie jest to jedyne rozwiązanie tego układu, co stwierdzimy, wyznaczając z każdego z równań układu
Oba równania opisują tę samą prostą, a zatem układ ten ma nieskończenie wiele rozwiązań. Jest nim każda para liczb rzeczywistych i , która spełnia równanie .
Rysunek przedstawia prostą o równaniu .

Pokażemy, że układ
nie ma rozwiązań.
Wyznaczamy z każdego z równań układu
Proste o równaniach i są równoległe i różne, więc dany układ nie ma rozwiązań.
Rysunek przedstawia obie te proste w układzie współrzędnych.

Film dostępny pod adresem /preview/resource/R1R24SM9WD8Ja
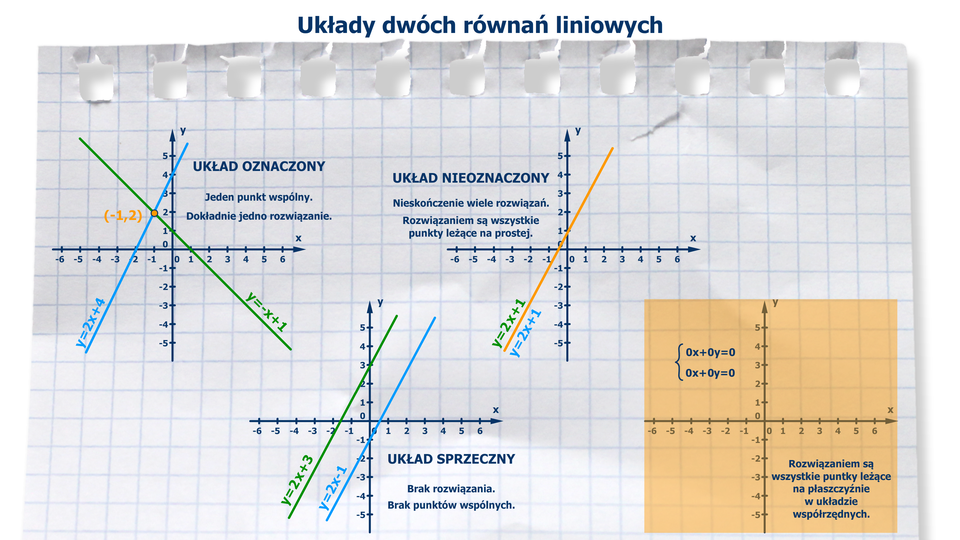
Animacja pokazuje interpretację geometryczną czterech różnych układów równań liniowych.