Wartość najmniejsza oraz wartość największa funkcji kwadratowej w przedziale domkniętym
W tym materiale zawarte są wiadomości na temat funkcji kwadratowej określonej na zbiorze domkniętym. Dowiesz się w jaki sposób wyznaczyć wartość najmniejszą oraz wartość największą tego rodzaju funkcji oraz jak określić na których przedziałach funkcja kwadratowa jest rosnąca, a na których jest ona malejąca.
Obliczymy wartość najmniejszą oraz wartość największą funkcji kwadratowej w każdym z podanych przedziałów:
,
,
.
Ustalmy własności funkcji , gdy jest ona określona dla każdej liczby rzeczywistej.
Ponieważ współczynnik przy we wzorze funkcji jest dodatni, więc wykresem tej funkcji jest parabola o ramionach skierowanych do góry. Wierzchołek tej paraboli ma współrzędne
Zatem najmniejszą wartością funkcji jest
Najmniejszą wartość funkcji można też obliczyć, korzystając ze wzoru na drugą współrzędną wierzchołka paraboli
Zauważmy, że
maksymalnym przedziałem, w którym funkcja jest malejąca, jest ,
maksymalnym przedziałem, w którym funkcja jest rosnąca, jest .
R1DnMdIzWpw881 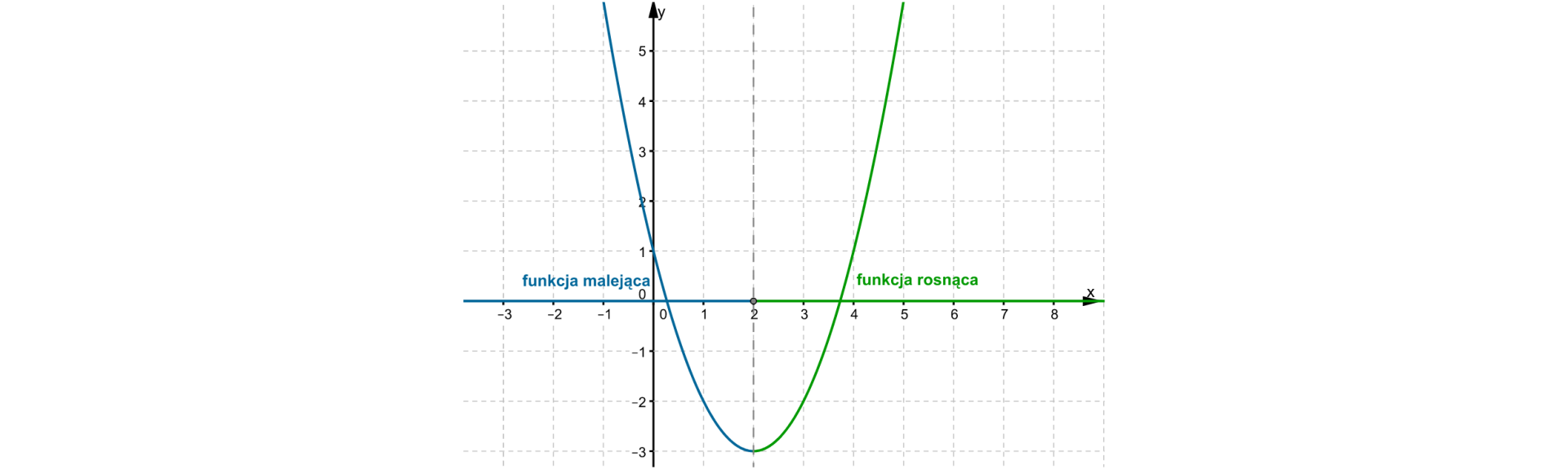 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Przedział jest zawarty w przedziale , więc funkcja jest w tym przedziale malejąca.
Oznacza to, żenajwiększą wartością funkcji w przedziale jest wartość w lewym krańcu tego przedziału, czyli ,
najmniejszą wartością funkcji w przedziale jest wartość w prawym krańcu tego przedziału, czyli .
Pierwsza współrzędna wierzchołka paraboli należy do przedziału , więc najmniejszą wartością funkcji w przedziale jest .
W przedziale funkcja jest malejąca, a w przedziale ta funkcja jest rosnąca. Wobec tego do ustalenia wartości największej funkcji w przedziale wystarczy porównać wartości oraz .
Obliczamy:
, . Oznacza to, że największą wartością funkcji w przedziale jest .Przedział jest zawarty w przedziale , więc funkcja jest w tym przedziale rosnąca.
Wobec tegonajwiększą wartością funkcji w przedziale jest wartość w prawym krańcu tego przedziału, czyli ,
najmniejszą wartością funkcji w przedziale jest wartość w lewym krańcu tego przedziału, czyli .
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/P1Ev29y4I
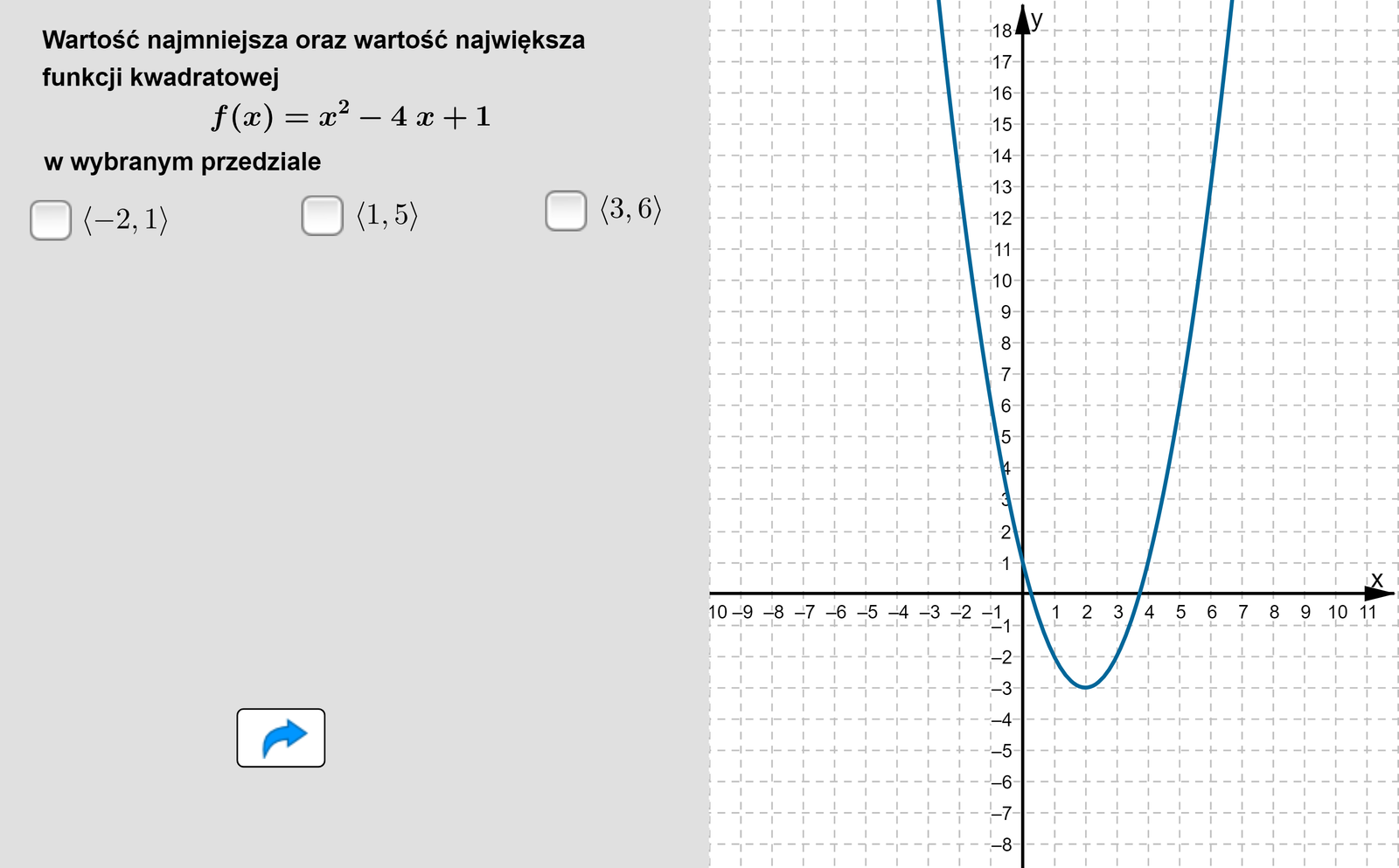
Rozpatrzymy teraz funkcję w wybranych przedziałach.
Przedział . Funkcja jest malejąca w przedziale i rosnąca w przedziale . Zatem funkcja jest malejąca w przedziale , ponieważ jest on zawarty w przedziale . Największą wartością przyjmowaną w rozpatrywanym przedziale jest . Najmniejszą wartością przyjmowaną w rozpatrywanym przedziale jest .
Przedział . Pierwsza współrzędna wierzchołka paraboli należy do rozpatrywanego przedziału, więc najmniejszą wartością funkcji w tym przedziale jest . Obliczmy wartości na końcach przedziału. Otrzymujemy: oraz . Zatem największą wartością funkcji w tym przedziale jest .
Przedział . Funkcja jest w tym w przedziale rosnąca, ponieważ zawiera się on w maksymalnym przedziale, w którym funkcja jest rosnąca. Najmniejsza wartość w tym przedziale jest na jego lewym końcu . Największa wartość w tym przedziale jest na jego prawym końcu .
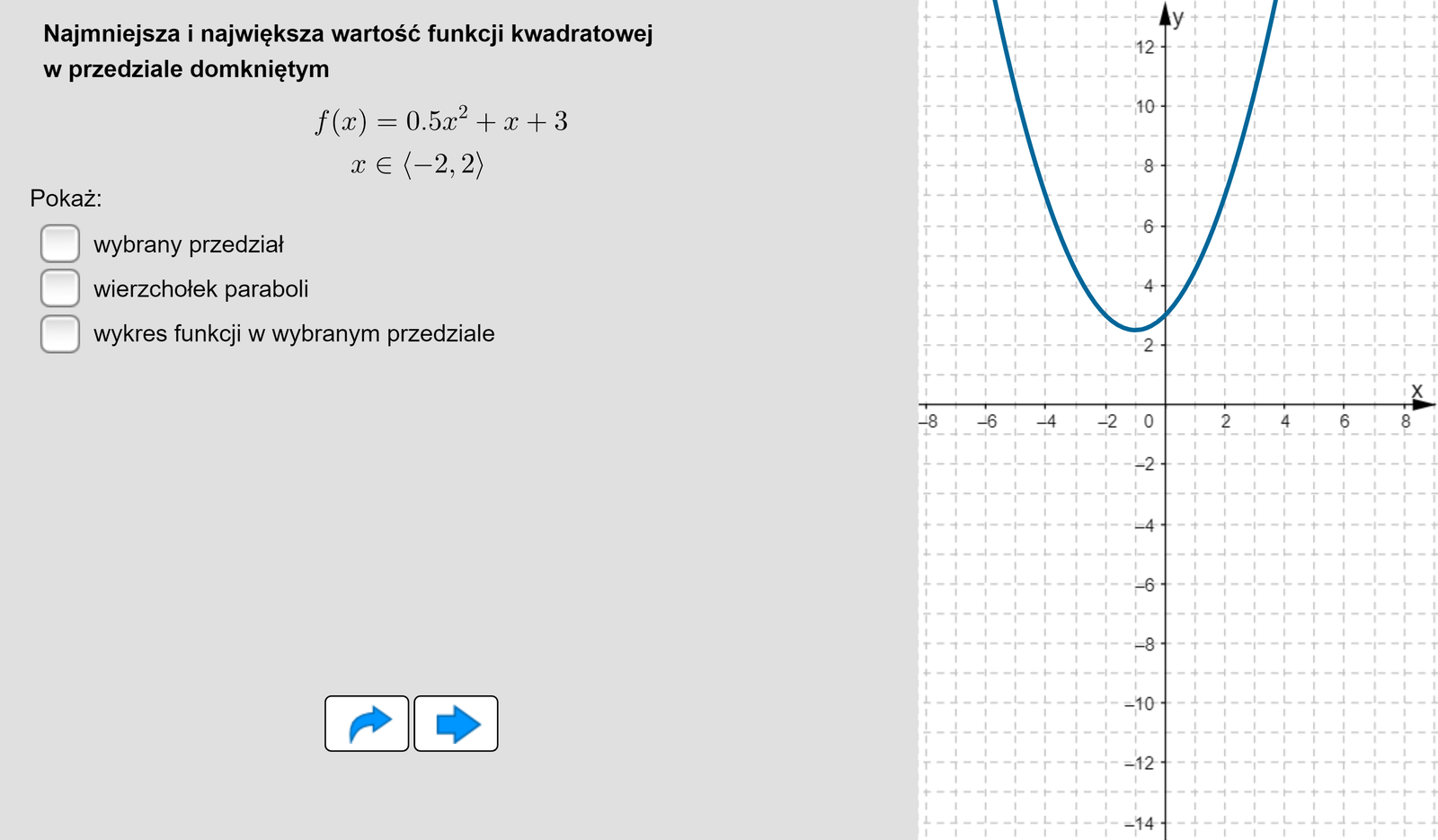
Obliczymy najmniejszą wartość funkcji kwadratowej w przedziale .
Współczynnik przy we wzorze funkcji jest ujemny, zatem wykresem tej funkcji jest parabola o ramionach skierowanych w dół.
Wierzchołek tej paraboli ma współrzędne
Zatem w przedziale funkcja jest rosnąca, a w przedziale funkcja jest malejąca.
Oznacza to, że najmniejszą wartością funkcji jest odpowiednio lub .
Obliczamy:
Najmniejszą wartością funkcji w przedziale jest więc .

Obliczymy największą wartość funkcji kwadratowej w przedziale .
Współczynnik przy we wzorze funkcji jest ujemny, zatem wykresem tej funkcji jest parabola o ramionach skierowanych w dół. Pierwsza współrzędna wierzchołka tej paraboli jest równa

Funkcja ta jest zatem rosnąca w przedziale i malejąca w przedziale . Ponieważ przedział jest zawarty w przedziale , więc funkcja jest w tym przedziale malejąca.
Największą wartość funkcja przyjmuje w lewym krańcu tego przedziału.
Największą wartością funkcji w przedziale jest .
Obliczymy wartość najmniejszą oraz wartość największą funkcji kwadratowej w przedziale .
Przekształcamy wzór funkcji do postaci iloczynowej.
Współczynnik przy we wzorze funkcji jest równy , zatem wykresem tej funkcji jest parabola o ramionach skierowanych w górę.
Miejscami zerowymi funkcji są liczby oraz . Pierwsza współrzędna wierzchołka tej paraboli jest równa
więc należy do przedziału .
Oznacza to, że liczba
jest najmniejszą wartością funkcji w przedziale .
Aby ustalić wartość największą, obliczamy wartości funkcji w obu krańcach danego przedziału
oraz
Wobec tego jest największą wartością funkcji w przedziale .
Funkcja przyporządkowuje każdej liczbie z przedziału różnicę tej liczby i kwadratu liczby o mniejszej od niej. Wyznaczymy wzór funkcji oraz obliczymy jej największą wartość w przedziale .
Z treści zadania wynika, że funkcja określona jest wzorem
Przekształcamy ten wzór
stąd
Jest to więc funkcja kwadratowa, a w jej wzorze współczynnik przy jest ujemny. Wykresem funkcji jest więc parabola o ramionach skierowanych w dół.
Pierwsza współrzędna wierzchołka tej paraboli jest równa
więc liczba nie należy do przedziału .
W przedziale funkcja jest rosnąca, co oznacza, że największą wartością funkcji jest wartość w prawym krańcu tego przedziału, czyli .
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/P1Ev29y4I
Ustalimy, jaki jest możliwie największy iloczyn dwóch liczb, o których wiadomo, że suma pierwszej z nich i podwojonej drugiej jest równa
Oznaczmy przez
Wiadomo, że
Iloczyn
Otrzymaną funkcję kwadratową
Ponieważ współczynnik przy
Pierwsza współrzędna wierzchołka
Oznacza to, że dla
Zauważmy, że gdy
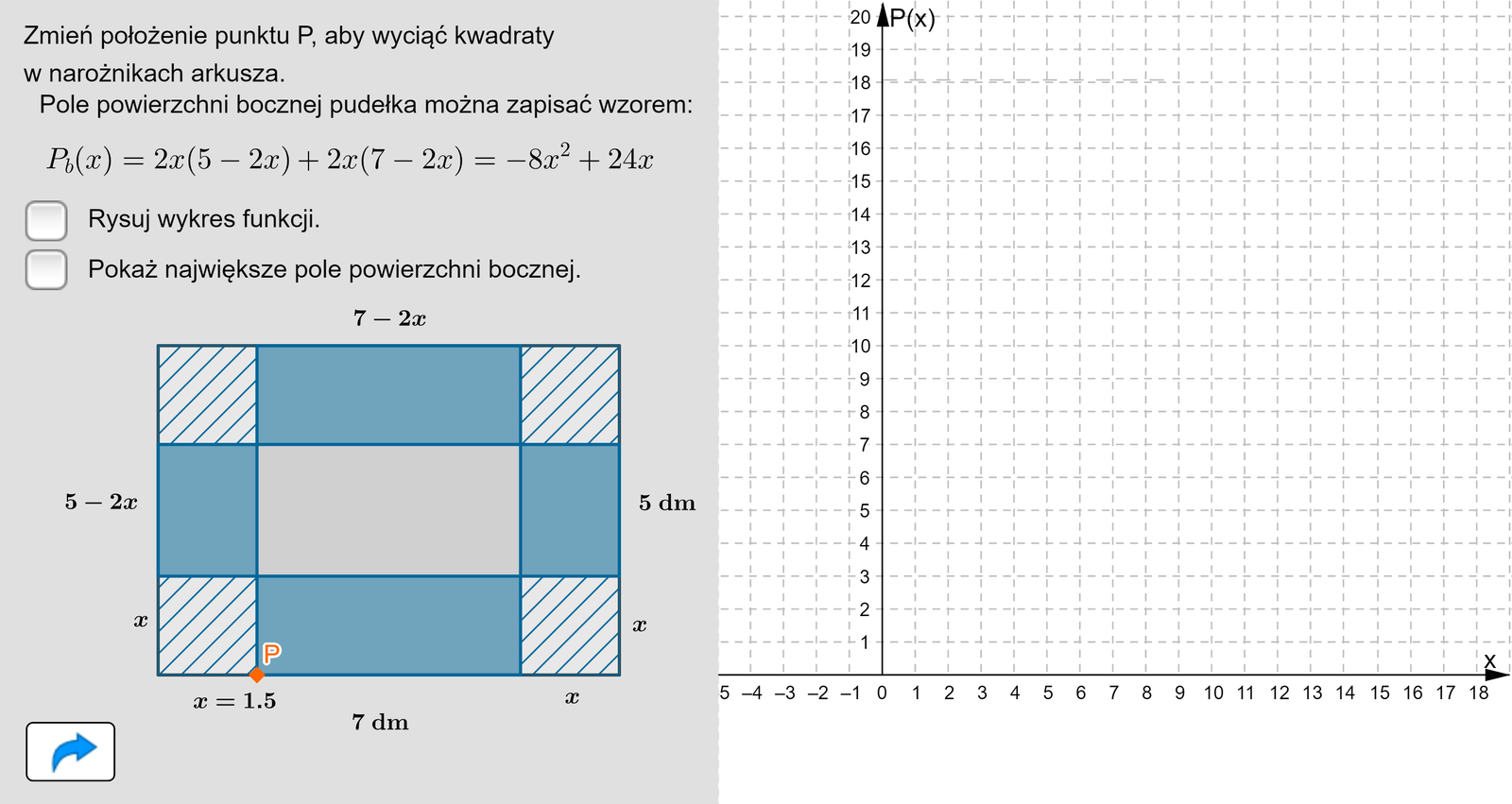
Z prostokątnego arkusza tektury o wymiarach
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/P1Ev29y4I
Suma długości przyprostokątnych trójkąta prostokątnego jest równa
Oznaczmy przez
Wiadomo, że
Stosując twierdzenie Pitagorasa, zapisujemy kwadrat
Otrzymaną funkcję kwadratową
Parabola o równaniu
Ponieważ
Zauważmy, że wtedy ten trójkąt jest równoramienny, a każda z przyprostokątnych ma długość
Właściciel sklepu z odzieżą sprowadza z hurtowni koszulki, płacąc po
Przyjmijmy, że cenę koszulki obniżano
gdzie
Rozpatrzmy funkcję
Jest to funkcja kwadratowa, której wzór możemy zapisać w postaci iloczynowej
Parabola będąca wykresem funkcji
Zatem dla
Dla tej wartości
Uwaga:
W powyższym przykładzie funkcja
Wykażemy, że jeśli
Z zależności
Zapisujemy sumę
Otrzymaną funkcję kwadratową
Parabola o równaniu
Ponieważ
Oznacza to, że jeśli
-
1 -
2 -
3 -
7
-
– 35 -
- 16 -
– 15 -
– 12
-
5 -
7 -
8 -
9
-
– 51 -
– 23 -
– 18 -
– 3
-
c = - 12 -
c = 1 -
c = 3 -
c = 5
Na rysunku przedstawiony jest wykres funkcji kwadratowej

Na rysunku przedstawiony jest wykres funkcji kwadratowej

Oblicz wartość najmniejszą oraz wartość największą funkcji kwadratowej
Funkcja
jej wartość najmniejszą w przedziale
- 2 , 3 jej wartość największą w przedziale
- 2 , 3
Wykaż, że jeśli
Wykaż, że jeśli
Wykaż, że jeśli
Wykaż, że jeśli
Wykaż, że jeśli
Wykaż, że jeśli