Wektory dla każdego

W życiu wyróżniamy dwa rodzaje wielkości, wielkości skalarne i wielkości wektorowe. Bardzo ważne jest prawidłowe posługiwanie się szczególnie wielkościami wektorowymi. W poniższym materiale znajdziesz programy ilustrujące: metodę dodawania wektorów, metodę rozkładu wektorów na składowe i zasadę równowagi trzech sił.

Wielkości skalarne

Wielkości skalarne są to wielkości fizyczne, które charakteryzowane się tylko przez jedną liczbę rzeczywistą wraz z odpowiednią jednostką. Przykładem wielkości fizycznej skalarnej jest np.: droga, energia, masa, czas czy ładunek elektryczny.

R4O3gUSiEEmki

Ilustracja przedstawia wagę i wzniesienie o kształcie trójkąta prostokątnego. Na wadze położone jest jabłko, na ekranie wagi wyświetlona jest waga jabłka zero przecinek osiemdziesiąt kilograma. Na wzniesieniu położona jest kula. Pod wzniesieniem znajduje się zielona linijka.

Pamiętaj, że poza liczbą w przypadku wielkości fizycznych ważna jest także jednostka! Dwa kilogramy jabłek nie mogą równać się dwóm kulombom ładunku elektrycznego.

R11PhbfRhmEGC

Ilustracja przedstawia trzy jabłka, znak nierówności, a za nim szare koło, które posiada w środku pięć małych kółeczek z plusikami. Pod jabłkami w zielonej ramce jest napisane em równa się dwa kilogramy, pod szarym kółkiem napisane jest ku równa się dwa kulomby.

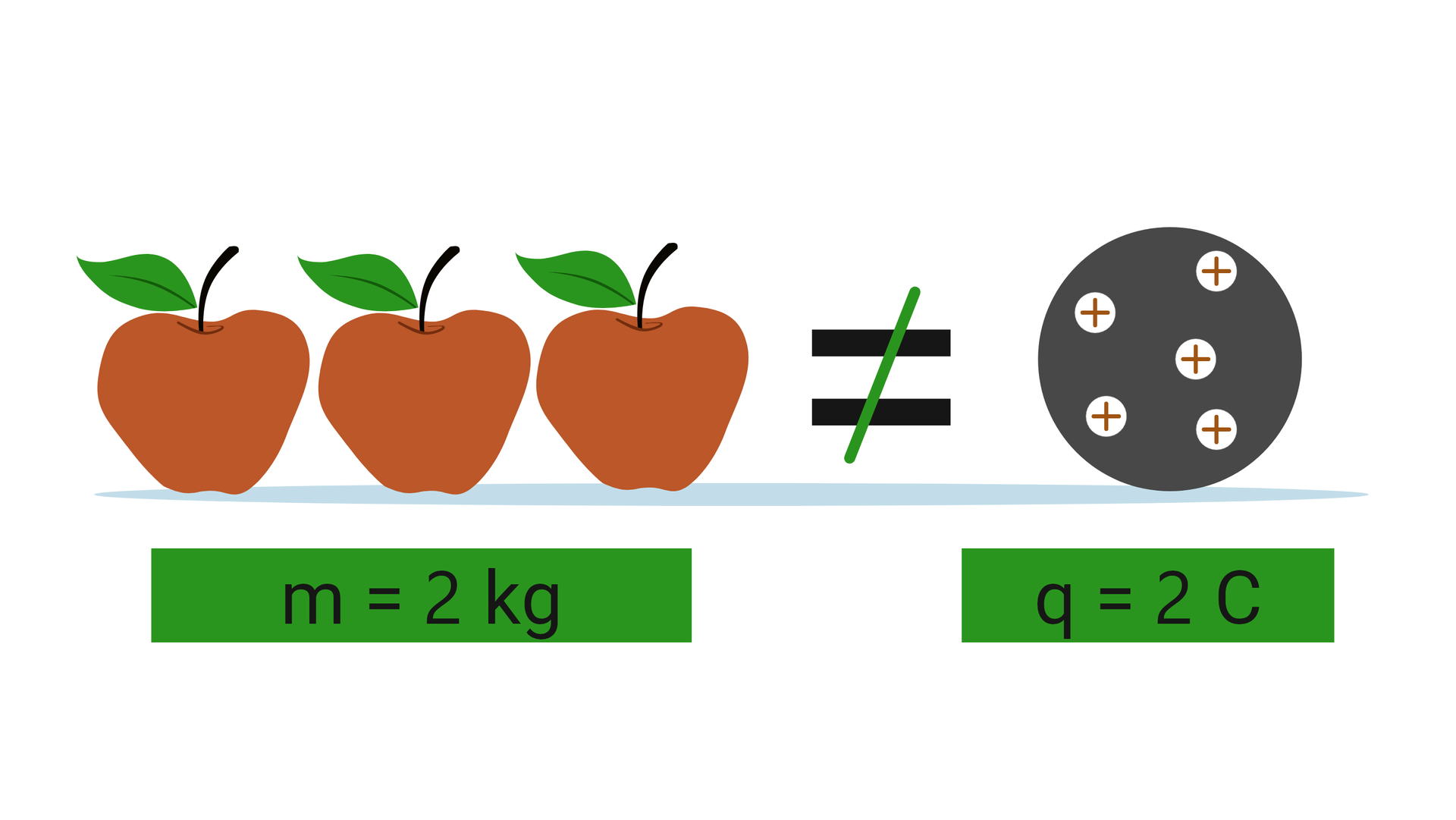
Pamiętaj, że w przypadku obliczeń dodawać możesz tylko dwie wielkości fizyczne, których jednostka jest taka sama.

Wielkości wektorowe

Wielkości wektorowe są to wielkości fizyczne, które poza swoją wartości¡ posiadają także kierunek, zwrot i punkt przyłożenia. Przykładami takich wielkości są: siłasiłasiła, przyspieszenie, prędkośćprędkośćprędkość czy pęd. W przypadku wielkości wektorowych poza samą wartością bardzo ważny jest kierunek działania opisywany przez kierunek (prostą na której lewy wektor) i zwrot (orientacją wektora na tej prostej).

RErEruMlAaFr3

Ilustracja przedstawia pojazd na górnej granicy okręgu. Widoczny na nim jest wektor prędkości skierowany w prawo, oznaczony literą V oraz wektor siły dośrodkowej skierowany w dół, oznaczony literą F z indeksem dolnym d. Wektor siły dośrodkowej jest prostopadły do wektora prędkości.

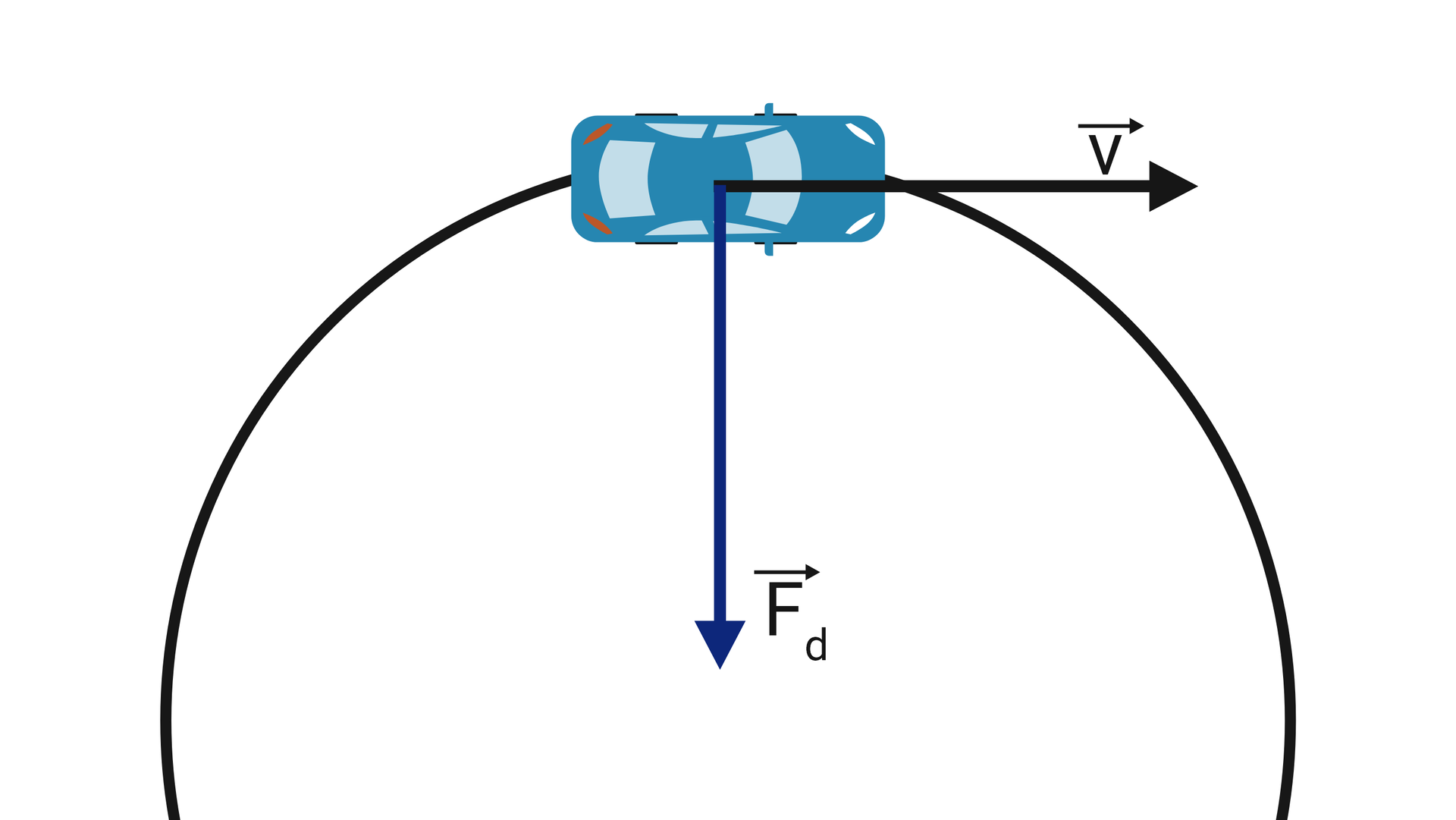
Wartości wielkości posiada także odpowiednią jednostkę np. w przypadku siły jest to niuton $\left[\vec{F}\right]=\text{N}$, a prędkośćprędkośćprędkość może to być $\left[\vec{v}\right]=\frac{\text{m}}{\text{s}}$.

RjH5qAyKzioT8

Ilustracja przedstawia cechy wektora. Widoczna jest zielona prosta, o kierunku poziomym wykonana przerywaną linią, przy niej jest napis Kierunek. Na środku linii przerywanej widoczny jest niebieski odcinek, który na prawym końcu posiada grot strzałki, przy grocie znajduje się napis Zwrot. Ze skrajnego lewego i skrajnego prawego punktu strzałki, poprowadzone są w dół prostopadłe do strzałki linie, między nimi jest ciągła linia dotykająca linii prostopadłych, pod nimi jest napisane Długość wektora myślnik Wartość. Przy lewym skrajnym punkcie wektora jest napis Punkt przyłożenia.

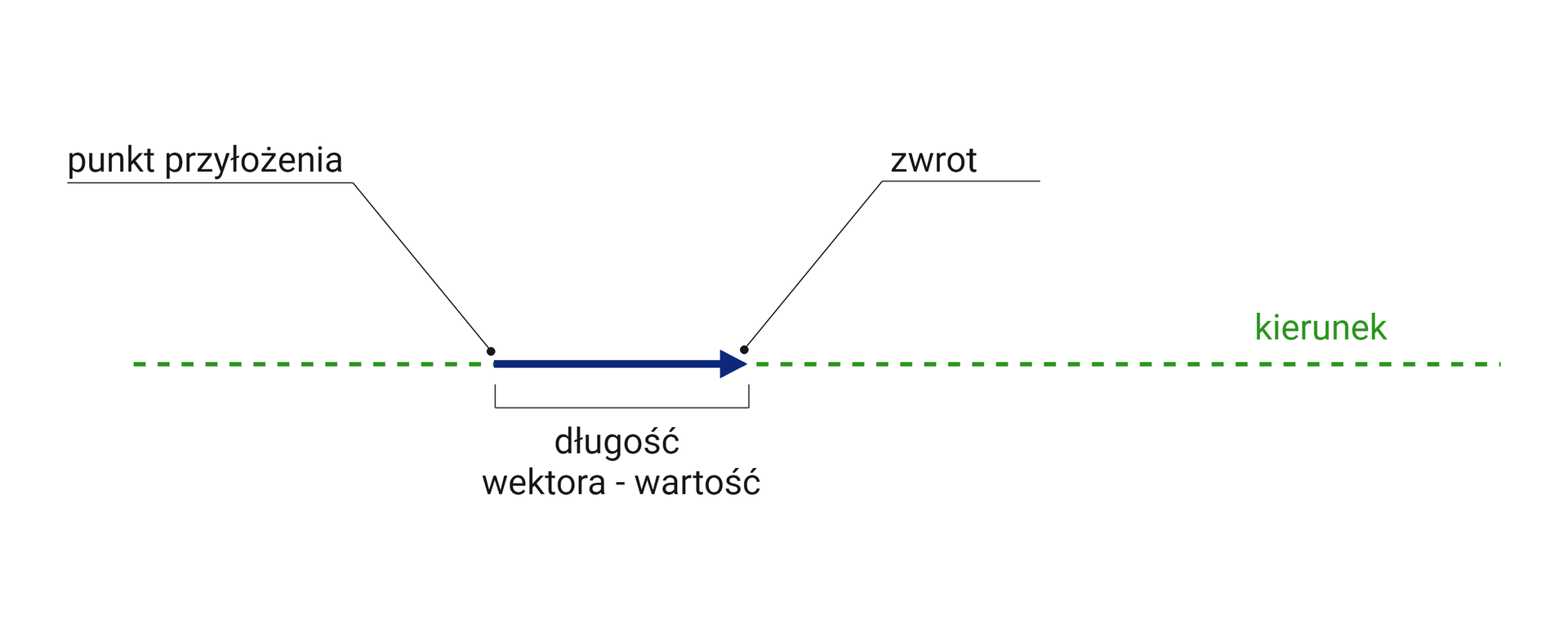
Działania na wektorach

Dodawanie czy odejmowanie wielkości fizycznych wektorowych nie jest już takie proste jak w przypadku wielkości skalarnych. Poza tym, występuje także nowy rodzaj operacji - rozkład wektora na składowe. Mnożenie wektorów w sensie podobnym jak w przypadku wielkości skalarnych nie występuje.

Dodawanie wektorów

W przypadku wektorów ze względu na to, że poza ich długością ważny jest także kierunek działania, nie możemy wektorów dodawać, dodając po prostu ich wartości. Dodawać możemy tylko wektory mające ten sam punkt przyłożenia. Możemy rozpatrzyć kilka przypadków wektorów do dodania:

• gdy wektory mają ten sam kierunek,

• nie ma tego samego kierunku.

Graczne dodawanie wektorów możemy wykonać na dwa sposoby.

Metoda równoległoboku

Ta metoda służy do dodawania tylko dwóch wektorów. Aby dodać dwa wektory należy:

1. narysować nowe wektory o tej samej długości kierunku i zwrocie jak dodawane wektory tak, aby początek każdego z nowych wektorów znajdował się w końcu drugiego z wektorów, w ten sposób powinien powstać równoległobok,

2. narysować wektor mający początek w punkcie, w którym początek miały dodawane wektory i koniec w punkcie, w którym mają końce przesunięte równolegle wektory, wektor ten leży na tej przekątnej równoległoboku, której jeden z końców jest w punkcie przyłożenia obydwu dodawanych wektorów. Wektor ten jest sumą tych dwóch wektorów.

Sposób postąpowania zilustrowany jest na grafice poniżej.

REaMESVqaMEAK

Ilustracja przedstawia przykład użycia metody równoległoboku. Na pierwszym rysunku widoczne są dwa wektory: wektor A skierowany w lewy górny róg oraz wektor B zaczynający się przy punkcie początkowym wektora A, skierowany w prawy górny róg. Na drugim rysunku dodano wektory A prim i B prim. Przy grocie wektora A poprowadzony został wektor A prim skierowany w prawo, a z grota wektora B poprowadzony został wektor B prim skierowany w górę. Z dodanych wektorów powstał równoległobok. Trzeci rysunek przedstawia sumę wektorów A i B, oznaczoną jako wektor A plus wektor B. Jego grot łączy się z grotem wektorów B prim i A prim. Obok znajduje się zapis sumy wektorów: A plus B.

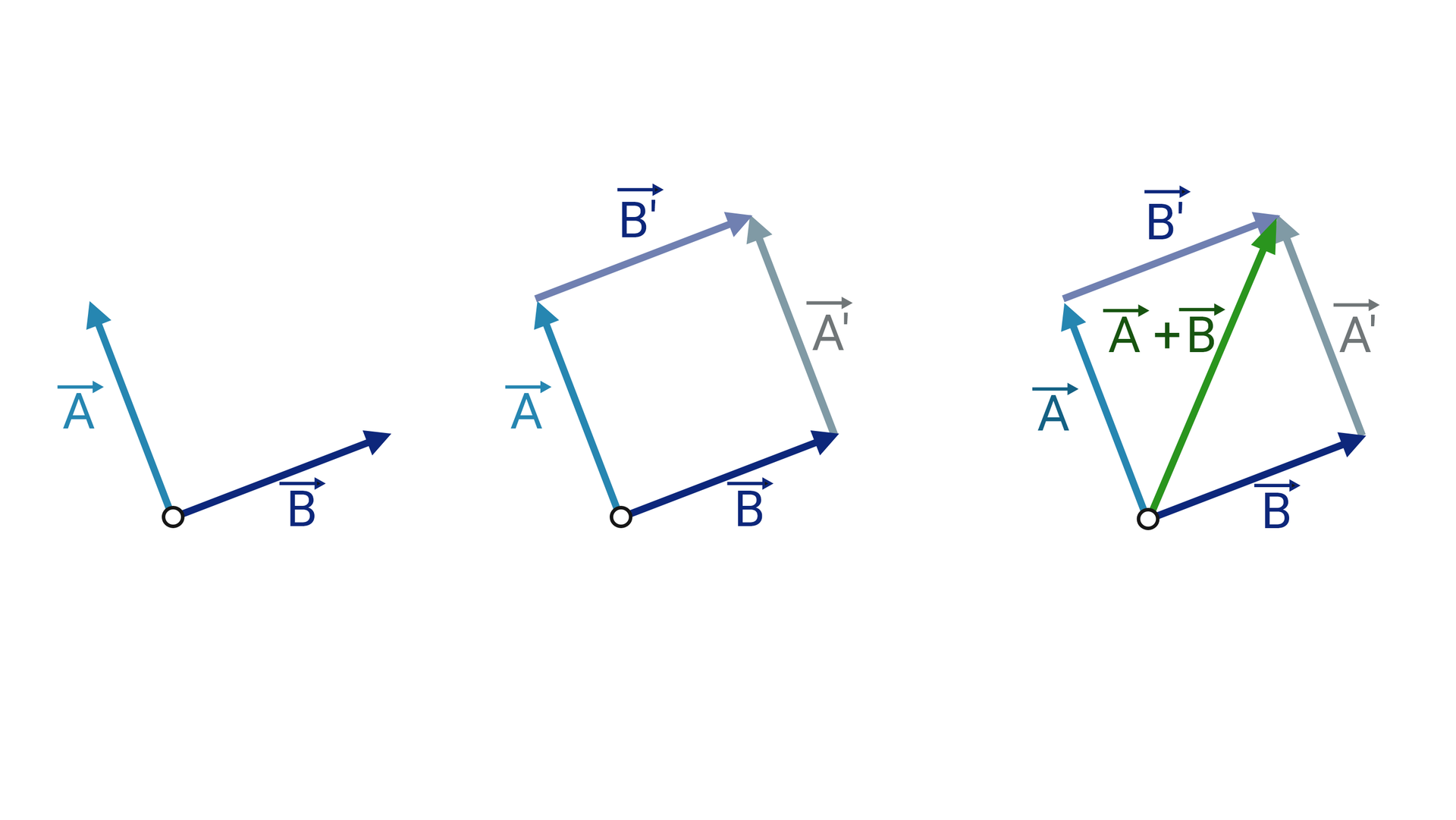
Zauważ, że wynikowy wektor nie musi mieć długości równej sumie długości wektorów dodawanych.

Metoda trójkąta

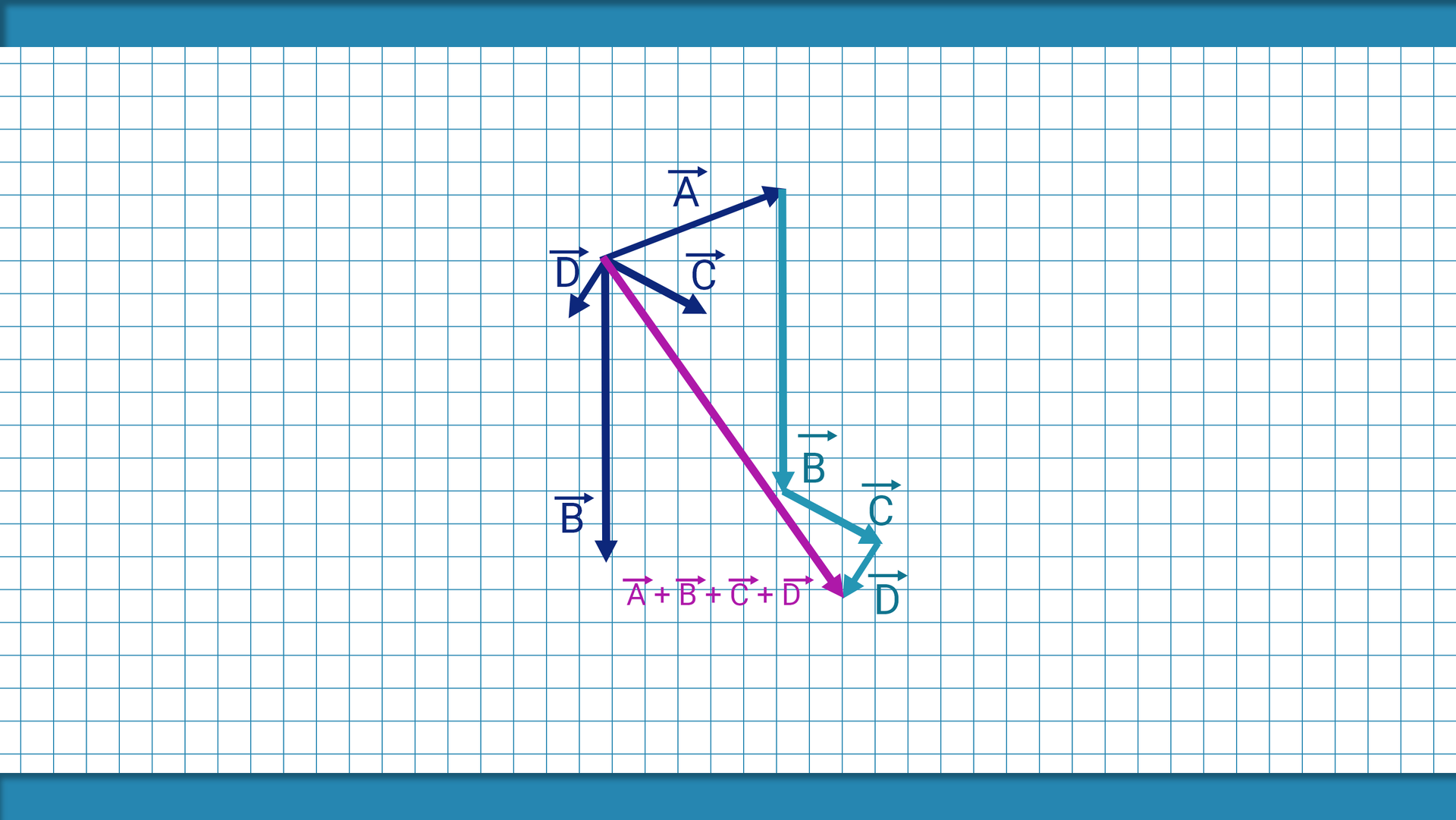
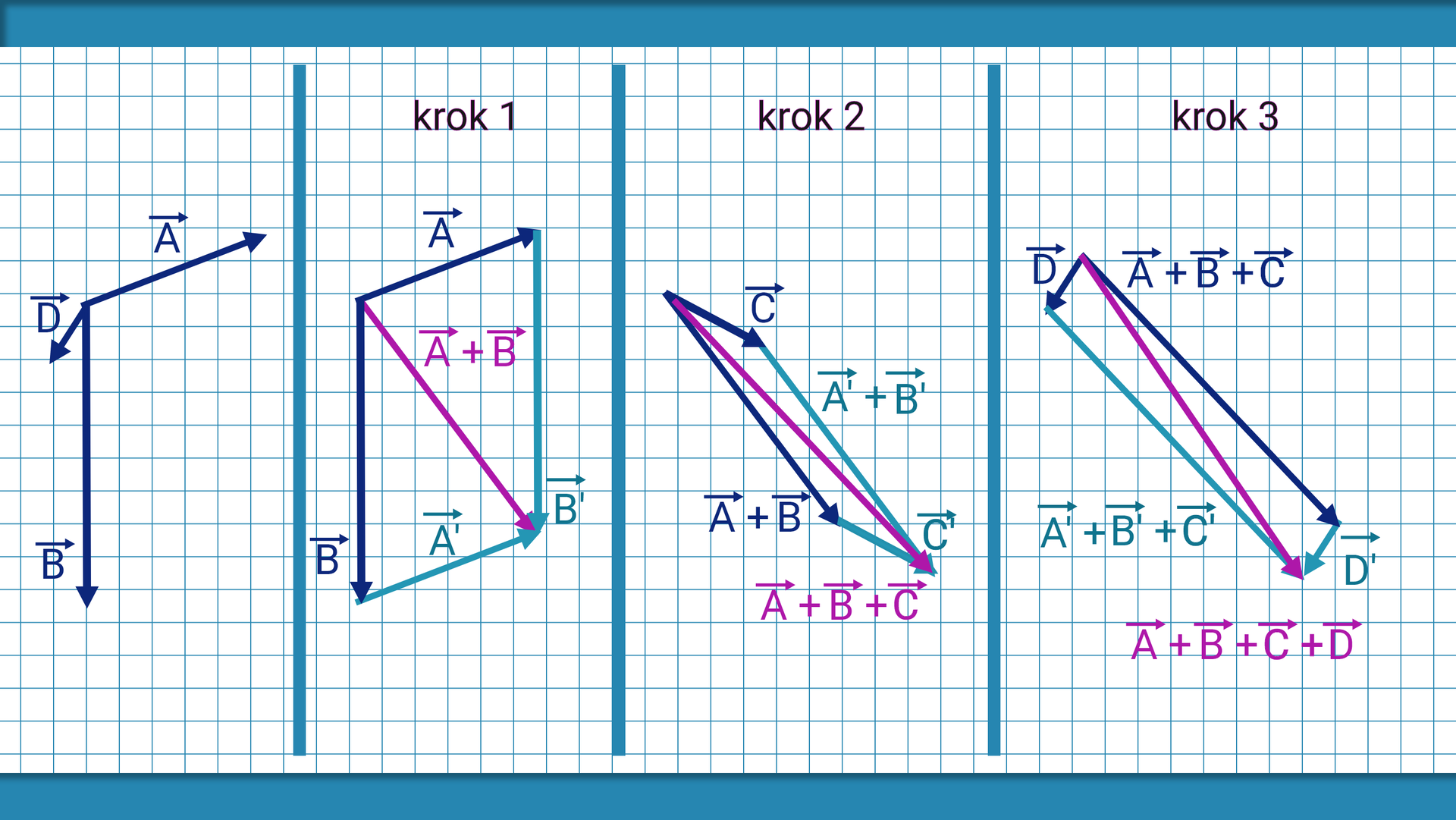
Druga metoda może być wykorzystana do dodawania dwóch i więcej wektorów. Aby z jej pomocą znaleźć wektor będący sumą kilku wektorów należy:

1. po kolei przenosić równolegle wektory tak aby punkt końcowy pierwszego wektora był punktem przyłożenia drugiego, punkt końcowy drugiego był punktem przyłożenia trzeciego itd.

2. narysować wektor mający punkt przyłożenia w punkcie przyłożenia pierwszego wektora i koniec w punkcie końcowym ostatniego wektora, wektor ten jest wynikiem dodawania tych wektorów.

Sposób postąpowania zilustrowany jest na grafice poniżej.

R1IkD8LgMh6YJ

Ilustracja przedstawia dodawanie trzech wektorów metodą trójkąta. Na pierwszym rysunku widoczne są trzy wektory tworzące literę "Y": wektor A skierowany w lewym górnym kierunku, wektor B skierowany w prawym górnym kierunku i wektor C skierowany w dół. Na drugim rysunku wektor A zmienił położenie, jego punkt początkowy znajduje się na dole, a koniec łączy się z punktem przyłożenia wektora B. Punkt końcowy wektora B staje się punktem przyłożenia wektora C, który jest skierowany w dół. Na trzecim rysunku dorysowany został wektor, którego punkt początkowy znajduje się w punkcie przyłożenia wektora A, a koniec w punkcie końcowym wektora C. Obok znajduje się zapis sumy wektorów: A plus B plus C.

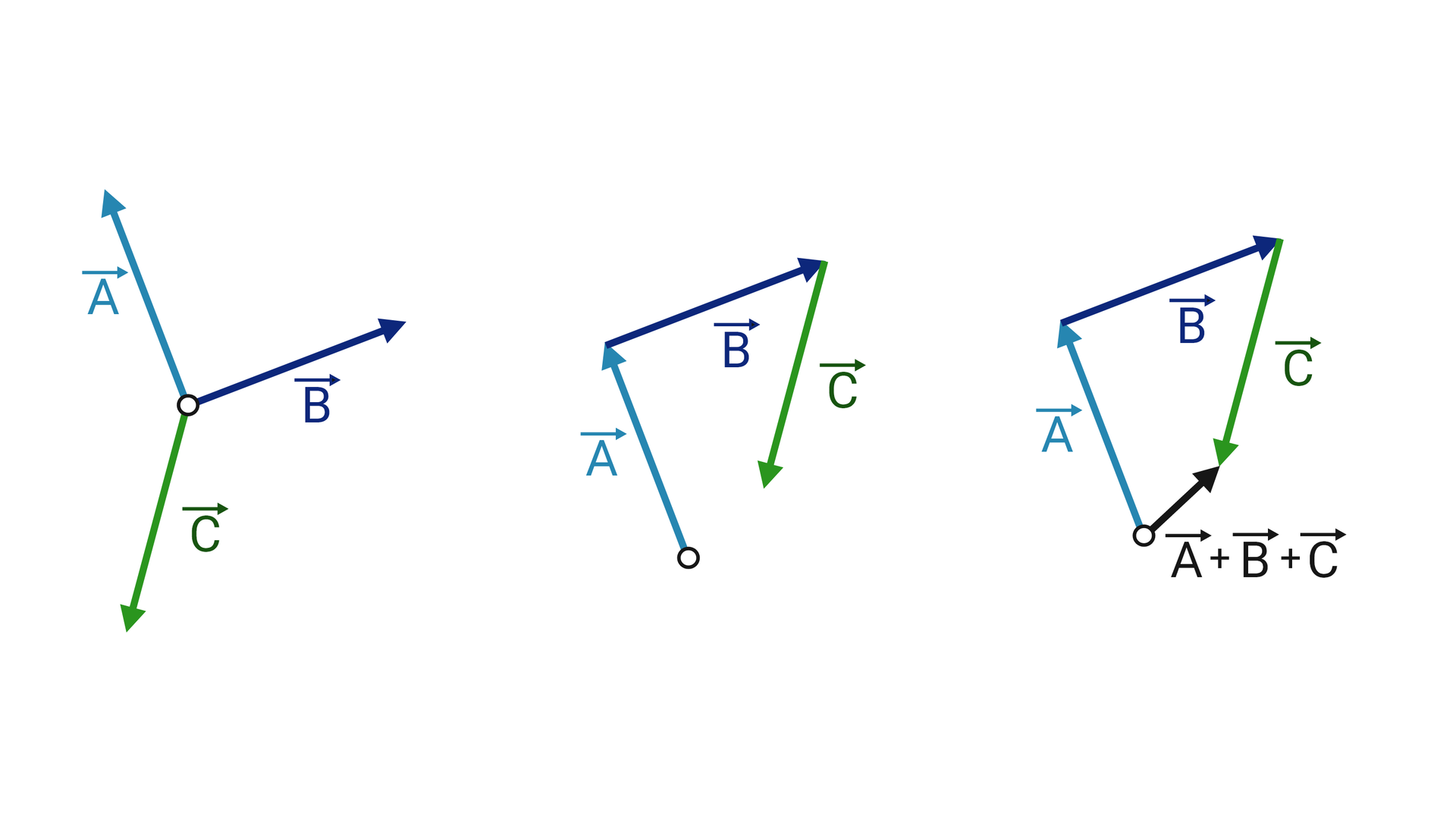
Metoda ta bierze swoją nazwę z figury jaka powstaje po przesunięciu i narysowaniu wektora wynikowego w przypadku dodawania dwóch wektorów.

RumrsF0YiglNN

Ilustracja przedstawia dodawanie dwóch wektorów metodą trójkąta. Na pierwszym rysunku widoczne są dwa wektory: wektor A skierowany w górę oraz wektor B zaczynający się przy punkcie początkowym wektora A, skierowany w prawo. Na drugim rysunku wektor B zmienił położenie, tak że punkt końcowy wektora A, stał się jego punktem początkowym, wektor skierowany jest w prawo. Na trzecim rysunku z punktu początkowego wektora A poprowadzony został wektor, tworzący sumę wektorów A i B. Punkt końcowy wektora A plus B znajduje się w punkcie końcowym wektora B. Obok jest zapis wektor A plus wektor B.

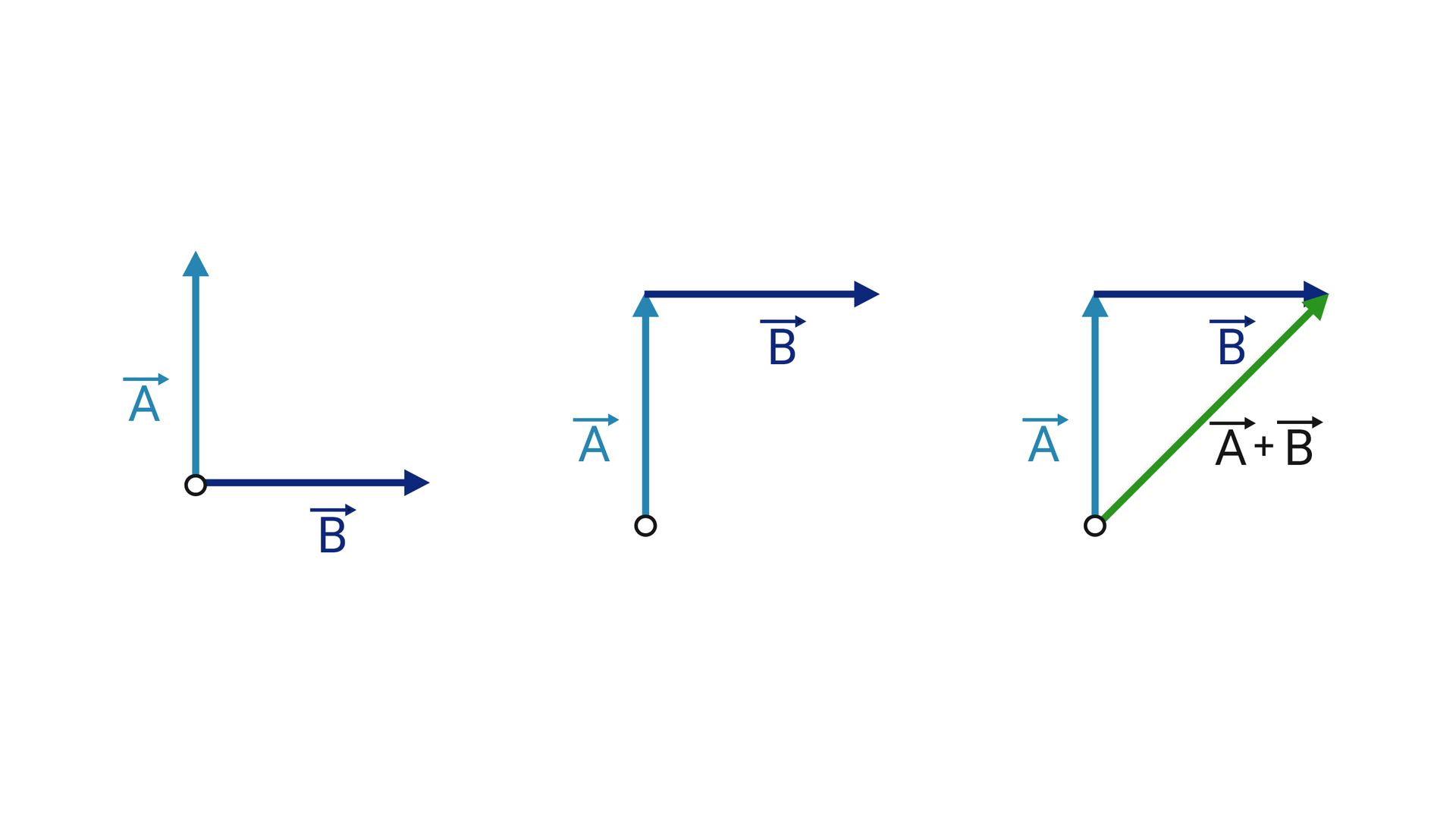
W przypadku dodawania więcej niż dwóch wektorów powinniśmy ją nazywać metodą wieloboku.

Metodę tę wykorzystuje zamieszczony w tym materiale program.

Odejmowanie wektorów

Gdy odejmujemy wektor $\vec{B}$ od wektora $\vec{A}$ to możemy to równoważnie rozpatrzyć jako dodawanie do wektora $\vec{A}$ wektora $-\vec{B}$. Wektor $-\vec{B}$ nazywany jest wektorem przeciwnymwektor przeciwnywektorem przeciwnym do wektora $\vec{B}$ i ma taką samą długość i kierunek jak wektor $\vec{B}$, lecz przeciwny zwrot.

RmJWGViLwe9QP

Ilustracja przedstawia wektor przeciwny. Widoczne są dwa wektory, pierwszy jest to wektor B skierowany w prawym górnym kierunku, drugi wektor jest to wektor minus B, skierowany w lewym dolnym kierunku.

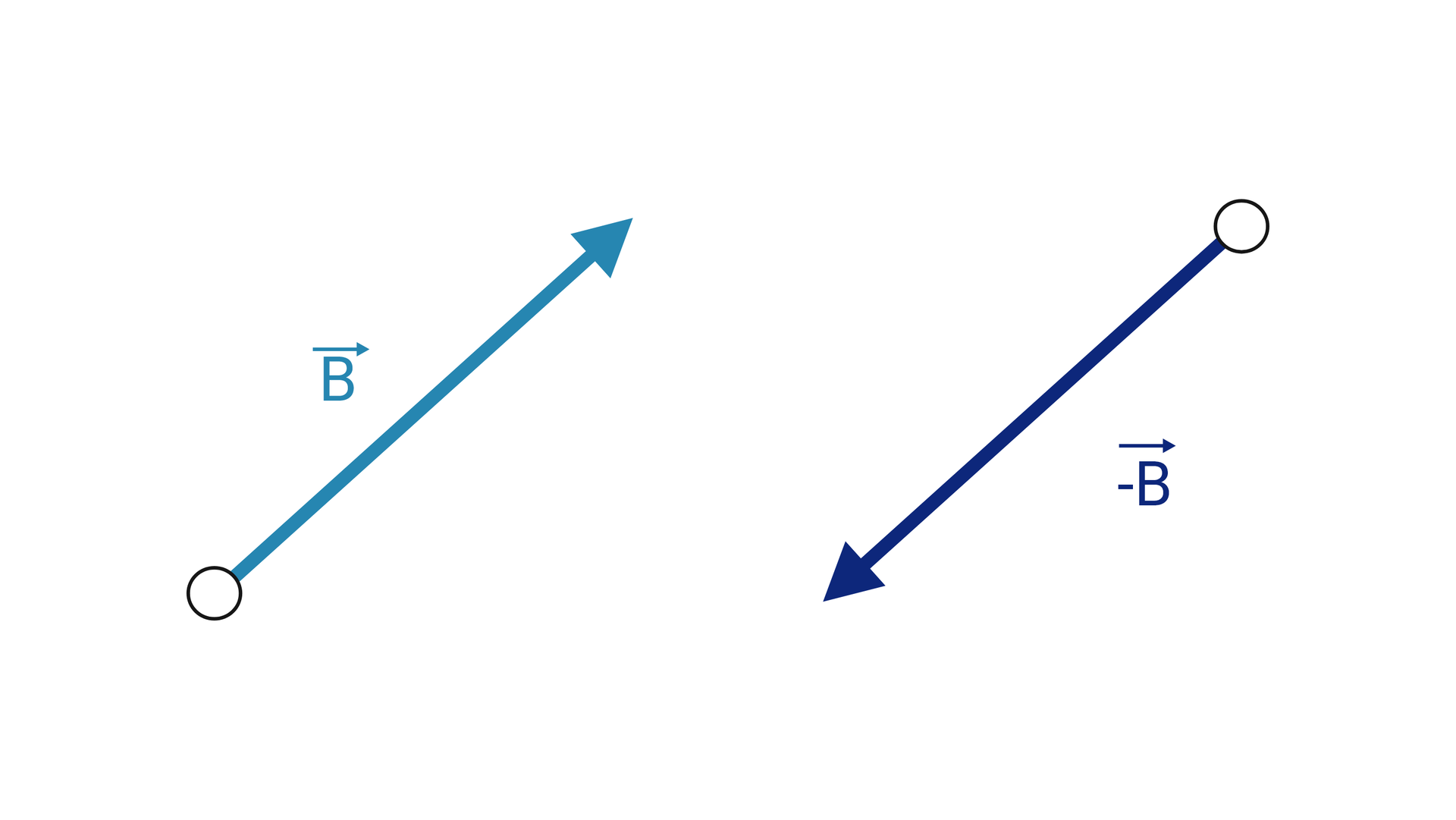
Stąd odejmowanie wektorów możesz wykonać wykorzystując metody dodawania wektorów.

Rozkład wektora na składowe

Wektor można rozłożyć także na wektory składowe. Jest to niejako operacja odwrotna do dodawania wektorów. Chcąc poznać wektory, które zostały dodane, aby powstał dany wektor należy wybrać dwie proste przechodzące przez początek rozkładanego wektora oraz:

1. narysować proste równolegle do zadanych prostych przechodzące przez koniec wektora rozkładanego na skladowe,

2. narysować na każdej prostej wektor mający punkt przyłożenia w puncie, w którym ma punkt przyłożenia rozkładany wektor, a punkt końcowy w punkcie przecięcia prostych, wektor ten zawierać ma się w jednej z zadanych prostych. Drugi wektor powstaje analogicznie.

Rfg2utbmgngOE

Ilustracja przedstawia rozkład wektora na składowe. Na pierwszym rysunku widoczny jest wektor A skierowany w lewym górnym kierunku, w punkcie początkowym wektora przecinają się dwie proste. Na drugim rysunku widoczne są dodatkowo dwie proste równoległe do prostych z pierwszego rysunku, przecinające się na końcu wektora A. Na trzecim rysunku widoczne są dodatkowe dwa wektory B i C, mające punkt przyłożenia w punkcie, w którym punkt przyłożenia ma wektor A. Wektor B punkt końcowy ma w puncie przecięcia się prostych po lewej stronie, a wektor C ma punkt końcowy w punkcie przecięcia się prostych po prawej stronie.

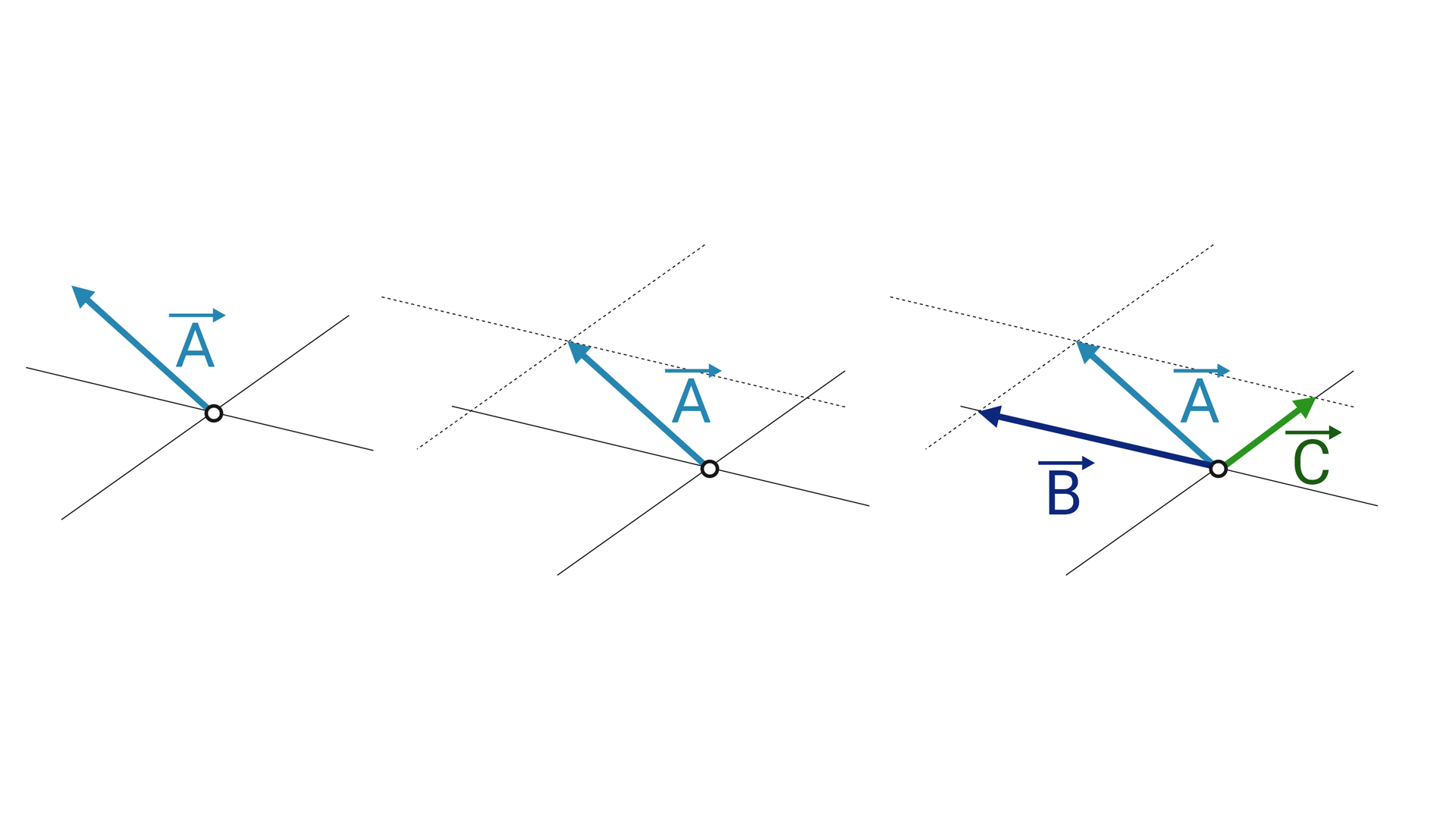
Szczególnym przypadkiem tej operacji, często wykorzystywanym w życiu, jest rozkład wektora na składowe prostopadłe zilustrowany na grafice poniżej.

RLt3YnFpxewCK

Ilustracja przedstawia rozkład wektora na składowe prostopadłe. Na pierwszym rysunku widoczne są prostopadłe linie tworzące układ współrzędnych i wektor A skierowany w prawym górnym kierunku. Na drugiej ilustracji do wektora A, zostały dorysowane dwie prostopadłe linie od punktu końcowego wektora do pionowej i poziomej linii osi. Na trzeciej ilustracji na podstawie poprowadzonych wcześniej linii, na poziomej linii osi został dorysowany wektor skierowany w górę, a na poziomej linii osi wektor B skierowany w prawo.

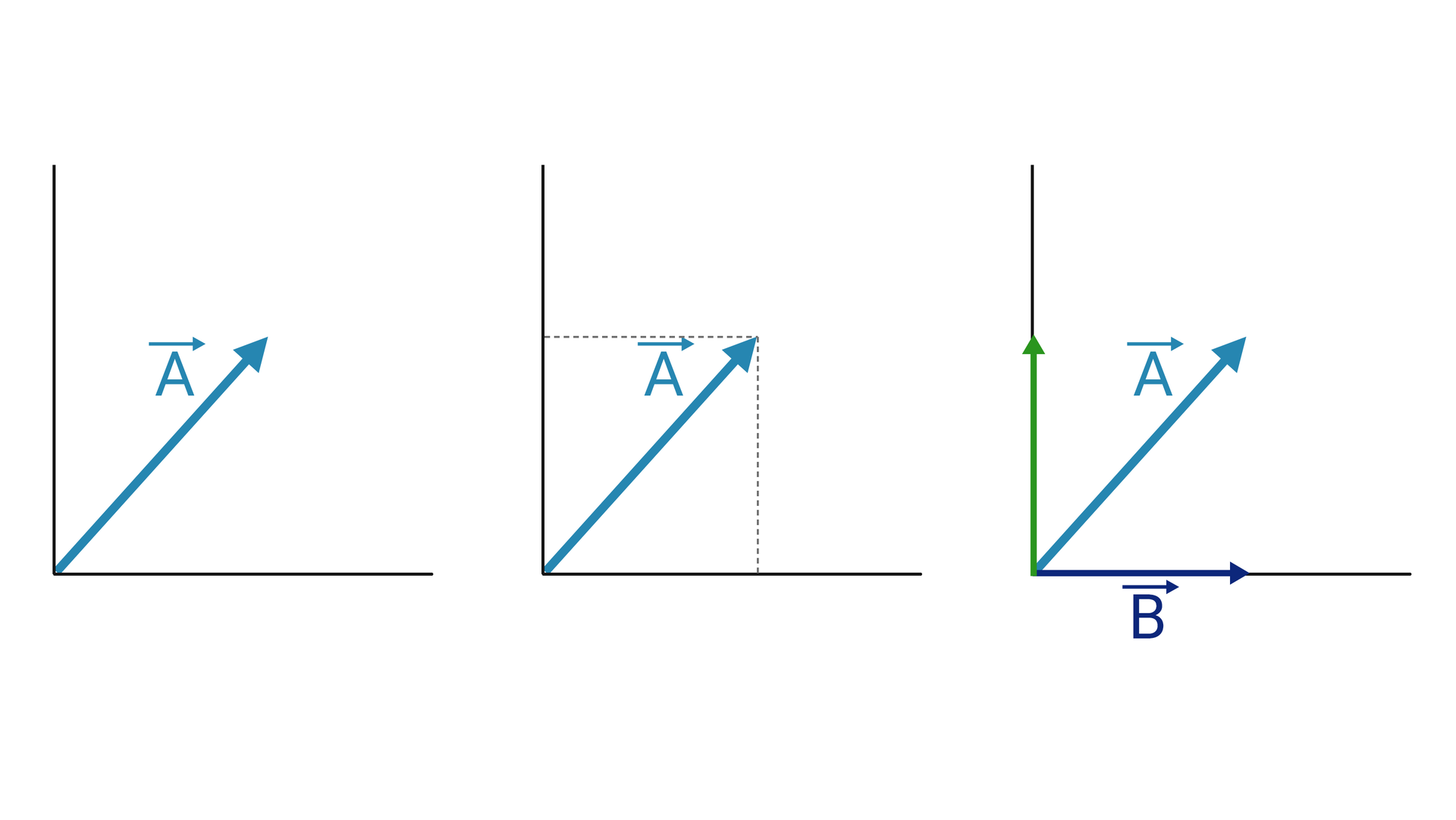
Przeprowadzenie tej operacji obrazuje druga część programu.

Równowaga trzech sił

Trzy siły znajdują się w równowadze kiedy:

1. proste na których leżą zawierają się w jednej płaszczyźnie oraz przecinają się w jednym punkcie,

2. wektory sił tworzą trójkąt.

Najprościej sytuację tę możemy zobaczyć gdy na cienkiej i nieważkiej lince powieszone zostaną trzy ciężarki: dwa na końcach i jeden pośrodku. Wtedy gdy masa dowolnych dwóch ciężarków jest większa od masy trzeciego, to ciężarki te przemieszczą się, lecz nie spadną. Pomiędzy linką, a kierunkiem pionowym w punkcie zawieszenia ciężarka pomiędzy bloczkami ustalą się takie kąty, aby po dodaniu wszystkich wektorów ich suma wynosiła zero, a zatem spełniona była $\text{I}$ zasada dynamiki Newtona$\text{I}$ zasada dynamiki Newtona$\text{I}$ zasada dynamiki Newtona.

RC4c43K0iiJey

Ilustracja przedstawia równowagę trzech sił. Widoczne są dwa bloczki ustawione na słupkach o tej samej wysokości. Przez bloczki przewieszona jest nieważka nic, na której zawieszono trzy ciężarki o różnych masach, dwa na końcach nici i jeden między ciężarkami. Ciężarki na końcach nici mają masy podpisane jako m jeden oraz m dwa, a ciężarek na środku ma masę m trzy. Każdy ciężarek jest również ściągany w dół odpowiednimi siłami ciężkości o wektorach F c jeden, dwa i trzy. Ciężarek pomiędzy bloczkami zawieszony jest na niciach pod kątem. Przez punkt zawieszenia tego ciężarka przechodzi pionowa linia przerywana. Kąty między tą pionową linią a odcinkami nici są zaznaczone odpowiednio jako kąt alfa oraz kąt beta. Z punktu zawieszenia ciężarka trzeciego na nici odchodzą trzy wektory sił. Te siły to kolejno: F jeden, pochodząca od ciężarka pierwszego, F dwa, pochodząca od ciężarka drugiego, oraz F trzy od ciężarka trzeciego. F jeden i F dwa są skierowane wzdłuż nici pod kątami odpowiednio beta oraz alfa od pionu i w kierunku bloczków, a wektor F trzy skierowany jest pionowo w dół.

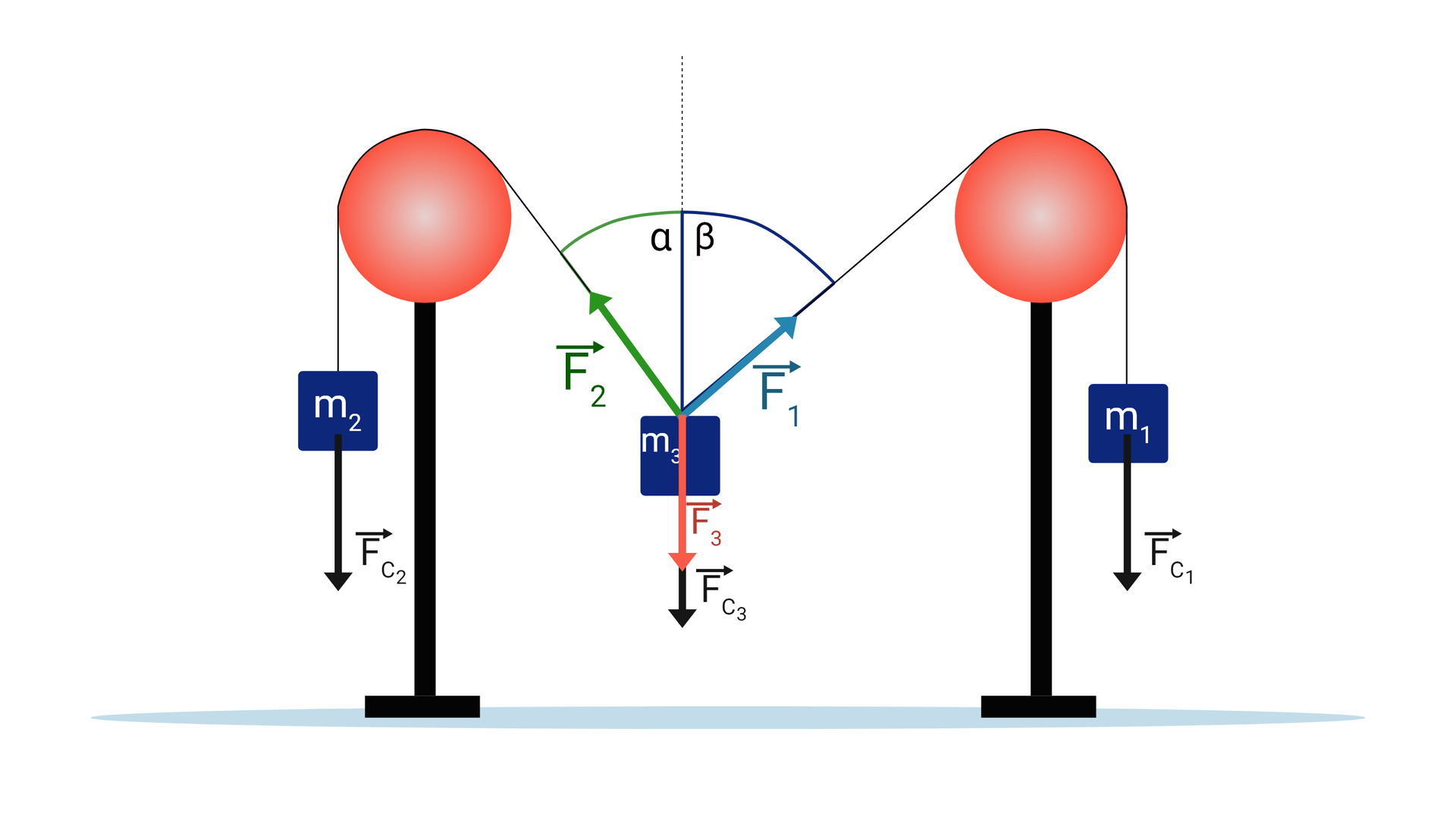
Aby lepiej zrozumieć tę sytuację zajrzyj do trzeciej części programu.

Rozkład sił na równi pochyłej

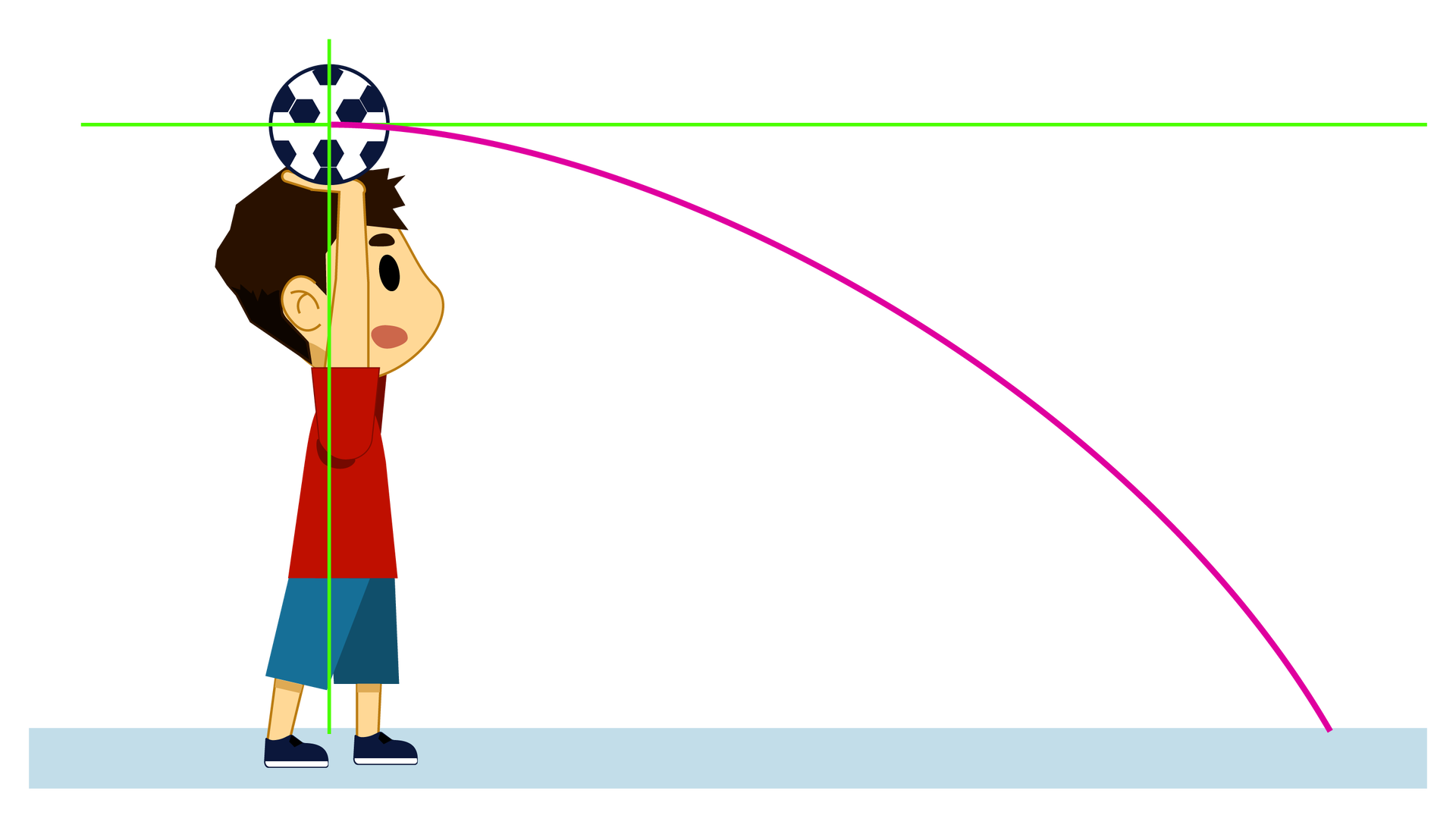
Jedną z sytuacji, w których wykorzystuje się rozkład wektorów na składowe jest rozwiązywanie zadań związanych z dynamiką ciała znajdującego się na równi pochyłej. Rozwiązując dowolny problem ruchu ciała w więcej niż jednym wymiarze konieczne jest rozłożenie wszystkich sił działających na ciało (a także innych wielkości wektorowych, które mają wpływ na ruch, jak np. prędkość) na prostopadłe do siebie kierunki, w ten sposób możemy osobno opisywać ruch względem każdego z tych kierunków. Wybór kierunków, względem których będziemy opisywać ruch jest dowolny, jednak zazwyczaj wybieramy taką orientację jednego z kierunków, aby opis ruchu był jak najprostszy. W przypadku opisu ruchu rzuconej znad głowy piłki przed siebie wszystkie wektory będziemy rozkładać względem kierunków: równoległego do ziemi i prostopadłego do niego.

R1eQyGWq5E3Kw

Na ilustracji widoczny jest chłopiec rzucający piłkę znad głowy w kierunku poziomym. Od piłki poprowadzone są zielone linie, równoległa do podłoża i prostopadła do niego oraz krzywa koloru różowego prowadząca od piłki w kierunku podłoża, przedstawiająca tor spadku piłki.

W przypadku równi pochyłej rozkładu sił możemy dokonać równolegle do podłoża (i prostopadle do niego) - w kierunku zgodnym z kierunkiem wektora siły ciężkości lub równolegle do powierzchni równi i prostopadle do niej - w kierunku zgodnym z kierunkiem wektora siły reakcji podłoża. Zazwyczaj wybieramy drugi sposób rozkładu wektorów, ze względu na dużo prostszy opis matematyczny ruchu w takim układzie.

R1F8qVsLxQvBc

Na ilustracji widoczna jest równia pochyła ustawiona na podłodze, a na niej znajduje się prostokąt. Przez środek prostokąta przechodzą cztery proste, dwie bordowe i dwie granatowe. Jedna z prostych w kolorze bordowym jest równoległa do podłogi, druga prosta w kolorze bordowym jest prostopadła do niej. Jedna z prostych w kolorze granatowym jest równoległa do powierzchni równi, a druga prosta granatowa jest prostopadła do niej.

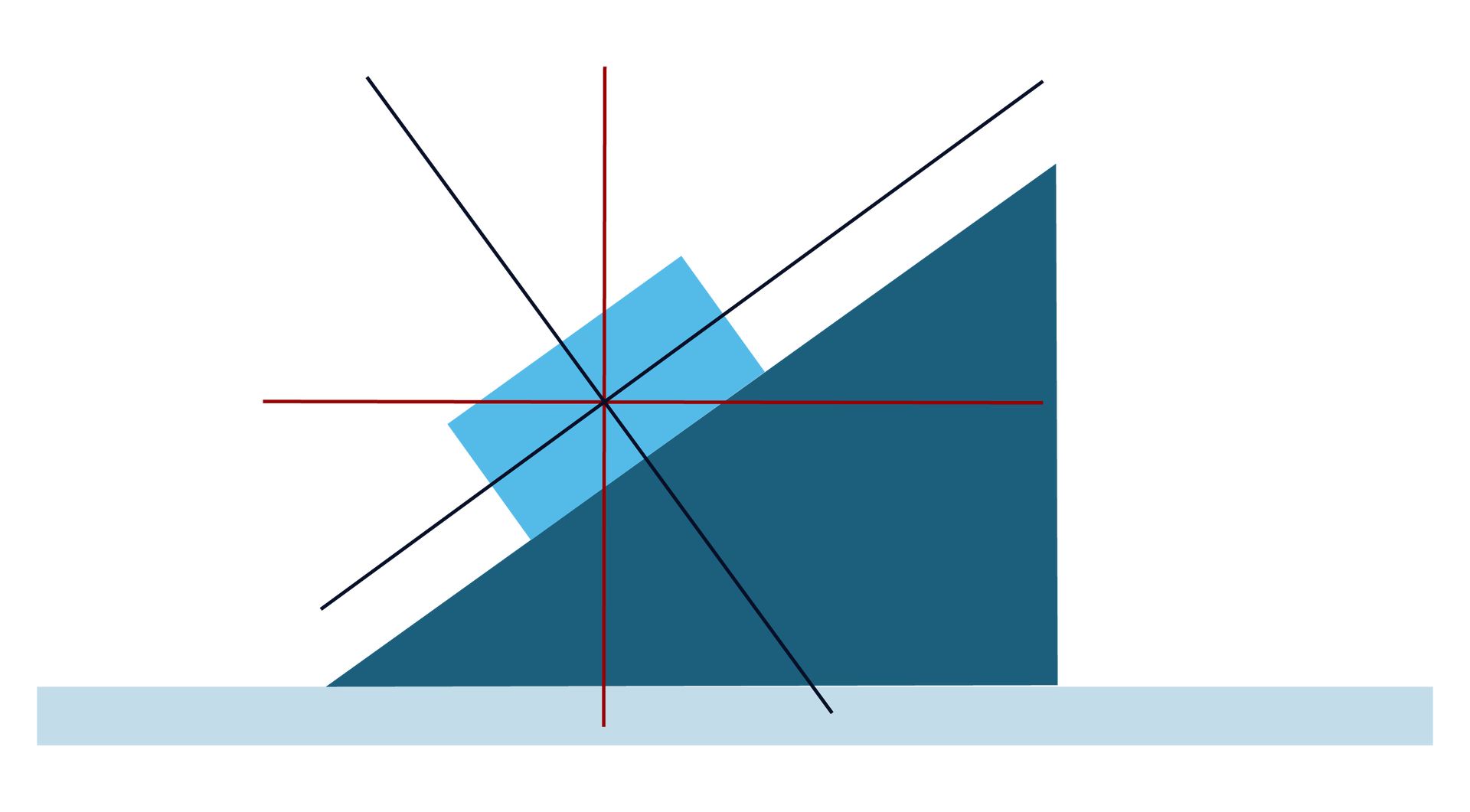
W przypadku rysowania sił działających na ciało na równi pochyłej ważne jest, aby w prawidłowych miejsach przykładać działające siły, gdyż ta informacja będzie kluczowa w momencie, w którym omawiać będziesz dynamikę bryły sztywnej. Pamiętaj, że siła tarcia przyłożona jest w środku odcinka stycznego pomiędzy ciałem, a równią. Zwróć także uwagę, że siła nacisku przyłożona jest do równi, a nie ciała! Do ciała przyłożona jest siła reakcji podłoża działająca w związku z $\text{III}$ zasadą dynamiki Newtona, dlatego ma ona taki sam kierunek i wartość jak siła nacisku. W programie oraz tym materiale ciało umieszczone na równi jest punktem materialnym, zatem wszystkie siły, których punkty przyłożenia znajdują się na ciele (zazwyczaj rysowanym jako kwadrat), są przyłożone w jednym punkcie, stąd możemy je sumować.

W programie poszczególne siły oznaczone są jako:
$\vec{F_\text{c}}$ - siła ciężkości,
$\vec{F_\text{N}}$ - siła nacisku,
$\vec{F_\text{R}}$ - siła reakcji podłoża,
$\vec{F_\text{T}}$ - siła tarcia,
$\vec{F_\text{P}}$ - siła prostopadła do powierzchni równi,
$\vec{F_\text{S}}$ - siła równoległa do powierzchni równi,
$\vec{F_\text{w}}$ - siła wypadkowa.

Pamiętaj, że równoważące się siły zgodnie z $\text{I}$ zasadą dynamiki powodują, że ciało porusza się ruchem jednostajnym prostoliniowym (jeśli się wcześniej poruszało) albo spoczywa. Pierwszą z opisanych sytuacji możesz zaobserwować w programie.

Program ucząco‑monitorujący do nauki zapisu wektorów

1

Instrukcja

Instrukcja

Uruchom program klikając przycisk Rozpocznij. Program możesz też otworzyć w widoku pełnoekranowym klikając przycisk w prawym dolnym rogu. Wybierz jeden z trzech programów:

• Dodawanie wektorów.

• Równowaga trzech sił.

• Rozkładanie wektorów na składowe,

• Rozkład sił na równi pochyłej.

W każdym z programów w prawym górnym rogu znajdziesz przyciski służące kolejno do: wgrania pliku tekstowego ze zdefiniowanymi parametrami programu, pobrania aktualnego stanu programu oraz powrotu do wyboru programu.

R1F6h0NeLou1y

Kolejno od lewej przyciski: wgrywania pliku, pobierania pliku, powrotu do menu wyboru programu.

W prawym dolnym rogu znajdziesz przyciski odpowiadające za oddalanie kamery, przybliżanie kamery i resetowanie widoku do domyślnego.

R1Wz21m6jLtG5

Kolejno od lewej przyciski: oddalania widoku kamery, przybliżania widoku kamery, resetowania widoku kamery.

Dodawanie wektorów

W tym programie najpierw wybierz liczbę wektorów, klikając strzałki w prawo lub w lewo znajdujące się przy polu Liczba wektorów. Aby zmienić kierunek, zwrot i długość wektora naciśnij i przytrzymaj jego koniec, przesuwając go w wybrane miejsce. Możesz w ten sam sposób przesunąć także czerwony punkt, który jest punktem przyłożenia wszystkich wektorów. Gdy ustawisz wybrane parametry, naciśnij przycisk Rozpocznij i obserwuj animację. Z listy po prawej stronie ekranu możesz odczytać współrzędne wektorów $\vec{v}_i$, które są dodawane oraz wektora $\vec{w}$ będącego sumą tych wektorów. Aby cofnąć do momentu definiowania wektorów, kliknij przycisk Restartuj.

Równowaga trzech sił

Wybierz wartość wszystkich mas, klikając strzałki w lewo lub w prawo w poszczególnych polach. Program sprawdza warunki, jakie muszą spełniać masy, dlatego możesz nie być w stanie zmniejszyć lub zwiększyć wartości danych mas. Po kliknięciu w pole Suma sił wyświetli się graficzne zsumowanie wektorów $\vec{F}_1$ oraz $\vec{F}_2$. Poniżej wyświetlają się wartości kątów $\alpha$ oraz $\beta$. Aby powrócić do początkowych ustawień masy, kliknij przycisk Restartuj.

Rozkładanie wektorów na składowe

Wybierz ułożenie punktu przyłożenia, klikając i przytrzymując przemieść w nowe miejsce czerwony punkt. Aby wybrać kierunki prostych, kliknij i przytrzymaj zaznaczony na nich punkt w kolorze prostej i przemieść w nowe miejsce. Aby zmienić długość i kierunek wektora $\vec{u}$, analogicznie kliknij i przemieść koniec wektora w wybrane miejsce. Klikając przycisk Rozpocznij włączysz animację. Naciskając przycisk Restartuj powrócisz do początkowych ustawień programu. Po prawej stronie w górnej tabeli podane są współrzędne poszczególnych wektorów, a w dolnej ich długości.

Rozkład sił na równi pochyłej

W menu z prawej strony możesz wybrać masę ciała $m$ znajdującego się na równi, wartość współczynnika tarcia $\mu$ oraz możesz zobaczyć wartości poszczególnych sił. Kąt nachylenia równi $\alpha$ możesz ustalić przesuwając niebieski punkt na górze równi lub skorzystać z menu po prawej stronie, z pomocą którego wybierzesz charakterystyczne wartości od $0^\circ$ do $90^\circ$ co $15^\circ$. Możesz także pokazać lub ukryć linie pomocnicze pochodzące z rozkładania wektora $\vec{F_c}$ na składowe oraz wektory powstałe w wyniku tej operacji, zaznaczając odpowiednie pole wyboru. Za pomocą pomarańczowego punktu możesz przesuwać kamerę. Naciśnij przycisk Rozpocznij, aby pojawiła się dodatkowa siła zewnętrzna $\vec{F_\text{z}}$, która zapewni aby klocek poruszał się ruchem jednostajnym i zobaczyć ten ruch. Aby klocek wrócił na piewotne miejsce naciśnij przycisk Restartuj, który pojawi się obok niego.

RzDj4KGox52sM

Interaktywny program ucząco‑monitorujący do nauki zapisu wektorów składa się z czterech części:

1. Dodawanie wektorów.
2. Rozkład wektorów na składowe.
3. Równowaga trzech sił.
4. Rozkład sił na równi pochyłej.

Interaktywny program ucząco‑monitorujący do nauki zapisu wektorów składa się z czterech części:

1. Dodawanie wektorów.
2. Rozkład wektorów na składowe.
3. Równowaga trzech sił.
4. Rozkład sił na równi pochyłej.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PLiOTq6ue

Interaktywny program ucząco‑monitorujący do nauki zapisu wektorów składa się z czterech części:

1. Dodawanie wektorów.

2. Rozkład wektorów na składowe.

3. Równowaga trzech sił.

4. Rozkład sił na równi pochyłej.

W dalszej części zapoznasz się z algebraicznym podejściem do wektorów ich dodawania oraz rozkładu na składowe.

Informacje ogólne

Z pojęciem wektora możesz spotkać się także w matematyce. W matematyce spotkasz się z tym, że wartość (długość) będzie częściej nazywana modułem. W matematyce też bardzo często omawia się wektory swobodne, które tym różnią się od wektorów omawianych na fizyce, że nie mają punktu przyłożenia. W dalszej części zapoznasz się z algebraicznym podejściem do dodawania wektorów oraz rozkładu wektorów na składowe na płaszczyźnie. Wektor na płaszczyźnie posiada dwie współrzędne. W przypadku zaczepienia go w początku układu współrzędnych $\left(0,0\right)$ współrzędne wektora określają wtedy punkt, w którym będzie się kończył wektor. Np. wektor o współrzędnych $\left[5;4\right]$ ma początek w punkcie $\left(0,0\right)$, a koniec w punkcie $\left(5,4\right)$. W przypadku gdy wektor rozpięty jest pomiędzy dwoma punktami jego współrzędne ustalamy poprzez odjęcie od odpowiednich współrzędnych punktu końcowego tych punktu początkowego (punktu przyłożenia). Np. gdy koniec wektora jest w punkcie o współrzędnych $\left(-7,4\right)$, a początek wektora $\left(6,7\right)$, to współrzędne wektora będą wynosiły $-7-6=-13$ oraz $4-7=-3$, zatem wektor ten będzie miał współrzędne $\left[-13;-3\right]$.

Dodawanie wektorów

Algebraiczne dodawanie wektorów polega na dodaniu do siebie odpowiednich współrzędnych każdego z wektorów. Np. $\vec{A}=\left[2;4\right]$ oraz $\vec{B}=\left[6;-8\right]$ , wtedy $\vec{A}+\vec{B}=\left[2+6;4+\left(-8\right)\right]=\left[8;-4\right]$. Dodawanie wektorów jest przemienne.

Rozkładanie wektora na składowe

Podczas rozkładu wektorów na składowe dane są równania dwóch prostych: $y=ax$ oraz $y=bx$ wektora $\vec{A}=\left[v,w\right]$. Trzeba wyznaczyć nowe proste będące przesuniętymi prostymi w stosunku do pierwotnych o wektor, w takiej sytuacji dla prostej $y=ax$ wyznaczamy wyraz wolny z pomocą równania: $d=w-av$, zatem równanie przesuniętej prostej to $y=ax+d$. Analogiczne postępowanie powtarzamy w przypadku drugiej prostej. Następnie znajdujemy punkt wspólny dla par prostych nierównoległych (przesuniętej i nieprzesuniętej) w obydwu kombinacjach. Postępowanie dla pierwszej pary: przyrównujemy równania odpowiednich prostych $ax+d=bx$ i z wyznaczamy $x$ (odciętą punktu wspólnego), następnie podstawiamy do równania jednej z przyrównanych wcześniej prostych wyznaczając rzędną punktu wspólnego ($y$). W ten sposób otrzymamy współrzędne punktu, które będą jednocześnie współrzędnymi jednego z wektorów składowych. Analogiczne postępowanie powtarzamy dla drugiej pary prostych otrzymując drugi wektor składowy. Jeśli wszystkie operacje wykonaliśmy poprawnie to suma otrzymanych wektorów jest rozkładanym wektorem.

Polecenia

3

Polecenie 2

Dodaj cztery wektory graficznie metodą równoległoboku i metodą trójkąta. Która z tych metod jest w tym wypadku szybsza?

R12a4n9AjdNZo

Szkicownik z zadaniem interaktywnym, przejdź do trybu dostępności, aby uzyskać dostosowane zadanie.

Szkicownik z zadaniem interaktywnym, przejdź do trybu dostępności, aby uzyskać dostosowane zadanie.

RegtMg6gD0C2T

(Uzupełnij).

Pokaż podpowiedź

W przypadku metody równoległoboku pamiętaj, żeby dodawać po dwa wektory na raz, a następnie dodawać wektor będący sumą poprzednich z kolejnym wektorem do dodania.
Jeśli masz problem z metodą trójkąta, skorzystaj z programu i ustaw podobne wektory i zobacz jak to zrobić.

Pokaż odpowiedź

RGwumez364oNs

Rozwiązanie metodą trójkąta.

RuBGvE3CDdMUu

Rozwiązanie metodą równoległoboku.

W przypadku dodawania większej liczby wektorów szybsza jest metoda trójkąta, gdyż umożliwia dodanie w jednym kroku wszystkich wektorów.

1

Polecenie 2

R10WbkZjSSUW0

Masz ilustracje przedstawiającą dodawanie czterech wektorów graficznie. Wektory te przedstawione są za pomocą dwóch metod: równoległoboku i trójkąta. Która z tych metod jest w tym przypadku szybsza? Wybierz poprawną odpowiedź.

Zestaw ćwiczeń interaktywnych

Słownik

Bibliografia

Sagnowska B., Szot‑Gawlik D., Godlewska M., Rozenbajgier M., Rozenbajgier R., 2017, Świat fizyki, Warszawa, WSiP.