Wielokrotności i dzielniki liczb naturalnych

Wielokrotności

RXxyR7TbY3WXI1
Animacja przedstawia wielokrotności liczb naturalnych na przykładzie obliczania wielokrotności pewnej kwoty pieniędzy.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Film dostępny pod adresem /preview/resource/RXxyR7TbY3WXI

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Animacja przedstawia wielokrotności liczb naturalnych na przykładzie obliczania wielokrotności pewnej kwoty pieniędzy.

Przykład 1

Spójrz na fragment chodniczka liczbowego. Co wspólnego mają liczby umieszczone na niebieskich polach?

RN2p2Gf9BJGC51
Animacja przedstawia za pomocą chodniczka liczbowego wielokrotności liczby 3.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Film dostępny pod adresem /preview/resource/RN2p2Gf9BJGC5

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Animacja przedstawia za pomocą chodniczka liczbowego wielokrotności liczby 3.

Ważne!

  • Liczby: 0, 3, 6, 9, … to kolejne wielokrotności liczby 3. Każda wielokrotność jest wynikiem mnożenia liczby naturalnej przez liczbę 3, np.

0·3=0,
1 ⋅ 3 = 3 ,
2·3=6.

  • Nie możemy wypisać wszystkich wielokrotności liczby 3, jest ich bowiem nieskończenie wiele.

  • Liczba zero jest najmniejszą wielokrotnością liczby 3, jak również każdej innej liczby naturalnej.

1
Ćwiczenie 1

Wypisz pięć dowolnych wielokrotności liczby

  1. 7,

  2. 12,

  3. 15,

  4. 31.

RzZoVy162CdGJ
(Uzupełnij).
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
1
Ćwiczenie 2
ROcVvUfYy5wWR
Łączenie par. Na dywaniku 100 liczb zaznacz wszystkie wielokrotności liczby 5 większe od 20, a mniejsze od 60.. 11. Możliwe odpowiedzi: 2, 3, 4, 5, 6, 7, 8, 9, 10. 21. Możliwe odpowiedzi: 2, 3, 4, 5, 6, 7, 8, 9, 10. 31. Możliwe odpowiedzi: 2, 3, 4, 5, 6, 7, 8, 9, 10. 41. Możliwe odpowiedzi: 2, 3, 4, 5, 6, 7, 8, 9, 10. 51. Możliwe odpowiedzi: 2, 3, 4, 5, 6, 7, 8, 9, 10. 61. Możliwe odpowiedzi: 2, 3, 4, 5, 6, 7, 8, 9, 10. 71. Możliwe odpowiedzi: 2, 3, 4, 5, 6, 7, 8, 9, 10. 81. Możliwe odpowiedzi: 2, 3, 4, 5, 6, 7, 8, 9, 10. 91. Możliwe odpowiedzi: 2, 3, 4, 5, 6, 7, 8, 9, 10
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RuoEiNADQ03VT
Wpisz prawidłowe liczby do poniższego zdania tak, aby było prawdziwe. Liczby wpisuj w kolejności rosnącej. Wszystkie liczby, które są wielokrotnościami liczby 5 i jednocześnie są większe od 20 i mniejsze od 60 to: Tu uzupełnij, Tu uzupełnij, Tu uzupełnij, Tu uzupełnij, Tu uzupełnij, Tu uzupełnij, Tu uzupełnij.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
2
Ćwiczenie 3
R1TfqWG4oX2eu
Współrzędne punktów zaznaczonych na osi liczbowej są wielokrotnościami liczby 23. Odczytaj współrzędne punktów A, B, C, D, E. Uzupełnij luki na osi, wpisując odpowiednie wartości.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RFPP3ne7Z4Wml
Wyobraź sobie, że wszystkie wielokrotności liczby 23 wypisano w kolejności rosnącej. Uzupełnij poniższe zdania wpisując odpowiednie wielokrotności liczby 23. Drugą wielokrotnością liczby 23 jest liczba Tu uzupełnij. Czwartą wielokrotnością liczby 23 jest liczba Tu uzupełnij. Siódmą wielokrotnością liczby 23 jest liczba Tu uzupełnij. Dziesiątą wielokrotnością liczby 23 jest liczba Tu uzupełnij. Dwunastą wielokrotnością liczby 23 jest liczba Tu uzupełnij.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RWZESrAmbhkwF2
Ćwiczenie 4
Sprawdź za pomocą kalkulatora, czy liczba 11151 jest wielokrotnością podanej liczby. Rozstrzygnij, czy zdanie jest prawdziwe, czy fałszywe. Zaznacz zdania prawdziwe. Możliwe odpowiedzi: 1. Liczba 11151 jest wielokrotnością liczby 7 , 2. Liczba 11151 jest wielokrotnością liczby 13 , 3. Liczba 11151 jest wielokrotnością liczby 11 , 4. Liczba 11151 jest wielokrotnością liczby 9

  • Liczba 11151 jest wielokrotnością liczby 7 .
  • Liczba 11151 jest wielokrotnością liczby 13 .
  • Liczba 11151 jest wielokrotnością liczby 11 .
  • Liczba 11151 jest wielokrotnością liczby 9 .
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R15rFf7bGzm4J2
Ćwiczenie 5
Wielokrotnością jakich liczb są podane liczby? Przeciągnij każdy element do odpowiedniej grupy. Wielokrotności liczby 5: Możliwe odpowiedzi: 1. 66, 2. 30, 3. 20, 4. 42, 5. 50, 6. 12, 7. 45, 8. 54, 9. 30, 10. 6, 11. 72, 12. 60, 13. 25, 14. 40, 15. 35, 16. 5, 17. 30, 18. 36, 19. 60, 20. 55, 21. 60, 22. 24, 23. 10, 24. 18, 25. 48, 26. 30, 27. 15 Wielokrotności liczby 6: Możliwe odpowiedzi: 1. 66, 2. 30, 3. 20, 4. 42, 5. 50, 6. 12, 7. 45, 8. 54, 9. 30, 10. 6, 11. 72, 12. 60, 13. 25, 14. 40, 15. 35, 16. 5, 17. 30, 18. 36, 19. 60, 20. 55, 21. 60, 22. 24, 23. 10, 24. 18, 25. 48, 26. 30, 27. 15 Wielokrotności liczby 5 oraz 6: Możliwe odpowiedzi: 1. 66, 2. 30, 3. 20, 4. 42, 5. 50, 6. 12, 7. 45, 8. 54, 9. 30, 10. 6, 11. 72, 12. 60, 13. 25, 14. 40, 15. 35, 16. 5, 17. 30, 18. 36, 19. 60, 20. 55, 21. 60, 22. 24, 23. 10, 24. 18, 25. 48, 26. 30, 27. 15 najmniejsza wspólna wielokrotność liczb 5 i 6: Możliwe odpowiedzi: 1. 66, 2. 30, 3. 20, 4. 42, 5. 50, 6. 12, 7. 45, 8. 54, 9. 30, 10. 6, 11. 72, 12. 60, 13. 25, 14. 40, 15. 35, 16. 5, 17. 30, 18. 36, 19. 60, 20. 55, 21. 60, 22. 24, 23. 10, 24. 18, 25. 48, 26. 30, 27. 15
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RPX2y3ekS2xG72
Ćwiczenie 6
Wyznacz NWW podanych liczb. Uzupełnij luki w zdaniach, wpisując odpowiednie liczby. NWW 2,3 wynosi Tu uzupełnij NWW 3,4 wynosi Tu uzupełnij NWW 5,10 wynosi Tu uzupełnij NWW 2,9 wynosi Tu uzupełnij NWW 6,8 wynosi Tu uzupełnij NWW 6,9 wynosi Tu uzupełnij
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
2
Ćwiczenie 7
R12FzmUOh51KC2
Jaką najmniejszą długość powinien mieć sznurek, aby można go było pociąć na kawałki długości 20 cm lub 25 cm? Uzupełnij lukę w odpowiedzi, wpisując poprawną wartość. Odpowiedź: Sznurek powinien mieć Tu uzupełnij cm.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
2
Ćwiczenie 8
R1F2oWFpiAw2a2
Janek i Wojtek przygotowywali się do zawodów lekkoatletycznych i biegali dookoła boiska. Wojtek przebiegał ten dystans w ciągu 5 minut, a Janek w ciągu 4 minut. Chłopcy o godzinie 14:00 wystartowali równocześnie z tego samego miejsca i pobiegli w tę samą stronę. O której godzinie spotkają się ponownie na starcie?
Uzupełnij poniższą lukę. Kliknij w nią, aby rozwinąć listę, a następnie wybierz poprawną odpowiedź. Odpowiedź: Chłopcy spotkają się na starcie o godzinie 1. 14:30, 2. 14:20, 3. 14:09.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
2
Ćwiczenie 9
R154DQYL1VdGE2
Dwa statki jednocześnie wypływają z portu. Pierwszy z nich odbywa ośmiodniowe rejsy, drugi zaś rejsy trwające 12 dni. Za ile dni statki znów spotkają się w porcie? Uzupełnij lukę w odpowiedzi, wpisując poprawną wartość. Odpowiedź: Statki spotkają się za Tu uzupełnij dni.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Dzielniki

Przykład 2

Adaś ma 6 samochodzików, które postanowił poukładać na regale, tak by na każdej półce było ich tyle samo. Pomóż Adasiowi poukładać samochodziki na półkach, na różne sposoby. Sprawdź, ile półek w regale Adaś może wykorzystać.

Rozważ:

  1. jedną półkę,

  2. dwie półki,

  3. trzy półki,

  4. cztery półki,

  5. pięć półek,

  6. sześć półek.

RjOvOWpOCmaRp1
Animacja przedstawia dzielniki liczby 6 na przykładzie ustawiania samochodzików na półkach.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

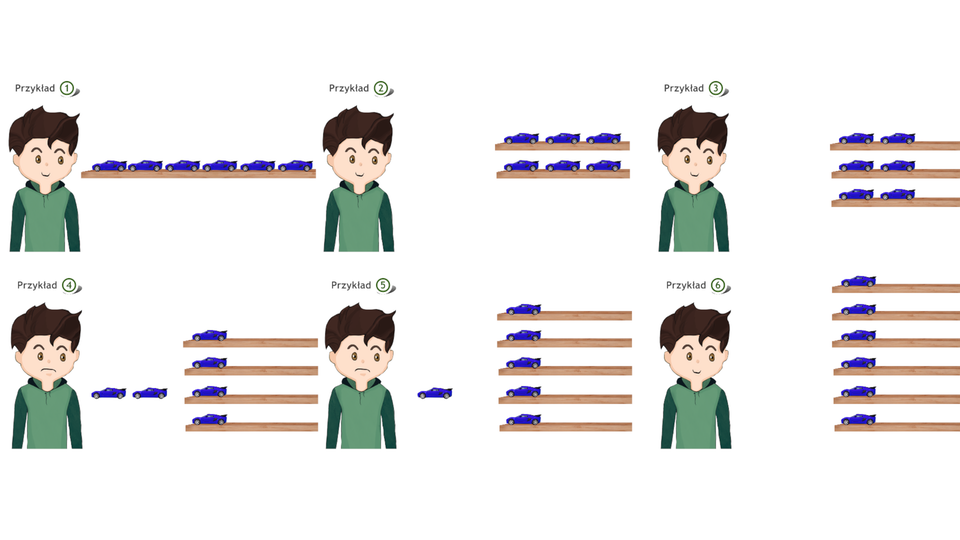
Film dostępny pod adresem /preview/resource/RjOvOWpOCmaRp

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Animacja przedstawia dzielniki liczby 6 na przykładzie ustawiania samochodzików na półkach.

Ważne!

  • Liczba 6 dzieli się bez reszty przez 1, 2, 3 i 6. Mówimy, że liczby 1, 2, 3, 6 są dzielnikami liczby 6.

  • Liczba 6 jest podzielna przez 1, 2, 3 i 6.

  • Liczba 6 nie jest podzielna przez 4 i 5, bo reszta z dzielenia nie jest równa zero.

R7mE5F5ZbonT72
Ćwiczenie 10
Poniżej przedstawiono pewne liczby oraz ich dzielniki. Połącz liczbę ze wszystkimi jej dzielnikami. 4 Możliwe odpowiedzi: 1. 1, 2, 4, 2. 1, 3, 9, 3. 1, 7, 49, 4. 1, 3, 7, 21, 5. 1, 3, 5, 15 15 Możliwe odpowiedzi: 1. 1, 2, 4, 2. 1, 3, 9, 3. 1, 7, 49, 4. 1, 3, 7, 21, 5. 1, 3, 5, 15 9 Możliwe odpowiedzi: 1. 1, 2, 4, 2. 1, 3, 9, 3. 1, 7, 49, 4. 1, 3, 7, 21, 5. 1, 3, 5, 15 21 Możliwe odpowiedzi: 1. 1, 2, 4, 2. 1, 3, 9, 3. 1, 7, 49, 4. 1, 3, 7, 21, 5. 1, 3, 5, 15 49 Możliwe odpowiedzi: 1. 1, 2, 4, 2. 1, 3, 9, 3. 1, 7, 49, 4. 1, 3, 7, 21, 5. 1, 3, 5, 15
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1ETicYGQk5fO2
Ćwiczenie 11
Wybierz odpowiedź zawierającą wszystkie dzielniki liczby 36. Zaznacz prawidłową odpowiedź. Możliwe odpowiedzi: 1. 1, 6, 12, 36, 2. 1, 3, 4, 12, 9, 36, 3. 1, 2, 3, 4, 6, 9, 12, 18, 36, 4. 1, 2, 3, 6, 9, 12, 36

  • 1 ,   6 ,   12 ,   36
  • 1 ,   3 ,   4 ,   12 ,   9 ,   36
  • 1 ,   2 ,   3 ,   4 ,   6 ,   9 ,   12 ,   18 ,   36
  • 1 ,   2 ,   3 ,   6 ,   9 ,   12 ,   36
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
2
Ćwiczenie 12
RvbghDXtwZ5m52
Poniżej przedstawiono dzielniki pewnych liczb. Jakie to liczby? Uzupełnij puste miejsca w poniższych stwierdzeniach, wpisując najmniejszą liczbę podzielną przez podane dzielniki. Liczba której wszystkimi dzielnikami są 1, 2, 5, 10 to Tu uzupełnij.Liczba której wszystkimi dzielnikami są 1, 2, 3, 6, 9, 18 to Tu uzupełnij. Liczba której wszystkimi dzielnikami są 1, 2, 4, 13, 26, 52 to Tu uzupełnij. Liczba której wszystkimi dzielnikami są 1, 2, 3, 5, 6, 10, 15, 30 to Tu uzupełnij.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RppQiZCgY2Fgr2
Ćwiczenie 13
Rozstrzygnij, czy zdanie jest prawdziwe, czy fałszywe. Zaznacz prawidłowe odpowiedzi. Możliwe odpowiedzi: 1. Liczba 1 jest dzielnikiem każdej liczby., 2. Każda liczba, różna od zera, jest swoim dzielnikiem., 3. Liczba 2 jest dzielnikiem każdej liczby parzystej., 4. Każda liczba, różna od zera, jest dzielnikiem zera., 5. Każda liczba ma przynajmniej dwa dzielniki., 6. Liczba 3 jest dzielnikiem każdej liczby nieparzystej.

  • Liczba 1 jest dzielnikiem każdej liczby.
  • Każda liczba, różna od zera, jest swoim dzielnikiem.
  • Liczba 2 jest dzielnikiem każdej liczby parzystej.
  • Każda liczba, różna od zera, jest dzielnikiem zera.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1JFHRnYfNg1w2
Ćwiczenie 14
Które z podanych iloczynów są podzielne przez 9? Zaznacz prawidłowe odpowiedzi. Możliwe odpowiedzi: 1. 9·4·25, 2. 18·6·4, 3. 25·5·4, 4. 27·21·7

  • 9 ∙ 4 ∙ 25
  • 18 ∙   6   ∙   4
  • 25 ∙ 5   ∙ 4
  • 27 ∙   21   ∙   7
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Dzielniki – zadania

R1LyMJm2NatO12
Ćwiczenie 15
Znajdź dzielniki poniższych liczb, a następnie uzupełnij luki. Kliknij w nie, aby rozwinąć listę, a następnie wybierz poprawną odpowiedź. Liczby uporządkuj w kolejności rosnącej. Wszystkie dzielniki liczby 15.
1. 15, 2. 5, 3. 3, 4. 1, 5. 5, 6. 15, 7. 15, 8. 10, 9. 5, 10. 3, 11. 1, 12. 9, 13. 45, 14. 1, 15. 3, 16. 15, 17. 30, 18. 35, 1. 15, 2. 5, 3. 3, 4. 1, 5. 5, 6. 15, 7. 15, 8. 10, 9. 5, 10. 3, 11. 1, 12. 9, 13. 45, 14. 1, 15. 3, 16. 15, 17. 30, 18. 35, 1. 15, 2. 5, 3. 3, 4. 1, 5. 5, 6. 15, 7. 15, 8. 10, 9. 5, 10. 3, 11. 1, 12. 9, 13. 45, 14. 1, 15. 3, 16. 15, 17. 30, 18. 35, 1. 15, 2. 5, 3. 3, 4. 1, 5. 5, 6. 15, 7. 15, 8. 10, 9. 5, 10. 3, 11. 1, 12. 9, 13. 45, 14. 1, 15. 3, 16. 15, 17. 30, 18. 35Wszystkie dzielniki liczby 45.
1. 15, 2. 5, 3. 3, 4. 1, 5. 5, 6. 15, 7. 15, 8. 10, 9. 5, 10. 3, 11. 1, 12. 9, 13. 45, 14. 1, 15. 3, 16. 15, 17. 30, 18. 35, 1. 15, 2. 5, 3. 3, 4. 1, 5. 5, 6. 15, 7. 15, 8. 10, 9. 5, 10. 3, 11. 1, 12. 9, 13. 45, 14. 1, 15. 3, 16. 15, 17. 30, 18. 35, 1. 15, 2. 5, 3. 3, 4. 1, 5. 5, 6. 15, 7. 15, 8. 10, 9. 5, 10. 3, 11. 1, 12. 9, 13. 45, 14. 1, 15. 3, 16. 15, 17. 30, 18. 35,1. 15, 2. 5, 3. 3, 4. 1, 5. 5, 6. 15, 7. 15, 8. 10, 9. 5, 10. 3, 11. 1, 12. 9, 13. 45, 14. 1, 15. 3, 16. 15, 17. 30, 18. 35, 1. 15, 2. 5, 3. 3, 4. 1, 5. 5, 6. 15, 7. 15, 8. 10, 9. 5, 10. 3, 11. 1, 12. 9, 13. 45, 14. 1, 15. 3, 16. 15, 17. 30, 18. 35, 1. 15, 2. 5, 3. 3, 4. 1, 5. 5, 6. 15, 7. 15, 8. 10, 9. 5, 10. 3, 11. 1, 12. 9, 13. 45, 14. 1, 15. 3, 16. 15, 17. 30, 18. 35Wszystkie wspólne dzielniki liczb 15 i 45.
1. 15, 2. 5, 3. 3, 4. 1, 5. 5, 6. 15, 7. 15, 8. 10, 9. 5, 10. 3, 11. 1, 12. 9, 13. 45, 14. 1, 15. 3, 16. 15, 17. 30, 18. 35, 1. 15, 2. 5, 3. 3, 4. 1, 5. 5, 6. 15, 7. 15, 8. 10, 9. 5, 10. 3, 11. 1, 12. 9, 13. 45, 14. 1, 15. 3, 16. 15, 17. 30, 18. 35, 1. 15, 2. 5, 3. 3, 4. 1, 5. 5, 6. 15, 7. 15, 8. 10, 9. 5, 10. 3, 11. 1, 12. 9, 13. 45, 14. 1, 15. 3, 16. 15, 17. 30, 18. 35, 1. 15, 2. 5, 3. 3, 4. 1, 5. 5, 6. 15, 7. 15, 8. 10, 9. 5, 10. 3, 11. 1, 12. 9, 13. 45, 14. 1, 15. 3, 16. 15, 17. 30, 18. 35Największy wspólny dzielnik liczb 15 i 45
1. 15, 2. 5, 3. 3, 4. 1, 5. 5, 6. 15, 7. 15, 8. 10, 9. 5, 10. 3, 11. 1, 12. 9, 13. 45, 14. 1, 15. 3, 16. 15, 17. 30, 18. 35.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RlfnrJboLbSf03
Ćwiczenie 16
Wyznacz NWD podanych liczb. Uzupełnij puste miejsca. NWD 12,3 wynosi Tu uzupełnij NWD 8,10 wynosi Tu uzupełnij NWD 5,10 wynosi Tu uzupełnij NWD 6,18 wynosi Tu uzupełnij NWD 10,15 wynosi Tu uzupełnij NWD 18,27 wynosi Tu uzupełnij
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
3
Ćwiczenie 17
RHfVMoYDGT1Aa3
Ania ma 18 cukierków i 12 ciasteczek. Ilu najwięcej gości może zaprosić, aby każdy z uczestników przyjęcia, łącznie z Anią, otrzymał po tyle samo słodyczy? Uzupełnij lukę w zdaniu, wpisując poprawną wartość. Odpowiedź: Ania może zaprosić Tu uzupełnij osób.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R7gFbTbyxAwdW3
Ćwiczenie 18
Wypisz wszystkie dzielniki liczby 28. Uzupełnij puste pole wpisując liczbę będącą sumą wszystkich dzielników z wyjątkiem największego. Odpowiedź: Suma wszystkich dzielników z wyjątkiem największego wynosi Tu uzupełnij.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ciekawostka

Liczba 28 jest liczbą doskonałą.

Liczba jest doskonała, gdy jest równa sumie swoich dzielników właściwych (tj. wszystkich dzielników naturalnych mniejszych od niej samej).

RjS5czUSjI7sm3
Ćwiczenie 19
Znajdź inną liczbę doskonałą, mniejszą od 10. Uzupełnij puste pole wpisując liczbę. Odpowiedź: Liczba doskonała mniejsza od to Tu uzupełnij.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
3
Polecenie 1

Poszukaj informacji, ile jest liczb doskonałych mniejszych od 1000. Jakie to liczby?

RziVJUgtIYd4C
(Uzupełnij).