Własności dwusiecznej kąta
Złożymy odpowiednio kwadratową kartkę papieru, a następnie rozprostujemy ją.
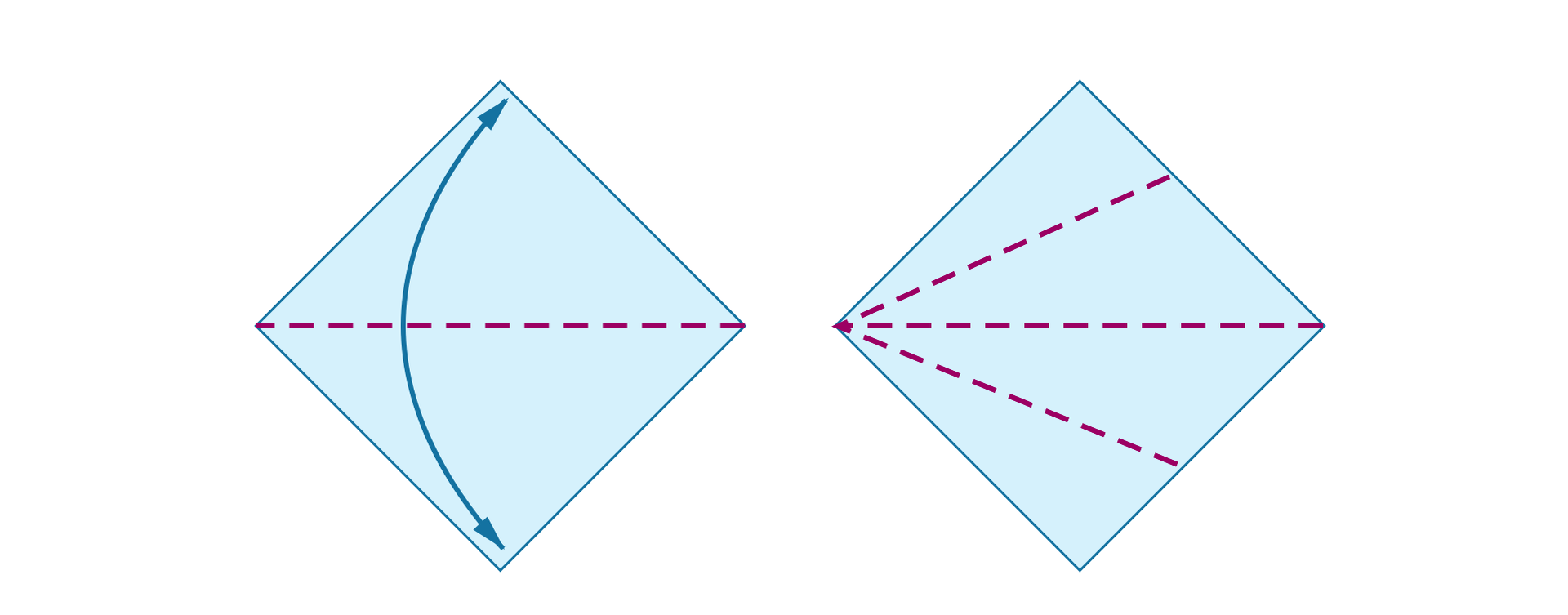
Ślady zgięć, dzielą niektóre kąty kwadratu na dwie przystające części. Ślady te możemy uznać za modele półprostych, zwanych dwusiecznymi.
Co to są dwusieczne i jakie mają własności – dowiesz się, analizując przykłady zawarte w tym materiale.
Interaktywna treść merytorycznaInteraktywna treść merytoryczna
AnimacjaAnimacja
Zestaw ćwiczeń interaktywnychZestaw ćwiczeń interaktywnych
SłownikSłownik
Rozpoznasz dwusieczną kąta.
Skonstruujesz dwusieczną kąta.
We wnętrzu kąta wskażesz punkty równoodległe od każdego z ramion.
Zastosujesz własności dwusiecznej w zadaniach geometrycznych.
Zaopatrz się w linijkę oraz cyrkiel i postępuj według instrukcji.
Co musisz zrobić | Co otrzymasz |
|---|---|
Narysuj kąt . | 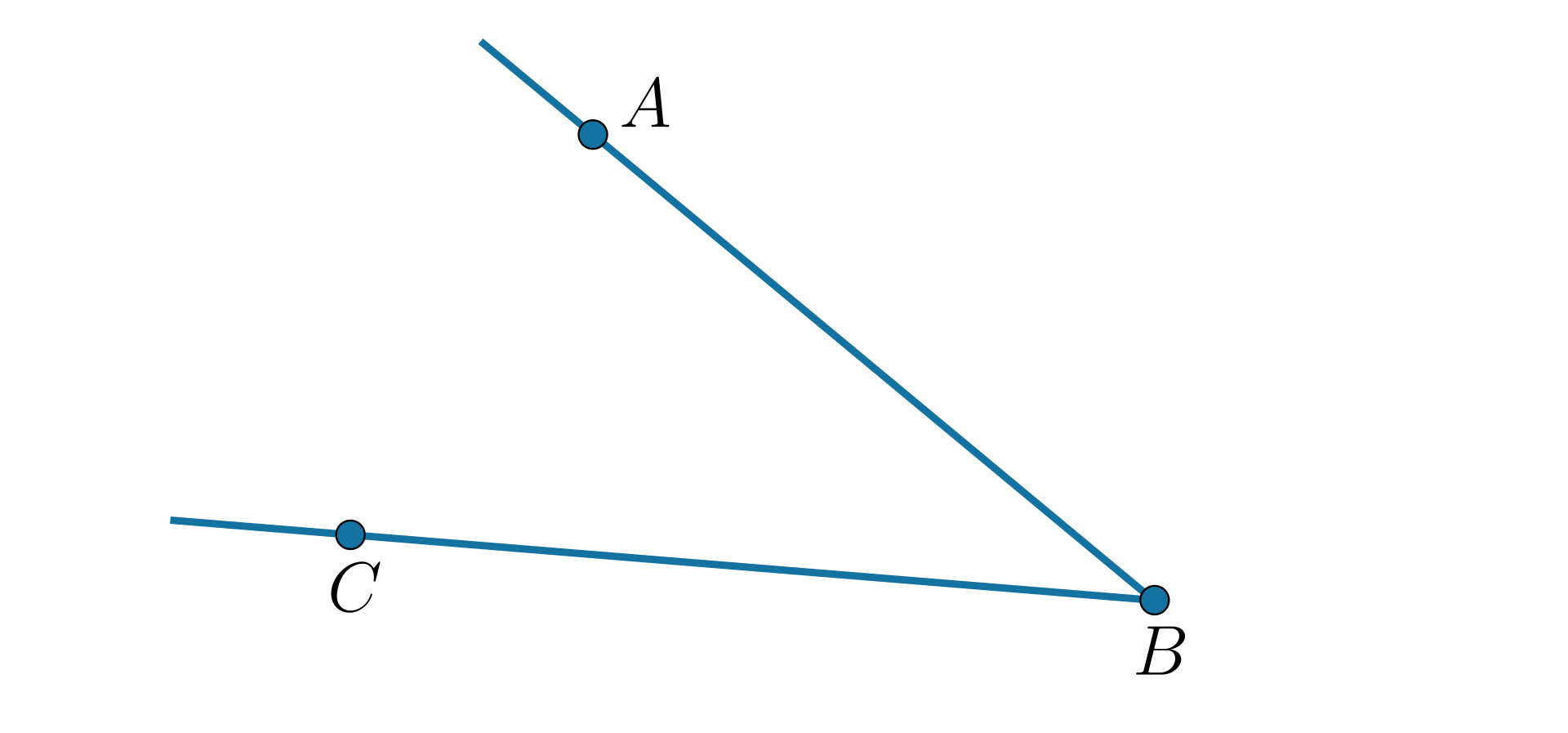 Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0. |
Z wierzchołka kąta zakreśl cyrklem łuk przecinający ramiona kąta. | 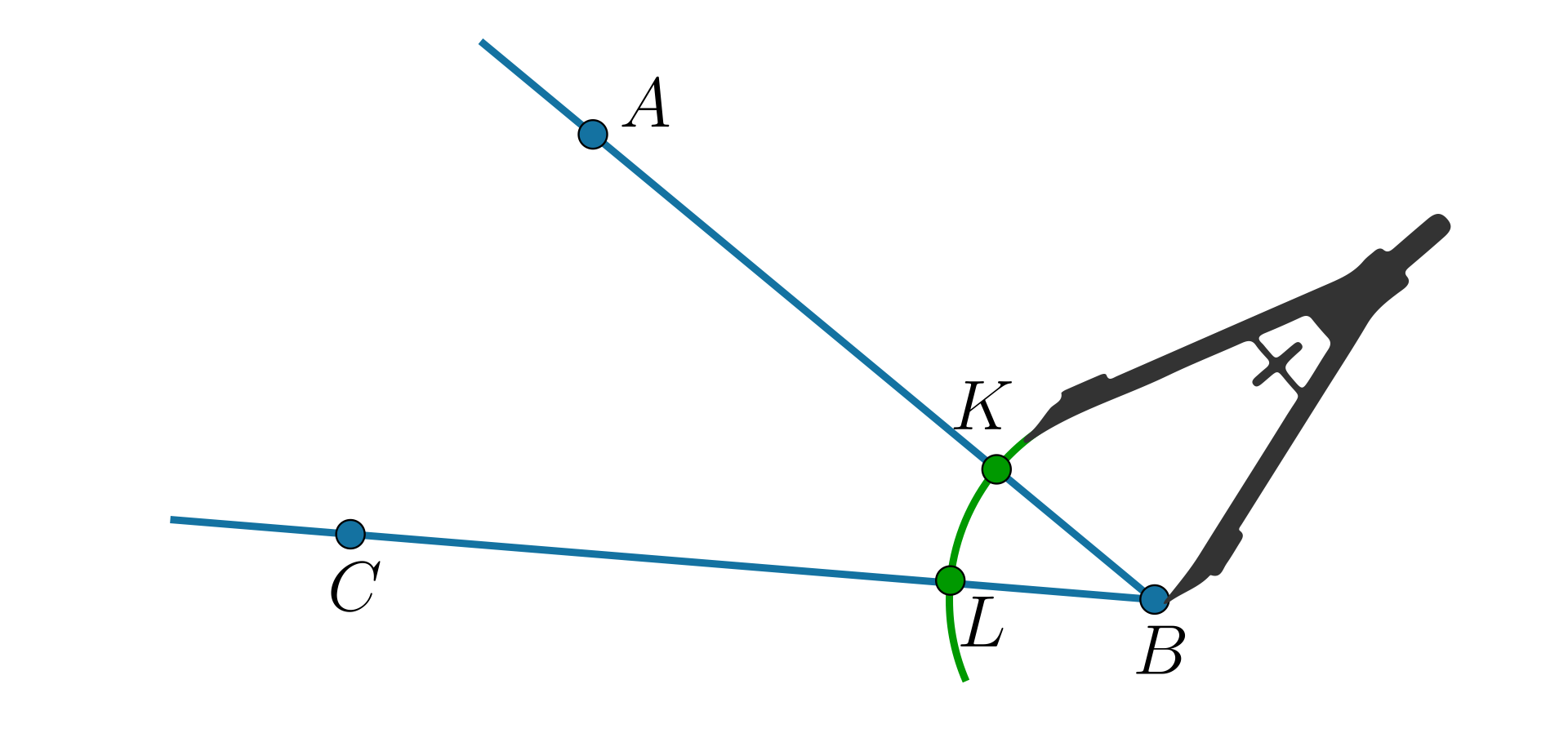 Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0. |
Z punktów i tą samą rozwartością cyrkla zakreśl dwa łuki tak, aby łuki przecięły się w punkcie leżącym wewnątrz kąta. Punkt przecięcia oznacz przez . | 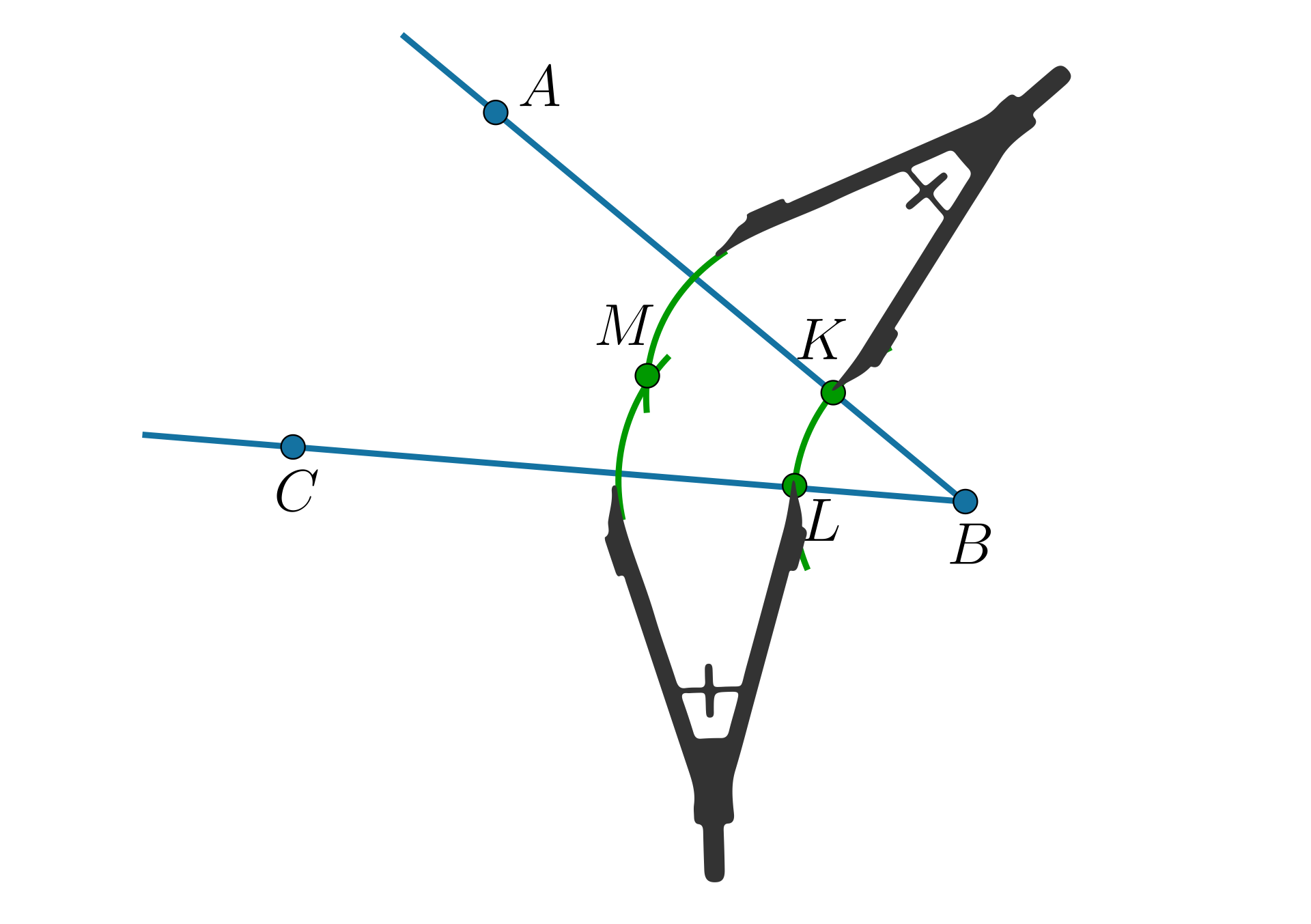 Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0. |
Narysuj półprostą . | 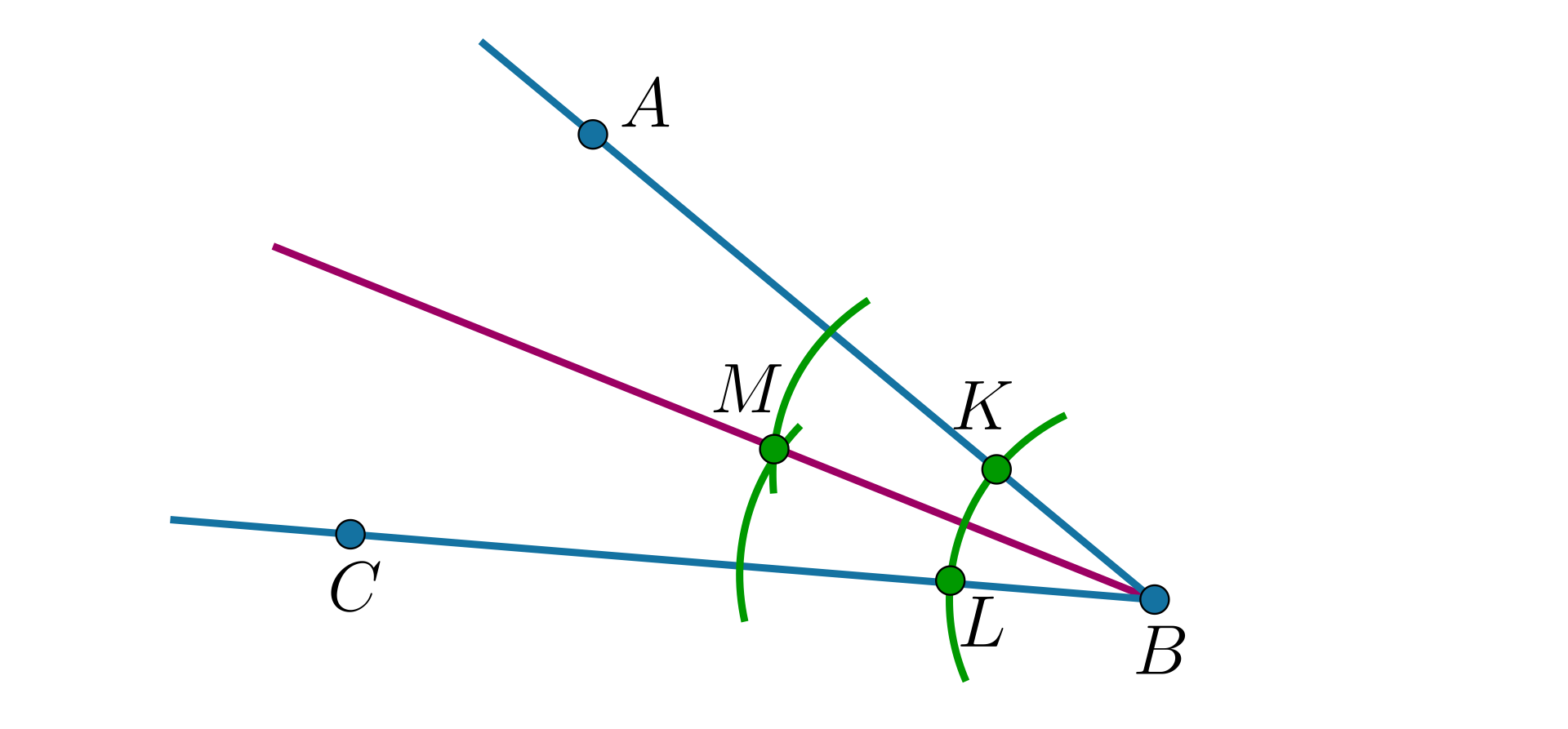 Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0. |
Półprosta, otrzymana w wyniku konstrukcji dzieli kąt na dwie równe części. O takiej półprostej powiemy, że jest dwusieczną kątadwusieczną kąta .
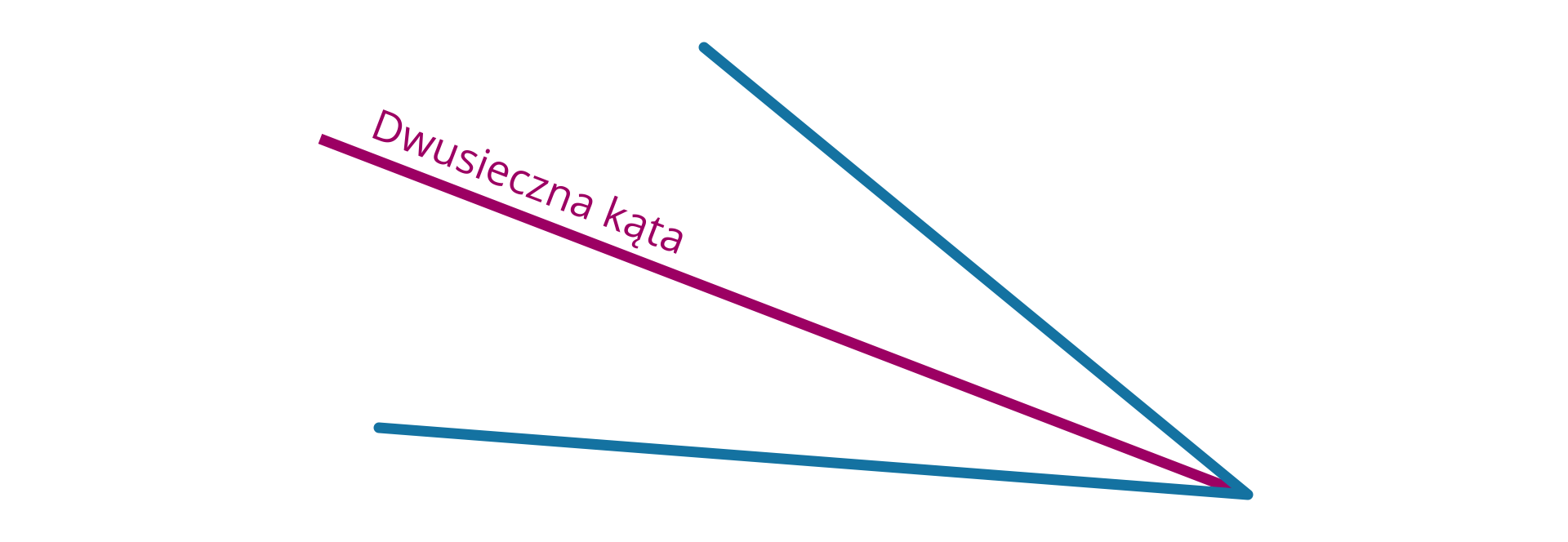
Dwusieczną kątaDwusieczną kąta nazywamy półprostą o początku w wierzchołku tego kąta, dzielącą kąt na dwa kąty równe.
Narysujemy dwa kąty wierzchołkowe, a następnie zaznaczymy dwusieczne tych kątów.
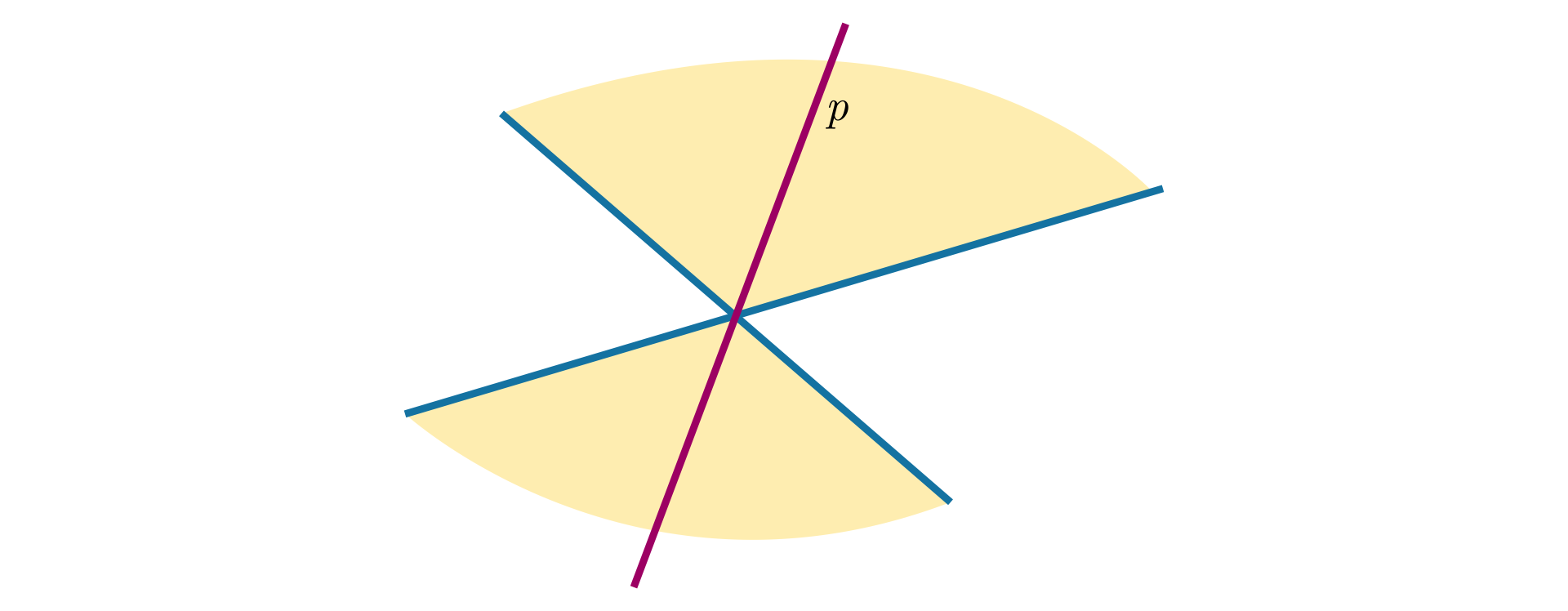
Zauważmy, że dwusieczne kątów wierzchołkowych tworzą prostą.
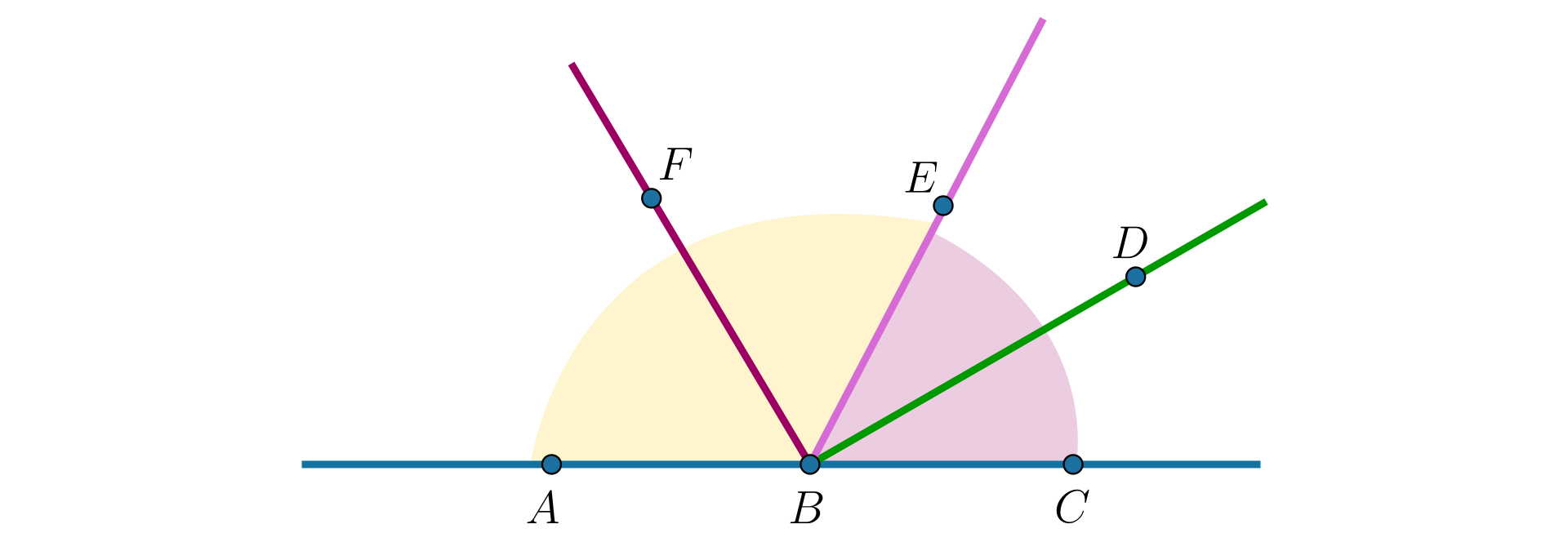
Określimy, jaki kąt tworzą dwusieczne kątów przyległych i .
Narysujemy te kąty i ich dwusieczne - odpowiednio i (patrz rysunek).
Oznaczmy:
– miara kąta ,
– miara kąta .
Dwusieczna dzieli każdy z kątów na połowy.
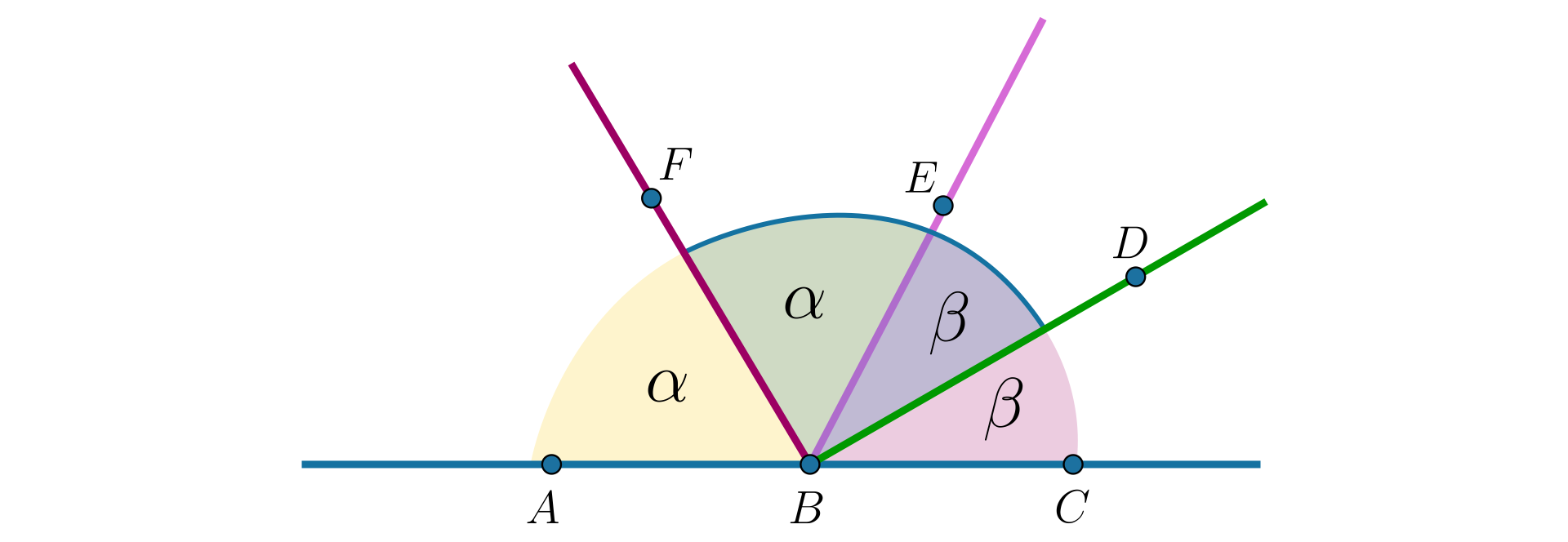
Miara kąta między dwusiecznymi jest równa .
Suma miar kątów przyległych jest równa , zatem:
.
Czyli:
Wniosek
Dwusieczne kątów przyległych tworzą kąt prosty.
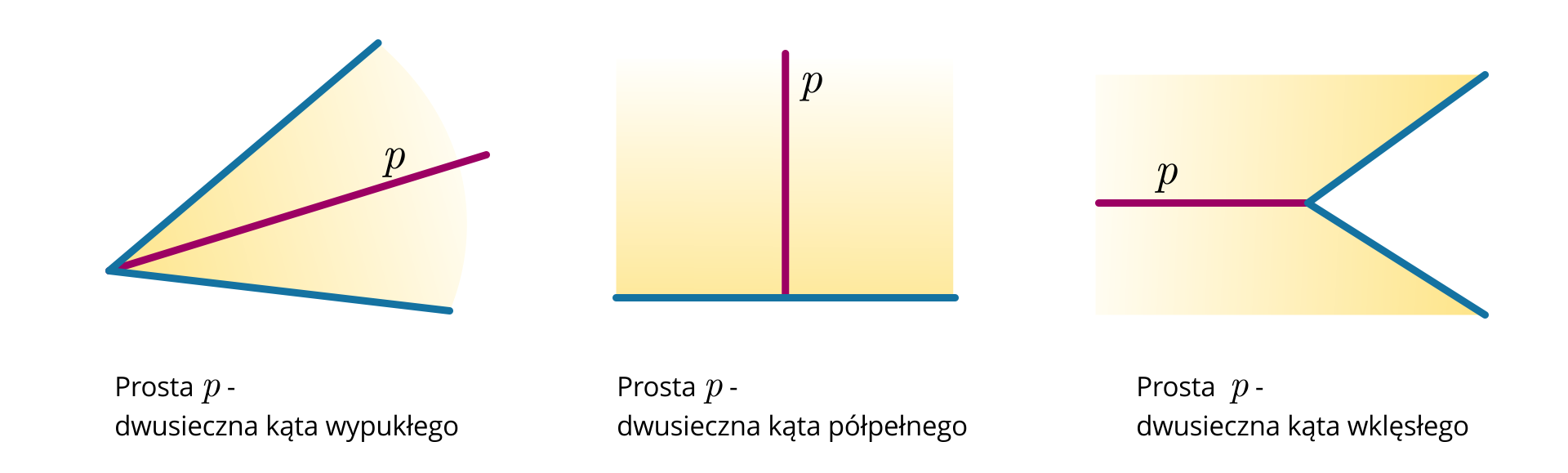
Dwusieczna kątaDwusieczna kąta wypukłego (różnego od kąta półpełnego) należy do wnętrza tego kąta i jest zbiorem punktów równo odległych od ramion tego kąta.
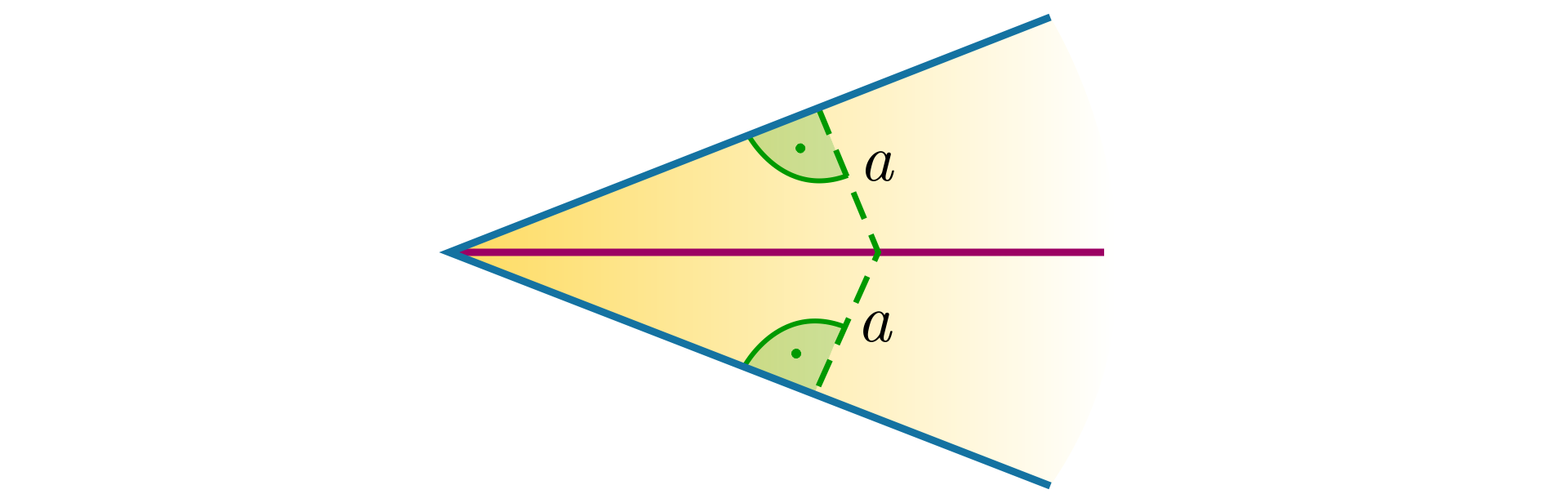
Każdy punkt kąta wypukłego równo odległy od ramion kąta leży na dwusiecznej tego kąta.
Punkt leży na dwusiecznej kąta . Miara kąta jest równa . Obliczymy miary kątów czworokąta .
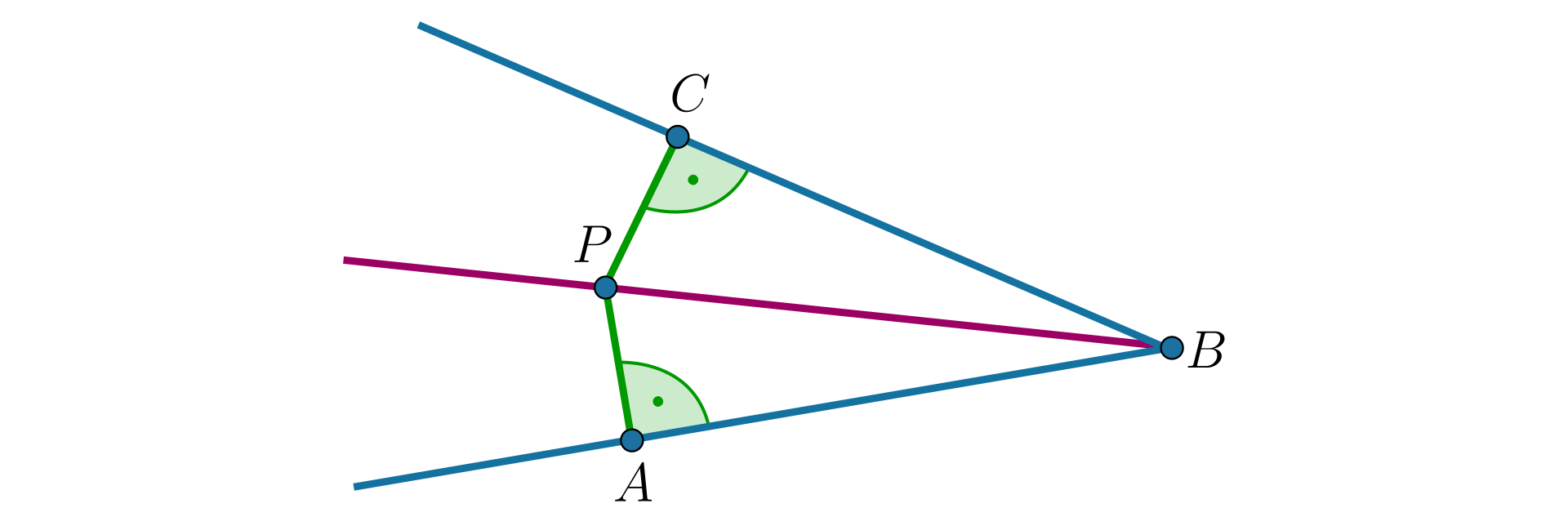
Rozważmy najpierw trójkąt . Jest to trójkąt prostokątny, w którym kąt ostry ma miarę . Zatem
Półprosta jest dwusieczną kątadwusieczną kąta , więc
Kąt jest sumą kątów i , zatem
Trókąt jest prostokątny i jeden z jego kątów ostrych ma miarę .
Drugi z kątów tego trójkąta jest więc równy:
Możemy już obliczyć miarę kąta .
Kąty czworokąta są równe: , , , .
Uwaga – miary kątów czworokąta można też obliczyć, korzystając z przystawania trójkątów i .
W trójkącie równoramiennym , w którym , poprowadzono dwusieczną . Wykażemy, że ta dwusieczna jest środkową i zarazem wysokością tego trójkąta.
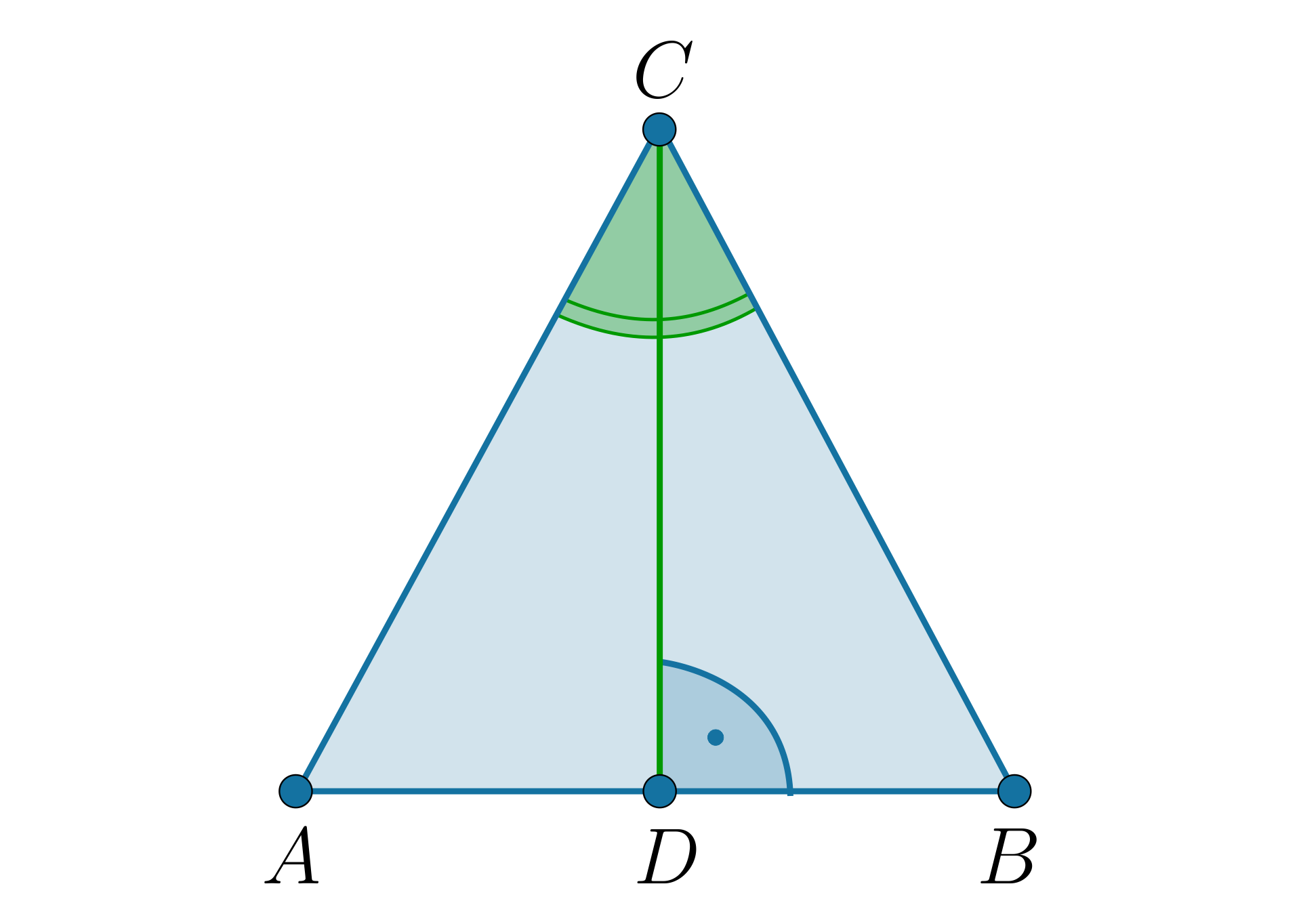
Zauważmy najpierw, że trójkąty i są przystające, bowiem:
– ramiona trójkąta równoramiennego
– bok wspólny trójkątów
– kąty utworzone przez dwusieczną
Na mocy cech przystawania trójkątów trójkąty i są przystające.
Z przystawania tych trójkątów wynika, że , czyli to środkowa trójkąta .
Punkt leży na prostej , więc .
Stąd:Z przystawania trójkątów i wynika, że
Zatem
Czyli dwusieczna jest też wysokością trójkąta , co należało wykazać.
Bok trójkąta równobocznego jest równy . Dwusieczna kątaDwusieczna kąta przecina bok w punkcie . Obliczymy długość odcinka .
W trójkącie równobocznym dwusieczna jest zarazem wysokością. Skorzystamy więc ze wzoru na wysokość trójkąta równobocznego.
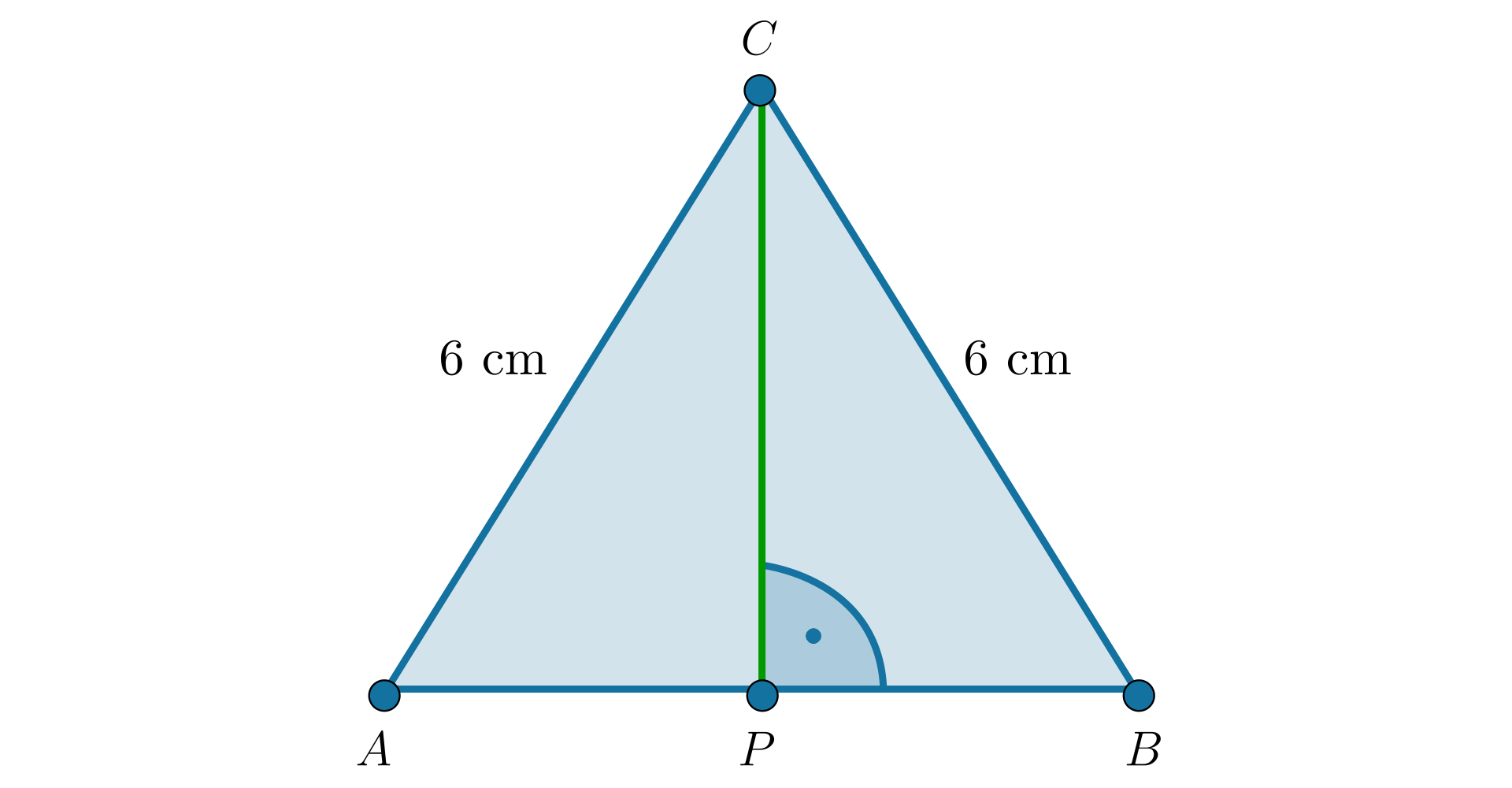
Długość odcinka jest równa .
W trójkącie poprowadzono dwusieczne kątów i . Dwusieczne te przecięły się w punkcie . Przez punkt poprowadzono prostą równoległą do boku , która przecięła bok w punkcie , natomiast bok w punkcie .
Wykażemy, że
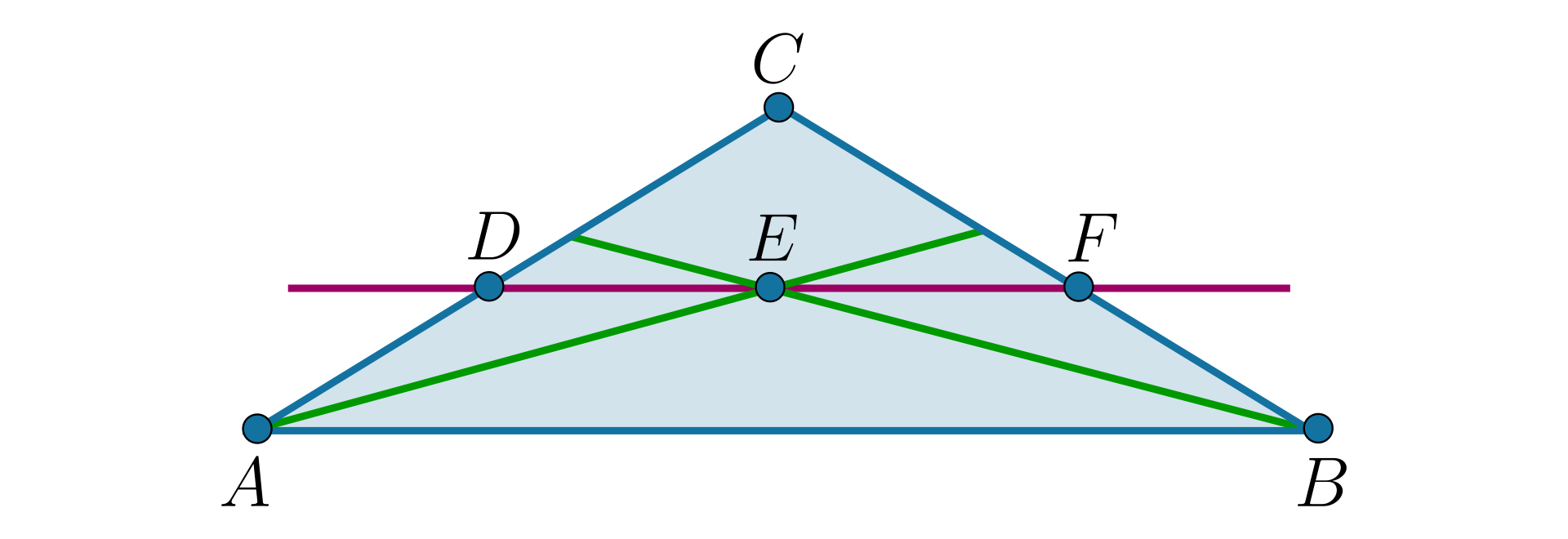
Proste i są równoległe, kąty i są więc kątami naprzemianległymi, zatem
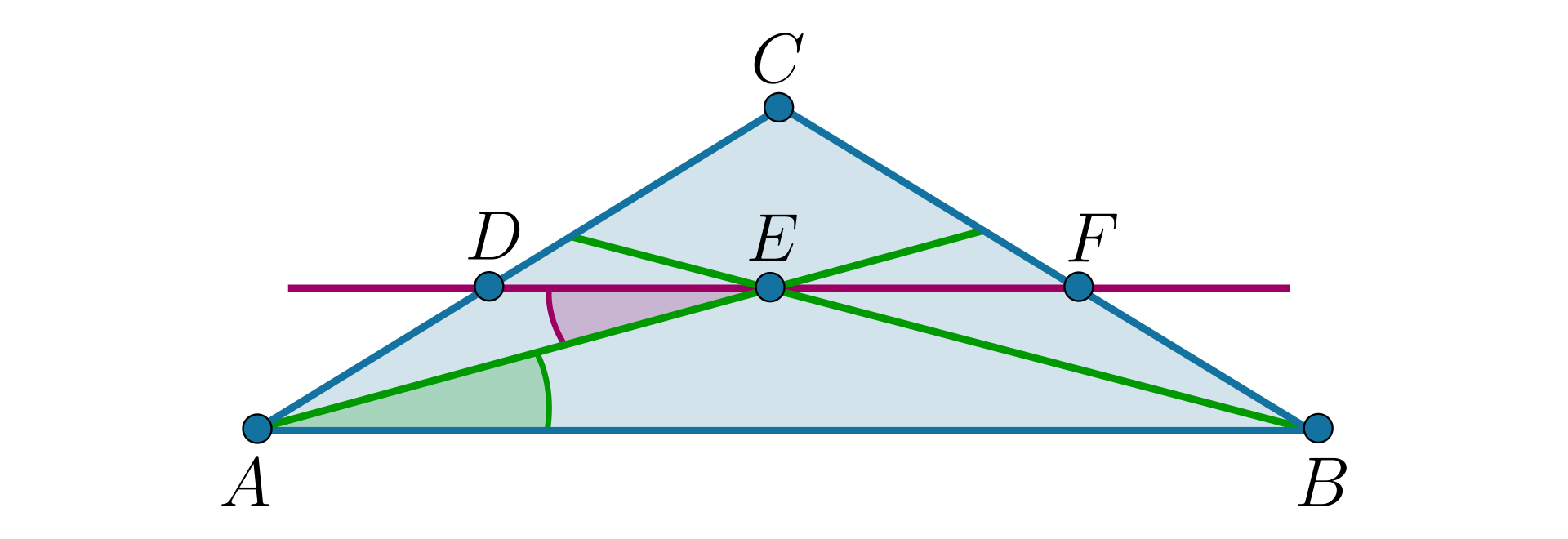
Prosta jest dwusieczną kątadwusieczną kąta , więc .
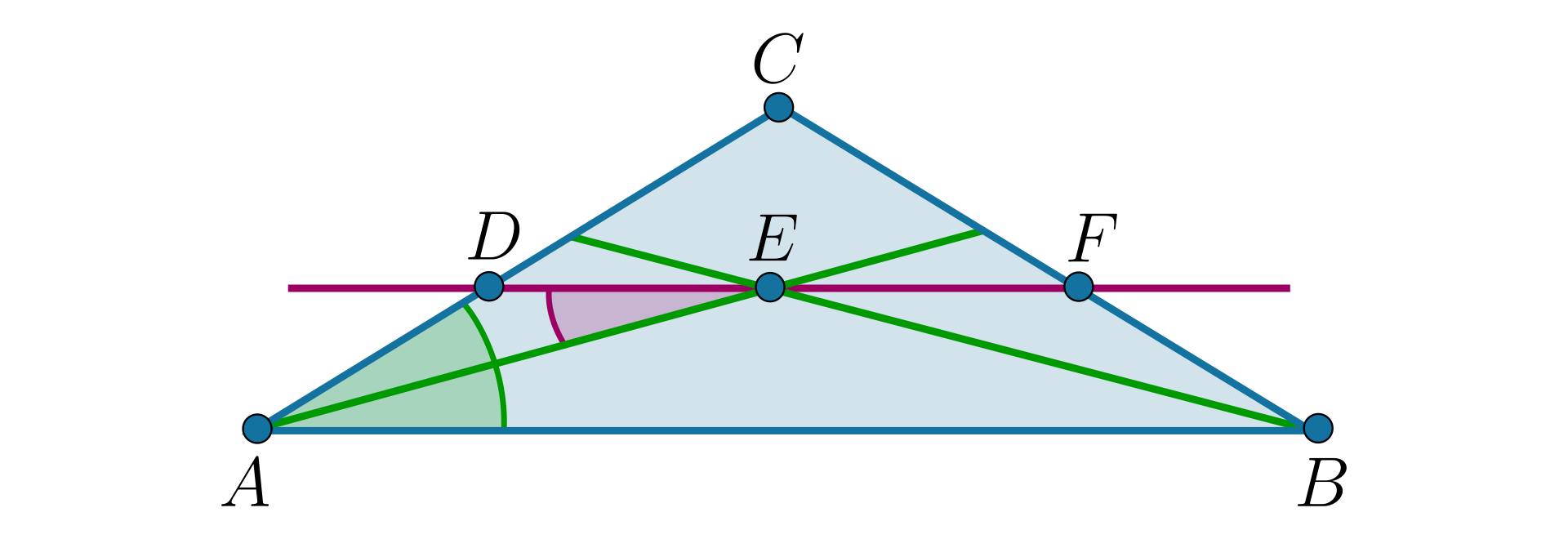
Wynika stąd, że trójkąt jest równoramienny (ma dwa równe kąty).
Zatem .
W podobny sposób możemy wykazać, że trójkąt jest równoramienny i .
Stąd:
,
co należało wykazać.
Notatnik
Animacja
Zapoznaj się z animacją. Poznasz ciekawe własności dwusiecznych kątów w wielokątach.
Rozwiąż najpierw samodzielnie zamieszczone w animacji zadania i dopiero wtedy porównaj z proponowanymi rozwiązaniami.

Film dostępny pod adresem /preview/resource/R1EXgOUp5jCrB
Film prezentuje zastosowanie własności dwusiecznej kąta.
W trapezie , w którym , poprowadzono dwusieczne kątów i . Dwusieczne te przecięły się w punkcie . Wiedząc, że i , oblicz obwód trójkąta .
W trójkącie równoramiennym kąt między ramionami i jest równy
. Oblicz, pod jakim kątem ostrym przecinają się dwusieczne kątów i .
W trójkącie równobocznym dwusieczna kąta przecina bok w punkcie . Oblicz obwód trójkąta , jeżeli obwód trójkąta jest równy .
Zestaw ćwiczeń interaktywnych
Dwusieczna kątów leżących przy tym samym ramieniu trapezu przecinają się pod kątem 1. prostym, 2. prostym, 3. prostym, 4. rozwartym, 5. prostym, 6. rozwartym.
W trójkącie równobocznym dwusieczne kątów i przecinają się w punkcie . Zatem kąt jest kątem 1. prostym, 2. prostym, 3. prostym, 4. rozwartym, 5. prostym, 6. rozwartym.
Dwusieczne kątów rombu przecinają się pod katem 1. prostym, 2. prostym, 3. prostym, 4. rozwartym, 5. prostym, 6. rozwartym.
W trójkącie prostokątnym równoramiennym , na przeciwprostokątnej obrano punkt , który leży w tej samej odległości od każdej z przyprostokątnych. Przyprostokątna tego trójkąta ma długość . Oblicz pole trójkąta .
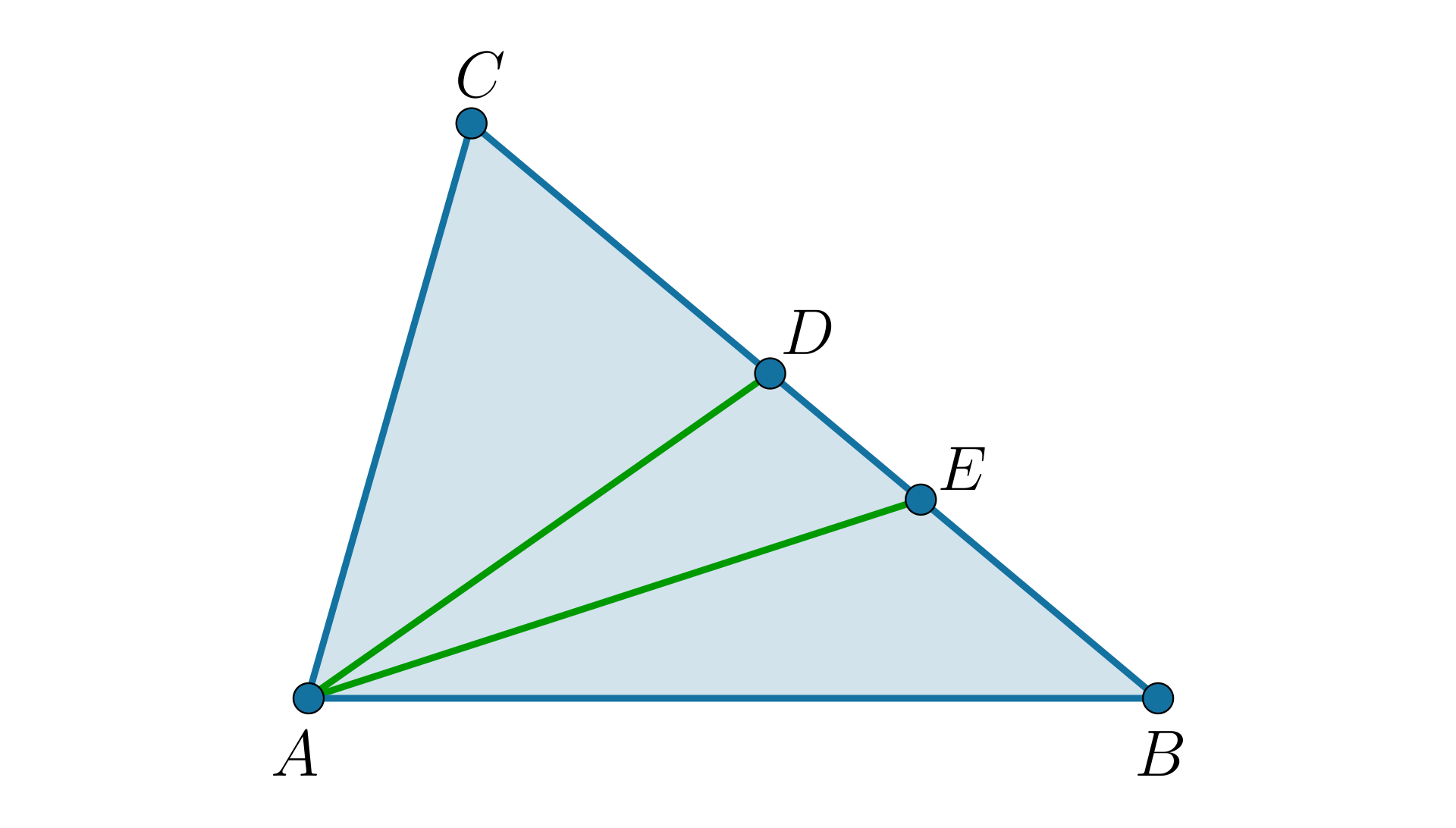
W trójkącie na boku zaznaczono punkt taki, że kąty i są równe. Dwusieczna kąta przecina bok w punkcie . Wykaż, że .
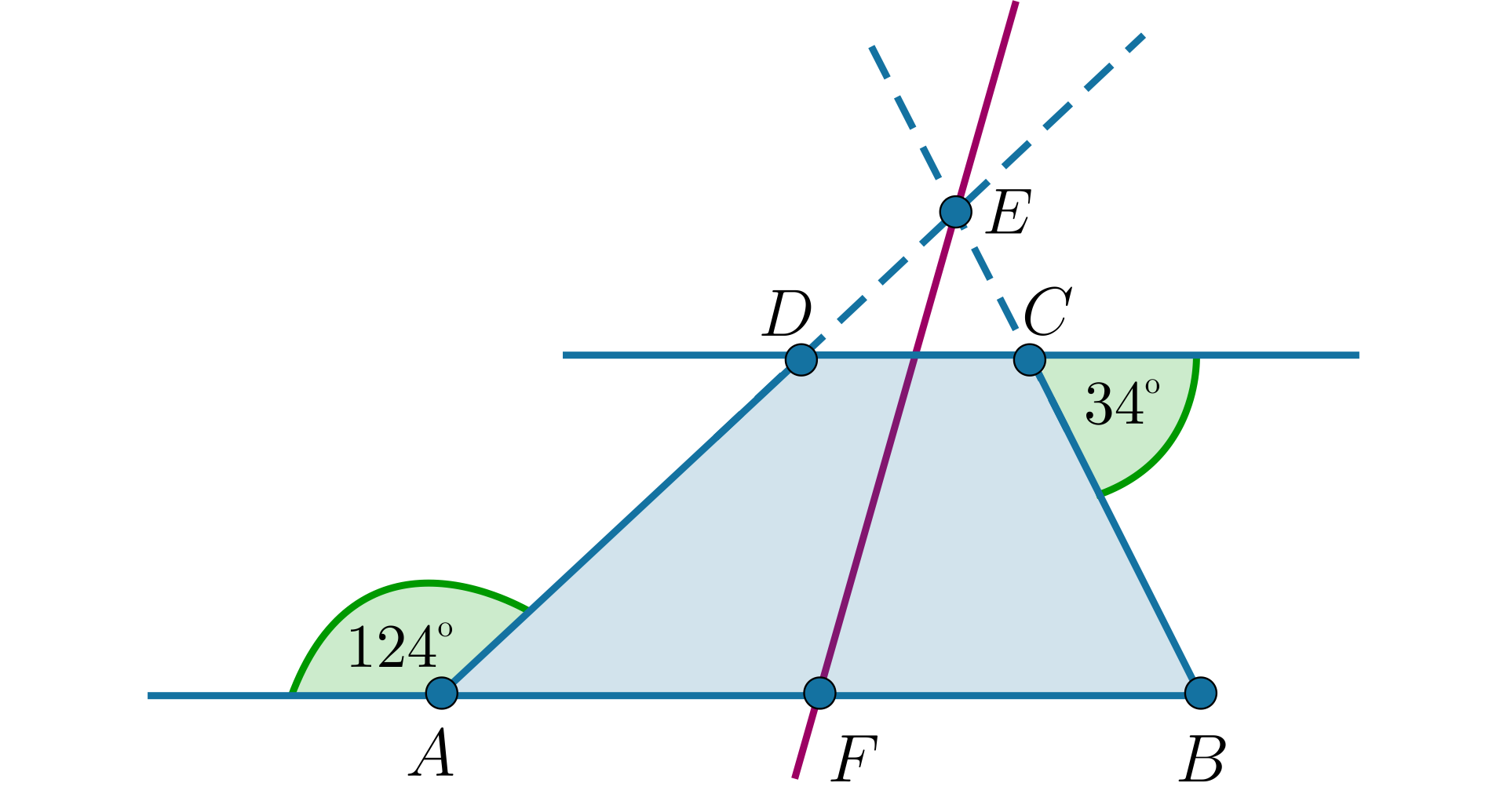
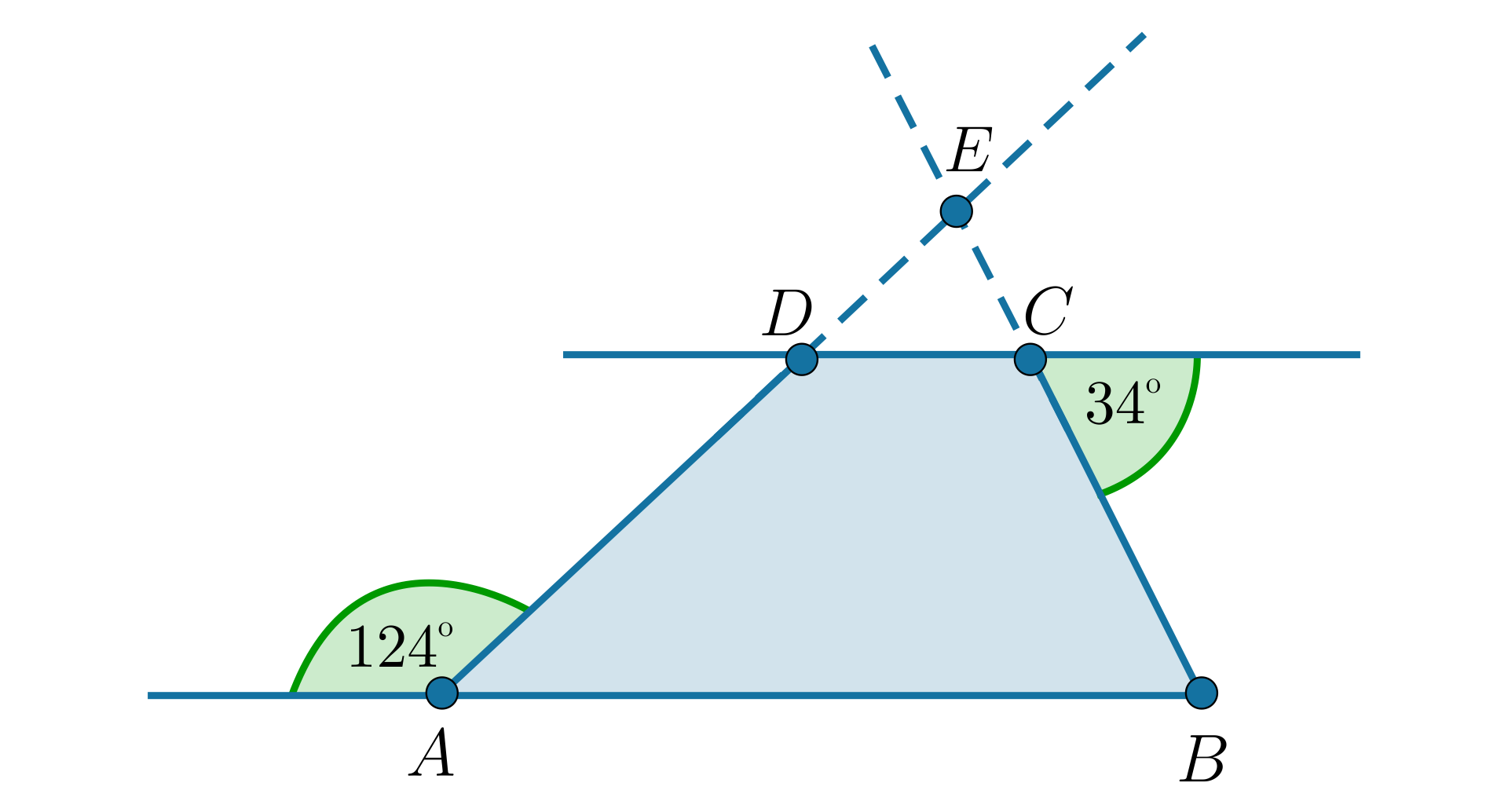
W trapezie przedłużono ramiona aż do przecięcia w punkcie . Wykaż, że dwusieczna kąta tworzy z bokiem kąt . Przyjmij oznaczenia jak na poniższym rysunku.
Słownik
półprosta o początku w wierzchołku tego kąta, dzielącą kąt na dwa kąty równe.
Bibliografia
Zarzycki P., (2007), Wszystkie twierdzenia duże i małe, Opole: Wydawnictwo NOWIK.