Wykres funkcji f(x)=a/x
W tym materiale zajmiemy się funkcjami opisanymi takim samym wzorem jak proporcjonalność odwrotna, czyli , ale określonymi dla dowolnej liczby . Przyjmiemy, że współczynnik .
Zastanówmy się, jak wygląda wykres tej funkcji.
Odczytaj z wykresu lub oblicz na podstawie wzoru jakie wartości przyjmuje funkcja dla podanych argumentów. Aby sprawdzić swoją odpowiedź, wpisz w puste pole wyznaczoną wartość funkcji oraz naciśnij przycisk.
Zapoznaj się z opisem poniższego apletu i oblicz na podstawie wzoru jakie wartości przyjmuje funkcja dla różnych argumentów.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/Pbfh3SsUp
Wykres znajdujący się w powyższym przykładzie nazywamy hiperbolą. Ta hiperbola składa się z dwóch ramion położonych symetrycznie względem punktu . Charakterystyczne dla tego wykresu jest to, że każde z jego ramion zbliża się do osi układu współrzędnych, ale w żadnym punkcie nie przecina ani osi , ani .
Przyjrzymy się innym własnościom funkcji .
Odczytaj z wykresu własności funkcji .

Ramiona hiperboli leżą w i ćwiartce układu współrzędnych.
Funkcja jest określona dla wszystkich (wykres funkcji nie przecina
osi ).Zbiorem wartości jest przedział .
Funkcja nie ma miejsc zerowych (wykres funkcji nie ma punktów wspólnych z osią ).
Funkcja jest malejąca w każdym z przedziałów oraz .
Funkcja przyjmuje wartości dodatnie dla argumentów z przedziału oraz wartości ujemne dla argumentów z przedziału .
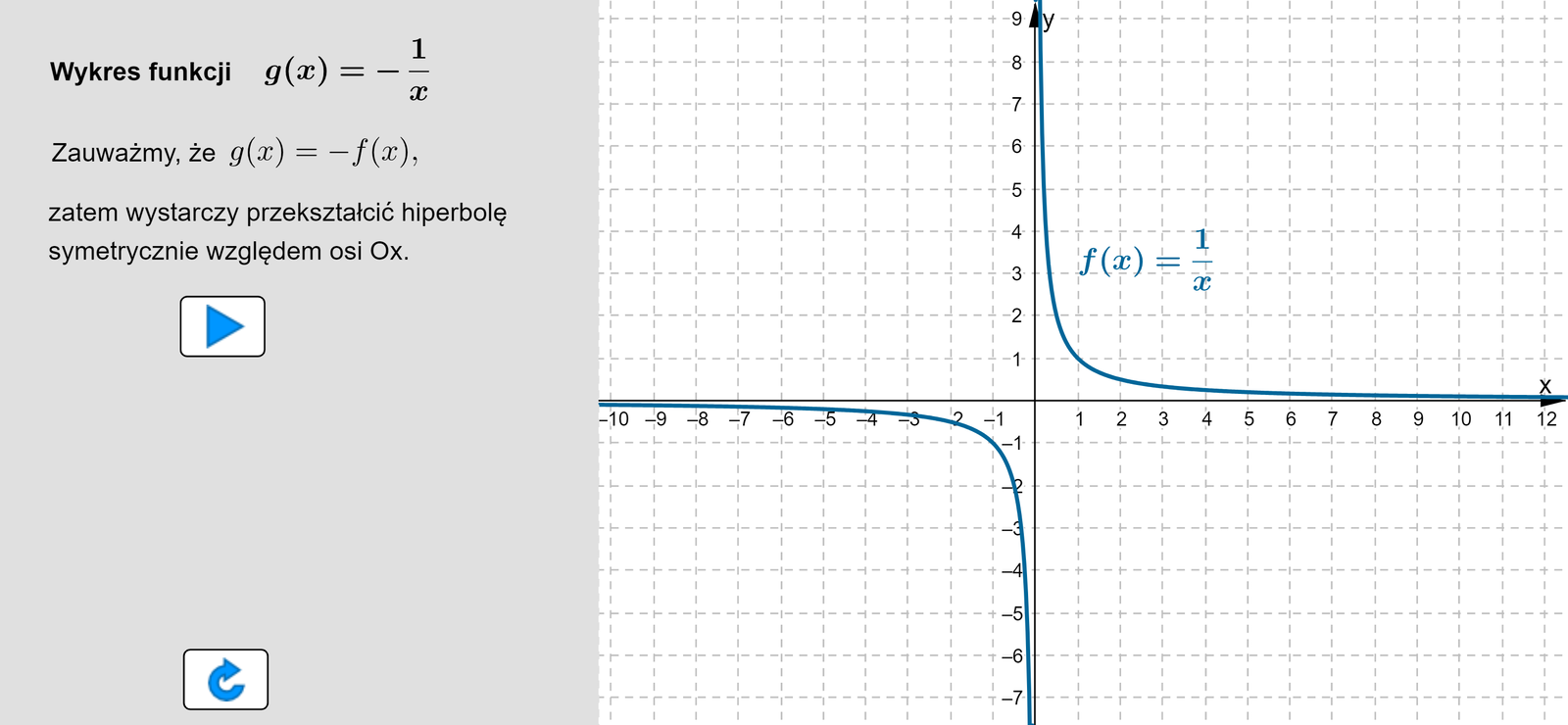
Korzystając z wykresu funkcji , narysuj wykres funkcji .
Zapoznaj się z opisem poniższego apletu.
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/Pbfh3SsUp
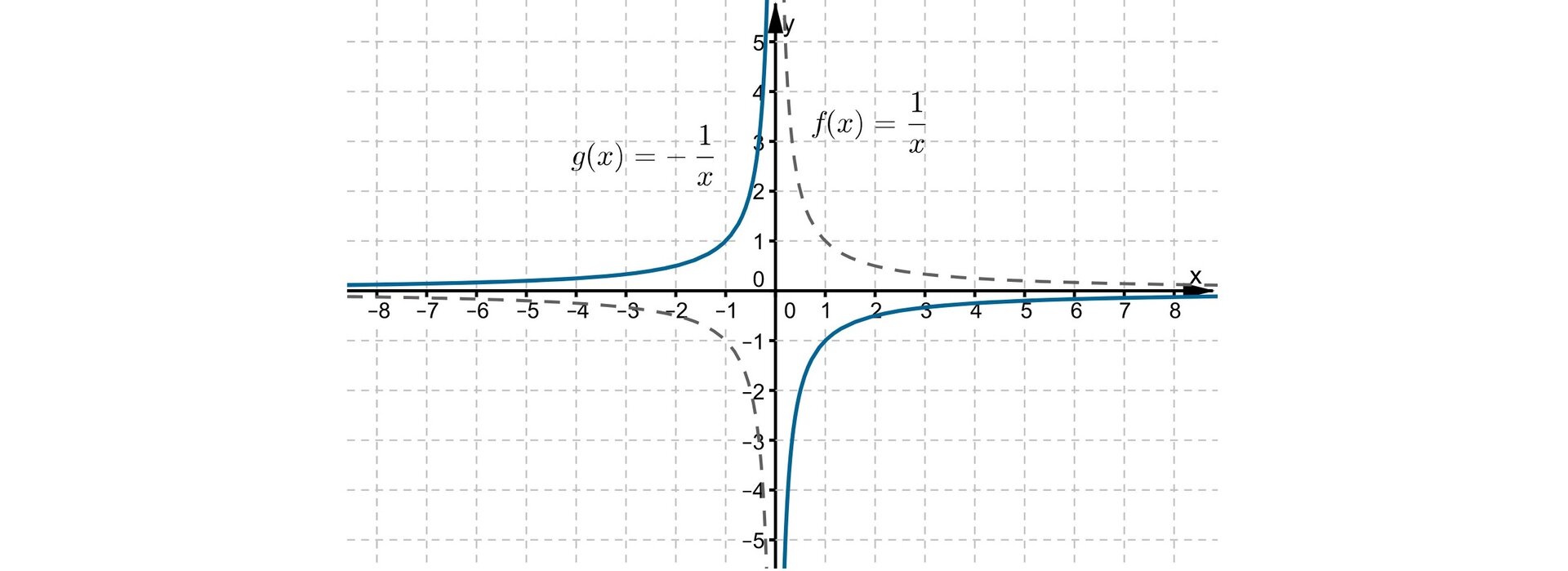
Odczytamy z wykresu własności funkcji .
Ramiona hiperboli leżą w i ćwiartce układu współrzędnych.
Funkcja jest określona dla wszystkich (wykres funkcji nie przecina osi ).
Zbiorem wartości jest przedział .
Funkcja nie ma miejsc zerowych (wykres funkcji nie ma punktów wspólnych z osią ).
Funkcja jest rosnąca w każdym z przedziałów oraz .
Funkcja przyjmuje wartości dodatnie dla argumentów z przedziału oraz wartości ujemne dla argumentów z przedziału .
Wykorzystując poniższy aplet sprawdź:
w jaki sposób wartość współczynnika wpływa na położenie wykresu,
jaki związek zachodzi pomiędzy polem prostokąta wyznaczonego przez punkt wykresu a współczynnikiem .
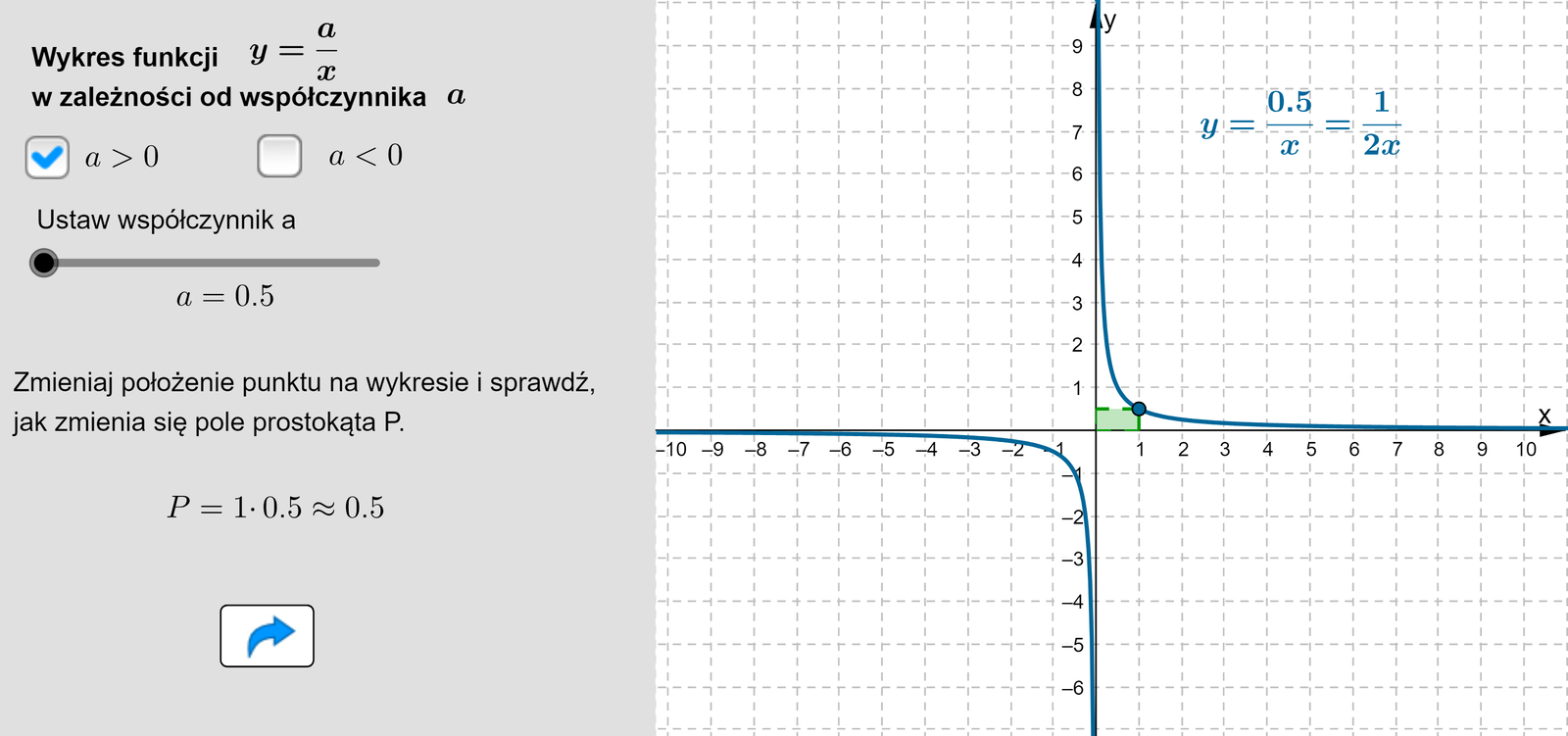
Analizując opis poniższego apletu, dowiesz się:
w jaki sposób wartość współczynnika wpływa na położenie wykresu,
jaki związek zachodzi pomiędzy polem prostokąta wyznaczonego przez punkt wykresu a współczynnikiem .
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/Pbfh3SsUp
Odpowiedź:
Dla dodatniego współczynnika hiperbola leży w pierwszej i trzeciej ćwiartce układu współrzędnych, a dla ujemnego współczynnika hiperbola leży w drugiej i czwartej ćwiartce układu współrzędnych.
Pole każdego prostokąta jest równe danej wartości współczynnika .
Narysuj wykres . Odczytaj z wykresu najmniejszą wartość funkcji w przedziale
Przeanalizuj poniższy opis funkcji i wskaż najmniejszą wartość tej funkcji w przedziale

Odpowiedź. Najmniejsza wartość funkcji w przedziale jest równa .
Punkt leży na wykresie proporcjonalności odwrotnej . Wyznacz wartość współczynnika .
Z tego, że punkt leży na wykresie , wynika, że , czyli .
Narysuj wykres funkcji . Odczytaj z wykresu, dla jakich argumentów funkcja przyjmuje wartości mniejsze od .
Przeanalizuj poniższy opis funkcji i wskaż argumenty, dla których funkcja przyjmuje wartości mniejsze od .

Odpowiedź. Funkcja przyjmuje wartości mniejsze od dla argumentów z przedziału .
Połącz w pary wzór hiperboli z punktem, który do niej należy.
<math><mo>(</mo><mn>0</mn><mo>,</mo><mn>0</mn><mo>)</mo></math>, <math><mo>(</mo><mo>-</mo><mn>1</mn><mo>,</mo><mn>1</mn><mo>)</mo></math>, <math><mo>(</mo><mn>2</mn><mo>,</mo><mn>0</mn><mo>)</mo></math>, <math><mo>(</mo><mo>-</mo><mn>3</mn><mo>,</mo><mo>-</mo><mn>1</mn><mo>)</mo></math>