Wyłączanie wspólnego czynnika przed nawias
Jeżeli w każdym ze składników sumy algebraicznej występuje taki sam czynnik, to można ten wspólny czynnik wyłączyć przed nawias.
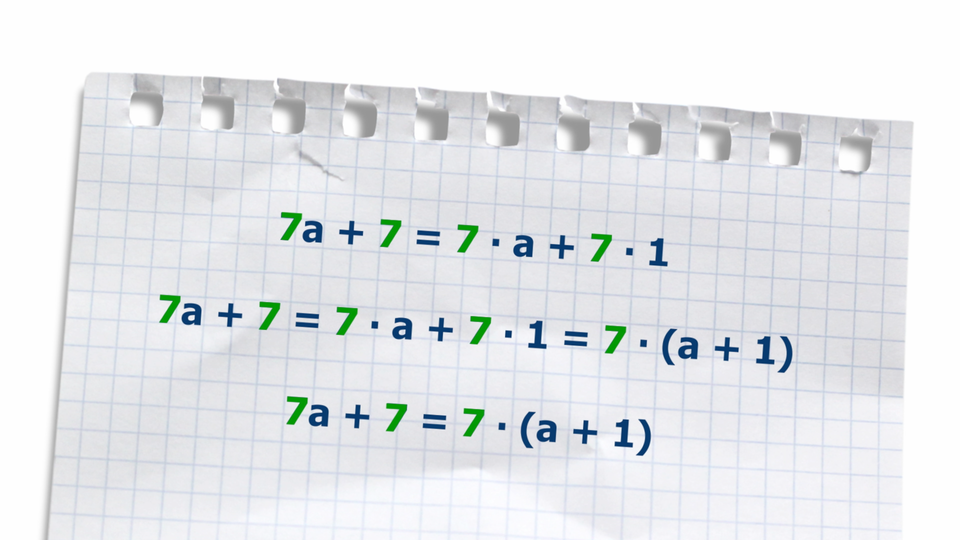
Film dostępny pod adresem /preview/resource/R4BSbCSr1g87q
Animacja przedstawia w jaki sposób możemy wyłączyć wspólny czynnik przed nawias w pewnym wyrażeniu.
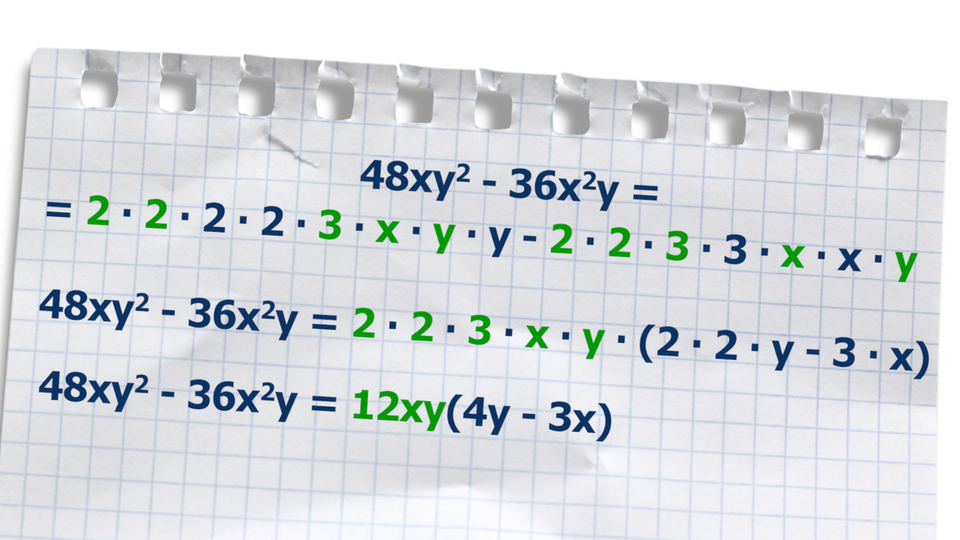
Film dostępny pod adresem /preview/resource/Ra4KEScGTCvC6
Animacja przedstawia w jaki sposób możemy wyłączyć wspólny czynnik przed nawias w pewnym wyrażeniu.
Wyłączanie wspólnego czynnika przed nawias to zamiana sumy algebraicznej na iloczyn.
Wyłącz największy wspólny czynnik przed nawias.
Wyłącz wspólny czynnik przed nawias i doprowadź wyrażenie w nawiasie do najprostszej postaci.
Przeciągnij i upuść podane wyrażenia tak, aby otrzymane równości były prawdziwe.
, , , , , , ,
a)
b)
c)
d)
e)
-
2 xy ( 10 x 2 y 3 – 7 x y 2 + 4 xy ) -
2 x 2 y 2 ( 10 x y 2 – 7 y + 4 ) -
2 x 2 ( 10 x y 4 – 7 y 3 + 4 y 2 ) -
2 y 2 ( 10 x 3 y 2 – 7 x 2 y + 4 x 2 )
-
( 3 x – 4 y ) ( - 3 xy + 8 z ) -
( 3 x – 4 y ) ( - xy – 2 z ) -
( 3 x – 4 y ) ( - 3 xy – 2 z ) -
( 3 x – 4 y ) ( - xy + 8 z )
-
Długość boku kwadratu o obwodzie
8 a 2 + 12 ab 2 a + 3 b -
Szerokość prostokąta o polu
9 x 2 y 2 + 6 xy 2 3 xy 2 3 x + 2 -
Wysokość trapezu o polu
1 2 x 2 1 4 xy x x + 1 2 y -
Długość przekątnej rombu o polu
0,25 a 2 b + 1,5 ab ab 0,5 a + 0,3
Przeciągnij i upuść podane wyrażenia tak, aby otrzymane równości były prawdziwe.
a)
b)
c)
d)
e)
Połącz w pary.
<span aria-label="dwa x indeks górny, dwa, y nawias pięć x indeks górny, dwa, y, minus, cztery x y indeks górny, dwa, plus, dwa zamknięcie nawiasu" role="math"><math><mn>2</mn><msup><mi>x</mi><mn>2</mn></msup><mi>y</mi><mo>(</mo><mn>5</mn><msup><mi>x</mi><mn>2</mn></msup><mi>y</mi><mo>-</mo><mn>4</mn><mi>x</mi><msup><mi>y</mi><mn>2</mn></msup><mo>+</mo><mn>2</mn><mo>)</mo></math></span>, <span aria-label="trzy x indeks górny, dwa, y indeks górny, dwa, nawias dwa x, minus, jeden, plus, cztery y zamknięcie nawiasu" role="math"><math><mn>3</mn><msup><mi>x</mi><mn>2</mn></msup><msup><mi>y</mi><mn>2</mn></msup><mo>(</mo><mn>2</mn><mi>x</mi><mo>-</mo><mn>1</mn><mo>+</mo><mn>4</mn><mi>y</mi><mo>)</mo></math></span>, <span aria-label="dwa x y nawias dwa y indeks górny, dwa, minus, sześć x y, plus, trzy x zamknięcie nawiasu" role="math"><math><mn>2</mn><mi>x</mi><mi>y</mi><mo>(</mo><mn>2</mn><msup><mi>y</mi><mn>2</mn></msup><mo>-</mo><mn>6</mn><mi>x</mi><mi>y</mi><mo>+</mo><mn>3</mn><mi>x</mi><mo>)</mo></math></span>, <span aria-label="dwa x y nawias x y indeks górny, dwa, minus, dwa y, plus, cztery x zamknięcie nawiasu" role="math"><math><mn>2</mn><mi>x</mi><mi>y</mi><mo>(</mo><mi>x</mi><msup><mi>y</mi><mn>2</mn></msup><mo>-</mo><mn>2</mn><mi>y</mi><mo>+</mo><mn>4</mn><mi>x</mi><mo>)</mo></math></span>, <span aria-label="sześć x indeks górny, dwa, y indeks górny, dwa, nawias trzy x y indeks górny, dwa, minus, y, plus, dwa x indeks górny, dwa, zamknięcie nawiasu" role="math"><math><mn>6</mn><msup><mi>x</mi><mn>2</mn></msup><msup><mi>y</mi><mn>2</mn></msup><mo>(</mo><mn>3</mn><mi>x</mi><msup><mi>y</mi><mn>2</mn></msup><mo>-</mo><mi>y</mi><mo>+</mo><mn>2</mn><msup><mi>x</mi><mn>2</mn></msup><mo>)</mo></math></span>
Ania kupiła
Podstawą prostopadłościanu jest prostokąt o bokach
Wykaż, że suma trzech kolejnych liczb nieparzystych, z których najmniejszą jest
Wykaż, że różnica liczby trzycyfrowej, której cyfrą setek jest
Wyznacz, za pomocą wyłączania wspólnego czynnika przed nawias, długość boku kwadratu, którego obwód jest równy obwodowi prostokąta o bokach
Wykaż, że suma kwadratów trzech kolejnych liczb parzystych, z których najmniejszą jest