R1CvjCqdPtfJL

Oto przykład zagadki takiego typu, jaki był popularny w $XIX$ wieku.

RH0wB7VWYhG6Y

Ilustracja przedstawia kobietę, która mówi "Pomyślałam pewną liczbę, dodałam do niej pięć, wynik podzieliłam przez dwa i otrzymane wyrażenie pomnożyłam przez sześć. Od otrzymanego iloczynu odjęłam piętnaście, wynik podzieliłam przez trzy i otrzymałam dwa. Jaką liczbę pomyślałam?". — Źródło: dostępny w internecie: Flickr.com, licencja: CC BY 2.0.

Najłatwiej rozwiązać zagadkę, zapisując kolejne obliczenia w postaci wyrażeń algebraicznych.

W tym materiale zbierzemy wiadomości dotyczące takich wyrażeń, sposobów ich przekształcania, obliczania ich wartości liczbowych, zapisywania zależności przedstawionych w zadaniach za ich pomocą.

Interaktywna treść merytorycznaInteraktywna treść merytoryczna
Gra edukacyjnaGra edukacyjna
Test samosprawdzającyTest samosprawdzający
Zestaw ćwiczeń interaktywnychZestaw ćwiczeń interaktywnych
SłownikSłownik

Twoje cele

Zapiszesz zależności przedstawione w zadaniach w postaci wyrażeń algebraicznych jednej lub kilku zmiennych.
Przekształcisz wyrażenie algebraiczne i zapiszesz je w najprostszej postaci.
Obliczysz wartość liczbową wyrażenia algebraicznego.
Zapiszesz rozwiązanie zadania w postaci wyrażenia algebraicznego.

W wielu zagadnieniach z różnych dziedzin wiedzy, ale też i praktycznych, zamiast liczb stosujemy oznaczenia literowe. Umożliwia to rozwiązanie problemów w postaci ogólnej.

Z liter, liczb, znaków działań oraz nawiasów, tworzymy wyrażenia algebraicznewyrażenie algebraicznewyrażenia algebraiczne.

RQwpxyXJouTxc

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Przykład 1

Figury na rysunku składają się z jednakowych kwadratów. Liczbę tych kwadratów opisano za pomocą wyrażenia arytmetycznego pod każdą z figur.

R1Xt5HbiUxScd

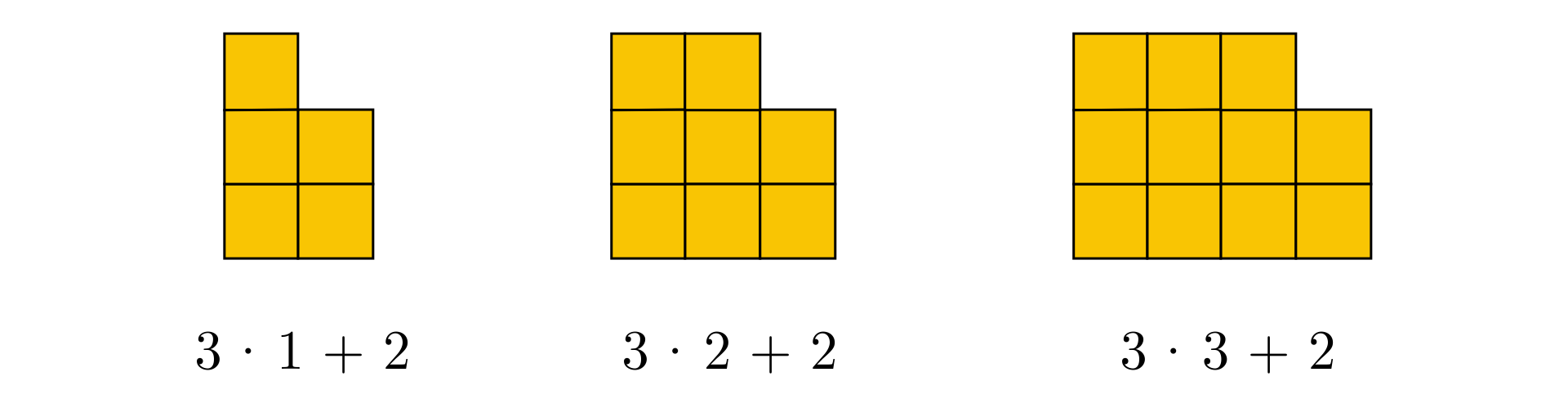
Ilustracja przedstawia trzy figury. Pierwsza od lewej składa się z dwóch pionowych rzędów. Pierwszy rząd złożony jest z trzech takich samych kwadratów, a drugi rząd jest złożony z dwóch takich samych kwadratów. Pod pierwszą figurą zapisano: trzy razy jeden dodać dwa. Druga od lewej składa się z trzech pionowych rzędów. Pierwszy rząd złożony jest z trzech takich samych kwadratów, drugi rząd jest złożony z trzech takich samych kwadratów, a trzeci rząd jest złożony z dwóch takich samych kwadratów. Pod drugą figurą zapisano: trzy razy dwa dodać dwa. Trzecia od lewej składa się z czterech pionowych rzędów. Pierwszy rząd złożony jest z trzech takich samych kwadratów, drugi rząd jest złożony z trzech takich samych kwadratów, trzeci rząd jest złożony z trzech takich samych kwadratów, a czwarty rząd jest złożony z dwóch takich samych kwadratów. Pod trzecią figurą zapisano: trzy razy trzy dodać dwa. — Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Jeśli ponumerujemy figury, zauważymy, że w każdej sumie opisującej liczbę kwadratów, jednym ze składników jest iloczyn, składający się z liczby $3$ i numeru figury, a drugim składnikiem jest liczba $2$ .

R1PRTzOUy4q3F

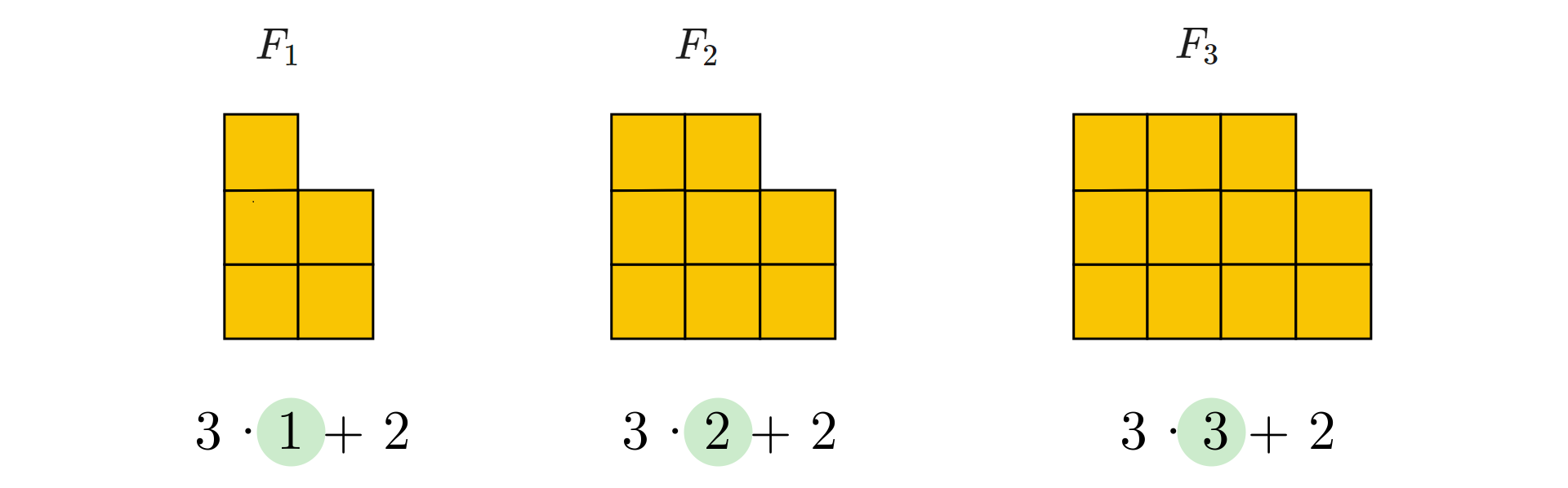
Łatwo zapisać więc za pomocą wyrażenia algebraicznego liczbę kwadratów, z których składa się $n$ –ta figura ( $n$ – liczba naturalna dodatnia).

$F_{n} = 3 \cdot n + 2$

Przykład 2

Figury na rysunku tworzone są według pewnej reguły. Odkryjemy tę regułę i ustalimy z ilu elementów zbudowana jest $n$ –ta figura $(n ⩾ 1)$ .

RkVB7SgobtnS8

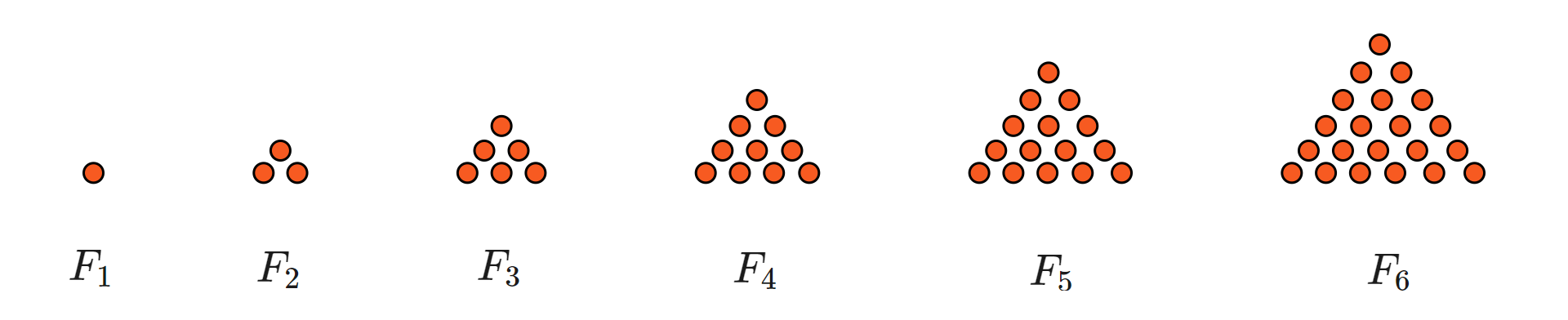
Ilustracja przedstawia sześć figur. Pierwsza z nich składa się z jednego punktu i oznaczono ją F - jeden. Kolejne figury składają się z coraz większej liczby punktów. Druga figura od lewej ma kształt trójkąta, który składa się z dwóch poziomych rzędów punktów i oznaczono ją F - dwa. W dolnym rzędzie tej figury znajdują się dwa punkty, a w górnym rzędzie znajduje się jeden punkt. Trzecia figura od lewej ma kształt trójkąta, który składa się z trzech poziomych rzędów punktów i oznaczono ją F - trzy. W dolnym rzędzie tej figury znajdują się trzy punkty, w drugim od dołu rzędzie znajdują się dwa punkty, a w górnym rzędzie znajduje się jeden punkt. Czwarta figura od lewej ma kształt trójkąta, który składa się z czterech poziomych rzędów punktów i oznaczono ją F - cztery. W dolnym rzędzie tej figury znajdują się cztery punkty, w drugim od dołu rzędzie znajdują się trzy punkty, w trzecim od dołu rzędzie znajdują się dwa punkty, w górnym rzędzie znajduje się jeden punkt. Piąta figura od lewej ma kształt trójkąta, który składa się z pięciu poziomych rzędów punktów i oznaczono ją F -pięć. W dolnym rzędzie tej figury znajduje się pięć punktów, w drugim od dołu rzędzie znajdują się cztery punkty, w trzecim od dołu rzędzie znajdują się trzy punkty, w czwartym od dołu rzędzie znajdują się dwa punkty, w górnym rzędzie znajduje się jeden punkt. Szósta figura od lewej ma kształt trójkąta, który składa się z sześciu poziomych rzędów punktów i oznaczono ją F - sześć. W dolnym rzędzie tej figury znajduje się sześć punktów, w drugim od dołu rzędzie znajduje się pięć punktów, w trzecim od dołu rzędzie znajdują się cztery punkty, w czwartym od dołu rzędzie znajdują się trzy punkty, w piątym od dołu rzędzie znajdują się dwa punkty, a w górnym rzędzie znajduje się jeden punkt. — Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Policzmy najpierw, z ilu elementów składa się każda z figur na rysunku.

RTGwsFlwJaR3W

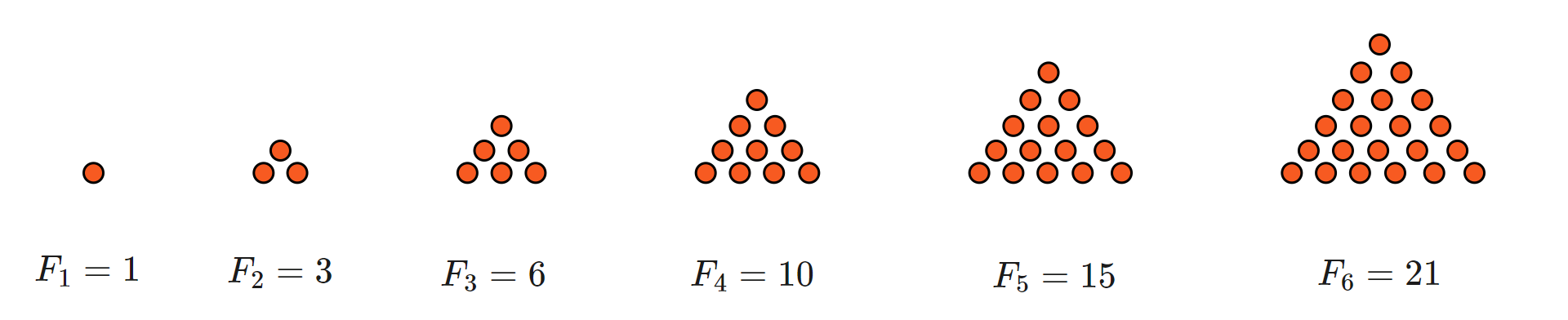
Ilustracja przedstawia sześć figur. Pierwsza z nich składa się z jednego punktu, oznaczono ją F - jeden i zapisano F - jeden równa się jeden. Kolejne figury składają się z coraz większej liczby punktów. Druga figura od lewej ma kształt trójkąta, który składa się z dwóch poziomych rzędów punktów, oznaczono ją F - dwa i zapisano F - dwa równa się trzy. W dolnym rzędzie tej figury znajdują się dwa punkty, a w górnym rzędzie znajduje się jeden punkt. Trzecia figura od lewej ma kształt trójkąta, który składa się z trzech poziomych rzędów punktów, oznaczono ją F - trzy i zapisano F - trzy równa się sześć. W dolnym rzędzie tej figury znajdują się trzy punkty, w drugim od dołu rzędzie znajdują się dwa punkty, a w górnym rzędzie znajduje się jeden punkt. Czwarta figura od lewej ma kształt trójkąta, który składa się z czterech poziomych rzędów punktów, oznaczono ją F - cztery i zapisano F - cztery równa się dziesięć. W dolnym rzędzie tej figury znajdują się cztery punkty, w drugim od dołu rzędzie znajdują się trzy punkty, w trzecim od dołu rzędzie znajdują się dwa punkty, w górnym rzędzie znajduje się jeden punkt. Piąta figura od lewej ma kształt trójkąta, który składa się z pięciu poziomych rzędów punktów, oznaczono ją F - pięć i zapisano F - pięć równa się piętnaście. W dolnym rzędzie tej figury znajduje się pięć punktów, w drugim od dołu rzędzie znajdują się cztery punkty, w trzecim od dołu rzędzie znajdują się trzy punkty, w czwartym od dołu rzędzie znajdują się dwa punkty, w górnym rzędzie znajduje się jeden punkt. Szósta figura od lewej ma kształt trójkąta, który składa się z sześciu poziomych rzędów punktów, oznaczono ją F - sześć i zapisano F - sześć równa się dwadzieścia jeden. W dolnym rzędzie tej figury znajduje się sześć punktów, w drugim od dołu rzędzie znajduje się pięć punktów, w trzecim od dołu rzędzie znajdują się cztery punkty, w czwartym od dołu rzędzie znajdują się trzy punkty, w piątym od dołu rzędzie znajdują się dwa punkty, a w górnym rzędzie znajduje się jeden punkt. — Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Chcemy znaleźć zależność między numerem figury, a liczbą elementów, z których jest zbudowana.

F_{1} = 1 = 1 \cdot \frac{2}{2}

F_{2} = 3 = 2 \cdot \frac{3}{2}

F_{3} = 6 = 3 \cdot \frac{4}{2}

F_{4} = 10 = 4 \cdot \frac{5}{2}

F_{5} = 15 = 5 \cdot \frac{6}{2}

F_{6} = 21 = 6 \cdot \frac{7}{2}

Zauważmy, że liczba elementów danej figury jest równa iloczynowi numeru tej figury i połowy numeru figury następnej.
Zatem figura o numerze $n$ składa się z $n \cdot \frac{n + 1}{2}$ elementów.

F_{n} = n \cdot \frac{n + 1}{2}

Liczbę elementów, z których składa się figura o numerze $n$ zapisaliśmy za pomocą wyrażenia algebraicznego.

Litery występujące w wyrażeniach algebraicznych to zmienne. Wstawiając w miejsce zmiennych dane liczby i wykonując wskazane działania, obliczamy wartość liczbową wyrażenia algebraicznegowyrażenie algebraicznewyrażenia algebraicznego.

Przykład 3

Pole $P$ trójkąta o bokach długości $a$ , $b$ , $c$ można obliczyć ze wzoru
${(4 P)}^{2} = 4 a^{2} b^{2} - {(a^{2} + b^{2} - c^{2})}^{2}$ .
Obliczymy, korzystając z tego wzoru, pole trójkąta o bokach długości $5$ , $5$ , $8$ .
Podstawiamy do wzoru w miejsce zmiennych, odpowiednio
$a = 5$ , $b = 5$ , $c = 8$ .

{(4 P)}^{2} = 4 a^{2} b^{2} - {(a^{2} + b^{2} - c^{2})}^{2}

{(4 P)}^{2} = 4 \cdot 5^{2} \cdot 5^{2} - {(5^{2} + 5^{2} - 8^{2})}^{2}

Wykonujemy wskazane działania.

{(4 P)}^{2} = 4 \cdot 25 \cdot 25 - {(25 + 25 - 64)}^{2}

{(4 P)}^{2} = 2500 - {(- 14)}^{2}

{(4 P)}^{2} = 2500 - 196

{(4 P)}^{2} = 2304

Obie strony wyrażenia są dodatnie, więc pierwiastkujemy obie strony zapisanego wyrażenia.

4 P = 48

P = 12

Odpowiedź:
Pole trójkąta jest równe $12$ .

Wyrażenie algebraicznewyrażenie algebraiczneWyrażenie algebraiczne, w którym występują tylko liczby i zmienne, połączone znakiem mnożenia, nazywamy jednomianem.

Przykład 4

$4 a b c^{2}$ – jednomian uporządkowany (jednomian, w którym najpierw zapisany jest współczynnik liczbowy, a następnie czynniki literowe w kolejności alfabetycznej)
$2 a^{3} x$ , $7 a^{3} x$ – jednomiany podobne (jednomiany różniące się tylko współczynnikami liczbowymi)
$4 x + y - 6$ – suma algebraiczna (suma jednomianów).

Wyrażenia algebraicznewyrażenie algebraiczneWyrażenia algebraiczne można przekształcać zgodnie z kolejnością wykonywania działań.

Postępowanie polegające na zastąpieniu sumy jednomianów podobnych jednym jednomianem, nazywamy redukcją wyrazów podobnych.

Przykład 5

Zapiszemy w najprostszej postaci wyrażenie $W = 4 x - y + 2 + 6 x - 10 x + 2 y - 2$ .

Korzystamy z przemienności dodawania i grupujemy wyrazy podobne.

W = 4 x - y + 2 + 6 x - 10 x + 2 y - 2

W = (4 x + 6 x - 10 x) + (- y + 2 y) + (2 - 2)

Redukujemy w nawiasach wyrazy podobne.

W = y

Mnożąc sumę algebraiczną przez liczbę (lub przez jednomian), korzystamy z prawa rozdzielności mnożenia względem dodawania.

Aby pomnożyć dwie sumy algebraiczne, należy każdy wyraz pierwszej sumy pomnożyć przez każdy wyraz drugiej sumy i otrzymane jednomiany dodać.

Przykład 6

Zapiszemy w najprostszej postaci sumę, różnicę i iloczyn wyrażeń $W = 2 x y - 6 x^{2}$ i $U = 2 x y + x^{2}$ .

Wyrażenie	Najprostsza postać wyrażenia
$W + U$	$(2 x y - 6 x^{2}) + (2 x y + x^{2}) = 2 x y - 6 x^{2} + 2 x y + x^{2} = 4 x y - 5 x^{2}$
$W - U$	$(2 x y - 6 x^{2}) - (2 x y + x^{2}) = 2 x y - 6 x^{2} - 2 x y - x^{2} = - 7 x^{2}$
$W \cdot U$	$(2 x y - 6 x^{2}) \cdot (2 x y + x^{2}) = 4 x^{2} y^{2} + 2 x^{3} y - 12 x^{3} y - 6 x^{4} = 4 x^{2} y^{2} - 10 x^{3} y - 6 x^{4}$

Aby obliczyć wartość liczbową wyrażenia algebraicznegowyrażenie algebraicznewyrażenia algebraicznego, do danego wyrażenia w miejsce liter wstawiamy dane liczby i wykonujemy wskazane działania.

Przykład 7

Olek z Przystani Róży do Przystani Stokrotki w dół rzeki płynął łódką $45$ minut. Droga powrotna zajęła mu półtorej godziny. Prędkość własna łódki była równa $x \frac{km}{h}$ , a prędkość prądu rzeki $y \frac{km}{h}$ . Ustalimy, jaka jest odległość między przystaniami. Obliczenia wykonamy dla $x = 12 \frac{km}{h}$ , $y = 4 \frac{km}{h}$ .

Olek w dół rzeki płynął z prądem z prędkością $(x + y) \frac{km}{h}$ , a w górę rzeki pod prąd z prędkością $(x - y) \frac{km}{h}$ .

$45$ minut to $\frac{45}{60} h = \frac{3}{4} h$

Półtorej godziny to $1, 5 h = \frac{3}{2} h$ .

Długość trasy (w $km$ ) przebytej przez Olka w dół rzeki można zapisać w postaci $\frac{3}{4} \cdot (x + y)$ .

Długość trasy w (w $km$ ) przebytej przez Olka w górę rzeki można zapisać w postaci $\frac{3}{2} \cdot (x - y)$ .

Odległość z Przystani Róży do Przystani Stokrotki jest taka sama, jak odległość z Przystani Stokrotki, do Przystani Róży.

Czyli

\frac{3}{4} \cdot (x + y) = \frac{3}{2} (x - y)

Obliczamy tę odległość, podstawiając do jednej ze stron równości za $x$ liczbę $12$ , a za $y$ liczbę $4$ .

\frac{3}{4} \cdot (12 + 4) = \frac{3}{4} \cdot 16 = 12

Odległość między przystaniami jest równa $12 km$ .

Notatki

R194arO5zSZOx

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Gra edukacyjna

R2B4VoXhxrAms

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

1POZIOM ŁATWY. Test z jednomianów i wielomianów.80Brawo! Udało Ci się zaliczyć test z jednomianów i wielomianów.Niestety, nie udało Ci się zaliczyć testu. Spróbuj jeszcze raz. Powodzenia!

Test

POZIOM ŁATWY. Test z jednomianów i wielomianów.

Liczba pytań:

Limit czasu:

min

Pozostało prób:

1/1

Twój ostatni wynik:

POZIOM TRUDNY. Test z wielomianów.80Brawo! Udało Ci się zaliczyć test z wielomianów.Niestety, nie udało Ci się zaliczyć testu. Spróbuj jeszcze raz. Powodzenia!

Test

POZIOM TRUDNY. Test z wielomianów.

Liczba pytań:

Limit czasu:

min

Pozostało prób:

1/1

Twój ostatni wynik:

Polecenie 1

RghrWnSiY9P16

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Polecenie 2

Sumę liczb $2 x$ i $2$ pomnóż przez różnicę tych liczb i podziel przez $4$ .

R1cxVGfMTTpy2

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

$\frac{(2 x + 2) (2 x - 2)}{4} = \frac{4 x^{2} - 4 x + 4 x - 4}{4} = \frac{4 x^{2} - 4}{4} = x^{2} - 1$ .

Polecenie 3

Zapisz wyrażenie $- 2 - 8 (x + 1) - 7 (4 - x)$ w najprostszej postaci.

R153hpSEmJxc9

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

$- 2 - 8 (x + 1) - 7 (4 - x) = - 2 - 8 x - 8 - 28 + 7 x = - x - 38$ .

Polecenie 4

Zapisz wyrażenie $W = (3 - 2 x) (x - 1) - (x + 2) (1 - 2 x)$ w najprostszej postaci.

R7vZYNDg3EAjD

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

$W = (3 - 2 x) (x - 1) - (x + 2) (1 - 2 x)$

$W = (3 x - 3 - 2 x^{2} + 2 x) - (x - 2 x^{2} + 2 - 4 x)$

$W = (5 x - 3 - 2 x^{2}) - (- 3 x - 2 x^{2} + 2)$

$W = 5 x - 3 - 2 x^{2} + 3 x + 2 x^{2} - 2$

$W = 8 x - 5$

Test samosprawdzający

Rozwiąż test, którego celem jest usystematyzowanie wiadomości i umiejętności na temat wyrażeń algebraicznych.

Test jest dwustopniowy. Drugą, trudniejszą część testu, możesz rozwiązać dopiero, gdy zaliczysz część łatwiejszą.

Wyrażenia algebraiczne cz.2142170Brawo! To jest poprawne rozwiązanie!Niestety, to nie jest prawidłowe rozwiązanie. Zastanów się i odpowiedz jeszcze raz.1

Test

Wyrażenia algebraiczne cz.2

Liczba pytań:

Limit czasu:

21 min

Pozostało prób:

1/1

Twój ostatni wynik:

Wyrażenia algebraiczne cz.2

Pytanie 1/14

Twój ostatni wynik -

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Wyrażenia algebraiczne cz.2142170Brawo! To jest poprawne rozwiązanie!Niestety, to nie jest prawidłowe rozwiązanie. Zastanów się i odpowiedz jeszcze raz.1

Test

Wyrażenia algebraiczne cz.2

Liczba pytań:

Limit czasu:

21 min

Pozostało prób:

1/1

Twój ostatni wynik:

Wyrażenia algebraiczne cz.2

Pytanie 1/14

Twój ostatni wynik -

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Polecenie 5

Suma dwóch liczb jest równa $17$ , a ich różnica jest równa $3$ . Oblicz różnicę kwadratów tych liczb. Wzoruj się na rozwiązaniu jednego z zadań testu.

R12GTl0LgyWtu

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

a + b = 17

a - b = 3

a + b = 17

a - b = 3

(a + b) (a - b) = a^{2} - a b + a b - b^{2} = a^{2} - b^{2}

a^{2} - b^{2} = (a + b) (a - b)

a^{2} - b^{2} = 17 \cdot 3 = 51

Różnica kwadratów rozważanych liczb jest równa $51$ .

Polecenie 6

Niech $n$ będzie liczbą naturalną dodatnią.
Znajdź resztę z dzielenia liczby $30 n + 35$ przez $3$ . Skorzystaj z rozwiązania jednego z zadań zamieszczonych w teście.

R1Fn1iG5sJxyj

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Liczba podzielna przez $3$ jest iloczynem liczby $3$ i pewnej liczby całkowitej.

$30 n + 35 = 30 n + 33 + 2 = (30 n + 33) + 2 = 3 (10 n + 11) + 2$

Szukana reszta jest równa $2$ .

Polecenie 7

Zapisz podane wyrażenie w najprostszej postaci. $W = 2 (x - 1) (x + 2) - [(4 + 8) x^{2} : 4 - 4]$ .

R1aR06QmDOAQb

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

$W = 2 (x - 1) (x + 2) - [(4 + 8) x^{2} : 4 - 4]$ , $W = 2 (x^{2} + 2 x - x - 2) - (x^{2} + 2 x^{2} - 4)$ , $W = 2 x^{2} + 2 x - 4 - x^{2} - 2 x^{2} + 4$ , $W = - x^{2} + 2 x$ .

Zestaw ćwiczeń interaktywnych

RGqifBGEti4xS

Ćwiczenie 1

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

R1FSiZ5CV6Uss

Ćwiczenie 1

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Ćwiczenie 2

Rmv1F0AtGcqPw

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

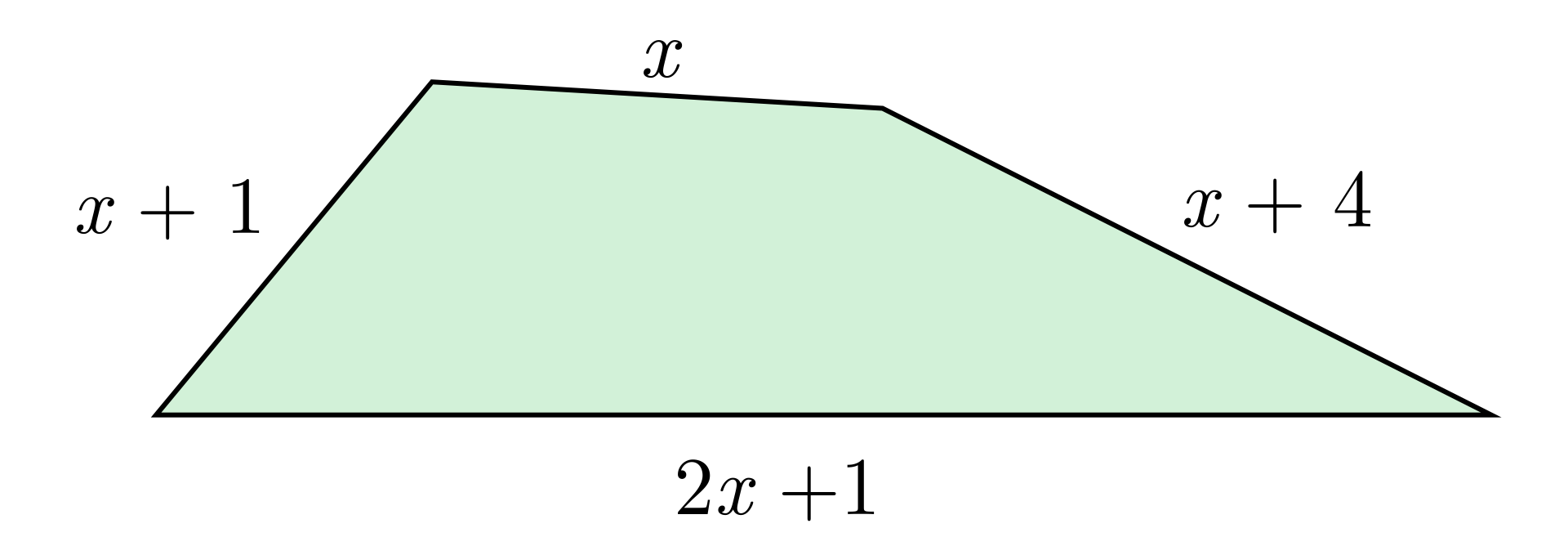
Które z podanych wyrażeń nie opisuje obwodu narysowanego czworokąta? Zaznacz prawidłową odpowiedź.

ROHxqQAUBBeOR

Ilustracja przedstawia czworokąt o bokach długości: x następnie x+1 następnie x+4 następnie 2x plus jeden. — Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

R1EBQ4ztW6JD7

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

RZxO1VeGkdWF7

Ćwiczenie 3

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

R1SfcTiuxeJv1

Ćwiczenie 4

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

R1cZIuTBvjS6M

Ćwiczenie 5

Łączenie par. Halina ma

x cm

wzrostu. Ewa jest od niej o

4 cm

wyższa. Helena jest niższa od Ewy o

6 cm

. Hanna ma

(x + 2) cm

wzrostu.
Zaznacz, które zdanie jest prawdziwe, a które fałszywe.. Najniższa z dziewcząt to Helena.. Możliwe odpowiedzi: Prawda, Fałsz. Najwyższa z dziewcząt to Hanna.. Możliwe odpowiedzi: Prawda, Fałsz. Średnia arytmetyczna wzrostu dziewcząt to

(x + 1) cm

.. Możliwe odpowiedzi: Prawda, Fałsz. Helena jest niższa od Hanny o

2 cm

.. Możliwe odpowiedzi: Prawda, Fałsz. Halina jest wyższa od Heleny o

2 cm

.. Możliwe odpowiedzi: Prawda, Fałsz

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Ruk5wEf68BWnd

Ćwiczenie 6

Połącz w pary wyrażenie i jego najprostszą postać.

2 (x - 1) + 2

Możliwe odpowiedzi: 1.

2

, 2.

- 2 x + 1

, 3.

x - 2

, 4.

2 x

, 5.

x + 3

2 x^{2} - 2 (x - 1) (x + 1)

Możliwe odpowiedzi: 1.

2

, 2.

- 2 x + 1

, 3.

x - 2

, 4.

2 x

, 5.

x + 3

4 x - x + 2 + 2 x - 4 x - 4

Możliwe odpowiedzi: 1.

2

, 2.

- 2 x + 1

, 3.

x - 2

, 4.

2 x

, 5.

x + 3

- (x - 3) + 2 x

Możliwe odpowiedzi: 1.

2

, 2.

- 2 x + 1

, 3.

x - 2

, 4.

2 x

, 5.

x + 3

(x^{2} - 2) - (x + 3) (x - 1)

Możliwe odpowiedzi: 1.

2

, 2.

- 2 x + 1

, 3.

x - 2

, 4.

2 x

, 5.

x + 3

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Ćwiczenie 7

Sumę dwóch dowolnych liczb różnych od zera pomnożono przez ich różnicę. Do wyniku dodano sumę ich kwadratów. Wykaż, że otrzymana liczba jest dodatnia.

RRlrIeHt3mAGJ

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Oznaczymy przez $a$ , $b$ dowolne liczby różne od zera. Wtedy:
$a + b$ – suma tych liczb,
$a - b$ – różnica tych liczb.

Oznaczymy przez $a$ , $b$ dowolne liczby różne od zera. Wtedy:
$a + b$ – suma tych liczb,
$a - b$ – różnica tych liczb,
$a^{2} + b^{2}$ – suma kwadratów tych liczb.

(a + b) (a - b) + (a^{2} + b^{2}) = a^{2} - a b + a b - b^{2} + a^{2} + b^{2} = 2 a^{2}

Kwadrat dowolnej liczby różnej od zera jest liczbą dodatnią. Zatem i liczba $2 a^{2}$ jest liczbą dodatnią, co należało wykazać.

Ćwiczenie 8

Kolejne figury na rysunku tworzone są z jednakowych kwadratów i sześciokątów takich, jak na rysunku. Pole takiego kwadratu jest równe $x$ , a pole sześciokąta $y$ .

R56qwPwVN2BEe

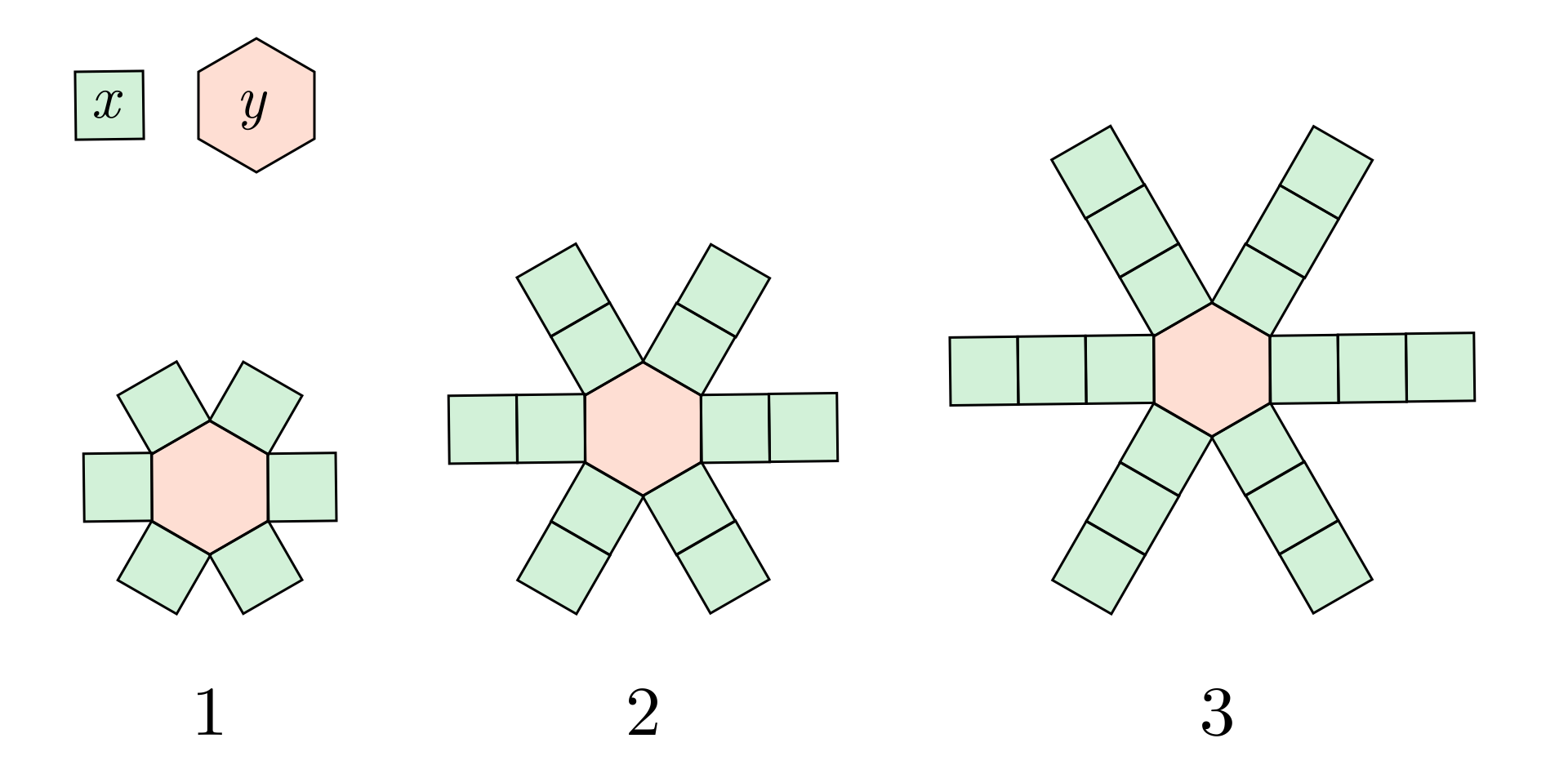
Ilustracja przedstawia kwadrat, którego pole wynosi iks, sześciokąt, którego pole wynosi igrek oraz trzy figury. Pierwsza figura składa się z sześciokąta oraz kwadratów w taki sposób, że każdy bok sześciokąta jest wspólnym bokiem z jednym kwadratem. Druga figura składa się z sześciokąta oraz kwadratów w taki sposób, że każdy bok sześciokąta jest wspólnym bokiem z figurą składającą się z dwóch kwadratów. Trzecia figura składa się z sześciokąta oraz kwadratów w taki sposób, że każdy bok sześciokąta jest wspólnym bokiem z figurą składającą się z trzech kwadratów. — Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Odkryj regułę, według której tworzone są kolejne figury. Zapisz za pomocą wyrażenia algebraicznego pole $n$ –tej takiej figury, gdzie $n$ jest liczbą naturalną dodatnią.

RHaQi09dOm9AG

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Pole pierwszej figury: $6 x + y$ .
Pole drugiej figury: $12 x + y$ .
Pole trzeciej figury: $18 x + y$ .

Pole pierwszej figury: $6 x + y = 6 \cdot 1 x + y$ .
Pole drugiej figury: $12 x + y = 6 \cdot 2 x + y$ .
Pole trzeciej figury: $18 x + y = 6 \cdot 3 x + y$ .
W każdym przypadku do kolejnej figury „dobudowujemy” sześć nowych kwadratów. Liczba określająca pole figury jest równa sumie iloczynu liczby $6$ , liczby odpowiadającej numerowi figury i liczby $x$ oraz liczby $y$ .

Zatem pole $n$ –tej figury:
$P_{n} = 6 \cdot n x + y$ .

Ćwiczenie 9

Kolejne figury na rysunku tworzone są z jednakowych zapałek według pewnej reguły tak, jak na rysunku.

R1W7VRQ0ygXoE

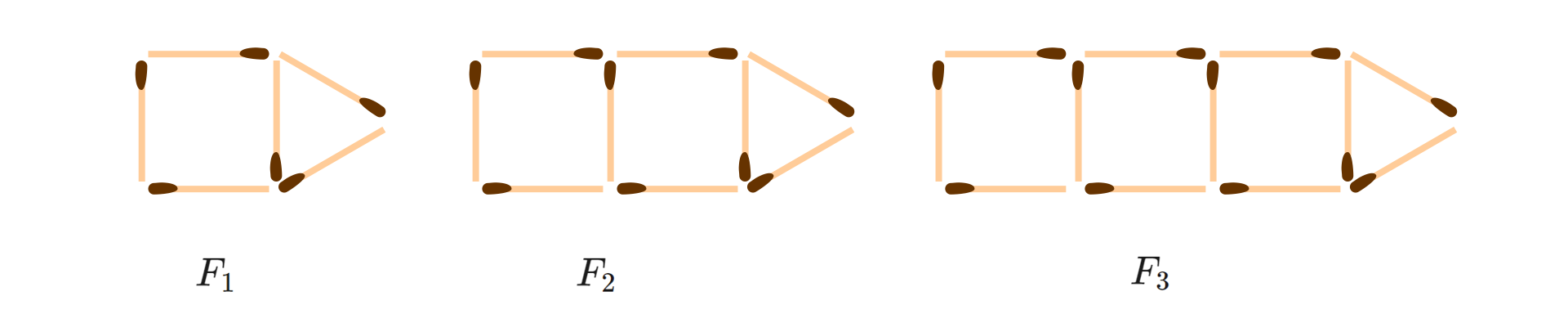
Ilustracja przedstawia trzy figury złożone z zapałek. Pierwsza figura, oznaczona ef jeden, składa się z kwadratu o boku długości jednej zapałki oraz trójkąta równobocznego o boku długości jednej zapałki i jest zbudowana tak, że mają one ze sobą jeden wspólny bok. Druga figura, oznaczona ef dwa, składa się z dwóch kwadratów o boku długości jednej zapałki oraz trójkąta równobocznego o boku długości jednej zapałki i jest zbudowana tak, że kwadraty mają ze sobą jeden wspólny bok oraz jeden z kwadratów ma jeden wspólny bok z trójkątem. Trzecia figura, oznaczona ef trzy, składa się z trzech kwadratów o boku długości jednej zapałki oraz trójkąta równobocznego o boku długości jednej zapałki i jest zbudowana tak, że pierwszy i drugi kwadrat mają ze sobą jeden wspólny bok, drugi i trzeci kwadrat mają ze sobą jeden wspólny bok oraz trzeci kwadrat ma jeden wspólny bok z trójkątem. — Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Odkryj tę regułę i zapisz wzór, według którego można obliczyć liczbę zapałek figury o dowolnym numerze. Oblicz, z ilu zapałek zbudowana jest setna taka figura.

Rhmm0mDT95yAT

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Pierwsza figura składa się z $6$ zapałek.
Druga figura składa się z $6 + 3 = 9$ zapałek.
Trzecia figura składa się z $9 + 3 = 12$ zapałek.

W każdym przypadku do kolejnej figury „dokładamy” trzy nowe zapałki.

F_{1} = 3 \cdot 1 + 3

F_{2} = 3 \cdot 2 + 3

F_{3} = 3 \cdot 3 + 3

Zatem wzór pozwalający wyznaczyć liczbę zapałek potrzebnych do zbudowania $n$ –tej figury to

F_{n} = 3 \cdot n + 3

Podstawiając w powyższym wzorze $n = 100$ , otrzymujemy liczbę zapałek potrzebnych do zbudowania setnej figury

F_{100} = 3 \cdot 100 + 3 = 303

Słownik

wyrażenie algebraiczne

wyrażenie zbudowane z liczb, liter, znaków działań, nawiasów.

Bibliografia

Smullyan R., (2004), Zagadki Szeherezady i inne zdumiewające łamigłówki dawne i współczesne, Warszawa: Książka i Wiedza.