Wyznaczanie wzoru funkcji kwadratowej na podstawie pewnych informacji o tej funkcji lub o jej wykresie
Wyznaczanie wzoru funkcji kwadratowej na podstawie pewnych informacji o tej funkcji lub o jej wykresie
Przypomnijmy, że każdą funkcję kwadratową określoną wzorem
gdzie , oraz to liczby rzeczywiste, przy czym liczba jest różna od zera, możemy zapisać w postaci kanonicznej
gdzie i .
Ponadto każdą taką funkcję kwadratową, której wyróżnik jest nieujemny, możemy też zapisać w postaci iloczynowej
gdzie i to miejsca zerowe tej funkcji.
W poniższych przykładach pokażemy, w jaki sposób można wyznaczyć wzór funkcji kwadratowej na podstawie pewnych informacji o tej funkcji lub o jej wykresie.
Funkcja kwadratowa osiąga wartość najmniejszą równą .
Wyznaczymy wartość współczynnika .
Rozwiązanie.
Z treści zadania wynika, że współrzędna wierzchołka wykresu funkcji jest równa . Możemy z tego skorzystać w jeden z następujących sposobów.
sposób
Obliczamy wyróżnik funkcji
Podstawiamy do wzoru .
Stąd , , .
sposób
Ze wzoru odczytujemy pierwszą współrzędną wierzchołka wykresu funkcji . Wobec tego
stąd .
sposób
Ze wzoru odczytujemy pierwszą współrzędną wierzchołka: i . Wobec tego funkcję można zapisać wzorem w postaci kanonicznej , stąd
czyli .
sposób
Przekształcamy wzór funkcji do postaci kanonicznej
Zatem funkcja osiąga wartość najmniejszą dla . Ponieważ , to , czyli .


Film dostępny pod adresem /preview/resource/RsM5NXUfk4Zmv
Animacja przedstawia sposób wyznaczenia współczynnika c pewnej funkcji kwadratowej.
Jednym z miejsc zerowych funkcji kwadratowej jest .
Wyznaczymy wartość współczynnika .
Rozwiązanie.
sposób
Z treści zadania wynika, że
Zatem , stąd , czyli .
sposób
Z treści zadania wynika, że funkcję można zapisać w postaci iloczynowej
gdzie to drugie miejsce zerowe funkcji .
Postać iloczynową przekształcamy do postaci ogólnej, stąd
Porównując współczynniki, stwierdzamy, że oraz .
Zatem drugim pierwiastkiem jest , więc .
sposób
Z treści zadania wynika, że funkcję można zapisać w postaci iloczynowej
gdzie to drugie miejsce zerowe funkcji .
Jedynym wyrazem niezależnym od w tym wzorze jest , zatem , a stąd . Liczba jest więc miejscem zerowym funkcji , zatem
Wobec tego , , , czyli .
Wyznaczymy współrzędne wierzchołka paraboli, która jest wykresem funkcji kwadratowej
Rozwiązanie
sposób
Przekształcamy wzór funkcji do postaci ogólnej
Wobec tego współrzędne wierzchołka tej paraboli to: , . Zatem wierzchołkiem tej paraboli jest punkt .
sposób
Ponieważ wtedy i tylko wtedy, gdy lub , to funkcja ma dwa miejsca zerowe oraz . Oś symetrii paraboli, która jest wykresem funkcji to jednocześnie symetralna odcinka, którego końcami są punkty i .
Korzystając ze wzoru na współrzędne środka odcinka, stwierdzamy, że ta symetralna przechodzi przez punkt o współrzędnych , więc jest to prosta o równaniu . Stąd oraz .
Wierzchołkiem tej paraboli jest punkt .
Współrzędne wierzchołka paraboli
Obliczymy współrzędne wierzchołka paraboli, wykorzystując jej postać iloczynową . Miejsca zerowe funkcji to oraz . Osią symetrii funkcji kwadratowej jest prosta . Wierzchołek paraboli będzie więc miał współrzędne , gdzie jest wartością funkcji dla argumentu .
.
Zatem wierzchołkiem wykresu funkcji kwadratowej jest .
Obliczymy teraz współrzędne wierzchołka paraboli, wykorzystując jej postać iloczynową . Miejsca zerowe funkcji to oraz . Osią symetrii funkcji kwadratowej jest prosta . Wierzchołek paraboli będzie więc miał współrzędne , gdzie jest wartością funkcji dla argumentu .
.
Zatem wierzchołkiem wykresu funkcji kwadratowej jest .
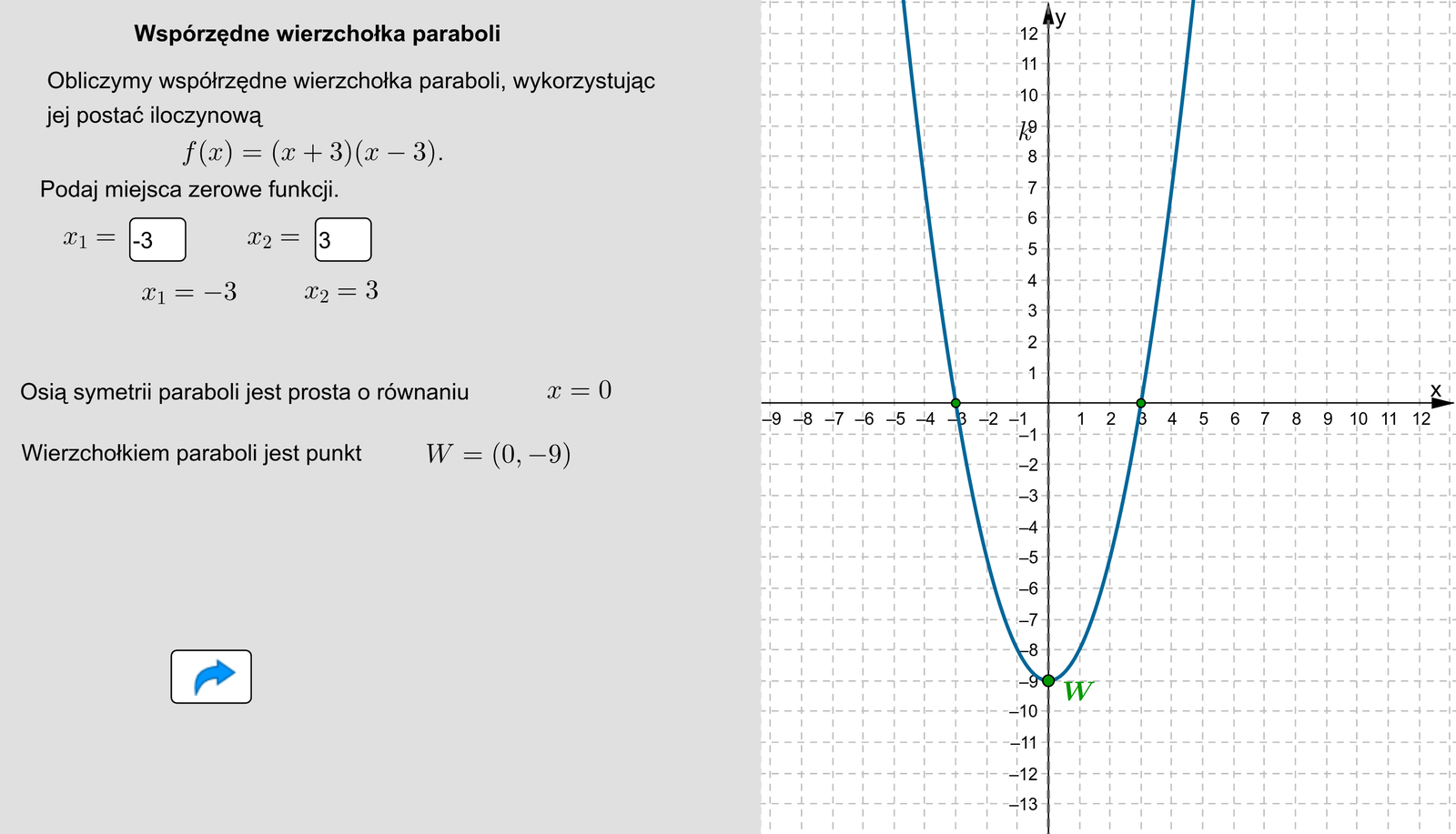
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/P7PZV0sNX
Jeżeli funkcja kwadratowa
ma dwa miejsca zerowe i , to oś symetrii paraboli będącej wykresem funkcji ma równanie
Dowód.
Jak zauważyliśmy, oś symetrii paraboli, która jest wykresem funkcji , to jednocześnie symetralna odcinka o końcach w punktach i .
Korzystając ze wzoru na współrzędne środka odcinka, stwierdzamy, że ta symetralna przechodzi przez punkt o współrzędnych . Dla dowodu wystarczy więc pokazać, że
Ponieważ
więc
Zmiana postaci ogólnej na kanoniczną.
Funkcja kwadratowa opisana jest wzorem . Postać kanoniczna tej funkcji to . Stąd otrzymujemy, że wykresem funkcji jest parabola z ramionami skierowanymi do dołu o wierzchołku w punkcie .
Funkcja kwadratowa opisana jest wzorem . Postać kanoniczna tej funkcji to . Stąd otrzymujemy, że wykresem funkcji jest parabola z ramionami skierowanymi do dołu o wierzchołku w punkcie .
Funkcja kwadratowa opisana jest wzorem . Postać kanoniczna tej funkcji to . Stąd otrzymujemy, że wykresem funkcji jest parabola z ramionami skierowanymi ku górze o wierzchołku w punkcie .
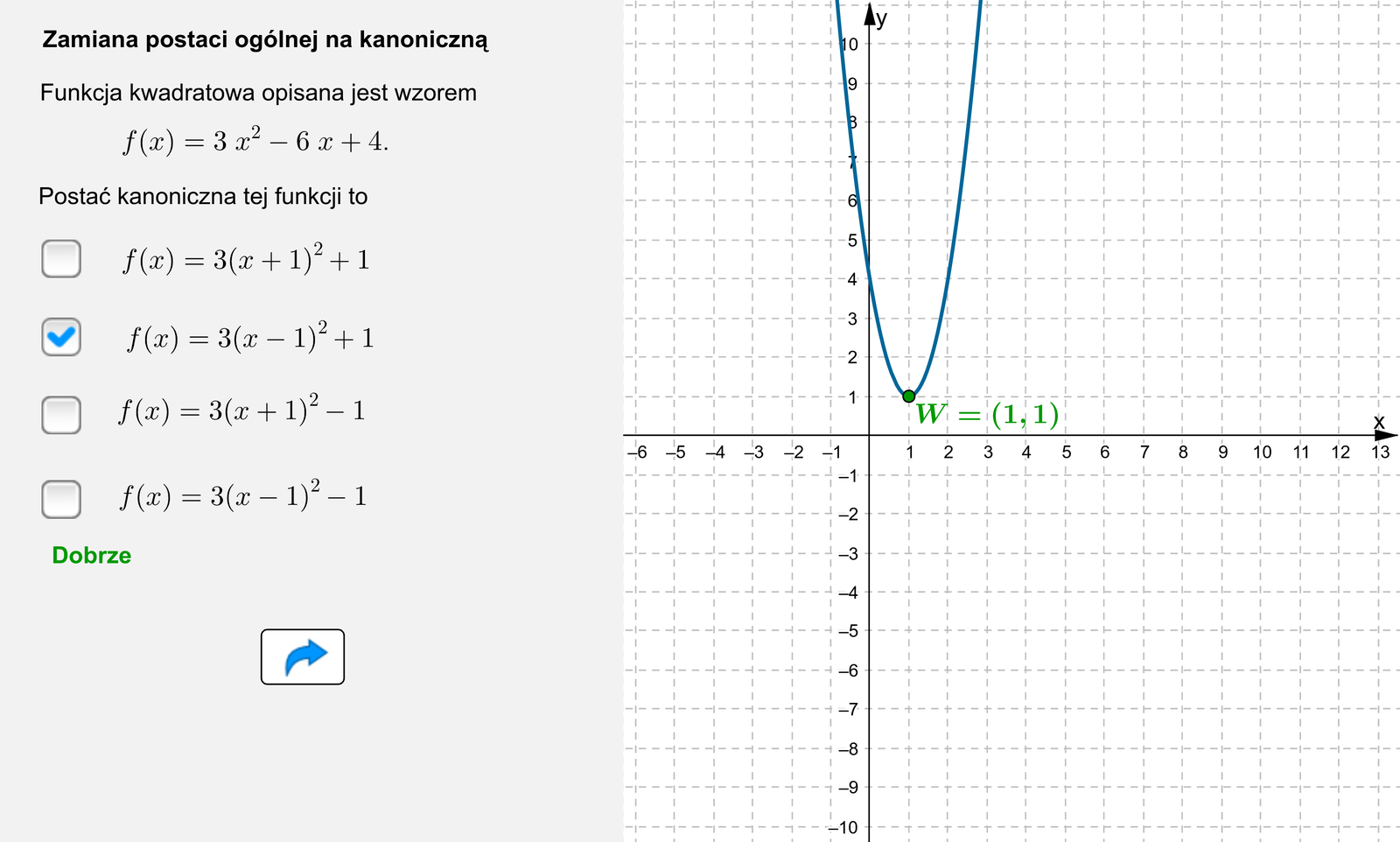
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/P7PZV0sNX
Wykresem funkcji kwadratowej określonej wzorem jest parabola o wierzchołku . Wyznaczymy wartość współczynnika i współczynnika .
Rozwiązanie.
sposób
Z treści zadania wynika, że funkcję można zapisać w postaci kanonicznej . Zatem
czyli współczynniki mają wartości , .
sposób
Korzystając ze wzorów na współrzędne wierzchołka, otrzymujemy układ równań
Uwzględniając w drugim równaniu oraz wstawiając , otrzymujemy
stąd
Mamy zatem
Funkcja kwadratowa ma dwa miejsca zerowe: i . Wyznaczymy wartość współczynnika i współczynnika .
Rozwiązanie.
sposób
Z treści zadania wynika, że funkcję można zapisać w postaci iloczynowej.
Zatem
Współczynniki mają wartości: , .
sposób
Ponieważ miejscami zerowymi funkcji są i , więc oraz . Aby wyznaczyć wartości współczynników, rozwiązujemy układ równań.
Otrzymany układ równań możemy rozwiązać dowolną metodą, np. podstawiania lub przeciwnych współczynników.
Wybierzmy metodę podstawiania
Rozwiązanie układu
metodą przeciwnych współczynników (lub każdą inną, prowadzącą do wyznaczenia wartości każdego ze współczynników) pozostawiamy jako osobne ćwiczenie.
sposób
Ponieważ miejscami zerowymi funkcji są oraz , więc osią symetrii wykresu funkcji jest prosta , czyli . Możemy więc zapisać postać kanoniczną funkcji
Wykorzystując jeszcze raz informację o miejscach zerowych, otrzymamy, że np. , stąd
czyli
Wobec tego
.
Zatem współczynniki mają wartości , .
Uwaga. Zapisując wzór funkcji w postaci i wykorzystując informację o drugim miejscu zerowym funkcji , doprowadzimy do tej samej zależności, co otrzymana powyżej . Fakt ten wynika stąd, że prosta jest symetralną odcinka o końcach w punktach i .
Funkcja kwadratowa osiąga największą wartość równą dla , a na jej wykresie leży punkt . Obliczymy wartości współczynników , i .
Rozwiązanie.
sposób
Z treści zadania wynika, że punkt jest wierzchołkiem paraboli będącej wykresem funkcji . Wobec tego wzór funkcji możemy zapisać w postaci . Wiemy ponadto, że punkt leży na wykresie funkcji , zatem . Łącząc oba uzyskane wnioski, otrzymujemy
stąd , czyli . Stąd wynika wzór funkcji
Współczynniki mają zatem wartości: , , .
sposób
Z treści zadania wynika, że jednym z miejsc zerowych funkcji jest , a osią symetrii paraboli będącej wykresem funkcji jest prosta o równaniu .
Wynika stąd, że jest drugim miejscem zerowym funkcji . Zatem wzór funkcji możemy zapisać w postaci . Wiemy ponadto, że punkt leży na wykresie funkcji , więc . Łącząc oba uzyskane wnioski, otrzymujemy
stąd , czyli . Wobec tego wzór funkcji to
Współczynniki mają więc wartości:, , .
sposób
Z treści zadania odczytujemy, że punkt oraz punkt jest wierzchołkiem paraboli będącej wykresem funkcji . Korzystając ze wzorów na współrzędne wierzchołka, otrzymujemy układ równań
Przekształcamy ten układ, uwzględniając w drugim równaniu
Stąd wniosek, że , więc , czyli , stąd . Ponieważ funkcja jest kwadratowa, więc . Zatem , stąd . Oznacza to, że , ,.
Uzupełnij lukę, wpisując odpowiednią liczbę. Wartość współczynnika wynosi Tu uzupełnij.
Zaznacz poprawną odpowiedź. Możliwe odpowiedzi: 1. , 2. , 3. , 4. , 5. , 6.
Wpisz w luki odpowiednie wartości. Wartości współczynników wynoszą Tu uzupełnij oraz Tu uzupełnij.
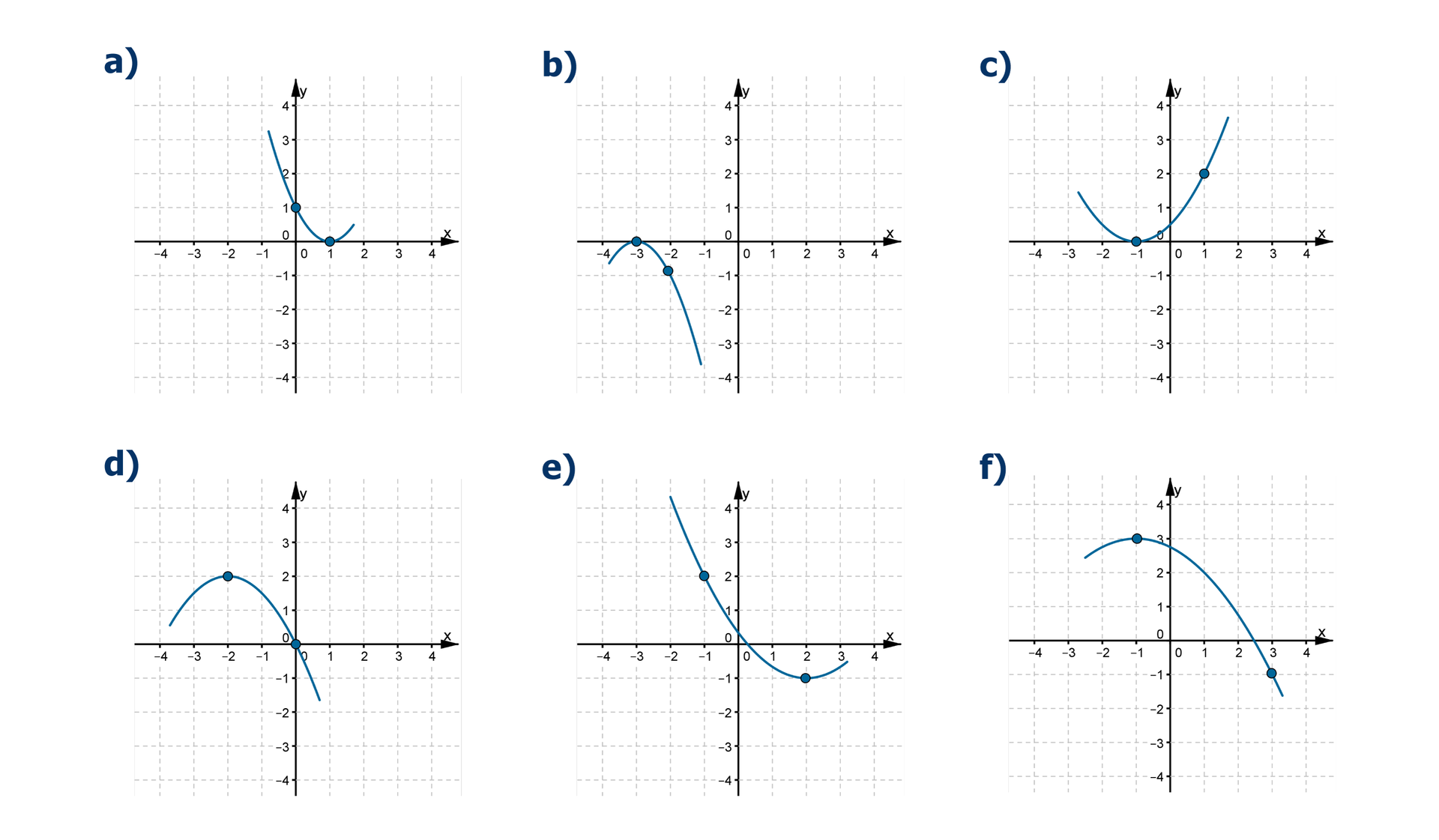
W układzie współrzędnych narysowano część paraboli, która jest wykresem funkcji kwadratowej . Wyznacz wartość każdego ze współczynników , i . Następnie połącz w pary ilustracje z odpowiednimi wartościami współczynników.
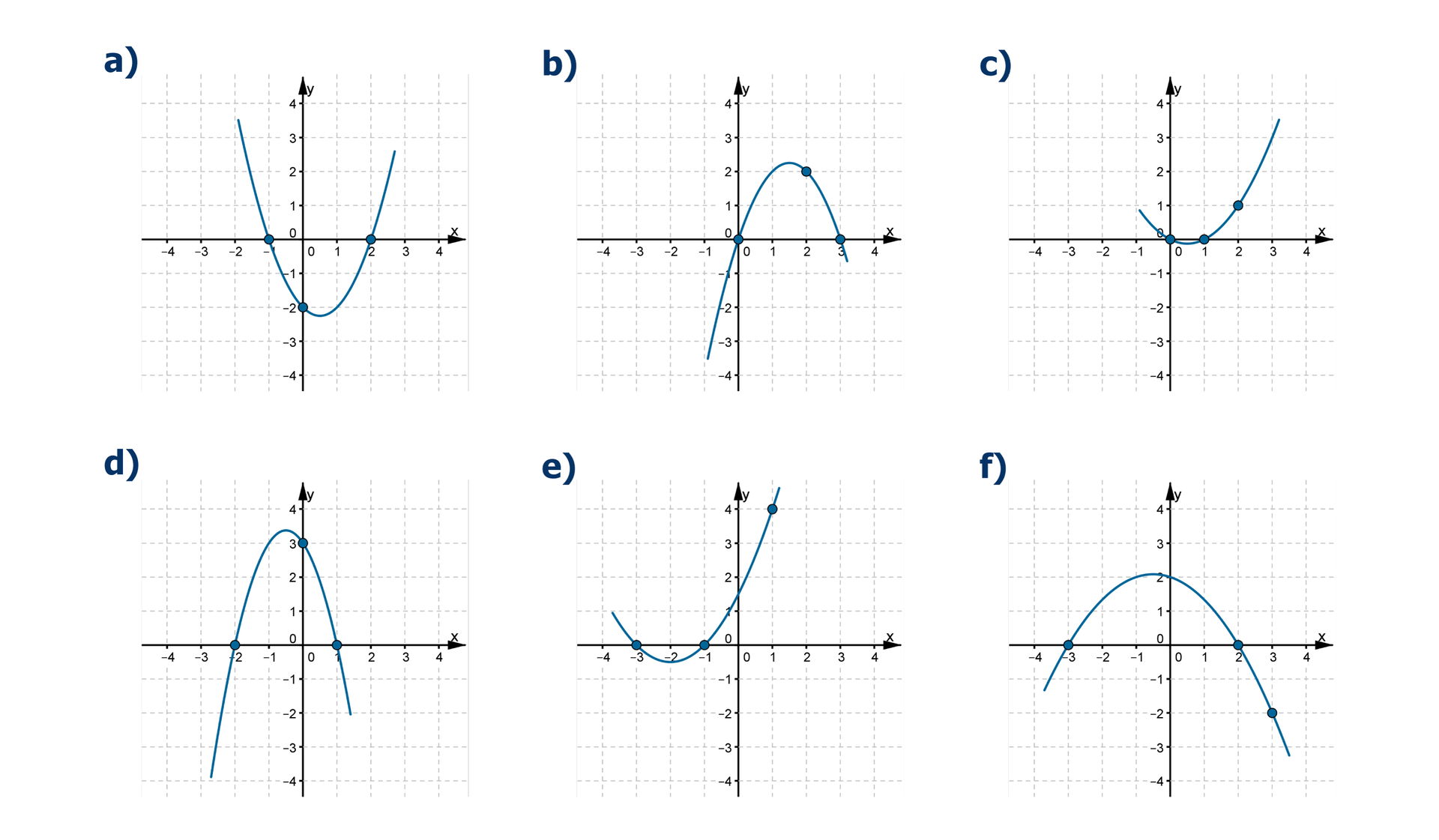
W układzie współrzędnych narysowano część paraboli, która jest wykresem funkcji kwadratowej . Ustal wartość każdego ze współczynników , i . Następnie połącz w pary ilustracje ze współczynnikami.
Punkty i leżą na paraboli, która jest wykresem funkcji kwadratowej . Wykaż, że punkt nie leży na tej paraboli.