Wzajemne położenie prostej i okręgu

Materiał ten poświęcony jest prostym oraz okręgom. Analizując zawarte tu przykłady, poznasz wzajemne położenie prostej i okręgu oraz wzajemne położenie dwóch okręgów.

Rozważmy prostą oraz okrąg o środku w punkcie $S$ i promieniu $r$ . Prosta oraz okrąg, leżące w tej samej płaszczyźnie, mogą mieć jeden punkt wspólny, mogą mieć dwa punkty wspólne lub nie mają punktów wspólnych.

RsNfisf6vssQQ11

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Wzajemne położenie prostej i okręgu
Nazwa prostej	Liczba punktów wspólnych prostej i okręgu	Interpretacja graficzna
Sieczna okręgu	dwa	R1YRY9fc4yHkG1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0. $A$ , $B$ – punkty wspólne prostej i okręgu
Styczna do okręgu	jeden	R1Dknwauqn2aj1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0. $A$ – punkt wspólny prostej i okręgu
Rozłączna z okręgiem	zero	R10HPsy98M6Um1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0. Prosta i okrąg nie mają punktów wspólnych.

Styczna do okręgu

Twierdzenie: Styczna do okręgu

Styczna do okręgu jest prostopadła do promienia tego okręgu poprowadzonego z punktu styczności.

RURN7OZ7ZQWZA1

Rysunek okręgu o środku S i promieniu r i stycznej do okręgu w punkcie C. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

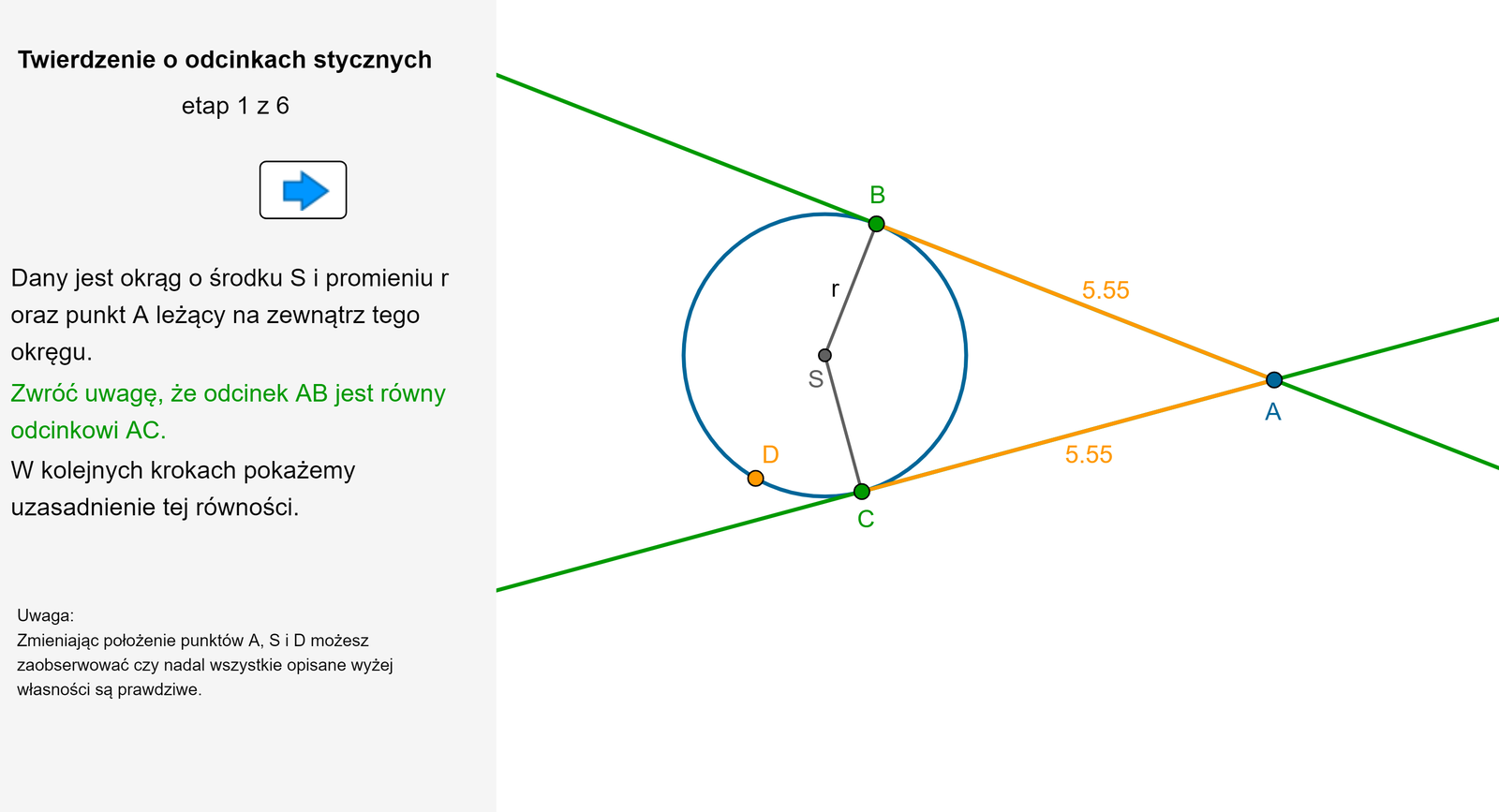
Rozważmy okrąg o środku w punkcie $S$ i promieniu $r$ oraz punkt $A$ leżący na zewnątrz tego okręgu. Poprowadźmy dwie styczne do tego okręgu przechodzące przez punkt $A$ . Punkty styczności oznaczmy $B$ i $C$ .

R19HEK663UxOk1

Rysunek dwóch stycznych AB i AC do okręgu o środku S przecinających się w punkcie A. Promień okręgu wraz z styczną tworzą kąt prosty. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Poprowadźmy odcinek $A S$ . Trójkąty $A B S$ i $A C S$ są prostokątne i mają wspólną przeciwprostokątną $S A$ . Przyprostokątne $S B$ i $S C$ mają taką samą długość $r$ . Obliczając z twierdzenia Pitagorasa trzeci z boków w obu trójkątach, otrzymujemy

|A B| = \sqrt{{|A S|}^{2} - r^{2}}

oraz

|A C| = \sqrt{{|A S|}^{2} - r^{2}}

zatem

|A B| = |A C|

R1LllDVGlJR3v11

o odcinkach stycznych

Twierdzenie: o odcinkach stycznych

Jeżeli styczne do okręgu odpowiednio w punktach $A$ i $B$ przecinają się w punkcie $C$ , to odcinki $A C$ i $B C$ są równej długości.

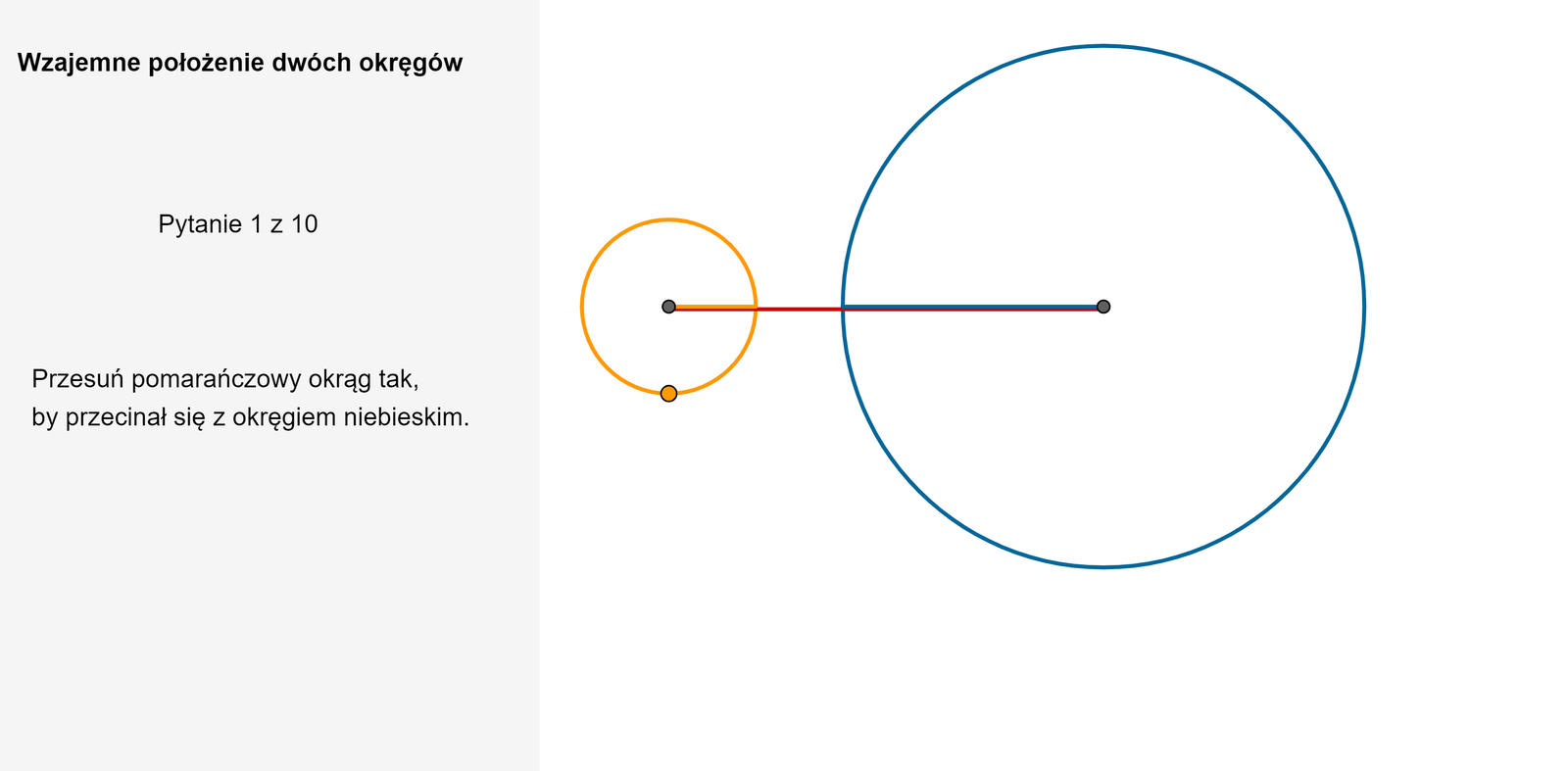
Rozważmy dwa okręgi: jeden o środku w punkcie $S_{1}$ i promieniu $r_{1}$ , drugi o środku w punkcie $S_{2}$ i promieniu $r_{2}$ , przy czym $S_{1} \neq S_{2}$ . Dwa okręgi mogą mieć dwa punkty wspólne, jeden punkt wspólny lub nie mają punktów wspólnych.

RowHt5CdzdRye11

Wzajemne położenie dwóch okręgów o różnych promieniach
Nazwa okręgów	Liczba punktów wspólnych	Zależność między środkami $S_{1}$ , $S_{2}$ okręgów a ich promieniami $r_{1}$ , $r_{2}$	Interpretacja graficzna
Okręgi przecinające się	dwa	$\|r_{1} - r_{2}\| < \|S_{1} S_{2}\|$ $< r_{1} + r_{2}$	R99Kd1LoSA7cB1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Okręgi styczne zewnętrznie	jeden	$\|S_{1} S_{2}\| = r_{1} + r_{2}$	RoUf6ii3J8pAU1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Okręgi styczne wewnętrznie	jeden	$0 < \|S_{1} S_{2}\| = \|r_{1} - r_{2}\|$	REdcxtXxoswDo1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Okręgi rozłączne zewnętrznie	zero	$\|S_{1} S_{2}\| > r_{1} + r_{2}$	R1X2DjZHerN7Z1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Okręgi rozłączne wewnętrznie	zero	$\|S_{1} S_{2}\| < \|r_{1} - r_{2}\|$	R1AVWnKamuBoh1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.