Z jaką prędkością wracać od babci, czyli wyrażenia wymierne w praktyce
Wstęp
Niekiedy zdarza się, że po przeanalizowaniu danych uzyskanych w efekcie przeprowadzonego doświadczenia, otrzymujemy zaskakujące wyniki. I to zdawałoby się sprzeczne ze zdrowym rozsądkiem.
Przykładem takiego dysonansu poznawczego jest odkrycie, że średnia prędkośćprędkość poruszających się pojazdów na drodze „tam” i „z powrotem” nie jest średnią arytmetyczną prędkości na poszczególnych odcinkach drogi.
Warto wtedy skorzystać z prostych narzędzi statystycznych, pozwalających na sprawdzenie poprawności poczynionych obserwacji.

sformułujesz i uzasadnisz wnioski na podstawie wykonywanych doświadczeń;
opiszesz prowadzone rozumowania językiem matematyki;
wykorzystasz narzędzia prawdopodobieństwa do wyboru najlepszego rozwiązania w sytuacjach z życia codziennego.
Cele edukacyjne zgodne z etapem kształcenia
Po zapoznaniu się z e‑materiałem uczeń:
dobiera i tworzy modele matematyczne przy rozwiązywaniu problemów praktycznych i teoretycznych.
Z JAKĄ PRĘDKOŚCIĄ WRACAĆ OD BABCI, CZYLI WYRAŻENIA WYMIERNE W PRAKTYCE – audiobook
Rozdziały:
Uliczna ankieta
Średnia harmoniczna
Podsumowanie
Przed rozpoczęciem pracy z audiobookiem, możesz skorzystać z przygotowanego scenariusza lekcji, który pokazuje, jak włączyć materiały multimedialne w tok lekcji.
Słuchając audiobooka, zwróćcie uwagę na sytuacje, w których intuicyjnie chcemy zastosować średnią arytmetyczną, co w konsekwencji może doprowadzić nas do uzyskania wyniku znacznie odbiegającego od poprawnego.
Przed wysłuchaniem nagrania porozmawiajcie o znanych wam, wykorzystywanych w statystyce, miarach położenia i ich zastosowaniach. Przypomnijcie sobie również, jaka jest zależność między drogą, prędkością, a czasem w ruchu jednostajnym.
Rozdział 1
Uliczna ankieta
Marcin opowiada o wynikach sondażu, który przeprowadził.
Witam wszystkich bardzo serdecznie. Mam na imię Marcin i chciałbym przedstawić wam wyniki sondażu, który przeprowadziłem wczoraj w naszym mieście. Stu przechodniów poprosiłem o rozwiązanie następującego zadania:
W środę pojechałem rowerem do babci. W jedną stronę jechałem z prędkością 20 kilometrów na godzinę. Z powrotem było z górki, więc jechałem znacznie szybciej, z prędkością 30 kilometrów na godzinę. Z jaką średnią prędkością przebyłem całą trasę "tam" i "z powrotem"?
Dziewięćdziesiąt pięć osób obliczyło średnią arytmetyczną liczb 20 i 30, czyli dwadzieścia dodać trzydzieści równa się pięćdziesiąt, pięćdziesiąt podzielić przez dwa równa się dwadzieścia pięć, i uznało, że poruszałem się ze średnią prędkością 25 kilometrów na godzinę. Tylko pięć osób podało inny wynik. Cztery stwierdziły, że średnia prędkość to 24 kilometry na godzinę. Jedna orzekła, że wynosiła ona 0 kilometrów na godzinę i upierała się, że ma rację.
Jak myślicie, który wynik jest poprawny: 25 kilometrów na godzinę czy 24 kilometry na godzinę? A może wręcz 0 kilometrów na godzinę? Przeanalizujcie problem w grupach i zaprezentujcie innym wasze obliczenia.
Rozdział 2
Średnia harmoniczna
Rozmowa Marcina z ekspertem w zakresie statystyki i matematyki.
— Aby ostatecznie rozstrzygnąć, z jaką średnią prędkością jechałem do babci i z powrotem, poprosiłem o pomoc eksperta panią Ewę, która jest nie tylko matematykiem, ale również fizykiem. Pani Ewo, czy może nam pani wyjaśnić, skąd wzięła się niespójność w wynikach uzyskanych przez ankietowanych?
— To bardzo proste. Większość respondentów, analizując zadanie zauważyła, że długość drogi, jaką przebyłeś, jadąc do babci była równa długości drogi, jaką przebyłeś w drodze powrotnej. Osoby te przyjęły więc za pewnik, że ta wielkość nie odgrywa istotnej roli w obliczeniach i pominęły ją. Średnią prędkość obliczyły, opierając się na znanych analogiach, na przykład obliczaniu średniej ocen. Korzystały więc ze średniej arytmetycznej i otrzymały rozwiązanie: 25 kilometrów na godzinę.
— Więc ten wynik jest poprawny?
— Niestety, nie.
— Gdzie zatem tkwi błąd w rozumowaniu?
— Czy pamiętasz czym jest prędkość w ruchu jednostajnym?
— Tak. Można powiedzieć, że prędkość to zmiana odległości podzielona przez jednostkę czasu, w jakiej została dokonana.
— No właśnie. W rozważanym przez nas przypadku, długość drogi „tam” była równa długości drogi „z powrotem”, ale czas jazdy był inny. Z powrotem jechałeś dużo szybciej, więc pokonałeś trasę w krótszym czasie, niż jadąc z domu do babci.
— Rzeczywiście. Jeśli więc założę, że długość drogi z domu do babci jest równa s, to cała przebyta przeze mnie droga ma długość 2s. Wtedy czas jazdy „tam” będzie wynosił s podzielić przez 20, a czas jazdy „z powrotem” s podzielić przez 30.
— Oczywiście. Aby obliczyć średnią prędkość należy podzielić długość drogi, czyli 2 s przez czas jazdy, czyli sumę, której składniki to s przez 20 i s przez 30.
— Obliczam. Mój wynik to 24 kilometry na godzinę. Czy to już jest prawidłowa odpowiedź?
— I tak, i nie.
— Jak to?
— Fizyk bez wątpienia ustaliłby, że prędkość wynosiła zero kilometrów na godzinę.
— To zaskakujące. Czy może nam pani to dokładnie wyjaśnić?
— Na co dzień posługujemy się naprzemiennie terminami prędkość i szybkość, czyli wartość prędkości. W fizyce, jednak terminy te mają inne znaczenia. Szybkość jest wielkością skalarną, czyli liczbą. Prędkość jest natomiast wielkością wektorową. Twoje przemieszczenie w podróży "tam" i "z powrotem" było równe zeru – wyjechałeś z domu i wróciłeś do domu. Stąd wniosek, że twoja średnia prędkość też była równa zeru.
— Ale średnia szybkość była równa 24 kilometry na godzinę?
— Tak. Doskonale zrozumiałeś różnicę między średnią prędkością, a średnią szybkością. Aby obliczyć średnią szybkość, utożsamianą zwykle ze średnią prędkością, wykorzystaliśmy wzór na średnią harmoniczną dwóch wielkości. Zauważ, że średnia harmoniczna w naszym przypadku była mniejsza niż średnia arytmetyczna tych samych wielkości. Czy jest tak zawsze – przedyskutuj ten problem z kolegami z klasy.
— Bardzo dziękuję za interesującą rozmowę i rozwiązanie nurtującego mnie problemu. Przy okazji uświadomiła mi też pani, że przeprowadzając sondaż należy doprecyzować zawarte w nim pytania.
Rozdział 3
Podsumowanie
Marcin podsumowuje rezultaty ankiety i rozmowy z ekspertem.
Rozmowa z naszym ekspertem zainspirowała mnie do poszukania wiadomości na temat średniej harmonicznej. W badaniach statystycznych średnia harmoniczna jest miarą położenia rozkładu, podobnie jak średnia arytmetyczna. Stosuje się ją, gdy wartości zmiennej podane są w jednostkach względnych (na przykład w km/h).
Średnią harmoniczną liczb dodatnich a1, a2, a3,…,an obliczamy jako iloraz liczby wszystkich danych przez sumę ich odwrotności. Średnia harmoniczna n liczb jest nie większa od średniej geometrycznej i nie większa od średniej arytmetycznej tych liczb. Ze średnią harmoniczną mamy do czynienia na przykład obliczając średnią szybkość, czy dobierając oporności oporników w połączeniu równoległym. A teraz zadanie dla was. Do babci pojadę samochodem z prędkością 40 kilometrów na godzinę. Z jaką prędkością muszę wracać od babci, aby moja średnia szybkość na całej trasie była równa 48 kilometrów na godzinę?
Z jaką prędkością wracać od babci, czyli wyrażenia wymierne w praktyce
Rozdział 1
Uliczna ankieta
Marcin opowiada o wynikach sondażu, który przeprowadził.
Witam wszystkich bardzo serdecznie. Mam na imię Marcin i chciałbym przedstawić wam wyniki sondażu, który przeprowadziłem wczoraj w naszym mieście. Stu przechodniów poprosiłem o rozwiązanie następującego zadania:
W środę pojechałem rowerem do babci. W jedną stronę jechałem z prędkością 20 kilometrów na godzinę. Z powrotem było z górki, więc jechałem znacznie szybciej, z prędkością 30 kilometrów na godzinę. Z jaką średnią prędkością przebyłem całą trasę „tam” i „z powrotem”?
Dziewięćdziesiąt pięć osób obliczyło średnią arytmetyczną liczb 20 i 30, czyli dwadzieścia dodać trzydzieści równa się pięćdziesiąt, pięćdziesiąt podzielić przez dwa równa się dwadzieścia pięć, i uznało, że poruszałem się ze średnią prędkością 25 kilometrów na godzinę. Tylko pięć osób podało inny wynik. Cztery stwierdziły, że średnia prędkość to 24 kilometry na godzinę. Jedna orzekła, że wynosiła ona 0 kilometrów na godzinę i upierała się, że ma rację.
Jak myślicie, który wynik jest poprawny: 25 kilometrów na godzinę czy 24 kilometry na godzinę? A może wręcz 0 kilometrów na godzinę? Przeanalizujcie problem w grupach i zaprezentujcie innym wasze obliczenia.
Rozdział 2
Średnia harmoniczna
Rozmowa Marcina z ekspertem w zakresie statystyki i matematyki.
— Aby ostatecznie rozstrzygnąć, z jaką średnią prędkością jechałem do babci i z powrotem, poprosiłem o pomoc eksperta panią Ewę, która jest nie tylko matematykiem, ale również fizykiem. Pani Ewo, czy może nam pani wyjaśnić, skąd wzięła się niespójność w wynikach uzyskanych przez ankietowanych?
— To bardzo proste. Większość respondentów, analizując zadanie zauważyła, że długość drogi, jaką przebyłeś, jadąc do babci była równa długości drogi, jaką przebyłeś w drodze powrotnej. Osoby te przyjęły więc za pewnik, że ta wielkość nie odgrywa istotnej roli w obliczeniach i pominęły ją. Średnią prędkość obliczyły, opierając się na znanych analogiach, na przykład obliczaniu średniej ocen. Korzystały więc ze średniej arytmetycznej i otrzymały rozwiązanie: 25 kilometrów na godzinę.
— Więc ten wynik jest poprawny?
— Niestety, nie.
— Gdzie zatem tkwi błąd w rozumowaniu?
— Czy pamiętasz czym jest prędkość w ruchu jednostajnym?
— Tak. Można powiedzieć, że prędkość to zmiana odległości podzielona przez jednostkę czasu, w jakiej została dokonana.
— No właśnie. W rozważanym przez nas przypadku, długość drogi „tam” była równa długości drogi „z powrotem”, ale czas jazdy był inny. Z powrotem jechałeś dużo szybciej, więc pokonałeś trasę w krótszym czasie, niż jadąc z domu do babci.
— Rzeczywiście. Jeśli więc założę, że długość drogi z domu do babci jest równa s, to cała przebyta przeze mnie droga ma długość 2s. Wtedy czas jazdy „tam” będzie wynosił s podzielić przez 20, a czas jazdy „z powrotem” s podzielić przez 30.
— Oczywiście. Aby obliczyć średnią prędkość należy podzielić długość drogi, czyli 2 s przez czas jazdy, czyli sumę, której składniki to s przez 20 i s przez 30.
— Obliczam. Mój wynik to 24 kilometry na godzinę. Czy to już jest prawidłowa odpowiedź?
— I tak, i nie.
— Jak to?
— Fizyk bez wątpienia ustaliłby, że prędkość wynosiła zero kilometrów na godzinę.
— To zaskakujące. Czy może nam pani to dokładnie wyjaśnić?
— Na co dzień posługujemy się naprzemiennie terminami prędkość i szybkość, czyli wartość prędkości. W fizyce, jednak terminy te mają inne znaczenia. Szybkość jest wielkością skalarną, czyli liczbą. Prędkość jest natomiast wielkością wektorową. Twoje przemieszczenie w podróży „tam” i „z powrotem” było równe zeru – wyjechałeś z domu i wróciłeś do domu. Stąd wniosek, że twoja średnia prędkość też była równa zeru.
— Ale średnia szybkość była równa 24 kilometry na godzinę?
— Tak. Doskonale zrozumiałeś różnicę między średnią prędkością, a średnią szybkością. Aby obliczyć średnią szybkość, utożsamianą zwykle ze średnią prędkością, wykorzystaliśmy wzór na średnią harmoniczną dwóch wielkości. Zauważ, że średnia harmoniczna w naszym przypadku była mniejsza niż średnia arytmetyczna tych samych wielkości. Czy jest tak zawsze – przedyskutuj ten problem z kolegami z klasy.
— Bardzo dziękuję za interesującą rozmowę i rozwiązanie nurtującego mnie problemu. Przy okazji uświadomiła mi też pani, że przeprowadzając sondaż należy doprecyzować zawarte w nim pytania.
Rozdział 3
Podsumowanie
Marcin podsumowuje rezultaty ankiety i rozmowy z ekspertem.
Rozmowa z naszym ekspertem zainspirowała mnie do poszukania wiadomości na temat średniej harmonicznej. W badaniach statystycznych średnia harmoniczna jest miarą położenia rozkładu, podobnie jak średnia arytmetyczna. Stosuje się ją, gdy wartości zmiennej podane są w jednostkach względnych (na przykład w km/h).
Średnią harmoniczną liczb dodatnich aIndeks dolny 11, aIndeks dolny 22, aIndeks dolny 33,…,aIndeks dolny nn obliczamy jako iloraz liczby wszystkich danych przez sumę ich odwrotności. Średnia harmoniczna n liczb jest nie większa od średniej geometrycznej i nie większa od średniej arytmetycznej tych liczb. Ze średnią harmoniczną mamy do czynienia na przykład obliczając średnią szybkość, czy dobierając oporności oporników w połączeniu równoległym. A teraz zadanie dla was. Do babci pojadę samochodem z prędkością 40 kilometrów na godzinę. Z jaką prędkością muszę wracać od babci, aby moja średnia szybkość na całej trasie była równa 48 kilometrów na godzinę?
Oblicz szybkość średnią każdego z rowerzystów, jeżeli rowerzysta A od godziny 13.00 do godziny 14.00 jechał z szybkością 15 km/h, a od godziny 14.00 do godziny 15.00 jechał z szybkością 25 km/h, rowerzysta B przez 10 km jechał z szybkością 10 km/h, a przez następne 10 km z szybkością 30 km/h, rowerzysta C godzinę jechał z szybkością 20 km/h, a przez następne 10 km jechał z szybkością 20 km/h.
Wykaż, że dla dodatnich liczb a i b
a) zachodzi nierówność
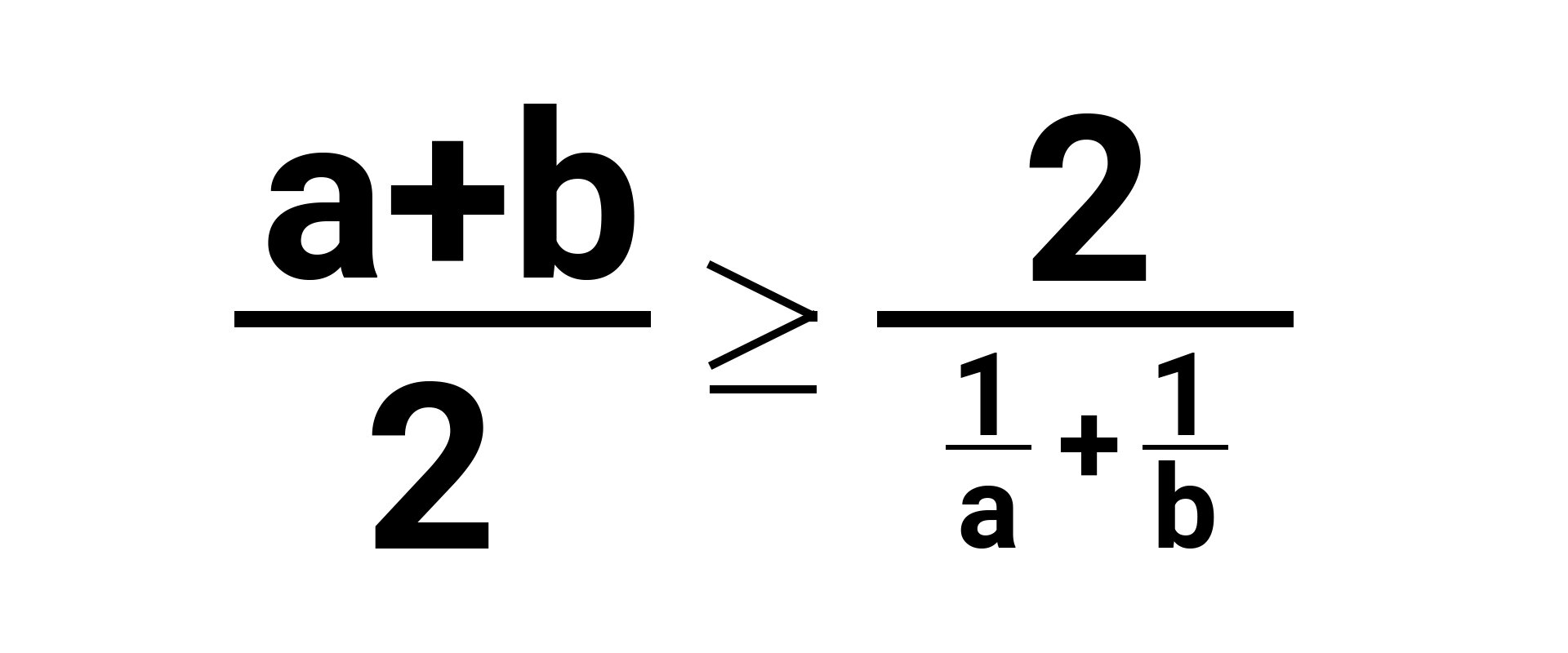
b) zachodzi nierówność

c) odwrotność średniej arytmetycznej tych liczb jest równa średniej harmonicznej odwrotności tych liczb.
Jak dobrać oporności trzech oporników o łącznym oporze 18 omega, połączonych równolegle, aby opór zastępczy był największy?
Wskazówka 1
Skorzystaj z nierówności między średnią arytmetyczną a harmoniczną.
Połączenie szeregowe

Opór zastępczy R oporów RIndeks dolny 11, RIndeks dolny 22 połączonych szeregowo, wyraża się wzorem

Połączenie równoległe

Opór zastępczy R oporów RIndeks dolny 11, RIndeks dolny 22 połączonych równolegle, wyraża się wzorem

Podsumowanie
Średnia harmonicznaŚrednia harmoniczna jest jednym z parametrów statystycznych. Stosuje się ją, gdy wartości zmiennej podane są w jednostkach względnych (np. km/h).
Średnią harmoniczną liczb dodatnich

obliczamy jako iloraz liczby wszystkich danych przez sumę ich odwrotności

Geometrycznie średnia harmoniczna to długość odcinka zawartego w trapezie, przechodzącego przez punkt przecięcia przekątnych trapezu i równoległego do postaw.
Zadanie 1.
Przeprowadź wśród uczniów twojej szkoły ankietę, w której zapytasz o średnią szybkość, z jaką poruszał się samochód, który z magazynu zawiózł ładunek do sklepu oddalonego o 100 km i powrócił tą samą trasą. Z magazynu do sklepu samochód jechał z prędkością 40 km/h, a z powrotem z prędkością 60 km/h.

Zadania
Oblicz średnią arytmetyczną poniższych liczb.
2, 10 ............
12, 10, 8 ............
5, 5, 5 ............
4, 4, 4 ............
1, 9, 8, 2 ............
0, 0, 0 ............
-10, 10 ............
-137, 137, -285, 285 ............
Oblicz średnią harmoniczną poniższych liczb. Odpowiedzi podaj w postaci ułamków nieskracalnych (do zapisu użyj prawego ukośnika).
2, 10 ............
1, 1 ............
2, 2 ............
5, 10 ............
2, 8 ............
3, 6 ............
1, 5 ............
8, 10 ............
Średnia harmoniczna liczb 8 i x wynosi 13,44. Wyznacz i wskaż x.
- 13,44
- 18,88
- 42,00
- 5,44
- 26,88
- 10,88
- 9,44
- 21,44
- 10,72
Słowniczek
Prędkość to wielkość wektorowa. W praktyce szkolnej oblicza się prędkość jako stosunek długości drogi przebytej przez ciało do czasu, w jakim ruch się odbywał.
Średnia harmoniczna liczb dodatnich

to iloraz liczby wszystkich danych przez sumę ich odwrotności.

Szybkość to wielkość skalarna. Najczęściej przyjmuje się, że jest to wartość liczbowa prędkości.
Powrót do e‑podręcznika
E‑podręcznik „Odkryj, zrozum, zastosuj...”
https://www.epodreczniki.pl/reader/c/129738/v/22/t/student-canon
3.3. Wyrażenia wymierne. Równania wymierne:
https://www.epodreczniki.pl/reader/c/129738/v/22/t/student-canon/m/iIEiNx2IIi#iIEiNx2IIi_d25e1
3.4. Zastosowanie równań wymiernych do interpretacji zagadnień praktycznych:
https://www.epodreczniki.pl/reader/c/129738/v/22/t/student-canon/m/iYcmaHaJ3L


