Zadania dotyczące kątów oraz wielokątów

Pokaż ćwiczenia:

W poniższym materiale zajmiemy się rozwiązywaniem zadań z geometrii płaskiej dotyczących różnych rodzajów kątów i ich własności oraz dotyczących wielokątów. W każdej części materiału znajdziesz krótkie przypomnienie, które pomoże Ci w rozwiązaniu ćwiczeń.

Rodzaje kątów

W tabeli poniżej znajduje się krótkie przypomnienie dotyczące różnych rodzajów kątów z uwzględnieniem ich konstrukcji i miar.

kąty wierzchołkowe	kąty przyległe	kąty odpowiadające	kąty naprzemianległe
konstrukcja
tworzą je dwie przecinające się proste	- tworzą razem kąt półpełny, - mają wspólne ramię	- tworzą je trzy proste: dwie z nich są przecięte trzecią prostą, - leżą po tej samej stronie trzeciej prostej	- tworzą je trzy proste: dwie z nich są przecięte trzecią prostą, - leżą po przeciwnej stronie trzeciej prostej
miara
mają tę samą miarę	- mają różną miarę (poza przypadkiem, gdy oba kąty są proste), - ich suma wynosi $180 °$	- jeżeli dwie przecięte proste są równoległe, to kąty odpowiadające są równe, jeżeli dwie przecięte proste nie są równoległe, to kąty odpowiadające są różne	- jeżeli dwie przecięte proste są równoległe, to kąty odpowiadające są równe, jeżeli dwie przecięte proste nie są równoległe, to kąty odpowiadające są różne

Ćwiczenie 1

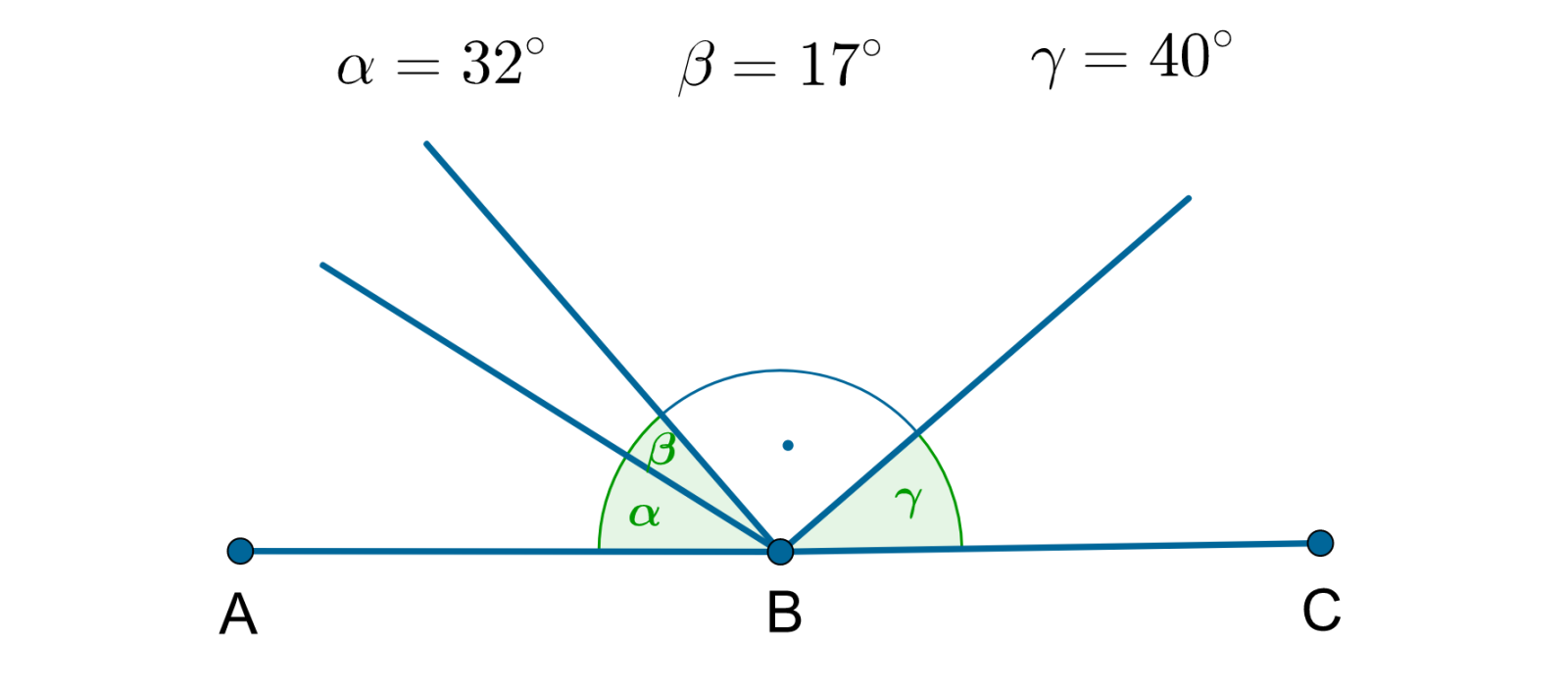
Na rysunku podane są miary kątów $α$ , $β$ , $γ$ . Czy wynika z tego, że punkty $A$ , $B$ , $C$ są współliniowe?

RG7p4ZkD8paah

Ilustracja przedstawia dwa połączone ze sobą odcinki: A B oraz A C. Punkt B jest wierzchołkiem czterech kątów. Od lewej mamy kąt alfa o mierze 32 stopnie, dalej kąt beta, który ma z nim jedno wspólne ramię. Kąt beta ma miarę 17 stopni. Dalej mamy kąt prosty, mający lewe ramię wspólne z kątem beta i prawe ramię wspólne z kątem gamma o mierze 40 stopni. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1ZtFlFWxkABY

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 2

Podaj miary kątów przy prostych równoległych.

RkXtzHFvGIDNE1

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1Vq0tbYnuluh

Jakie miary mają kąty podane poniżej? Wykorzystując odpowiednie własności, ustal miary tych kątów i wpisz je w luki. Kąty przyległe

α

β

, jeżeli: kąt

α = 20 °

, więc kąt

β =

Tu uzupełnij

°

, kąt

α = 91 °

, więc kąt

β =

Tu uzupełnij

°

, kąt

α = 111 °

, więc kąt

β =

Tu uzupełnij

°

, kąt

α = 170 °

, więc kąt

β =

Tu uzupełnij

°

. Kąty wierzchołkowe

α

β

, jeżeli: kąt

α = 50 °

, więc kąt

β =

Tu uzupełnij

°

, kąt

α = 100 °

, więc kąt

β =

Tu uzupełnij

°

, kąt

α = 1 °

, więc kąt

β =

Tu uzupełnij

°

, kąt

α = 150 °

, więc kąt

β =

Tu uzupełnij

°

. Kąty odpowiadające

α

β

(przy założeniu równoległości dwóch prostych

m

n

), jeżeli: kąt

α = 15 °

, więc kąt

β =

Tu uzupełnij

°

, kąt

α = 179 °

, więc kąt

β =

Tu uzupełnij

°

, kąt

α = 5 °

, więc kąt

β =

Tu uzupełnij

°

, kąt

α = 43 °

, więc kąt

β =

Tu uzupełnij

°

. Kąty naprzemianległe

α

β

(przy założeniu równoległości dwóch prostych

m

n

), jeżeli: kąt

α = 110 °

, więc kąt

β =

Tu uzupełnij

°

, kąt

α = 51 °

, więc kąt

β =

Tu uzupełnij

°

, kąt

α = 18 °

, więc kąt

β =

Tu uzupełnij

°

, kąt

α = 96 °

, więc kąt

β =

Tu uzupełnij

°

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 3

Na rysunku podane są miary kątów $α$ , $β$ . Czy czworokąt $A B C D$ jest równoległobokiem?

RlTWhFLCguFOs1

Na rysunku przedstawiono dwie leżące mniej więcej poziomo proste. Na górnej prostej zaznaczono od lewej punkty D oraz C, na dolnej prostej zaznaczono od lewej punkty A oraz B w taki sposób, żeby nie leżały jeden pod drugim. Następnie punkt połączono w czworokąt A B C D i oznaczono dwa kąty: kąt wewnętrzny A D C o mierze 143 stopnie oraz kąt zewnętrzny przy wierzchołku B, którego ramionami są: prawa część dolnej prostej i bok B C. Jest to kąt alfa o mierze 36 stopni. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RXJlc3pEfLVPN

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 4

Proste $k$ i $l$ są równoległe. Miary kątów $α$ , $β$ podano na rysunku. Czy wynika stąd, że $γ = 125 °$ oraz $δ = 143 °$ ?

RpN0jfW4dRy0V1

Ilustracja przedstawia dwie poziome proste, wyżej położona jest prosta l, a poniżej prosta k. Obie są przecięte przez dwie ukośne proste układające się w kształt X, przy czym punkt przecięcia ukośnych znajduje się między poziomymi prostymi. Punkt ten oznaczono literą S. Pierwsza ukośna prosta przecina prostą l w punkcie D pod kątem rozwartym gamma i przecina prostą k w punkcie B pod kątem ostrym beta równym 55 stopni. Druga ukośna prosta przecina prostą k w punkcie A pod kątem ostrym alfa równym 37 stopni i przecina prostą l w punkcie C pod kątem rozwartym sigma. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RnT5hiWZCWThf

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Zaznaczmy kąty przyległe do $α$ i do $β$ .

RVGYK0F4oxu4u1

Kąty $γ$ i $125 °$ są odpowiadające, ponieważ prosta $k$ jest równoległa do prostej $l$ , więc $γ = 125 °$ . Podobnie kąty $δ$ i $143 °$ , są odpowiadające, więc z równoległości $k$ i $l$ ,

δ = 143 °

R1LUQKVSDvHg21

Ćwiczenie 5

W trójkącie miara jednego kąta jest dwa razy większa od miary drugiego i trzy razy mniejsza od miary trzeciego kąta. Wtedy największy kąt ma miarę $120 °$ .
Miary kątów trójkąta pozostają w stosunku $1 : 2 : 3$ . Wtedy najmniejszy kąt ma miarę $20 °$ .
Kąty między jednym z boków trójkąta ostrokątnego i wysokościami opuszczonymi na pozostałe boki mają miary $35 °$ oraz $45 °$ . Kąt leżący naprzeciw tego boku ma miarę $80 °$ .
Jeden z kątów trójkąta ma miarę $50 ° .$ Miara kąta między dwusiecznymi pozostałych kątów wewnętrznych tego trójkąta jest równa $115 °$ .

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Kąty w wielokątach

Ile przekątnych ma piętnastokąt? Czy możemy łatwo obliczyć sumę miar jego kątów? Poniższa infografika zawiera kilka wybranych definicji i wzorów odpowiadających na te pytania. Sprawdź, czy je pamiętasz. Jeśli nie, kliknij w rozwijalne punkty, aby przejść do poszczególnych definicji i wzorów. Przypomnij sobie potrzebne wzory, a następnie wykonaj ćwiczenia w tej części materiału.

Ile przekątnych ma piętnastokąt? Czy możemy łatwo obliczyć sumę miar jego kątów? Poniżej przytoczono kilka wzorów odpowiadających na te pytania. Przypomnij sobie potrzebne wzory, a następnie wykonaj ćwiczenia w tej części materiału.

R2ZN8vfNADA621

Ilustracja interaktywna 1. Wielokąt to figura geometryczna, która jest częścią płaszczyzny ograniczoną pewną łamaną zwyczajną zamkniętą. Sama łamana stanowi brzeg wielokąta. Wierzchołki łamanej to wierzchołki wielokąta, natomiast boki łamanej, która wyznacza ten wielokąt, to boki wielokąta.
Przykłady:
trójkąt, romb, trapez, dziesięciokąt, deltoid, prostokąt, 2. Przekątna wielokąta to każdy odcinek, który łączący dwa wierzchołki tego wielokąta i jednocześnie nie jest bokiem figury., 3. Dwusieczna to półprosta o początku w wierzchołku kąta, dzieląca ten kąt na dwa kąty przystające, czyli o takiej samej mierze., 4.

p = n \cdot \frac{n - 3}{2}

p

- liczba przekątnych,

n

- liczba kątów wielokąta, 5.

S = α + β + γ = 180 °

,
gdzie

S

- suma kątów wewnętrznych,

α, β, γ < 180 °

- kąty wewnętrzne trójkąta, 6.

S = α + β + γ + δ = 360 °

,
gdzie

S

- suma kątów wewnętrznych,

α, β, γ, δ < 360 °

- kąty wewnętrzne czworokąta, 7.

S = (n - 2) \cdot 180 °

,
gdzie

S

- suma kątów wewnętrznych,

n

- liczba kątów wielokąta, 8.

L = a_{1} + a_{2} + \dots + a_{n - 1} + a_{n}

,
gdzie

L

- obwód,

a_{1}, a_{2}, \dots, a_{n - 1}, a_{n}

- długości kolejnych boków

n

-kąta od pierwszego boku do boku o numerze

n

, 9. Każdy

n

-kąt wypukły można podzielić na

(n - 2)

trójkątów poprzez wykreślenie wszystkich przekątnych.
Zatem suma pól tych trójkątów będzie polem

n

-kąta., 10.

P = \frac{a h}{2}

,
gdzie

a

- bok, na który upuszczono wysokość,

h

- wysokość trójkąta, 11.

P = a b

,
gdzie

a

b

- boki prostokąta,
oczywiście, gdy

a = b

, mamy kwadrat, którego pole wynosi

P = a^{2}

, 12.

P = a h

oraz

P = \frac{d_{1} \cdot d_{2}}{2}

,
gdzie

a

- bok,

h

- wysokość,

d_{1}, d_{2}

- przekątne, 13.

P = a \cdot b \cdot \sin α

oraz

P = \frac{d_{1} \cdot d_{2}}{2}

,
gdzie

a

b

- boki,

α

- kąt między bokami

a

b

d_{1}, d_{2}

- przekątne, 14.

P = \frac{(a + b) \cdot h}{2}

,
gdzie

a

b

- podstawy,

h

- wysokość, 15.

P = a \cdot h

P = a \cdot b \cdot \sin α

oraz

P = \frac{d_{1} \cdot d_{2} \cdot \sin β}{2}

,
gdzie

a

b

- boki,

α

- kąt między bokami,

d_{1}, d_{2}

- przekątne,

β

- kąt ostry między przekątnymi

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1RLIFwBsfCuT1

Ćwiczenie 6

W dziesięciokącie wypukłym suma miar kątów jest równa $1800 °$ .
W pewnym wielokącie wypukłym suma miar kątów wynosi $1620 °$ . Liczba boków tego wielokąta jest równa $11$ .
W osiemnastokącie foremnym miara kąta wewnętrznego wynosi $160 °$ .

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1JOBg1GKCj5m1

Ćwiczenie 7

W siedemnastokącie wypukłym liczba przekątnych jest równa $119$ .
Pewien wielokąt wypukły ma $35$ przekątnych. Liczba boków tego wielokąta jest równa $7$ .
Liczba przekątnych wielokąta wypukłego jest cztery razy większa od liczby jego boków. Wielokątem tym jest jedenastokąt.

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RR8Ctk4ehQAoM1

Ćwiczenie 8

Korzystając ze znanych Ci własności czworokątów oraz z własności pewnych kątów, zastanów się nad konstrukcjami opisanymi poniżej i oceń, czy są prawdziwe. Zaznacz prawda albo fałsz przy każdym ze zdań. Różnica miar dwóch sąsiednich kątów wewnętrznych równoległoboku jest równa

40 °

. Wówczas kąt rozwarty tego równoległoboku jest równy

140 °

.
prawda fałsz Różnica miar przeciwległych kątów trapezu równoramiennego wynosi

20 °

. Wówczas miara kąta wewnętrznego przy dłuższej podstawie trapezu jest równa

102 °

.
prawda fałsz Z wierzchołka kąta rozwartego równoległoboku poprowadzono dwie wysokości, które tworzą kąt o mierze

30 °

. Wtedy miara kąta ostrego tego równoległoboku wynosi

60 °

.
prawda fałsz

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1EIVS4ZowaPl1

Ćwiczenie 9

W trapezie równoramiennym

A B C D

podstawa

A B

jest dwa razy dłuższa od podstawy

C D

. Przekątna

A C

zawiera się w dwusiecznej kąta

D A B

. Pole trapezu jest równe

27 \sqrt{3}

. Na podstawie opisu oceń prawdziwość poniższych zdań, zaznaczając prawda albo fałsz. Ramię trapezu jest dwa razy dłuższe od krótszej podstawy.
prawda fałsz Długość ramienia trapezu jest równa

6

.
prawda fałsz Przekątna

A C

dzieli trapez na dwa trójkąty, z których jeden ma pole dwa razy większe od drugiego.
prawda fałsz

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1IGvN815bVdy1

Ćwiczenie 10

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RpjS5vMGUrTt11

Ćwiczenie 11

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RaUqcNTSm9HnK1

Ćwiczenie 12

z wierzchołka $D$ można poprowadzić $9$ przekątnych
wielokąt ten ma $27$ przekątnych
suma miar wszystkich kątów wewnętrznych wielokąta jest równa $1620 °$
miara kąta $ABC$ wynosi $150 °$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R6vQYCpBCdDnH2

Ćwiczenie 13

$20 °$ i $100 °$
$18 °$ i $90 °$
$21 °$ i $105 °$
$28 °$ i $80 °$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1FOUtVNGSOVc2

Ćwiczenie 14

$20 °$
$40 °$
$60 °$
$80 °$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RtffvVzvFOIOI2

Ćwiczenie 15

rozwarty
prosty
ostry, ale większy od $60 °$
mniejszy lub równy $60 °$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1EcWzdG2kk1P1

Ćwiczenie 16

$9 \sqrt{3}$
$18 \sqrt{3}$
$27 \sqrt{3}$
$54 \sqrt{3}$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RKrkWneW7ecou2

Ćwiczenie 17

$3,6$
$6$
$10$
$15$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RrEgsmyJeT80k2

Ćwiczenie 18

$30 °$
$45 °$
$60 °$
$75 °$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RPfBSkXNmB6SN2

Ćwiczenie 19

$"|"AC"|" = 2 "|"BD"|"$
$"|"∢ ABC"|" = 120 °$
pole rombu jest równe ${"|"BD"|"}^{2}$
obwód rombujest równy $2 "|"AC"|"$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 20

Na rysunku przedstawiony jest trójkąt $A B C$ . Jaka będzie miara kąta $C A B$ ?

RlroofV7DpWPf1

Rysunek trójkąta prostokątnego A B C. Kąt prosty znajduje się przy wierzchołku C. Przekątną A B przedłużono półprostą i zaznaczono za punktem B na zewnątrz trójkąta punkt D. Zaznaczono kąt zewnętrzny przy wierzchołku B między odcinkami B C oraz B D. Kąt ten ma miarę 146 stopni. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RtKdDq9lcfMd0

$"|"∢ CAB"|" = 34 °$
$"|"∢ CAB"|" = 56 °$
$"|"∢ CAB"|" = 68 °$
$"|"∢ CAB"|" = 146 °$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 21

Punkty $E$ i $F$ są środkami boków prostokąta $A B D C$ . Jaką częścią pola prostokąta jest pole trójkąta $A F E$ ?

RGF5q5kWjNZJE1

Rysunek prostokąta A B C D, w który wpisany jest trójkąt A F E. Punkt F leży w połowie boku BD a punkt E w połowie boku CD. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RD9PeEp4jWir7

$\frac{1}{2}$
$\frac{3}{8}$
$\frac{5}{8}$
$\frac{7}{8}$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RMrABpEz944x01

Ćwiczenie 22

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 23

Dany jest trapez $A B C D$ o podstawach $A B$ i $C D$ , w którym $|A D| = |D C| = 3$ .

Czy wysokość tego trapezu może być równa $4$ ? Odpowiedź uzasadnij.
Uzasadnij, że przekątna $A C$ zawiera się w dwusiecznej kąta $D A B$ .

RrKmUAT0PI0EL

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R4sobVYWmf9Z9

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Wykorzystaj fakt, że wysokość tego trapezu to przyprostokątna pewnego trójkąta prostokątnego.
Zauważ, że kąty $A C D$ i $C A B$ są tej samej miary, ponieważ są to kąty odpowiadające.

Trójkąt $A E D$ jest prostokątny. Odcinek $A D$ jest jego przeciwprostokątną, a odcinek $D E$ przyprostokątną. Przeciwprostokątna jest najdłuższym bokiem w trójkącie, stąd $|D E| < |A D|$ , czyli $|D E| < 3$ . Zatem długość odcinka $D E$ nie może być równa $4$ .
R1S4xwK3aqeAg1
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Kąty $A C D$ i $C A B$ są odpowiadające. Ponieważ proste $A B$ i $C D$ są równoległe, $|∢ A C D| = |∢ C A B|$ . Oznaczmy miarę każdego z tych kątów przez $α$ .
Trójkąt $A C D$ jest równoramienny, więc kąty przy podstawie $A C$ są sobie równe. Stąd $|∢ D A C| = α$ . Zatem prosta $A C$ jest dwusieczną kąta $D A B$ .
Rl18jh7QP6yji1
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 24

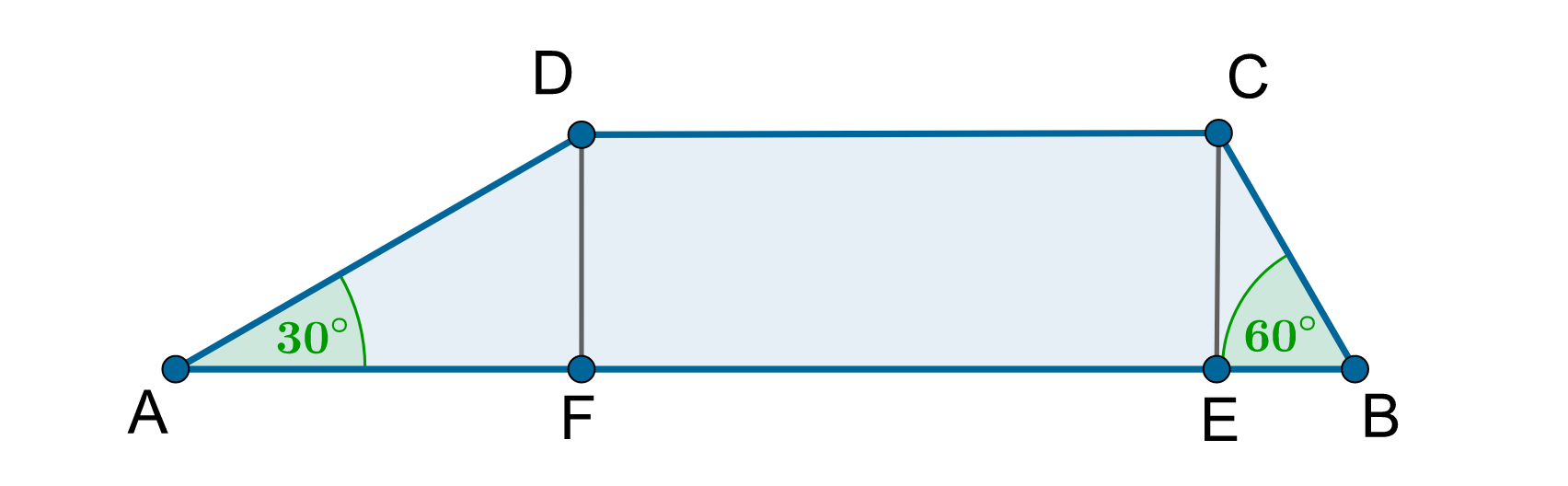
Podstawy trapezu mają długości $6$ i $10$ . Miary kątów przy dłuższej podstawie są równe $30 °$ i $60 °$ .
Oblicz pole trapezu.

R2g72zsQngY0g

Rysunek trapezu A B C D z zaznaczonymi wysokościami DF i CE. Kąt przy wierzchołku A ma miarę 30 stopni a przy B ma 60 stopni. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1JHM9jWdp5lG

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R8jyX7K4ff02r

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Oznaczmy długość odcinka $E B$ przez $x$ . Trójkąty $A F D$ oraz $C E B$ są prostokątne, a miary ich kątów ostrych są równe $30 °$ i $60 °$ . Ze związków miarowych w trójkącie $C E B$ otrzymujemy

|C E| = |D F| = x \sqrt{3}

Ze związków miarowych w trójkącie $A F D$ mamy $|A F| = 3 x$ . Podstawa $A B$ trapezu $A B C D$ ma więc długość

|A B| = 3 x + 6 + x = 10

skąd $4 x = 4$ , czyli $x = 1$ .
Wysokość $D F$ trapezu jest równa $|D F| = \sqrt{3}$ .
Pole trapezu wynosi

P = \frac{6 + 10}{2} \sqrt{3} = 8 \sqrt{3} .

Ćwiczenie 25

RzIXnUFrXRGzr

W trapezie

A B C D

poprowadzono krótszą przekątną, która podzieliła go na trójkąt prostokątny i trójkąt równoboczny. Oblicz miary kątów tego trapezu. Rozważ wszystkie przypadki. Uzupełnij luki. Kliknij w lukę, aby rozwinąć listę możliwych odpowiedzi. W każdym z rozważanych przypadków uzupełnij luki liczbami w kolejności rosnącej. 1.

60 °

, 2.

90 °

, 3.

90 °

, 4.

50 °

, 5.

45 °

, 6.

60 °

, 7.

160 °

, 8.

120 °

, 9.

120 °

, 10.

30 °

, 11.

150 °

, 12.

80 °

, 1.

60 °

, 2.

90 °

, 3.

90 °

, 4.

50 °

, 5.

45 °

, 6.

60 °

, 7.

160 °

, 8.

120 °

, 9.

120 °

, 10.

30 °

, 11.

150 °

, 12.

80 °

, 1.

60 °

, 2.

90 °

, 3.

90 °

, 4.

50 °

, 5.

45 °

, 6.

60 °

, 7.

160 °

, 8.

120 °

, 9.

120 °

, 10.

30 °

, 11.

150 °

, 12.

80 °

, 1.

60 °

, 2.

90 °

, 3.

90 °

, 4.

50 °

, 5.

45 °

, 6.

60 °

, 7.

160 °

, 8.

120 °

, 9.

120 °

, 10.

30 °

, 11.

150 °

, 12.

80 °

lub1.

60 °

, 2.

90 °

, 3.

90 °

, 4.

50 °

, 5.

45 °

, 6.

60 °

, 7.

160 °

, 8.

120 °

, 9.

120 °

, 10.

30 °

, 11.

150 °

, 12.

80 °

, 1.

60 °

, 2.

90 °

, 3.

90 °

, 4.

50 °

, 5.

45 °

, 6.

60 °

, 7.

160 °

, 8.

120 °

, 9.

120 °

, 10.

30 °

, 11.

150 °

, 12.

80 °

, 1.

60 °

, 2.

90 °

, 3.

90 °

, 4.

50 °

, 5.

45 °

, 6.

60 °

, 7.

160 °

, 8.

120 °

, 9.

120 °

, 10.

30 °

, 11.

150 °

, 12.

80 °

, 1.

60 °

, 2.

90 °

, 3.

90 °

, 4.

50 °

, 5.

45 °

, 6.

60 °

, 7.

160 °

, 8.

120 °

, 9.

120 °

, 10.

30 °

, 11.

150 °

, 12.

80 °

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

przypadek $I$
RHfMF3iMQsa2v1
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Kąt prosty $B A D$ jest sumą kątów $C A B$ oraz $C A D$ . Trójkąt $A B C$ jest równoboczny, więc wszystkie jego kąty mają miarę $60 °$ . Stąd
$|∢ C A D| = 90 ° - |∢ C A B|$ ,
czyli
$|∢ C A D| = 90 ° - 60 ° = 30 °$ .
Kąt $A C D$ ma więc miarę $60 °$ .
R6C05EHhcFu531
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Stąd miary kątów w trapezie $A B C D$ są równe: $90 °$ , $90 °$ , $120 °$ , $60 °$ .
przypadek $II$
RFSdf5hK20gup1
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Kąty $A C D$ i $B A C$ są naprzemianległe. Proste $A B$ i $C D$ są równoległe, zatem
$|∢ A C D| = |∢ B A C|$
Trójkąt $A B C$ jest równoboczny, więc wszystkie jego kąty mają miarę $60 °$ . Stąd
$|∢ A C D| = 60 °$
Otrzymujemy więc
$|∢ C D A| = 90 ° - 60 ° = 30 °$
Rr5jZ75UPt4rT1
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Miary kątów w trapezie $A B C D$ są równe: $60 °$ , $150 °$ , $30 °$ , $120 °$ .

Ćwiczenie 26

R14WA3qiZurFT

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RKB1dpGPfyKcW1

Rysunek rombu A B C D z zaznaczoną wysokością DE. Kąt przy wierzchołku A ma miarę 45 stopni. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Oznaczmy wysokość $D E$ przez $h$ . Trójkąt $A D E$ jest prostokątny, a miary jego kątów ostrych są równe $45 °$ i $45 °$ , skąd długość boku rombu $A D$ jest równa $h \sqrt{2}$ . Zatem

P = h \sqrt{2} \cdot h = h^{2} \sqrt{2}

Otrzymujemy równanie

h^{2} \sqrt{2} = 72 \sqrt{2}

Ponieważ $h > 0$ , to

h = \sqrt{72} = 6 \sqrt{2}

Długość boku rombu jest równa

6 \sqrt{2} \cdot \sqrt{2} = 12

Ćwiczenie 27

RLypMDwUCCUFy1

Rysunek trapezu prostokątnego A B C D podzielony na trzy figury: kwadrat C D E F, trójkąt B C F oraz trapez A B F E. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1VBe6lHtK5xw

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R19DUTDdhH81d1

Pole kwadratu $C D E F$ o boku $6$ jest równe $36$ . Zatem pola trapezu $A B F E$ oraz trójkąta $C F B$ także są równe $36$ .
Ze wzoru na pole trójkąta $C F B$

P_{C F B} = \frac{1}{2} |C F| \cdot |B G|

otrzymujemy

36 = \frac{1}{2} \cdot 6 \cdot |G B|

Stąd $|G B| = 12$ . Długość podstawy $AB$ jest więc równa $18$ .
Ze wzoru na pole trapezu $A B F E$ otrzymujemy

P_{A B F E} = \frac{1}{2} (|A B| + |E F|) \cdot |A E|

czyli

36 = \frac{1}{2} (18 + 6) \cdot |A E|

Stąd

|A E| = 3

Wysokość trapezu $A B C D$ jest więc równa $6 + 3 = 9$ .
Z twierdzenia Pitagorasa

|C B| = \sqrt{12^{2} + 9^{2}} = 15

Pole trapezu $A B C D$ jest równe

P_{A B C D} = \frac{1}{2} (18 + 6) \cdot 9 = 108

a jego obwód

L_{A B C D} = 18 + 15 + 6 + 9 = 48

Ćwiczenie 28

RRAaGwwQKOlVt

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Sześciokąt foremny możemy podzielić na sześć trójkątów równobocznych.

RHHg65tWSqjgg1

Rysunek sześciokąta A B C D E F z zaznaczonymi przekątnymi. Przekątne AE i AD wychodzą z wierzchołka A, pomiędzy nimi zaznaczono kąt ostry. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Szukamy miary kąta $D A E$ pomiędzy odcinkiem $D A$ , który składa się z dwóch boków trójkątów równobocznych, a odcinkiem $A E$ , który składa się z dwóch wysokości trójkąta równobocznego. Zatem kąt ten ma miarę $30 °$ .

Ćwiczenie 29

Udowodnij, że dwusieczne dwóch sąsiednich kątów równoległoboku są prostopadłe.

R7bZ6SFeQmw63

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RLxRmMyCawa1P

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Wykorzystaj fakt, że suma miar dwóch sąsiednich kątów w równoległoboku wynosi $180 °$ .

Suma miar dwóch sąsiednich kątów w równoległoboku wynosi $180 °$ , zatem jeżeli jeden kąt ma miarę $α$ , to drugi ma miarę $180 ° - α$ . Prowadzimy dwusieczne kątów.

RAWUhyZMCjEnz1

Rysunek równoległoboku A B C D wraz z poprowadzonymi dwusiecznymi kątów wychodzących z wierzchołków A i B. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Sumujemy miary kątów powstałego trójkąta.

\frac{α}{2} + 90 ° - \frac{α}{2} + x = 180 °

Stąd otrzymujemy, że $x = 90 °$ , co było do udowodnienia.