Zadania powtórkowe przed egzaminem maturalnym cz.3
Materiał zawiera zadania powtórkowe przed egzaminem maturalnym. Spróbuj je rozwiązać samodzielnie. Jeśli napotkasz problemy, możesz skorzystać z podpowiedzi zamieszczonych poniżej.
Pierwiastki:
Niech i .
Własności działań na pierwiastkach:
,
, dla ,
, dla każdego ,
, dla i .
Potęgi:
Niech , , i będą liczbami rzeczywistymi.
Własności działań na potęgach:
,
, dla ,
,
, dla ,
.
Procenty:
Procent:
Obliczanie procentu z liczby: .
Stożek i kula
Stożek:
Wzór na pole powierzchni całkowitej: .
Wzór na objętość stożka: ,
gdzie oznacza promień koła w podstawie, a oznacza wysokość stożka.
Kula:
Wzór na pole powierzchni całkowitej kuli: ,
Objętość kuli: ,
gdzie oznacza promień kuli.
Twierdzenie Pitagorasa:
,
gdzie , oznaczają długości przyprostokątnych, a długość przeciwprostokątnej.
Trójkąt równoboczny:
Wzór na pole: ,
gdzie oznacza długość boku trójkąta.
Wysokość w trójkącie równobocznym: .
Trójkąt prostokątny , i
W trójkącie prostokątnym o podanych kątach, na przeciwko kąta mamy bok długości , na przeciwko kąta mamy bok długości , a przeciwprostokątna tego trójkąta ma długość .
Średnia arytmetyczna
Średnia arytmetyczna zbioru liczb - to suma tych liczb podzielona przez ich liczbę.
Średnia arytmetyczna liczb wyraża się wzorem: .
Skala
Wymiary rzeczywiste, to skala
Skala zmniejszająca, to np. skala - wymiary zostały pomniejszone dwa razy, skala - wymiary zostały pomniejszone pięć razy.
Skala powiększająca, to np. skala - wymiary zostały powiększone dwa razy, skala - wymiary zostały powiększone trzy razy.
Graniastosłup
Jeżeli n to liczba boków figury znajdującej się w podstawie, to graniastosłup będzie miał:
ścian
krawędzi
wierzchołków
Droga, prędkość, czas
Aby wyznaczyć prędkość w kilometrach na godzinę, korzystamy ze wzoru ,
gdzie oznacza drogę podaną w kilometrach i to czas podany w godzinach.
Ostrosłup
Wzór na pole powierzchni całkowitej: ,
gdzie - pole powierzchni podstawy, - pole powierzchni bocznej.
Wzór na objętość: ,
gdzie to wysokość ostrosłupa.
Niech i .,, dla ,, dla każdego ,, dla i ., 2. Potęgi Własności działań na potęgach:
Niech , będą dodatnimi liczbami rzeczywistymi, a , dowolnymi liczbami rzeczywistymi.,,,,., 3. Procenty Procent:
.
Obliczanie procentu z liczby :
., 4. Trójkąt prostokątny , i W trójkącie prostokątnym o podanych kątach, na przeciwko kąta mamy bok długości , na przeciwko kąta mamy bok długości , a przeciwprostokątna tego trójkąta ma długość ., 5. Średnia arytmetyczna Średnia arytmetyczna zbioru liczb - to suma tych liczb podzielona przez ich liczbę. Średnia arytmetyczna liczb wyraża się wzorem: ., 6. Skala Wymiary rzeczywiste, to skala .Skala zmniejszająca, to np. skala - wymiary zostały pomniejszone dwa razy, skala - wymiary zostały pomniejszone pięć razy.Skala powiększająca, to np. skala - wymiary zostały powiększone dwa razy, skala - wymiary zostały powiększone trzy razy., 7. Trójkąt równoboczny
Wzór na pole: .
Wysokość w trójkącie równobocznym : ,
gdzie oznacza długość boku trójkąta., 8. Twierdzenie Pitagorasa
,
gdzie , oznaczają długości przyprostokątnych, a długość przeciwprostokątnej., 9. Stożek i kula
Stożek :
Wzór na pole powierzchni całkowitej stożka: ,
gdzie oznacza promień koła w podstawie, a tworzącą stożka.
Objętość stożka: ,
gdzie oznacza wysokość stożka.
Kula :
Wzór na pole powierzchni całkowitej kuli:
Objętość kuli: .
oznacza promień kuli., 10. Droga, prędkość, czas Aby wyznaczyć prędkość w kilometrach na godzinę, korzystamy ze wzoru ,
gdzie oznacza drogę podaną w kilometrach, a czas podany w godzinach., 11. Graniastosłup Jeżeli n to liczba boków figury znajdującej się w podstawie, to graniastosłup będzie miał:
ścian
krawędzi
wierzchołków, 12. Ostrosłup Wzór na pole powierzchni całkowitej:
,
gdzie - pole powierzchni podstawy, - pole powierzchni bocznej.
Wzór na objętość: ,
gdzie to wysokość ostrosłupa.
- lat
- lat
- lata
- lat
Liczby te uporządkowane od największej do najmniejszej to Możliwe odpowiedzi: 1. , , , , 2. , , , , 3. , , , , 4. , , ,
, , , jest prawdziwych? Możliwe odpowiedzi: 1. jedna, 2. dwie, 3. trzy, 4. cztery
- jedna
- dwie
- trzy
- cztery
Czwarta część liczby jest równa: Możliwe odpowiedzi: 1. , 2. , 3. , 4.
Oceń, czy poniższe zdania są prawdziwe czy fałszywe. Zaznacz zdanie prawdziwe. Możliwe odpowiedzi: 1. Karol musiałby wylosować losów, aby mieć pewność, że wśród nich jest przynajmniej jeden los wygrywający., 2. Prawdopodobieństwo wylosowania losu przegrywającego jest dwa razy większe niż prawdopodobieństwo wylosowania losu wygrywającego.
Para liczb i jest rozwiązaniem układu równań: Możliwe odpowiedzi: 1. , 2. , 3. , 4.
- i
- i
- i
- 6 i
O ile większa była prędkość, z jaką turysta schodził ze szczytu od tej, z którą wchodził na szczyt? Wybierz odpowiedź spośród podanych. Możliwe odpowiedzi: 1. o , 2. o , 3. o , 4. o
- o
- o
- o
- o
Na wykresie przedstawiono, jak zmieniała się cena akcji pewnej firmy od stycznia do grudnia.
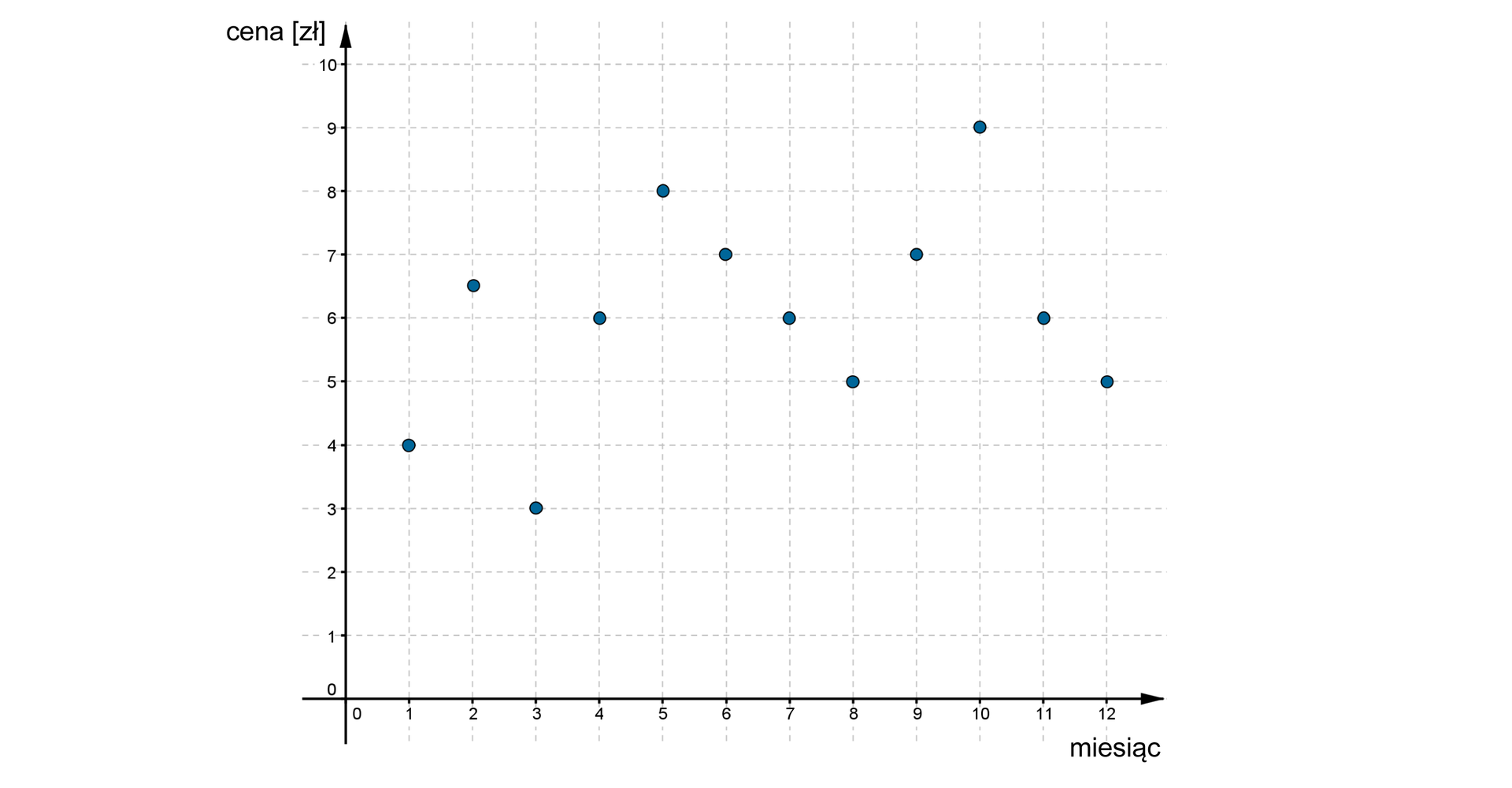
Zaznacz poprawne dokończenie zdania.
Sprzedając kupionych akcji we wrześniu, a pozostałe akcje w październiku pan Grzegorz Możliwe odpowiedzi: 1. zarobił ., 2. zarobił ., 3. stracił ., 4. stracił .
- zarobił
- zarobił
- stracił
- stracił
Oceń, czy poniższe zdania są prawdziwe czy fałszywe. Zaznacz wszystkie zdania prawdziwe. Możliwe odpowiedzi: 1. Funkcja nie przyjmuje wartości ujemnych, 2. Punkt o współrzędnych należy do wykresu funkcji, 3. Punkt o współrzędnych nie należy do wykresu funkcji, 4. Funkcja przyjmuje wartości ujemne
- Funkcja nie przyjmuje wartości ujemnych.
- Punkt o współrzędnych należy do wykresu funkcji.
Pole kwadratu jest równe .
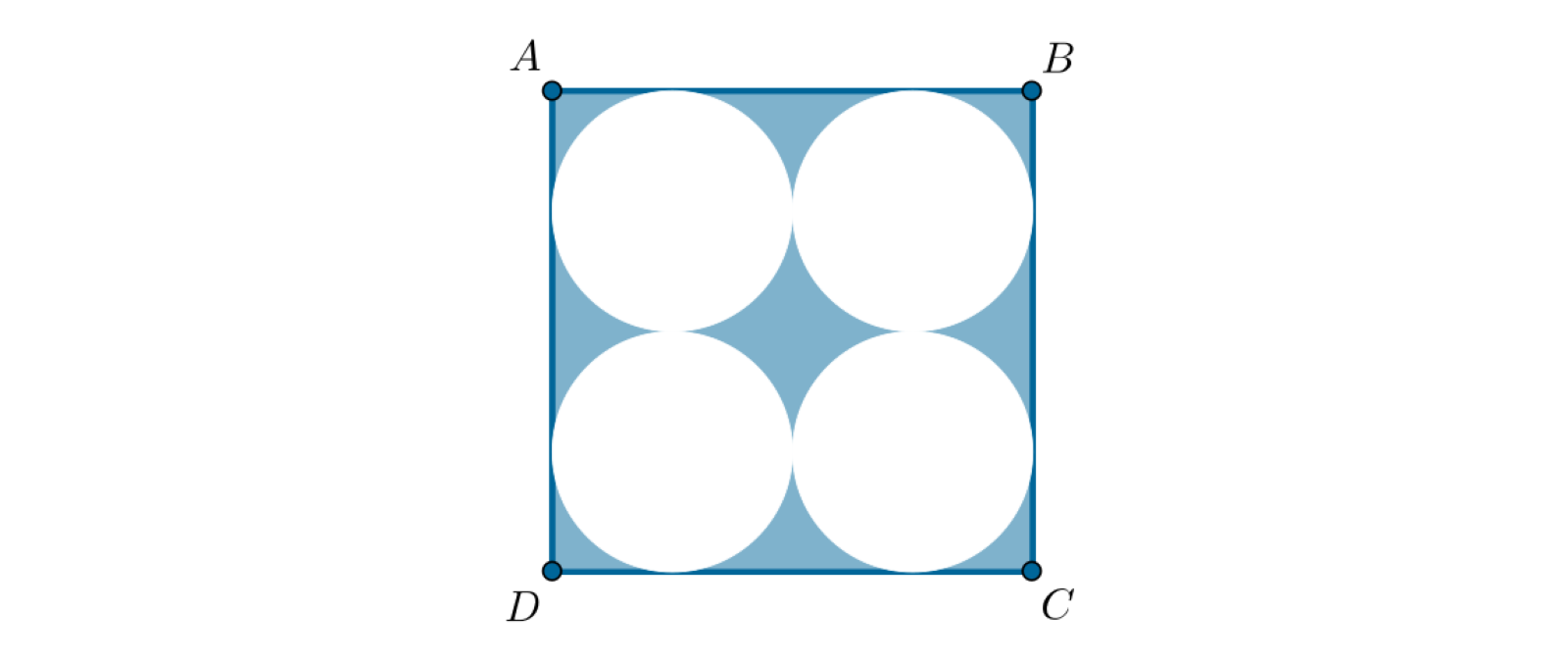
Oceń, czy poniższe zdania są prawdziwe czy fałszywe. Zaznacz wszystkie zdania prawdziwe. Możliwe odpowiedzi: 1. Wysokość tego trójkąta jest równa ., 2. Dwusieczne kątów tego trójkąta przecinają się w punkcie odległym od każdego z wierzchołków o ., 3. Dwusieczne kątów tego trójkąta przecinają się w punkcie odległym od każdego z wierzchołków o ., 4. Wysokość tego trójkąta jest równa .
- Wysokość tego trójkąta jest równa .
- Dwusieczne kątów tego trójkąta przecinają się w punkcie odległym od każdego z wierzchołków o .
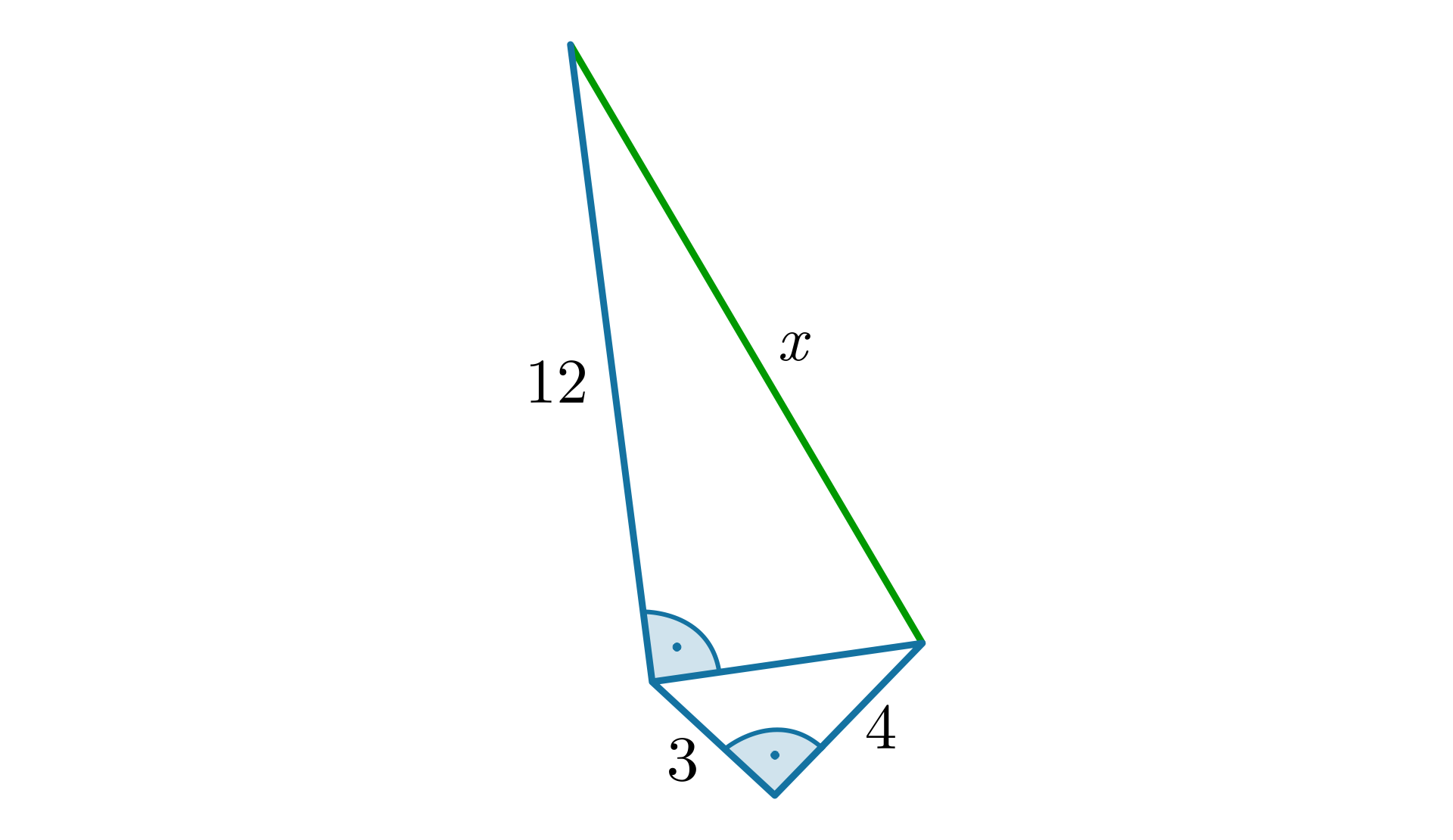
Przekątne prostokąta długości przecinają się pod kątem .
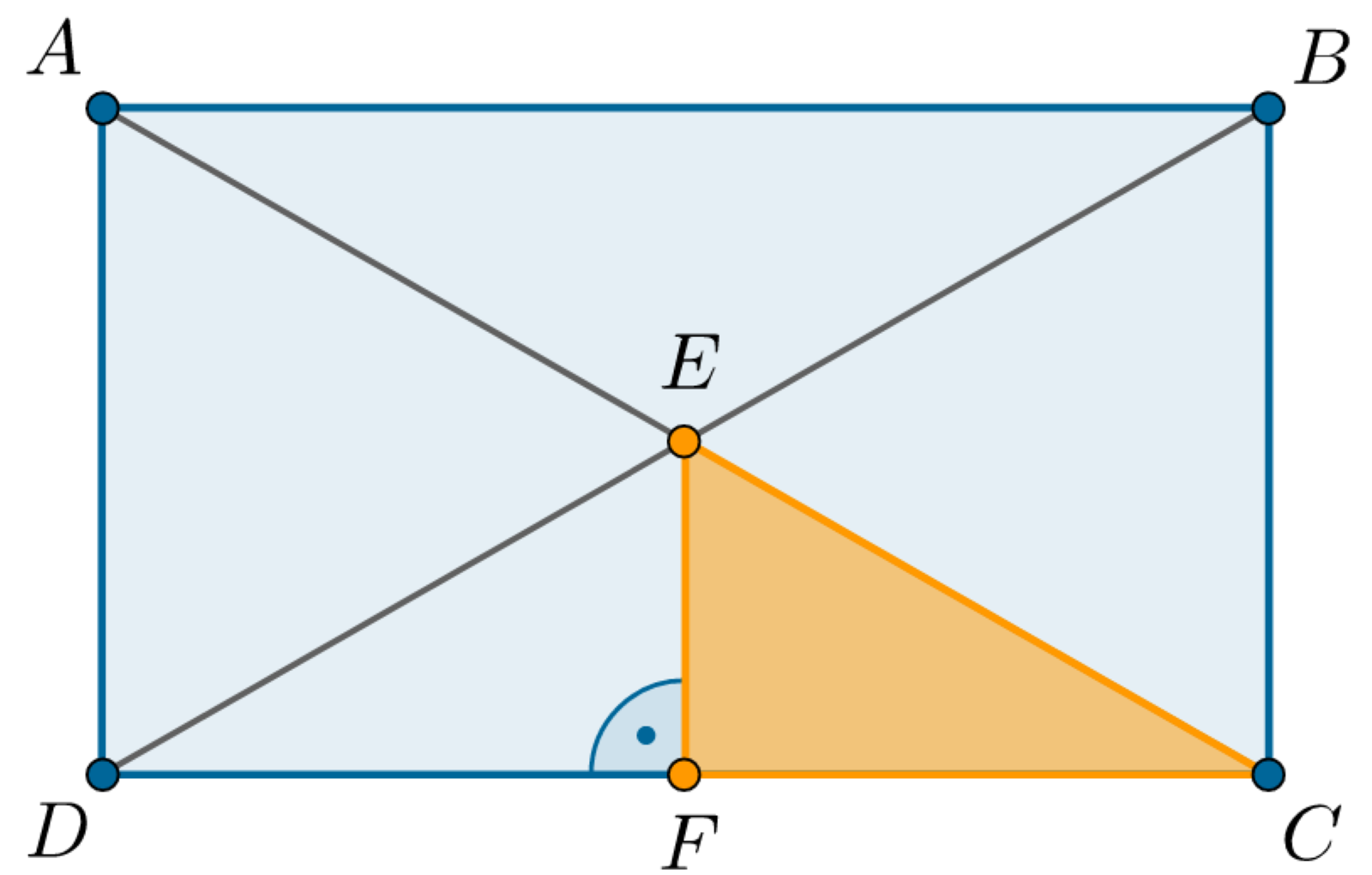
Pole powierzchni bocznej stożka jest równe Możliwe odpowiedzi: 1. , 2. , 3. , 4.
Uzasadnij, że jeśli w liczbie trzycyfrowej cyfra dziesiątek jest równa sumie cyfr jedności i setek, to ta liczba jest podzielna przez .
Rysunek przedstawia siatkę ostrosłupa prawidłowego.
