Zadania tekstowe prowadzące do równań kwadratowych - przykłady
W tym materiale zawarte są przykłady rozwiązywania zadań tekstowych przy pomocy równań kwadratowych. Jeżeli chcesz sobie przypomnieć w jaki sposób rozwiązuje się równania kwadratowe, zajrzyj do materiału Równanie kwadratoweRównanie kwadratowe.
Pokażemy teraz kilka przykładowych zadań tekstowych, w których interpretacja danych zapisanych w ich treści doprowadzi do równania kwadratowego.
W roku na uroczystości urodzin zapytano jubilata, ile ma lat. Jubilat odpowiedział: „Jeśli wiek, który osiągnę za lat pomnożę przez wiek, który osiągnę za lat, to otrzymam rok mojego urodzenia”. W którym roku urodził się ten jubilat?

Film dostępny pod adresem /preview/resource/R49aW2X3CDHj9
Animacja przedstawia przykładowe zadanie tekstowe, które możemy rozwiązać przy pomocy równania kwadratowego.
Odpowiedź: Jubilat urodził się w roku.
Liczba wszystkich przekątnych pewnego wielokąta foremnego jest równa . Ile boków ma ten wielokąt?
Oznaczmy liczbę boków wielokąta przez . Wówczas liczba jego przekątnych jest równa .
Otrzymujemy równanie
Stąd
Obliczamy wyróżnik
Wobec tego równanie ma dwa rozwiązania, którymi są oraz .
Drugie z rozwiązań odrzucamy, gdyż liczba boków nie może być ujemna. Zatem ten wielokąt jest osiemnastokątem.
Odpowiedź: Ten wielokąt ma osiemnaście boków.
Pole powierzchni bocznej prostopadłościanu o podstawie kwadratowej jest równe . Krawędź podstawy jest o krótsza od krawędzi bocznej. Oblicz objętość tego prostopadłościanu.
Oznaczmy przez długość krawędzi podstawy prostopadłościanu. Wtedy długość jego krawędzi bocznej jest równa , a pole powierzchni bocznej jest równe . Otrzymujemy równanie
Stąd:
Obliczamy wyróżnik
Wobec tego równanie ma dwa rozwiązania, którymi są
oraz .
Tylko pierwsze z nich spełnia warunki zadania, co oznacza, że jest to prostopadłościan o wymiarach , i , a więc jego objętość jest równa .
Odpowiedź: .
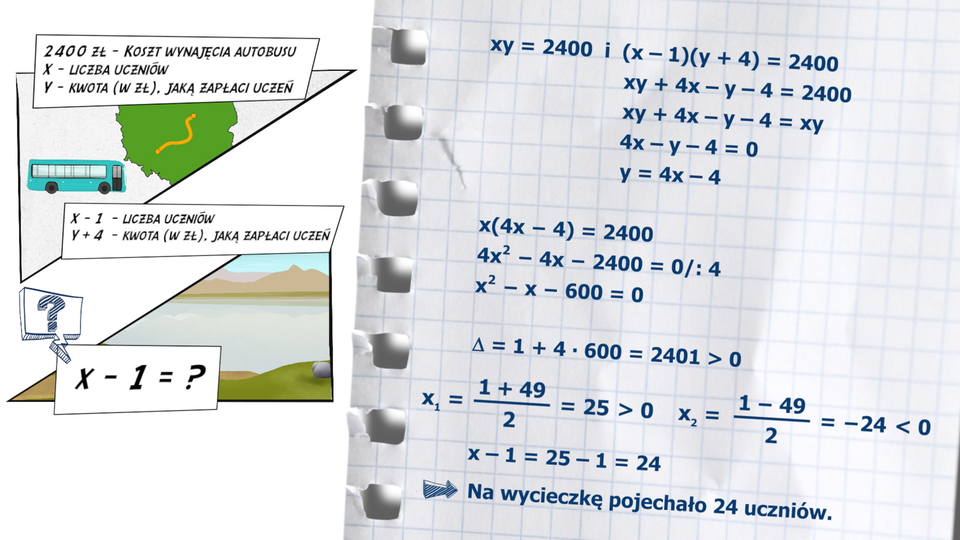
Film dostępny pod adresem /preview/resource/Ro9lOrgUamB7y
Animacja przedstawia przykładowe zadanie tekstowe z dwiema niewiadomymi, które możemy rozwiązać przy pomocy równania kwadratowego.
Geodeta wytyczył teren pod dwie prostokątne działki. Pierwsza działka ma pole powierzchni . Druga działka ma długość o większą i szerokość o większą niż pierwsza oraz pole powierzchni większe o . Obliczymy wymiary obu działek.
Wprowadzamy oznaczenia:
– długość pierwszej działki (w metrach),
– szerokość pierwszej działki (w metrach).
Ponieważ jej pole powierzchni jest równe , więc .
Wtedy druga działka ma wymiary:
długość: oraz szerokość: ,
a skoro jej pole powierzchni jest równe , więc
Uwzględniamy w tym równaniu zależność i przekształcamy je do postaci
Stąd:
Obliczamy wyróżnik:
Równanie ma więc dwa rozwiązania, którymi są oraz .
Zatem możliwe są dwa przypadki:
pierwsza działka ma wymiary i i wtedy druga ma wymiary i lub pierwsza działka ma wymiary i i wtedy druga ma wymiary i
.
Odpowiedź: Możliwe są dwa rozwiązania: pierwsza działka ma wymiary i
, druga – i lub pierwsza działka ma wymiary i , druga – i .