Zadania tekstowe prowadzące do równań kwadratowych

Materiał zawiera przykłady problemów, które można rozwiązać, wykorzystując wzór na długość drogi przebytej przez ciało poruszające się ze stałą prędkością w określonym czasie. Rozwiązując zamieszczone tu ćwiczenia, wykorzystasz zdobytą wiedzę w zadaniach tekstowych z kontekstem realistycznym.

Przykład 1

Zapoznaj się z poniższą animacją.

R18cBm6J1c4L61

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Rozwiążemy teraz trzy przykładowe zadania dotyczące zagadnień związanych z drogą oraz prędkością i czasem.

Przykład 2

Pociąg towarowy miał przebyć pewną drogę w czasie $21$ godzin. W połowie drogi pociąg niespodziewanie zatrzymano na pół godziny. Aby uniknąć spóźnienia, pozostałą część trasy pociąg przebył ze średnią prędkością o $2 \frac{km}{h}$ większą niż planowana. Jaka była długość tej drogi i planowana prędkość pociągu?

Oznaczmy planowaną prędkość pociągu przez $x (\frac{km}{h})$ . Zatem przez pierwsze $10,5$ godziny jazdy pociąg pokonał połowę drogi, czyli $(10, 5 \cdot x) km$ . Po nieplanowanym postoju jechał jeszcze przez $10$ godzin z prędkością $(x + 2) \frac{km}{h}$ , pokonując wtedy drugą połowę drogi, czyli $10 (x + 2) km$ .

Wówczas $10, 5 \cdot x = 10 (x + 2)$ , a stąd $x = 40$ . Oznacza to, że pociąg przejechał $840 km$ , a planowana średnia prędkość jazdy to $40 \frac{km}{h}$ .

Przykład 3

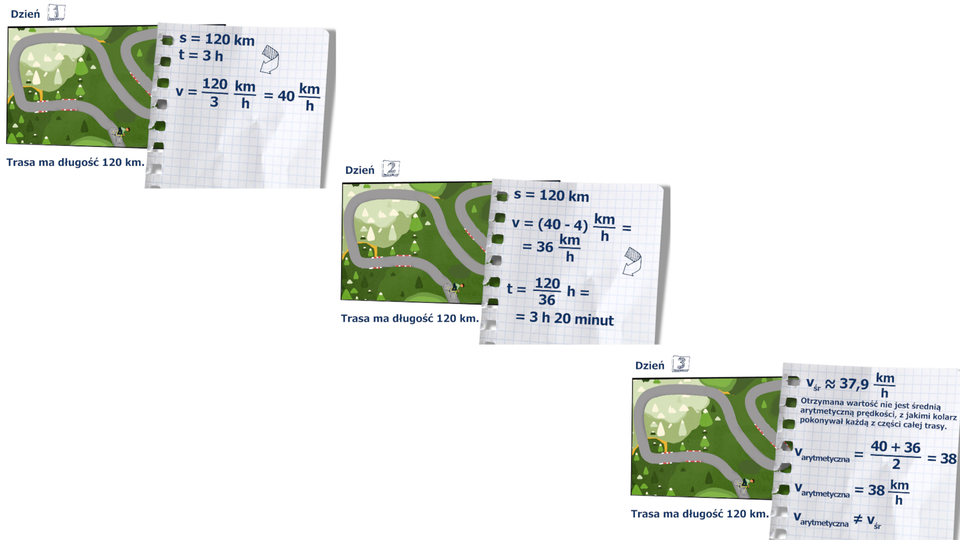
Pewien rowerzysta przebył zaplanowaną trasę o długości $200 km$ , pokonując w ciągu każdej godziny jazdy tę samą liczbę kilometrów. Gdyby rowerzysta mógł przeznaczyć na tę wyprawę o $2$ godziny więcej, to w ciągu każdej godziny mógłby przejeżdżać o $5 km$ mniej. Obliczymy, z jaką średnią prędkością jechał ten rowerzysta.

Wprowadzamy oznaczenia:

$x$ – czas (w godzinach) jazdy rowerzysty na trasie $200 km$ ,

$y$ – wartość średniej prędkości (w $\frac{km}{h}$ ), z jaką jechał.

Wtedy

x y = 200

Gdyby rowerzysta jechał przez $(x + 2)$ godziny, to jego średnia prędkość na trasie $200 km$ byłaby równa $(y - 5) \frac{km}{h}$ .

Zatem

(x + 2) (y - 5) = 200

Uwzględniamy w tym równaniu zależność $x y = 200$ i przekształcamy je do postaci

y = \frac{5 x + 10}{2}

Stąd

\frac{5 x + 10}{2} \cdot x = 200

5 x^{2} + 10 x = 400

x^{2} + 2 x - 80 = 0

Obliczamy wyróżnik $Δ = 2^{2} - 4 \cdot 1 \cdot (- 80) = 324 = 18^{2}$ . Równanie ma więc dwa rozwiązania, którymi są $x_{1} = \frac{- 2 + 18}{2} = 8$ , $x_{2} = \frac{- 2 - 18}{2} = - 10$ .

Drugie z rozwiązań odrzucamy, gdyż czas nie może być ujemny.

Zatem rowerzysta przejechał trasę $200 km$ w czasie $8$ godzin, co oznacza, że jechał ze średnią prędkością $25 \frac{km}{h}$ .

Odpowiedź: $25 \frac{km}{h}$

Przykład 4

Miasta $A$ i $B$ są oddalone o $400 km$ . Pan Stanisław pokonał tę trasę samochodem w czasie o $75$ minut krótszym niż pan Zenon. Wartość średniej prędkości, z jaką jechał pan Stanisław na całej trasie była o $16 \frac{km}{h}$ większa od wartości średniej prędkości, z jaką jechał pan Zenon.

Oblicz średnie wartości:

prędkości, z jaką pan Stanisław jechał z $A$ do $B$ ,
prędkości, z jaką pan Zenon jechał z $A$ do $B$ .

Wprowadzamy oznaczenia:

$x$ – czas jazdy pana Zenona,

$y$ – wartość średniej prędkości (w $\frac{km}{h}$ ), z jaką jechał pan Zenon.

Wtedy

x y = 400

Pan Stanisław przebył drogę z $A$ do $B$ w czasie $(x - \frac{75}{60})$ godziny, a średnia wartość jego prędkości była równa $(y + 16) \frac{km}{h}$ .

Zatem

(x - \frac{75}{60}) (y + 16) = 400

Uwzględniamy w tym równaniu zależność $x y =400$ i przekształcamy je do postaci $- \frac{5}{4} y + 16 x - 20 = 0$ .

Stąd

y = \frac{64}{5} x - 16

co oznacza, że

(\frac{64}{5} x - 16) \cdot x = 400

\frac{64}{5} x^{2} - 16 x - 400 = 0

4 x^{2} - 5 x - 125 = 0

Obliczamy wyróżnik $Δ = {(- 5)}^{2} - 4 \cdot 4 \cdot (- 125) = 2025 = 45^{2}$ .

Równanie ma więc dwa rozwiązania $x_{1} = \frac{5 + 45}{8} = \frac{25}{4}$ , $x_{2} = \frac{5 - 45}{8} = - 5$ .

Drugie z rozwiązań odrzucamy, gdyż czas nie może być ujemny.

Zatem pan Zenon przejechał trasę $400 km$ w czasie $6$ godzin $15$ minut, co oznacza, że jechał ze średnią prędkością $64 \frac{km}{h}$ . Wtedy średnia wartość prędkości, z jaką jechał pan Stanisław była równa $80 \frac{km}{h}$ .

Odpowiedź: Średnia wartość prędkości, z jaką pan Stanisław jechał z $A$ do $B$ :
$80 \frac{km}{h}$ , średnia wartość prędkości, z jaką pan Zenon jechał z $A$ do $B$ : $64 \frac{km}{h}$ .

Ćwiczenie 1

RNG8yFlIEPXqy

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Szkic rozwiązania. Oznaczamy mniejszą z tych liczb przez $x$ , stąd druga to $x + 1$ . Otrzymujemy równanie $x^{2} + {(x + 1)}^{2} = 685$ , które ma dwa rozwiązania $x_{1} = 18$ i $x_{2} = - 19$ .

Ćwiczenie 2

R1ZVUj9fLVFLW

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Szkic rozwiązania. Oznaczamy liczbę boków wielokąta przez $n$ . Wtedy liczba jego przekątnych to $\frac{n (n - 3)}{2}$ .

Otrzymujemy równanie $n + \frac{n (n - 3)}{2} = 210$ , które ma dwa rozwiązania $n_{1} = 21$ i $n_{2} = - 20$ . Drugie z tych rozwiązań odrzucamy.

Ćwiczenie 3

R1CAsenE1P5ei

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Szkic rozwiązania. Oznaczamy długość krawędzi podstawy prostopadłościanu przez $x$ . Wtedy krawędź boczna ma długość $4 x - 1$ .

Otrzymujemy równanie $2 x^{2} + 4 x (4 x - 1) = 272$ , które ma dwa rozwiązania $x_{1} = 4$ oraz $x_{2} = - \frac{34}{9}$ . Drugie z tych rozwiązań odrzucamy.

Ćwiczenie 4

RpJQgOGdKX6Xg

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Szkic rozwiązania. Oznaczamy liczbę zakupionych teczek przez $x$ , a cenę jednej teczki przez $y$ (w złotych).

Otrzymujemy równania $x y = 435$ oraz $(x + 10) (y - 0,05) = 435$ , stąd $x y + 10 y - \frac{1}{20} x - \frac{1}{2} = 435$ . Uwzględniając $x y = 435$ , otrzymujemy
$y = \frac{1}{200} x + \frac{1}{20}$ , stąd $x \cdot (\frac{1}{200} x + \frac{1}{20}) = 435$ , a więc $x^{2} + 10 x - 87 000 = 0$ . To równanie ma dwa rozwiązania $x_{1} = 290$ i $x_{2} = - 300$ . Drugie z tych rozwiązań odrzucamy.

Ćwiczenie 5

R1LHA3EbEuHYw

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Szkic rozwiązania. Oznaczamy przez $x$ – liczbę kopert produkowanych w ciągu minuty przez ten automat, a przez $y$ – czas pracy (w minutach). Otrzymujemy równania $x y = 7200$ oraz $(x + 8) (y - 30) = 7200$ , stąd $x y - 30 x + 8 y - 240 = 7200$ . Uwzględniając $x y = 7200$ , otrzymujemy $y = \frac{15}{4} x + 30$ , stąd $x \cdot (\frac{15}{4} x + 30) = 7200$ . Zatem $x^{2} + 8 x - 1920 = 0$ . To równanie ma dwa rozwiązania $x_{1} = 40$ i $x_{2} = - 48$ . Drugie z tych rozwiązań odrzucamy.

Ćwiczenie 6

RLZvbnSG9KVsb

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Szkic rozwiązania. Oznaczamy przez $x$ – średnią prędkość samochodu, przez $y$ – czas, w którym samochód pokonał $240 km$ . Otrzymujemy równania $x y = 240$ oraz $(x + 12) (y - 1) = 240$ , stąd $x y + 12 y - x - 12 = 240$ . Uwzględniając $x y = 240$ , otrzymujemy $x = 12 y - 12$ . Zatem $(12 y - 12) \cdot y = 240$ , co oznacza, że $y^{2} - y - 20 = 0$ . To równanie ma dwa rozwiązania $y_{1} = 5$ i $y_{2} = - 4$ . Drugie z tych rozwiązań odrzucamy.

Ćwiczenie 7

R1SWKaECgsV13

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Szkic rozwiązania. Oznaczamy przez $x$ – średnią prędkość samochodu, przez $y$ – czas, w którym samochód pokonał $210 km$ . Otrzymujemy równania $x y = 210$ oraz $(x + 10) (y - \frac{42}{60}) = 210$ , stąd $x y + 10 y - \frac{7}{10} x - 7 = 210$ . Uwzględniając
$x y = 210$ , otrzymujemy $y = \frac{7}{100} x + \frac{7}{10}$ . Zatem $(\frac{7}{100} x + \frac{7}{10}) \cdot x = 210$ , co oznacza, że $x^{2} + 10 x - 3000 = 0$ . To równanie ma dwa rozwiązania $x_{1} = - 60$ i $x_{2} = 50$ . Pierwsze z tych rozwiązań odrzucamy.

Ćwiczenie 8

RbqNrWrn5AytL

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Szkic rozwiązania. Oznaczamy przez $x$ – średnią prędkość rowerzysty, przez $y$ – czas, w którym rowerzysta pokonał $72 km$ . Otrzymujemy równania $x y = 72$ oraz $(x + 6) (y - \frac{36}{60}) = 72$ , skąd $x y + 6 y - \frac{3}{5} x - \frac{18}{5} = 72$ . Uwzględniając $x y = 72$ , otrzymujemy $y = \frac{1}{10} x + \frac{3}{5}$ . Zatem $x \cdot (\frac{1}{10} x + \frac{3}{5}) = 72$ , co oznacza, że $x^{2} + 6 x - 720 = 0$ . To równanie ma dwa rozwiązania $x_{1} = 24$ oraz $x_{2} = - 30$ . Drugie z tych rozwiązań odrzucamy.

Ćwiczenie 9

RoSYPG2qfZmmu

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Oznaczamy przez $x$ – planowaną średnią prędkość rowerzysty, przez $y$ – czas, w którym pokonał on pierwsze $60 km$ . Otrzymujemy równania $x y = 60$ oraz $(x + 6) (4,5 - y) = 60$ , stąd $4, 5 x - 6 y + 27 - x y = 60$ . Uwzględniając $x y = 60$ , otrzymujemy $4, 5 x - 6 y - 93 = 0$ . Zatem $(\frac{4}{3} y + \frac{62}{3}) \cdot y = 60$ , co oznacza, że $2 y^{2} + 31 y - 90 = 0$ . To równanie ma dwa rozwiązania $y_{1} = 2, 5$ i $y_{2} = - 18$ . Drugie z tych rozwiązań odrzucamy.

Ćwiczenie 10

RGZTYJydm5i43

W miasteczku są dwa place zabaw w kształcie prostokątów. Przekątna każdego z tych prostokątów jest równa

85 m

. Drugi plac ma długość o

7 m

większą niż pierwszy, ale szerokość o

11 m

mniejszą. Uzupełnij zdania, przeciągając w luki odpowiednie wymiary lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. Odpowiedź: Pierwszy plac miał wymiary 1.

51 m \times 68 m

, 2.

60 m \times 35 m

, 3.

80 m \times 20 m

, 4.

75 m \times 40 m

. Drugi plac miał wymiary 1.

51 m \times 68 m

, 2.

60 m \times 35 m

, 3.

80 m \times 20 m

, 4.

75 m \times 40 m

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Szkic rozwiązania. Oznaczamy przez $x$ i $y$ odpowiednio długość i szerokość pierwszego placu zabaw.

Korzystając z twierdzenia Pitagorasa, otrzymujemy równania $x^{2} + y^{2} = 85^{2}$ oraz ${(x + 7)}^{2} + {(y - 11)}^{2} = 85^{2}$ , stąd $x^{2} + 14 x + 49 + y^{2} - 22 y + 121 = 85^{2}$ . Uwzględniając $x^{2} + y^{2} = 85^{2}$ , otrzymujemy $y = \frac{7}{11} x + \frac{85}{11}$ .

Zatem $x^{2} + {(\frac{7}{11} x + \frac{85}{11})}^{2} = 85^{2}$ , co oznacza, że $x^{2} + 7 x - 5100 = 0$ . To równanie ma dwa rozwiązania $x_{1} = 68$ i $x_{2} = - 75$ . Drugie z tych rozwiązań odrzucamy.