Zapisywanie wyrażeń dwumianowanych w postaci liczb dziesiętnych i odwrotnie
W tym materiale dowiesz się, jak zapisujemy wyrażenia dwumianowane w postaci ułamków dziesiętnych i odwrotnie, jak wielkości zapisane z użyciem postaci dziesiętnej zapisujemy jako wyrażenia dwumianowane. Aby dokładnie zrozumieć to zagadnienie, na początku, przypomnimy podstawowe informacje o ułamkach dziesiętnych.
Ułamki i liczby dziesiętne
Film dostępny pod adresem /preview/resource/RZpx9ukpSB1EX
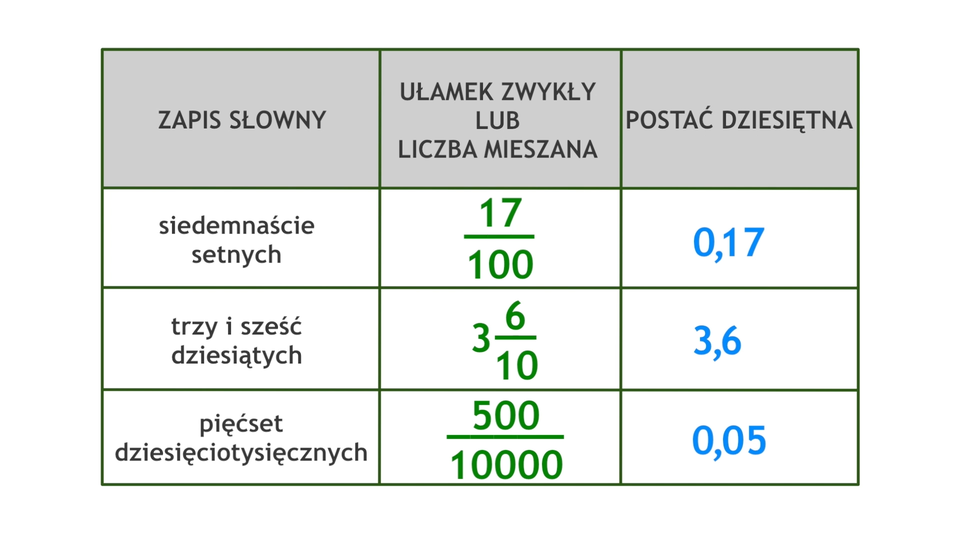
Animacja przedstawia zapis różnych liczb w postaci ułamka zwykłego lub liczby mieszanej i w postaci dziesiętnej.
Odczytaj, jaką część kwadratu zamalowano.
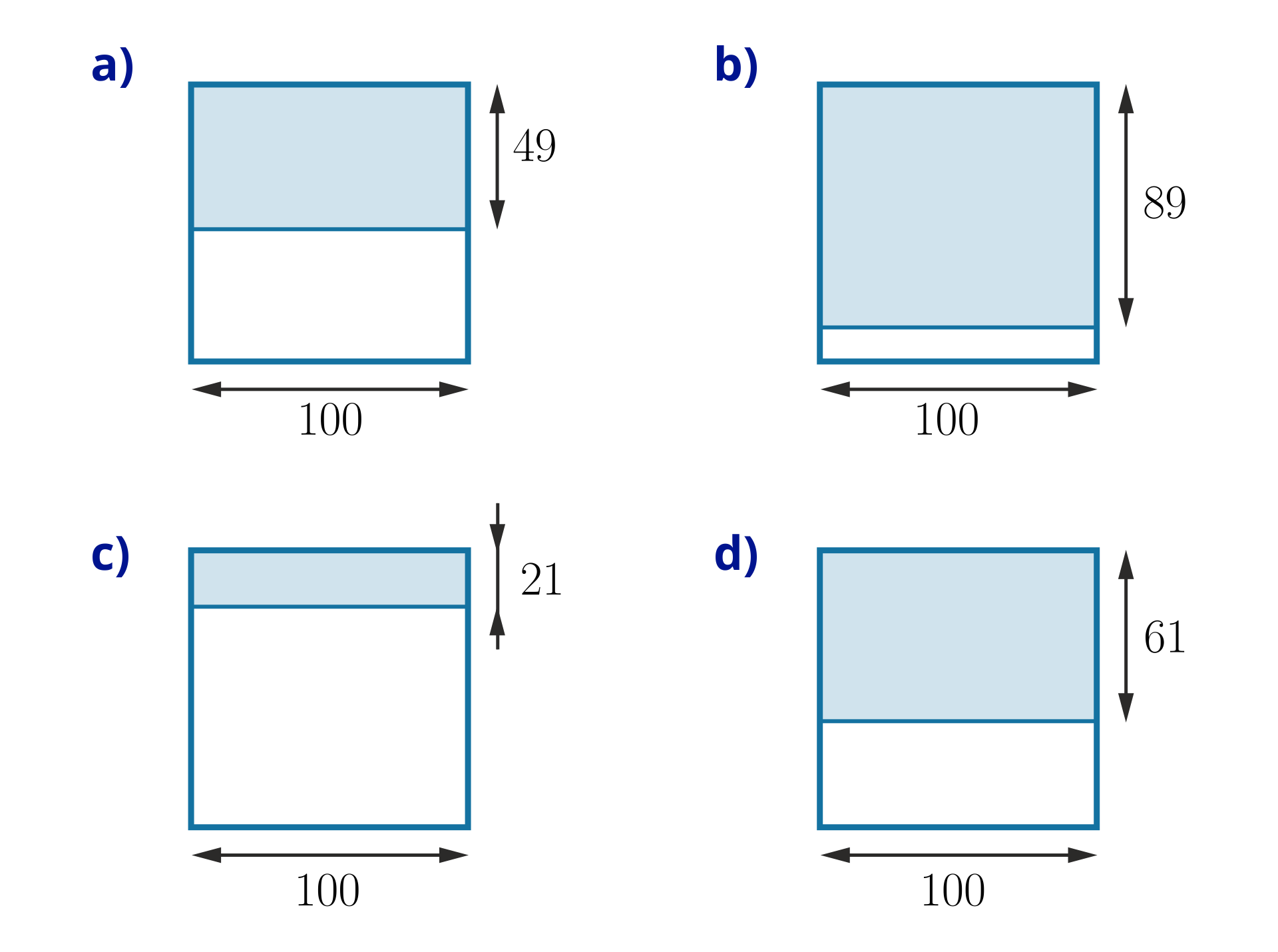
Uzupełnij liczniki ułamków.
Jeżeli , to ............
Jeżeli , to ............
Jeżeli , to ............
Jeżeli , to ............
Uzupełnij mianowniki ułamków.
a) Jeżeli , to ............
b) Jeżeli , to ............
c) Jeżeli , to ............
d) Jeżeli , to ............
Zapisz ułamki w postaci dziesiętnej.
a) ............
b) ............
c) ............
d) ............
e) ............
f) ............
g) ............
h) ............
Wyrażenia dwumianowane i liczby dziesiętne
Wyrażenia dwumianowane to wyrażenia, w których występują dwie jednostki tego samego typu, np. , i .
Obejrzyj poniższy film prezentujący zapisywanie różnych wielkości za pomocą wyrażeń dwumianowanych i liczb dziesiętnych.

Film dostępny pod adresem /preview/resource/RJ1gPmmKhzV62
Animacja pokazuje jak wyrażenie dwumianowe możemy zapisać przy pomocy liczby dziesiętnej.
Zapisz podaną wielkość używając liczb dziesiętnych.
Rozwiązanie:
Ponieważ , to .
Ułamek możemy zapisać w postaci dziesiętnej, wtedy .
Więc .
Zapisujemy nasze wyrażenie:
to
Rozwiązanie:
Ponieważ , to .
Oznacza to, że .
Zapisujemy nasze wyrażenie:
to .
Rozwiązanie:
Ponieważ , to ,
więc .
Zapisujemy nasze wyrażenie: .
Zapisz podane kwoty, używając liczb dziesiętnych.
a) 1 zł 24 gr = ............ zł
b) 3 zł 15 gr = ............ zł
c) 7 zł 20 gr = ............ zł
d) 10 zł 2 gr = ............ zł
e) 23 zł 1 gr = ............ zł
f) 83 zł 90 gr = ............ zł
Zapisz podane kwoty, używając liczb dwumianowanych.
a) 30,01 zł = ............ zł ............ gr
b) 68,28 zł = ............ zł ............ gr
c) 10,9 zł = ............ zł ............ gr
d) 3,2 zł = ............ zł ............ gr
e) 101,9 zł = ............ zł ............ gr
f) 12,03 zł = ............ zł ............ gr
Zapisz podane masy, używając liczb dziesiętnych.
a) 12 kg 20 dag = ............ kg wskazówka: 1 kg = 100 dag
b) 3 kg 27 g = ............ kg wskazówka: 1 kg = 1000 g
c) 7 dag 2 g = ............ dag wskazówka: 1 dag = 10 g
d) 1 t 240 kg = ............ t wskazówka: 1 t = 1000 kg
e) 20 t 81 kg = ............ t wskazówka: 1 t = 1000 kg
f) 8 t 3 kg = ............ t wskazówka: 1 t = 1000 kg
Zapisz podane masy, używając liczb dwumianowanych.
a) 3,019 kg = ............ kg ............ g
b) 18,28 kg = ............ kg ............ g
c) 18,29 kg = ............ kg ............ dag
d) 23,2 kg = ............ kg ............ dag
e) 100, 9 kg = ............ kg ............ g
f) 12,23 t = ............ t ............ kg
Zapisz podane długości, używając liczb dziesiętnych.
a) 12 km 278m = ............ km wskazówka: 1 km = 1000 m
b) 3 km 20 m = ............ km wskazówka: 1 km = 1000 m
c) 7 dm 2 cm = ............ dm wskazówka: 1 dm = 10 cm
d) 1 cm 2 mm = ............ cm wskazówka: 1 cm = 10 mm
e) 2 dm 1 mm = ............ dm wskazówka: 1 dm = 100 mm
f) 8 m 3 mm = ............ m wskazówka: 1 m = 1000 mm
Zapisz podane długości, używając liczb dwumianowanych.
a) 5,049 km = ............ km ............ m
b) 18,28 km = ............ km ............ m
c) 48,2 dm = ............ dm ............ cm
d) 93,41 dm = ............ dm ............ mm
e) 100,009 km = ............ km ............ cm
f) 102,07 m = ............ m ............ mm