Zaznaczanie na osi liczbowej zbiorów liczbowych
Oś liczbową definiuje się zazwyczaj jako obiekt geometryczny będący prostą z wyróżnionymi punktami. Żyjący w latach – niemiecki matematyk Georg Cantor zauważył, że każdemu punktowi na osi liczbowej odpowiada pewna liczba rzeczywista. Wśród liczb rzeczywistych są też liczby całkowite. Każda liczba całkowita jest liczbą rzeczywistą, ale nie każda liczba rzeczywista jest liczbą całkowitą. Wysnuł więc wniosek, że liczb rzeczywistych jest więcej niż całkowitych. To było odkrycie Cantora, a naszym zadaniem będzie zrozumienie, jak użyć osi liczbowej do zaznaczania na niej zbiorów liczbowych, spełniających określone warunki.
Interaktywna treść merytorycznaInteraktywna treść merytoryczna
AnimacjaAnimacja
Zestaw ćwiczeń interaktywnychZestaw ćwiczeń interaktywnych
SłownikSłownik
Pojęcie osi liczbowej.
Definicję liczby naturalnej, liczby całkowitej i liczby wymiernej.
Zaznaczysz na osi liczbowej zbiór liczb spełniających określone warunki.
Wyznaczysz na osi liczbowej liczby, które spełniają określone warunki.
Wykorzystasz zdobytą wiedzę do rozwiązywania problemów matematycznych.
Przypomnijmy definicję osi liczbowejosi liczbowej.
Osią liczbową nazywamy prostą, na której zaznaczamy: zwrot (strzałkę, która wskazuje, w którą stronę liczby się zwiększają), liczby oraz .
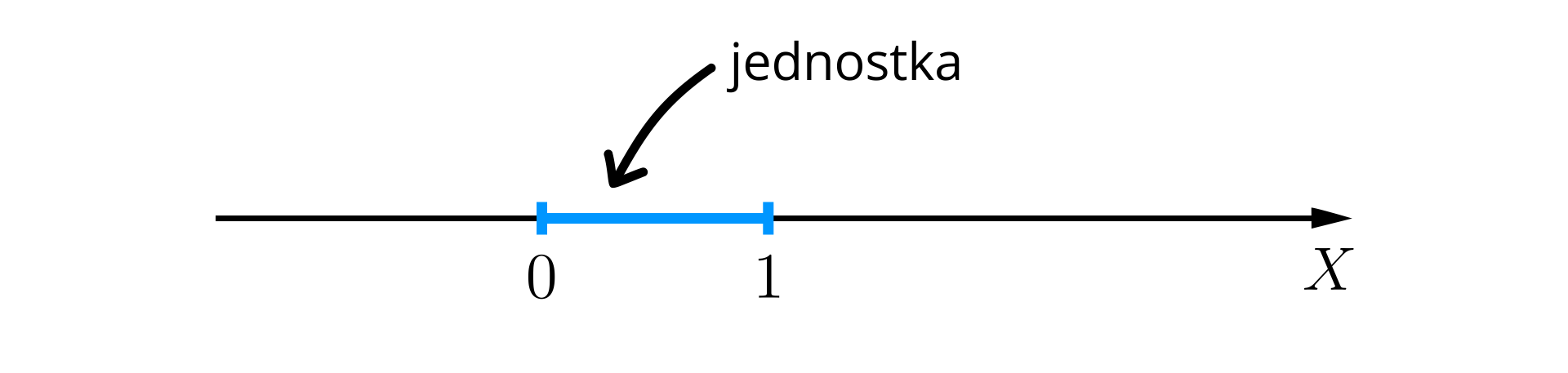
Punkty i wyznaczają końce odcinka, który nazywamy jednostką osi liczbowej, a jego długość jest równa .
Na osi liczbowej możemy zaznaczać nie tylko pojedyncze liczby, ale też zbiory liczb, spełniających określone warunki.
W zależności od warunku, jaki spełniają liczby na osi liczbowej, możemy wyróżnić kilka różnych przypadków.
Zaznaczymy na osi liczbowej zbiór liczb spełniających warunek:
Zapis oznacza, że jest liczbą większą od . Zatem na osi liczbowej mamy zaznaczyć wszystkie liczby, które są większe od liczby . Rysujemy oś liczbową i zaznaczamy na niej liczbę .
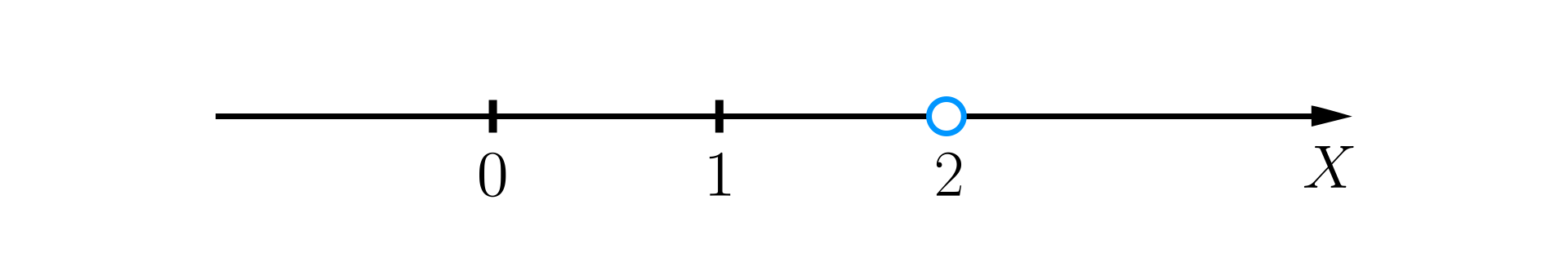
Liczby większe od leżą na osi liczbowej na prawo od tej liczby.

Pusta kropka przy liczbie oznacza, że ta liczba nie należy do omawianego zbioru liczb.
Zapis oznacza, że jest liczbą większą lub równą . Zatem na osi liczbowej mamy zaznaczyć liczby, które są większe lub równe liczbie . Rysujemy oś liczbową i zaznaczamy na niej liczbę .
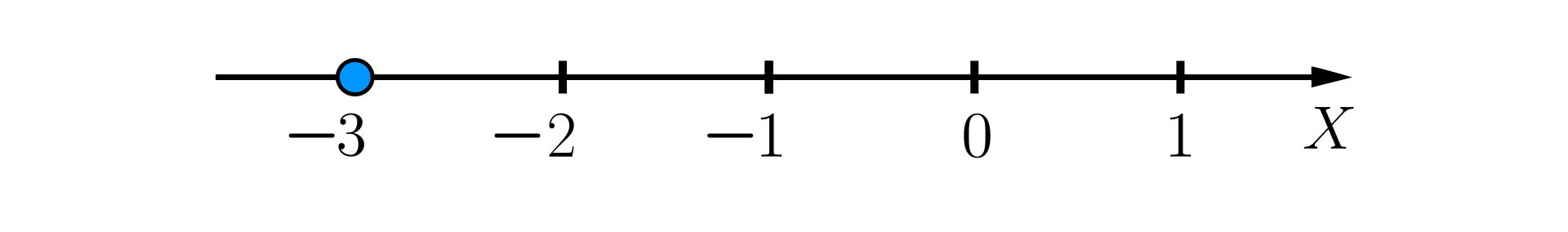
Liczby większe od leżą na osi liczbowej na prawo od tej liczby.

Zamalowana kropka przy liczbie oznacza, że ta liczba należy do omawianego zbioru liczb.
Zapis oznacza, że jest liczbą mniejszą od . Zatem na osi liczbowej mamy zaznaczyć liczby, które są mniejsze od liczby . Rysujemy oś liczbową i zaznaczamy na niej liczbę .

Liczby mniejsze od leżą na osi liczbowej na lewo od tej liczby.

Pusta kropka przy liczbie oznacza, że ta liczba nie należy do omawianego zbioru.
Zapis oznacza, że jest liczbą mniejszą lub równą . Zatem na osi liczbowej mamy zaznaczyć liczby, które są mniejsze lub równe liczbie . Rysujemy oś liczbową i zaznaczamy na niej liczbę .
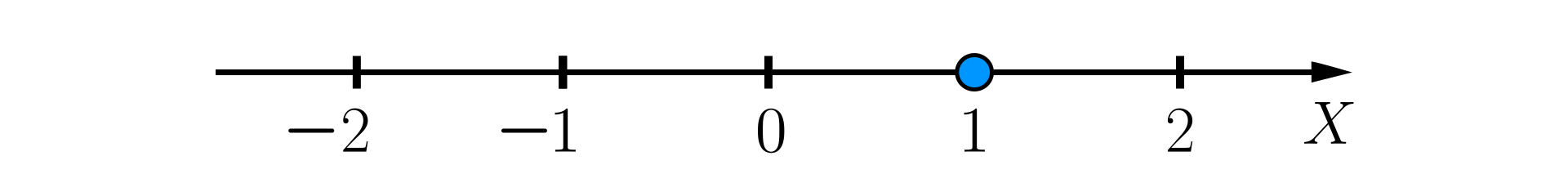
Liczby mniejsze od leżą na osi liczbowej na lewo od tej liczby.

Zamalowana kropka przy liczbie oznacza, że ta liczba należy do omawianego zbioru.
Zaznaczymy na osi liczbowej zbiór liczb spełniających warunek , a następnie podamy wszystkie liczby naturalne, które spełniają podany warunek.
Rozwiązanie:
Zapis oznacza, że jest liczbą mniejszą lub równą . Zatem na osi liczbowej mamy zaznaczyć liczby, które są mniejsze lub równe liczbie . Rysujemy oś liczbową i zaznaczamy na niej liczbę , a następnie liczby mniejsze od , które leżą na osi liczbowej na lewo od tej liczby.

Zatem liczby naturalne, które spełniają podany warunek to: , , , , .
Zapiszemy warunek, jaki spełniają liczby zaznaczone na osi liczbowej:


Rozwiązanie:
Zbiór liczb zaznaczony na osi liczbowej jest opisany za pomocą warunku .
Zbiór liczb zaznaczony na osi liczbowej jest opisany za pomocą warunku .
Zaznaczymy na osi liczbowej wszystkie liczby:
nie mniejsze niż ,
ujemne.
Rozwiązanie:
Liczby, które są nie mniejsze niż , to takie liczby , które spełniają warunek .
Wobec tego, zbiór liczb spełniających warunek przedstawia się na osi liczbowej następująco:

Liczby, które są ujemne, to takie liczby , które spełniają warunek .
Wobec tego, zbiór liczb spełniających warunek przedstawia się na osi liczbowej następująco:

Zaznaczymy na osi liczbowej wszystkie liczby, które spełniają jednocześnie podane warunki, a następnie wymienimy liczby całkowite, które spełniają te warunki.
wszystkie liczby mniejsze od i większe od ,
wszystkie liczby nie mniejsze niż i nie większe niż .
Rozwiązanie:
Liczby, które są mniejsze od i większe od , to takie liczby , które spełniają warunki: oraz .
Zatem:
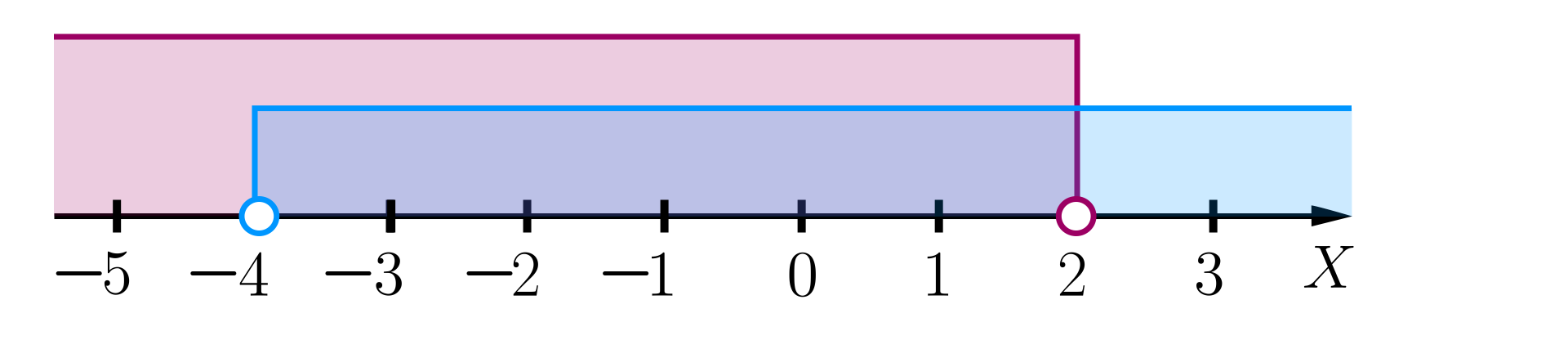
Liczby całkowite, które spełniają podane warunki to: .
Liczby, które są nie mniejsze niż i nie większe niż , to takie liczby , które spełniają warunki oraz .
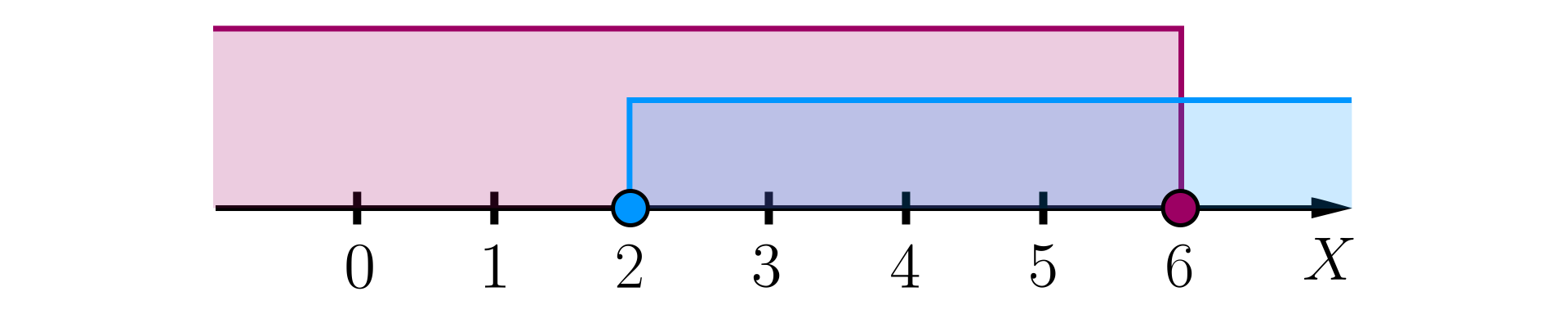
Liczby całkowite, które spełniają podane warunki to: .
Mając dane punkty na osi liczbowej, które odpowiadają wartościom liczb, możemy obliczać odległości pomiędzy tymi punktami.
Wyznaczymy zbiór liczb całkowitych, których odległość na osi liczbowej od liczby jest nie większa niż .
Rozwiązanie:
Narysujmy oś liczbową i zaznaczmy na niej liczbę .
Zauważmy, że liczby , których odległość od liczby jest nie większa niż spełniają warunki: oraz .
Omawiany zbiór liczb przedstawia się następująco na osi liczbowej:
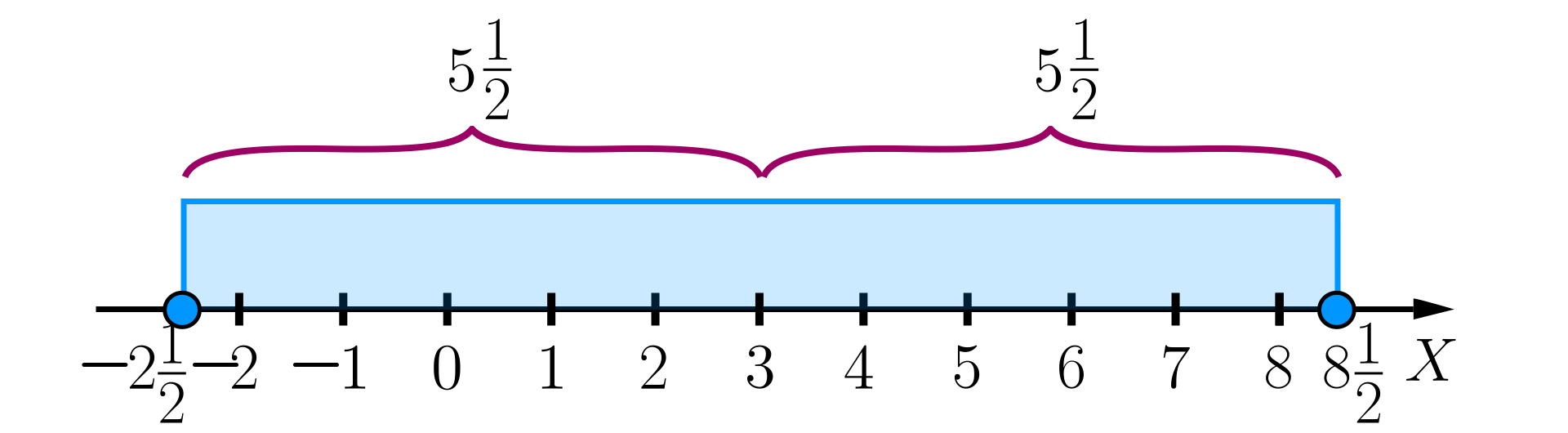
Liczby całkowite, które spełniają podany warunek to: , , , , , , , , , , .
Załóżmy, że pewien zbiór liczb jest określony za pomocą warunków oraz , gdzie jest pewną liczbą całkowitą. Wyznaczymy, ile liczb całkowitych należy do zbioru liczb, który jest określony za pomocą tych warunków jednocześnie.
Rozwiązanie:
Zauważmy, że jeśli jest pewną liczbą całkowitą, to .
Najmniejszą liczbą całkowitą, która należy do podanego zbioru jest , a największą .
Pomiędzy tymi liczbami znajdują się jeszcze liczby całkowite: , , .
Zatem jest liczb całkowitych, które spełniają oba warunki jednocześnie.
Notatnik
Animacja
Zapoznaj się z animacją dotyczącą zaznaczania na osi liczb spełniających podane warunki, a następnie wykonaj polecenia.

Film dostępny pod adresem /preview/resource/R1SDAkLG425O9
Film nawiązujący do treści materiału
Zapisz warunek, jaki spełniają liczby zaznaczone na osi liczbowej, a następnie określ najmniejszą i największą liczbę całkowitą należącą do tego zbioru.




Zestaw ćwiczeń interaktywnych
Na osi liczbowej zaznaczono warunek . Ile liczb naturalnych go spełnia? 1. , 2. , 3. , 4. zamalowanym, 5. , 6. niezamalowanym.
Na osi liczbowej zaznaczono warunek . Oznacza to, ze liczbę oznaczono 1. , 2. , 3. , 4. zamalowanym, 5. , 6. niezamalowanym kółeczkiem na osi liczbowej.
Do zbioru liczb określonego za pomocą warunku należy 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. liczb naturalnych.
Do zbioru liczb określonego jednocześnie za pomocą warunków oraz należą 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. liczby naturalne.
Zaznacz na osi liczbowej zbiór wszystkich liczb, które spełniają jednocześnie warunki: oraz , a następnie podaj:
wszystkie liczby naturalne, które spełniają jednocześnie podane warunki,
wszystkie liczby całkowite, które spełniają jednocześnie podane warunki.
Na osi liczbowej przedstawiono liczby opisane za pomocą pewnego warunku.

Podaj:
liczby przeciwne do wszystkich liczb naturalnych, które należą do tego zbioru,
liczby odwrotne do pięciu największych liczb całkowitych ujemnych, które należą do tego zbioru.
Słownik
przedstawienie zbioru liczb w postaci prostej z wyróżnionymi punktami i oraz o określonym zwrocie
Bibliografia
Cewe A., Nahorska H., Krawczyk M., Magryś‑Walczak A., (2017), Matematyka. Zamiast korepetycji z matematyki. Zbiór zadań otwartych i zamkniętych z matematyki dla klas i , Gdańsk: Wydawnictwo Podkowa.
Duvnjak E., Kokiernak‑Jurkiewicz E., (2018), Matematyka . Zbiór zadań. Szkoła podstawowa, Warszawa:Wydawnictwa Szkolne i Pedagogiczne.
Janowicz J., (2018), Matematyka. Zbiór zadań konkursowych dla klas szkoły podstawowej, Gdańsk: Gdańskie Wydawnictwo Oświatowe.
