Budujemy wieżę Hanoi
Tematyka tego materiału wykracza ponad podstawę programową do informatyki w szkole podstawowej. Realizujemy w nim zagadnienia, z którymi bliżej zapoznasz się na lekcjach informatyki w szkole ponadpodstawowej.
W świecie zagadek matematycznych istnieje jedna, która wyróżnia się spośród innych swoją prostotą i jednocześnie trudnością. Mowa o Zagadce Wież Hanoi. Ta łamigłówka sprawia, że nawet najbardziej doświadczone umysły muszą skoncentrować się na znalezieniu poprawnego rozwiązania. Historia i zasady tej zagadki sięgają daleko w przeszłość i wciąż przyciągają entuzjastów, badaczy i poszukiwaczy wyzwań.
Historia zagadki Wież Hanoi

Zagadka Wież Hanoi została opracowana po raz pierwszy przez francuskiego matematyka Françoisa Édouarda Anatola Lucasa w roku. Zagadkę zaprezentowano wraz z tybetańską legendą o świątyni Brahmy w Indiach, jednak chcąc zdobyć większą popularność, w jej nazwie nawiązano do Wietnamu, o którym ówcześnie dużo mówiło się we Francji. Na przestrzeni wieków powstało wiele wersji tej historii, w tym właśnie o wieżach w Hanoi, stolicy Wietnamu. Zgodnie z nią w świątyni znajdowały się trzy wieże. Według legendy na pierwszej z nich znajdować się miały 64 krążki o różnych średnicach ułożone na stosie.
Krążki były ułożone tak, że krążek o największej średnicy znajdował się na samym dole, a kolejne krążki były ułożone zgodnie ze średnicami (od największej do najmniejszej).
Mnisi mieszkający w świątyni mieli za zadanie przełożyć krążki na inną wieżę, przestrzegając równocześnie pewnych ustalonych zasad. Mówi się, że gdyby udało im się zakończyć to zadanie, nastąpiłby koniec świata. Zakładając, że przełożenie jednego krążka zajmuje jedną sekundę, rozwiązanie zagadki trwałoby 600 miliardów lat.
Indeks górny Moscovich I., 1000 playthinks: puzzles, paradoxes, illusions & games, Workman, 2001. Indeks górny koniecMoscovich I., 1000 playthinks: puzzles, paradoxes, illusions & games, Workman, 2001.
Indeks górny Andreas M. Hinz, Sandi Klavžar, Uroš Milutinović, Ciril Petr, The Tower of Hanoi – Myths and Maths, 2013 Indeks górny koniecAndreas M. Hinz, Sandi Klavžar, Uroš Milutinović, Ciril Petr, The Tower of Hanoi – Myths and Maths, 2013
Zasady rozwiązywania łamigłówki Wież Hanoi
Dane są trzy słupki oraz zestaw krążków o różnych średnicach. Na początku wszystkie krążki są ułożone w stos na jednym słupku w kolejności malejącej, od największego na dole do najmniejszego na górze.
Zasady rozwiązywania zagadki są bardzo proste.
Wykonując ruch, można przenieść tylko jeden krążek.
Krążek można umieścić tylko na słupku, który jest pusty, albo znajduje się na nim większy od przenoszonego krążek.
W trakcie przenoszenia krążka nie wolno położyć go na krążku mniejszym.
Zagadka zostaje rozwiązana w momencie, gdy wszystkie krążki zostaną przeniesione ze słupka pierwszego na ostatni.
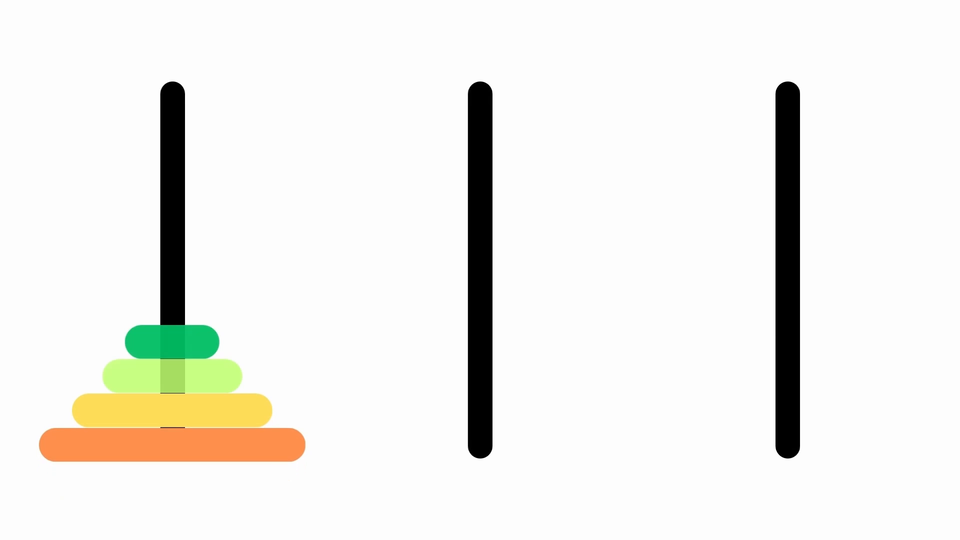
Film dostępny pod adresem /preview/resource/RGBk9RIXolmkr
Film przedstawiający zasadę rozwiązywania wież Hanoi.
Sposoby rozwiązywanie zagadki Wież Hanoi
Zasady rozwiązywania zagadki nie są skomplikowane, ale rozwiązanie nie jest już takie oczywiste. Istnieje wzór, który w prosty sposób opisuje minimalną liczbę kroków, które należy wykonać, aby ułożyć Wieżę Hanoi:
gdzie n oznacza liczbę krążków.
Oto minimalna liczba kroków do wykonania w zależności od liczby krążków:
1 krążek:
2 krążki:
3 krążki:
4 krążki:
5 krążków:
6 krążków:
Zagadka jest możliwa do rozwiązania przy wykonaniu większej liczby ruchów, jednak zakładając, że wykonanie jednego ruchu zajmuje jedną sekundę, to już przy sześciu krążkach zagadkę rozwiązywać będziemy przynajmniej ponad minutę.
Okazuje się, że zagadkę rozwiązać możemy, powtarzając trzy ruchy. Co więcej, trzymając się tych zasad, rozwiążemy ją, wykorzystując najmniejszą możliwą liczbę ruchów.
Zaprezentujmy ruchy, które należy wykonać. W tym celu oznaczymy kolejne słupki. Słupek początkowy nazwiemy „A”, słupek pomocniczy nazwiemy „B”, a docelowy „C”.
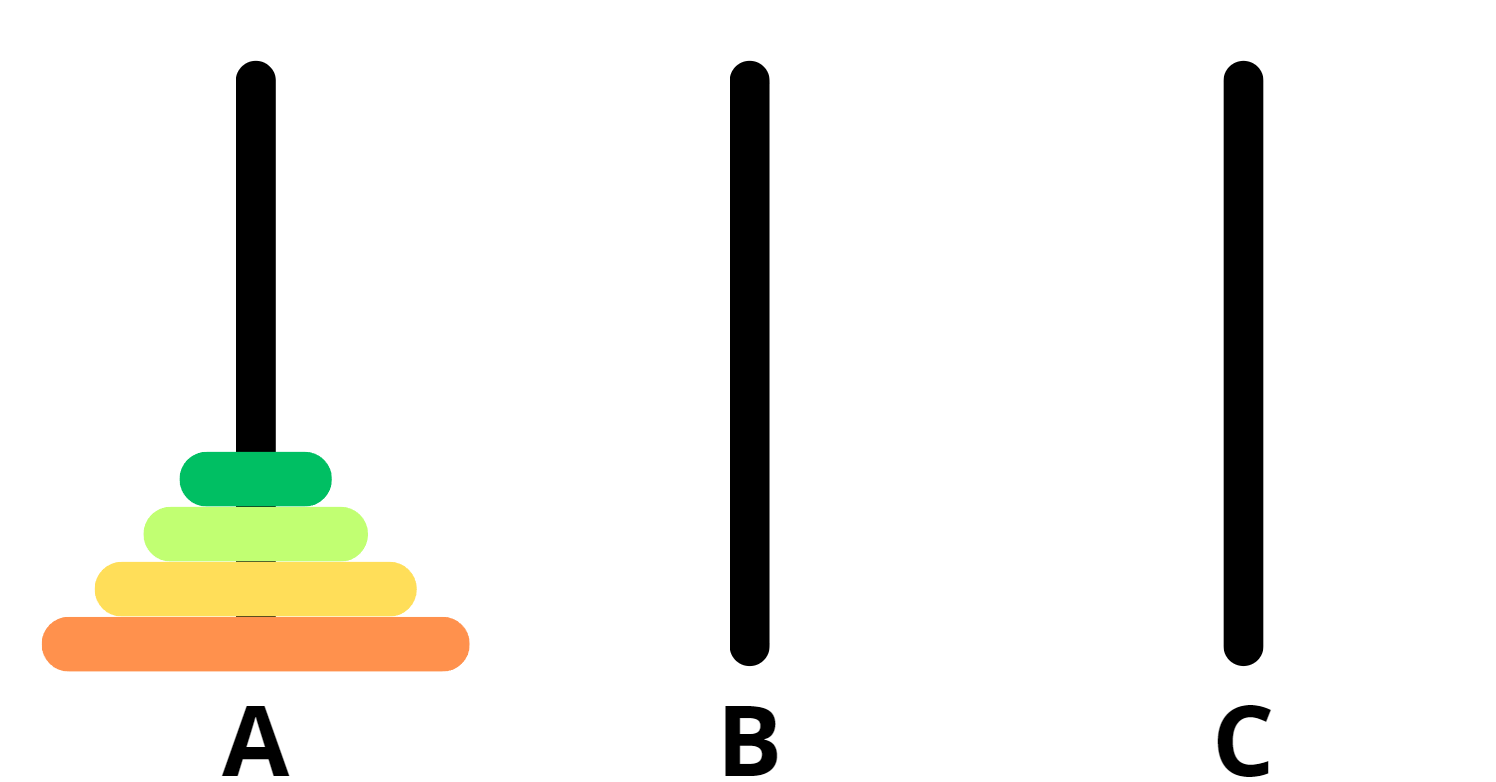
Jeśli przy takim przypisaniu słupków zaczniemy wykonywać ruchy między słupkami A i B, A i C oraz B i C w przypadku parzystej liczby krążków albo A i C, A i B oraz B i C w przypadku nieparzystej liczby krążków, to uda nam się ułożyć wieżę w najmniejszej liczbie kroków.
Zasada ta została zaprezentowana poniżej:
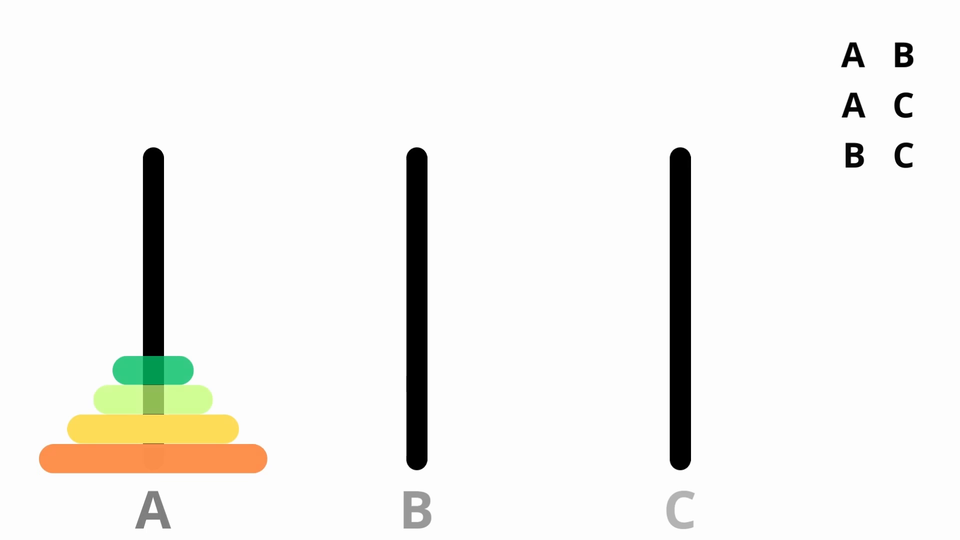
Film dostępny pod adresem /preview/resource/RPOlp2PlGLOrz
Film przedstawiający rozwiązywanie zagadki Wież Hanoi w minimalnej liczbie kroków.
To nie jedyny sposób. Wieżę Hanoi możemy ułożyć, wykorzystując metodę binarną. Jeśli wypiszemy kolejne liczby systemu binarnego, będziemy mogli rozwiązać zagadkę (również wykorzystując minimalną liczbę kroków).
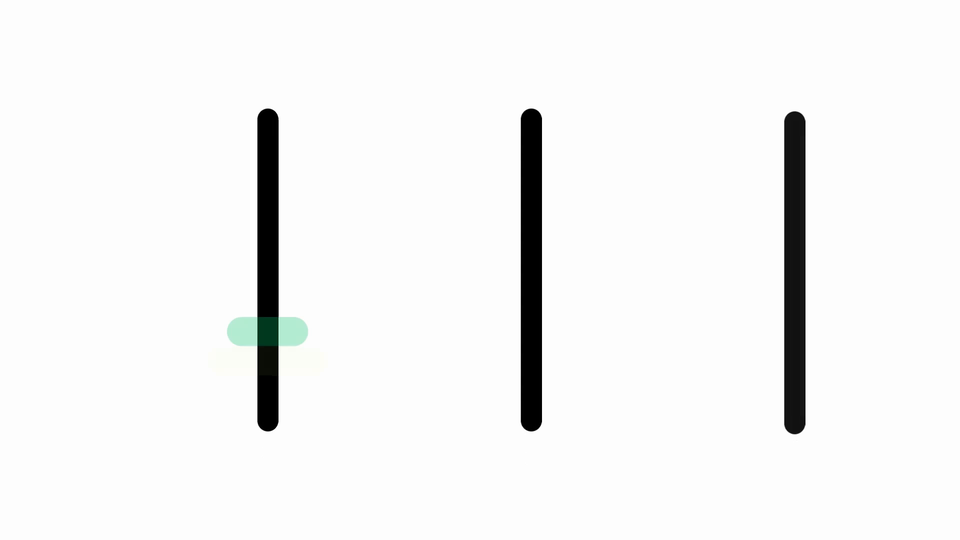
Film dostępny pod adresem /preview/resource/R1SfwGHPmUUbW
Film przedstawiający rozwiązywanie zagadki Wież Hanoi za pomocą metody binarnej.
Zagadka Wież Hanoi ma kilka różnych wariantów. W jednym z nich stosujemy się do wszystkich opisanych wcześniej zasad, ale dodajemy kolejny wymóg – konieczne jest przejście przez wszystkie unikalne kombinacje ustawień krążków. Dodatkowo żadna z kombinacji nie może się powtórzyć.
Liczbę unikalnych ustawień krążków możemy obliczyć ze wzoru:
gdzie n oznacza liczbę krążków.
Dodatkowo, odejmując od tej liczby jeden, otrzymamy liczbę kroków, którą należy wykonać, aby przygotować wszystkie kombinacje ustawień krążków. Tak więc wzór na minimalną liczbę kroków prezentuje się następująco:
gdzie n oznacza liczbę krążków.
Aby stworzyć te wszystkie ułożenia, zastosujemy się do metody trójkowejtrójkowej. Metoda ta jest bardzo podobna do metody binarnej, jednak wykorzystuje system trójkowy (jego podstawą jest liczba trzy). Warto zaznaczyć, że tym sposobem wykonamy więcej przesunięć krążków niż przy wykorzystaniu systemu binarnego.
Film dostępny pod adresem /preview/resource/RMcFeidCXh5km
Film przedstawiający rozwiązywanie zagadki Wież Hanoi z tworzeniem wszystkich możliwych kombinacji za pomocą metody trójkowej.
Możliwe ustawienia krążków możemy przedstawić na grafie. Rozpoczynamy rysowanie grafu od stanu, w którym wszystkie krążki znajdują się na pierwszym słupku. Następnie rozpisujemy możliwości ułożenia krążków, wykonując jeden ruch. Rozpisujemy na grafie wszystkie możliwe ułożenia krążków. Graf układa się w kształt trójkąta, gdzie lewy dolny narożnik zawiera takie ustawienie krążków, że wszystkie znajdują się na stosie środkowym, a prawy narożnik zawiera ustawienie, w którym wszystkie krążki znajdują się na stosie ostatnim. Tak prezentuje się graf dla trzech krążków:
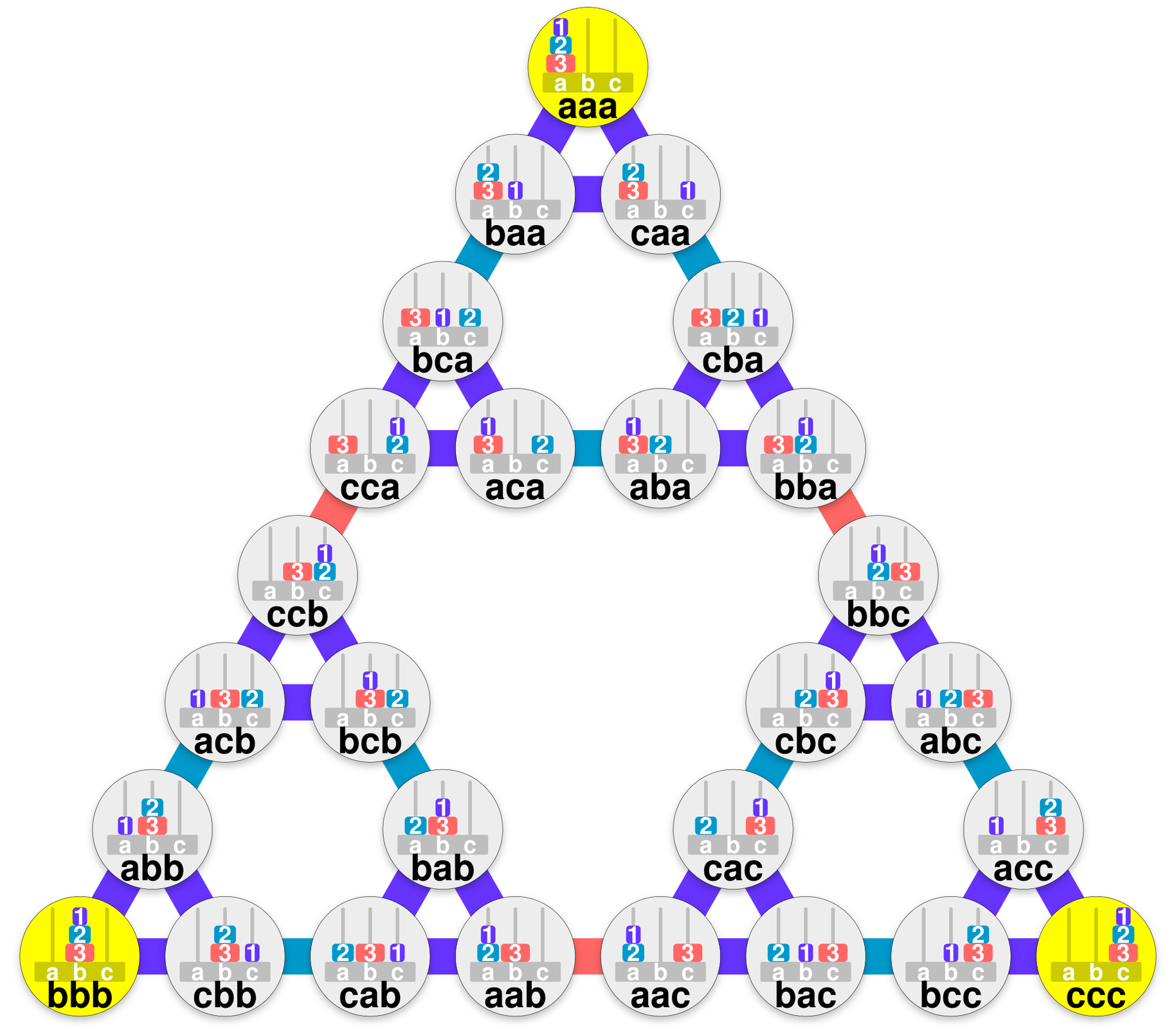
Zwróć uwagę na oznaczenia aaa, abb itd. Składają się one z trzech liter, pierwsza odpowiada pierwszemu krążkowi, druga odpowiada drugiemu krążkowi, trzecia odpowiada trzeciemu krążkowi. Litera a odpowiada pierwszemu stosowi, litera b odpowiada drugiemu stosowi, a litera c odpowiada trzeciemu stosowi. Zatem oznaczenie acc oznacza, że pierwszy krążek znajduje się na stosie a, a krążki drugi i trzeci na stosie c.
Tak prezentuje się graf, gdy w zagadce wykorzystujemy siedem krążków:

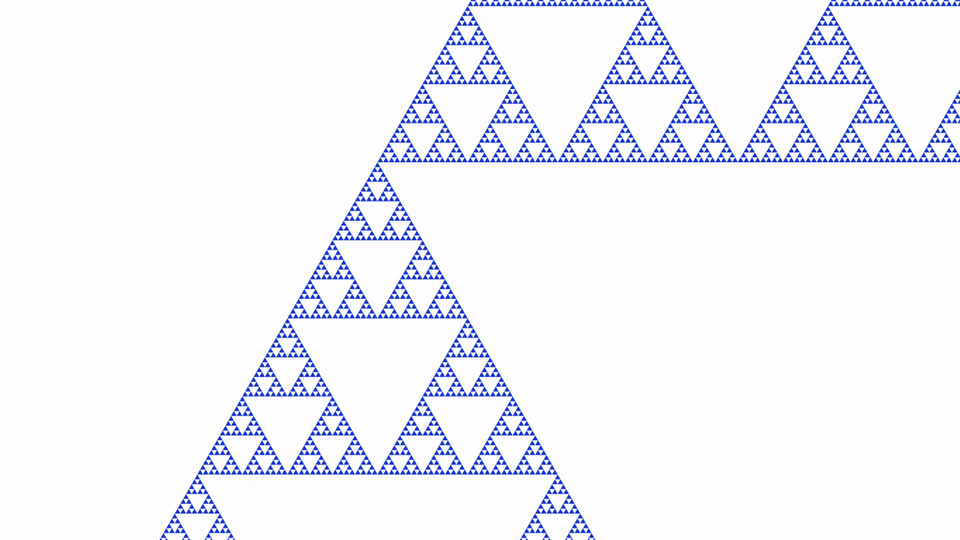
Graf ten jest przybliżeniem trójkąta Sierpińskiegotrójkąta Sierpińskiego, który jest fraktalemfraktalem.
W animacji przedstawiono trójkąt Sierpińskiego. Zwróć uwagę na strukturę fraktalu na różnych poziomach przybliżenia. Wykazuje ona samopodobieństwosamopodobieństwo i powtarza się rekurencyjnierekurencyjnie.
Film dostępny pod adresem /preview/resource/RY6WzgtanlphE
Film przedstawiający fraktal czyli trójkąt Sierpińskiego.
Pseudokod
Omówiliśmy sposoby zapisu algorytmów takie jak lista kroków czy schemat blokowy. Oprócz nich istnieje jeszcze sposób zapisu zwany pseudokodem.
Pseudokod to mieszanka języka naturalnego i elementów programowania. Jest bardziej formalny niż lista kroków, ale pomimo zachowania charakterystycznej struktury jest mniej szczegółowy niż kod w języku programowania.
W dalszej części posługujemy się nieco innymi oznaczeniami. Stos A to stos źródłowy, stos B to stos pomocniczy, a stos C to stos docelowy.
Zagadkę Wież Hanoi możemy oczywiście rozwiązać za pomocą programu komputerowego. W tym celu możemy wybrać jedną z dwóch technik – iteracyjnąiteracyjną lub rekurencyjnąrekurencyjną.
Z rekurencją zapoznasz się bliżej na lekcjach informatyki w szkole średniej.
Tak prezentuje się pseudokod przedstawiający rozwiązanie zagadki Wież Hanoi metodą iteracyjną:
W pseudokodzie wykorzystujemy operator mod. To operator modulo, czyli obliczania reszty z dzielenia.
W pseudokodzie rozwiązanie jest przedstawione przy użyciu pętli i instrukcji warunkowej. Algorytm zaczyna od ustalenia trzech stosów: źródłowego, pomocniczego i docelowego. Następnie sprawdza, czy liczba krążków jest parzysta, ponieważ zależy od tego, które stosy będą pełnić rolę pomocniczą i docelową. Jeśli liczba krążków jest parzysta, stosPomocniczy i stosDocelowy zostają zamienione miejscami.
Następnie algorytm wykonuje w pętli przesunięcia (ruchy) krążków. W każdej iteracji sprawdzane jest, który ruch należy wykonać na podstawie wartości reszty z dzielenia i przez 3. Jeśli reszta z dzielenia wynosi 1, to przenosimy krążek ze stosuŹródłowego na stosDocelowy. Jeśli wynosi 2, przenosimy krążek ze stosuŹródłowego na stosPomocniczy. Jeśli wynosi 0, przenosimy krążek ze stosuPomocniczego na stosDocelowy.
Tak prezentuje się pseudokod przedstawiający rozwiązanie zagadki Wież Hanoi metodą rekurencyjną:
Rozwiązanie jest przedstawione przy użyciu rekurencji, czyli wywoływania tej samej funkcji dla mniejszych podproblemów. Algorytm sprawdza, czy liczba krążków jest równa 1. Jeśli tak, wykonuje ruch przeniesienia krążka ze stosuŹródłowego na stosDocelowy. Jeśli jednak liczba krążków jest większa niż 1, algorytm rekurencyjnie wykonuje trzy kroki:
Wywołuje się dla mniejszego podproblemu, przekazując wartości
liczbaKrążków - 1,stosŹródłowyjako stos źródłowy,stosDocelowyjako stos pomocniczy istosPomocniczyjako stos docelowy.Wykonuje ruch przeniesienia krążka ze
stosuŹródłowegonastosDocelowy.Wywołuje się dla mniejszego podproblemu, przekazując
liczbaKrążków‑1,stosPomocniczyjako stos źródłowy,stosŹródłowyjako stos pomocniczy istosDocelowyjako stos docelowy.
Te kroki powtarzamy aż do sytuacji, w której liczba krążków do przeniesienia będzie równa 1. Wykonany zostanie w ten sposób ostatni ruch przeniesienia krążka.
Notatnik
Symulacja
Zestaw ćwiczeń interaktywnych
n oznacza liczbę krążków w zagadce Wież Hanoi. Wskaż wzór, za pomocą którego można obliczyć minimalną liczbę kroków, które należy wykonać, aby rozwiązać zagadkę.Zapoznaj się z pseudokodem.
Brakuje w nim pewnych fragmentów: XXX, YYY, ZZZ, QQQ, WWW.
XXX w pseudokodzie.YYY w pseudokodzie.ZZZ w pseudokodzie.QQQ w pseudokodzie.WWW w pseudokodzie.Słownik
powtarzający się proces lub pętla, w którym pewna czynność jest wykonywana wielokrotnie w celu osiągnięcia określonego rezultatu. Powtarzanie może obejmować wykonywanie tych samych instrukcji wielokrotnie na podstawie pewnego warunku lub przechodzenie przez elementy w zbiorze danych jeden po drugim
technika programistyczna, w której funkcja lub procedura wywołuje samą siebie. Umożliwia to rozwiązanie problemów, które można podzielić na mniejsze podproblemy tego samego rodzaju
pozycyjny, dwójkowy system liczbowy, którego podstawą jest liczba 2, a do zapisu wykorzystuje się dwie cyfry – 0 i 1; w tym systemie liczby reprezentowane są przez kombinacje tych cyfr, np. liczba 101 w systemie binarnym oznacza, że mamy 1 czwórkę, 0 dwójek i 1 jednostkę, a więc 101Indeks dolny (2)(2) = 5Indeks dolny (10)(10); w systemie binarnym każda pozycja liczby ma wagę równą kolejnym potęgom liczby 2, zaczynając od potęgi 2Indeks górny 00 dla bitu o najniższej wartości (najmniej znaczący bit znajdujący się po prawej stronie); system binarny jest wykorzystywany w informatyce i elektronice cyfrowej, ponieważ można go łatwo reprezentować za pomocą dwóch stanów, takich jak prawda/fałsz albo włączone/wyłączone
pozycyjny system liczbowy; składa się z dziesięciu cyfr: 0, 1, 2, 3, 4, 5, 6, 7, 8 i 9; każda liczba w tym systemie jest tworzona przez kombinację tych cyfr, np. liczba 227 w systemie dziesiętnym oznacza, że mamy 2 setki, 2 dziesiątki i 7 jedności; w systemie dziesiętnym każda pozycja liczby ma wagę równą kolejnym potęgom liczby 10, zaczynając od potęgi 10Indeks górny 00 dla najmniej znaczącej cyfry (jedności).
pozycyjny system liczbowy, w którym liczby reprezentowane są przez trzy cyfry: 0, 1 i 2; każda liczba jest tworzona przez kombinację tych cyfr, np. liczba 201 w systemie trójkowym oznacza, że mamy 2 dziewiątki, 0 trójek i 1 jednostkę, a więc 201Indeks dolny (3)(3) = 19Indeks dolny (10)(10); w systemie trójkowym każda pozycja liczby ma wagę równą kolejnym potęgom liczby 3, zaczynając od potęgi 3Indeks górny 00 dla najmniej znaczącej cyfry; system trójkowy nie jest tak powszechny, jak system dziesiętny, ale jest używany w niektórych naukach, takich jak teoria liczb czy informatyka
właściwość figur, która polega na tym, że jej części są podobne do całości
(łac. fractus – złamany, cząstkowy, ułamkowy) obiekt samopodobny, czyli taki, którego części są podobne do całości, oznacza to, że część fraktala wygląda podobnie do całego obiektu, niezależnie od powiększenia; fraktale często mają złożone i nieregularne kształty, które powtarzają się w coraz mniejszych szczegółach; są one stosowane w matematyce, naukach przyrodniczych, grafice komputerowej i sztuce
jeden z najbardziej znanych fraktali; tworzony poprzez podział równobocznego trójkąta na cztery mniejsze równoboczne trójkąty, a następnie powtarzanie tych kroków dla każdego z tych trójkątów; tworzą się w ten sposób coraz mniejsze kopie trójkąta początkowego