7. Kołyska Newtona
Kołyska NewtonaKołyska Newtona służy ilustracji zasady zachowania energii i pędu podczas sprężystego zderzenia kul. Składa się z kilku jednakowych wahadeł, utworzonych ze stalowych kul zawieszonych na niciach, które mogą wykonywać wahania tylko w jednej płaszczyźnie pionowej.
Dla wprawienia kołyski w ruch, wahadła powinny być wychylane i zwalniane w sposób zapewniający centralne zderzenia kul zachodzące na jednej prostej. Gdy jedna z kul zostanie odchylona i puszczona, jej uderzenie w pozostałe kule spowoduje, że po przeciwnej stronie szeregu odskoczy tylko ostatnia kula. Jej wychylenie będzie prawie takie samo jak pierwszej. Analogicznie, gdy odchyli się i puści dwie kule, z drugiego końca odskoczą również dwie kule. Ogólnie rzecz biorąc, tyle samo kul odskoczy na końcu szeregu, ile zostało odchylonych na jego początku, zaś pozostałe (środkowe) kule pozostaną nieruchome. Zachowanie to, bez znajomości praw fizyki, może być postrzegane jako coś zaskakującego.
poznasz podstawowe prawa odpowiedzialne za zachowanie się kul Newtona;
wymienisz siły działające na poszczególne kule podczas zderzeń;
zdefiniujesz zasady zachowania podczas zderzeń sprężystych kul;
określisz zasadę zachowania energii dla kul Newtona i uzupełnisz opis zasadą zachowania pędu;
przeanalizujesz zachowanie poszczególnych kul podczas odchyleń i wykonasz e‑doświadczenie z kulkami Newtona;
zaproponujesz wykorzystanie praw fizyki kul Newtona w innych podobnych zjawiskach.
Przeczytaj
Opis działania

Po raz pierwszy kołyska Newtona objaśniona i zademonstrowana została przez francuskiego fizyka Abbé Mariotte z Francuskiej Akademii Nauk w r. Choć nazwa przypisywana jest Newtonowi, należałoby nazywać ją „kołyską Mariotte'a” który, na podstawie doświadczeń ze zderzającymi się kulami, opisał i wyjaśnił zjawiska warunkujące jej działanie.
Działanie kołyski Newtona jest rezultatem serii wielu szybko po sobie następujących zderzeń. Za każdym razem kule stykają się, odkształcają sprężyście i odpychają. Seria zderzeń trwa ułamek milisekundy, więc nie jesteśmy w stanie ich rozróżnić. Zauważamy tylko końcowy efekt. Widać więc, że wystąpiłaby charakterystyczna dla wahadła Newtona symetria wychyleń.
Kluczowym procesem, który powtarza się tu wielokrotnie i decyduje o przebiegu zjawisk, jest wymiana prędkości możliwa dzięki zderzeniom centralnym kul o jednakowych masach.
Dla wyjaśnienia tych efektów trzeba uświadomić sobie ważną konsekwencję zasad zachowania energii i pędu: dwie kule o jednakowych masach, zderzające się centralnie, wymieniają się prędkościami (oczywiście jeśli straty energii podczas ruchu i przy zderzeniu są zaniedbywalne). W szczególnym przypadku, gdy jedna z kul spoczywa, po zderzeniu przejmuje prędkość drugiej, która zatrzymuje się. Zderzenia kul są prawie doskonale sprężyste, czyli zachowana jest przy nich energia kinetyczna zderzających się ciał. Z zasady zachowania energii i zasady zachowania pędu wynika – przy założeniu, że masy obu ciał są takie same, a pierwsze ciało się poruszało, natomiast drugie było nieruchome – że po zderzeniu pierwsze ciało się zatrzymuje, a drugie porusza z taką prędkością, jaką miało pierwsze ciało. W ten sposób pęd przekazywany jest w całości następnej kuli, która przekazuje go kolejnej. Dopiero ostatnia kula, nie mogąc przekazać pędu dalej, sama zaczyna się poruszać. Jeśli odchylone zostały dwie (trzy lub więcej) kule, ich pęd zostaje przekazany w całości ostatnim dwóm (trzem lub więcej) kulom. Przenoszenie pędu odbywa się bardzo szybko, niezauważalnie dla obserwatora. Dla stalowych kulek prędkość przekazu pędu równa jest prędkości podłużnej fali mechanicznej w stali, czyli około .
Zasada zachowania energii
Prawo zachowania energii mówi, że energii – zdolności do wykonywania pracy – nie można ani stworzyć, ani zniszczyć. Energia może jednak zmieniać formy, z czego korzysta kołyska Newtona – szczególnie z przekształcania energii potencjalnej w energię kinetyczną i odwrotnie. Energia potencjalna to energia, którą obiekty zmagazynowały dzięki grawitacji lub ich elastyczności, natomiast energia kinetyczna to energia, którą obiekty mają będąc w ruchu.
Ponumerujmy kule od pierwszej do piątej. Kiedy wszystkie pięć jest w spoczynku, każda ma zerową energię potencjalną, ponieważ nie może opuścić się niżej, i zero energii kinetycznej, ponieważ się nie porusza. Kiedy pierwsza kula jest podniesiona i wychylona, jej energia kinetyczna pozostaje zerowa, ale jej energia potencjalna jest większa, ponieważ grawitacja może spowodować jej spadek i ruch po łuku wymuszony przez nić. Po wypuszczeniu kuli, jej energia potencjalna jest przekształcana w energię kinetyczną podczas jej spadku z powodu działania grawitacji.
Kiedy kula osiągnęła najniższy punkt, jej energia potencjalna wynosi zero, a jej energia kinetyczna jest teraz największa. Ponieważ energii nie można zniszczyć, największa energia kinetyczna kuli jest równa jej największej energii potencjalnej. Kiedy kula pierwsza uderza kulę drugą, zatrzymuje się natychmiast, a jej energia kinetyczna i potencjalna wraca do zera, ponieważ przekazana zostaje do kuli drugiej.
Energia kuli pierwszej jest przekazywana do kuli drugiej jako energia potencjalna, gdy ulega ona odkształceniu pod wpływem siły uderzenia. Gdy kula druga powraca do swojego pierwotnego kształtu, ponownie przekształca swoją energię potencjalną w energię kinetyczną, przenosząc tę energię na kulę trzecią, powodując jej odkształcenie. Kula zasadniczo działa jak sprężyna.
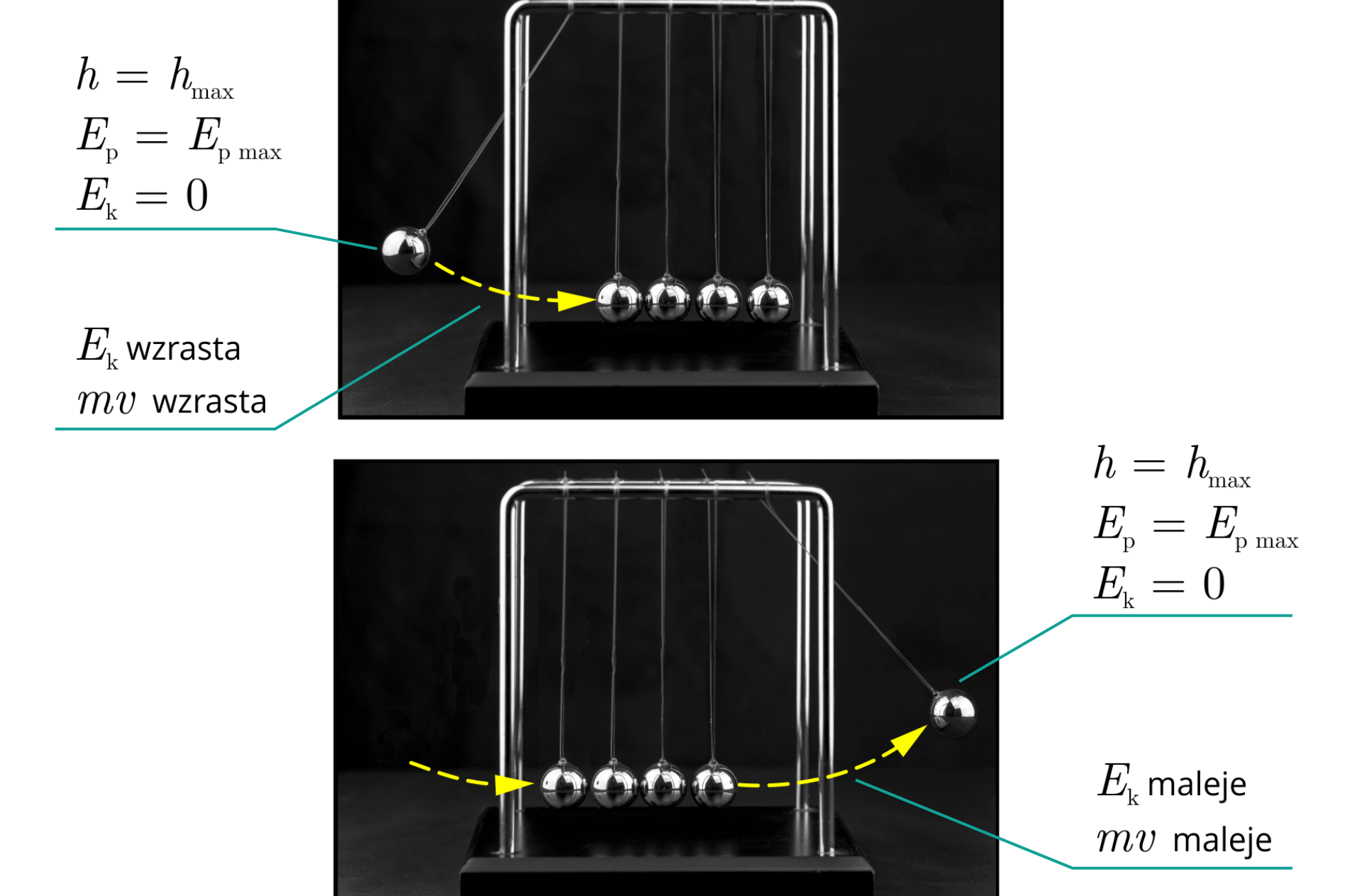
Ten transfer energii trwa dalej wzdłuż linii, aż dotrze do kuli ostatniej, która wyskakuje. Ze względu na zasadę zachowania energii, kula ta będzie miała taką samą ilość energii kinetycznej jak kula pierwsza, a więc będzie się wychylać z taką samą prędkością, jaką miała kula pierwsza w momencie uderzenia drugiej.
Jedna spadająca kula daje wystarczająco dużo energii, aby przemieścić drugą kulę na tę samą odległość, na którą spadła, z taką samą prędkością, z jaką spadła. Podobnie, dwie kule dają wystarczającą ilość energii, aby poruszyć dwie kule i tak dalej. Ale dlaczego kula po prostu nie odbije się tak, jak przyleciała? Dlaczego ruch jest kontynuowany tylko w jednym kierunku? W tym momencie w grę wchodzi zasada zachowania pędu.
Zasada zachowania pędu
Pęd jest wielkością fizyczną stosowaną do opisu ciał w ruchu. Można by rozumieć go jako coś w rodzaju „ilości” ruchu lub „siły” ruchu. Wszystko, co się porusza, ma pęd równy swojej masie pomnożonej przez swoją prędkość. Podobnie jak energia, pęd jest zachowany. Należy zauważyć, że pęd jest wielkością wektorową, co oznacza, że kierunek i zwrot pędu jest częścią jego definicji; nie wystarczy powiedzieć, że obiekt ma pęd, trzeba określić kierunek i zwrot pędu.
Kiedy kula pierwsza uderza kulę drugą, porusza się z prędkością w określonym kierunku (wzdłuż określonej prostej) i ma określony zwrot – powiedzmy, że z zachodu na wschód. Oznacza to, że pęd kuli ma również zwrot na wschód. Każda zmiana kierunku ruchu byłaby zmianą pędu, co nie może nastąpić bez wpływu siły zewnętrznej. Dlatego kula pierwsza nie odbija się po prostu od kuli drugiej – pęd przekazywany jest przez wszystkie kule w kierunku wschodnim.
Uwaga. Kula zatrzymuje się na krótko w górnej części łuku; jeśli pęd wymaga ruchu, jak jest zachowywany? Wygląda na to, że kołyska łamie zasadę zachowania pędu. Powodem, dla którego tak nie jest, jest to, że prawo zachowania działa tylko w układzie izolowanym, czyli takim, który jest wolny od jakiejkolwiek siły zewnętrznej – a kołyska Newtona nie jest układem izolowanym. Gdy kula piąta odskakuje od pozostałych kul, to również podskakuje. Kiedy to robi, jest pod wpływem siły grawitacji, która spowalnia kulę, oraz zmieniającej kierunek prędkości nici. Tak więc zasadę pędu stosujemy od momentu zaraz przed zderzeniem do momentu zaraz po zderzeniu.
Kule bilardowe
Dokładniejszą analogią układu izolowanego są kule bilardowe: w momencie uderzenia pierwsza kula zatrzymuje się, a druga kontynuuje ruch w linii prostej. W tym przykładzie grawitacja nie ma znaczenia, ponieważ działa prostopadle do ruchu kulek i jest równoważona przez znajdujący się pod kulami stół, a więc nie wpływa na ich prędkość ani kierunek ruchu. W praktyce układ izolowany jest niemożliwy, ponieważ grawitacja i tarcie zawsze występują w układach rzeczywistych.
Pozioma linia kul w spoczynku funkcjonuje jako układ zamknięty, wolny od wpływu jakiejkolwiek siły innej niż grawitacja. To tutaj, w krótkim czasie między uderzeniem pierwszej kuli a wychyleniem się kuli końcowej, pęd jest zachowany.
Kiedy kula osiąga swój szczyt, wraca do posiadania jedynie energii potencjalnej, a jej energia kinetyczna i pęd zostają zredukowane do zera. Grawitacja zaczyna wtedy przyciągać kulę w dół, ponownie rozpoczynając cykl.
Kołyska Newtona matematycznie
Kołyskę Newtona można dość dokładnie opisać za pomocą prostych równań matematycznych przy założeniu, że kulki zawsze zderzają się parami.
Zasada zachowania pędu () i wzór ne energię kinetyczną () mogą być wykorzystane do wyznaczenia prędkości wypadkowych dla dwóch zderzających się idealnie sprężyście kul. Te dwa równania są używane do określenia prędkości wypadkowych dwóch kul. Gdy obie kule ważą tyle samo, rozwiązanie jest proste: poruszająca się kula zatrzymuje się względem nieruchomej, a nieruchoma przejmuje całą prędkość początkową drugiej. Dzięki założeniu idealnie sprężystych zderzeń kul nie ma potrzeby uwzględniania strat energii cieplnej i akustycznej.
Podczas zderzeń kule stalowe ulegają niewielkim ściśnięciom, przy dużej sprężystości, dzięki czemu nie ma dużych strat w postaci ciepła.
Inne przykłady tego efektu.
Efekt wyrzucenia ostatniej kulki z prędkością prawie równą prędkości pierwszej kuli można zaobserwować podczas uderzeń szeregu monet ustawionych w linii prostej inną monetą o tej samej wartości, w wyniku czego ostatnia moneta odskakuje podobnie jak kule Newtona. Podobnym efektem jest uderzenie kuli bilardowej lub szeregu kul.
Przenoszenie pędu odbywa się bardzo szybko, niezauważalnie dla obserwatora. Dla stalowych kulek prędkość przekazu pędu równa jest prędkości podłużnej fali mechanicznej w stali, czyli około . Oszacuj po jakim czasie odskoczy szósta (ostatnia) kulka po uderzeniu pierwszej, jeżeli średnica każdej z kulek wynosi .
Rozwiązanie
Impuls musi pokonać drogę czterech kulek, aby odskoczyła ostatnia kulka:
.
Fala mechaniczna porusza się ruchem jednostajnym prostoliniowym czyli , a więc :
.
Jaką energię kinetyczną posiada kulka pierwsza o masie tuż przed zderzeniem, jeżeli różnica poziomów środków ciężkości od wychylenia do zderzenia wynosiła ? Przyjmij wartość przyspieszenia ziemskiego równą .
Rozwiązanie
Zgodnie z zasadą zachowania energii, kulka tuż przed zderzeniem posiada maksymalną energię kinetyczną, równą energii potencjalnej na najwyższym poziomie odchylenia środka ciężkości czyli na wysokości :
.
Energia kinetyczna kulki nr o masie tuż przed zderzeniem wynosiła .
Na jaką wysokość wzniesie się kulka nr o masie , jeżeli tuż przed odchyleniem miała maksymalną energię kinetyczną równą ? Przyjmij wartość przyspieszenia ziemskiego równą .
Rozwiązanie
Zaraz na początku ruchu kulka nr miała maksymalną energię kinetyczną i zgodnie z zasadą zachowania energii taką energię potencjalną kulka nr będzie posiadała przy najwyższym wzniesieniu, licząc poziomy środków ciężkości kulki nr i kulki nr :
Na jaką wysokość należy unieść kulkę pierwszą, aby kulka ostatnia odskoczyła z prędkością początkową równą ? Przyjmij wartość przyspieszenia ziemskiego równą .
Rozwiązanie
Multimedium - Symulacja
Za pomocą poniższej symulacji możesz zbadać energie wahadeł w zależności od ich wychylenia. Wybrane wahadła możesz wychylać na różne wysokości. Zwróć uwagę na punkty szczególne, w których albo energia kinetyczna, albo energia potencjalna jest maksymalna.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/P1Gz6l2JQ
Jaką zasadę i jakie wielkości fizyczne należy znać, aby wyznaczyć na jaką wysokość wzniesie się kulka nr ? Zaznacz trzy prawidłowe odpowiedzi.

Zadania
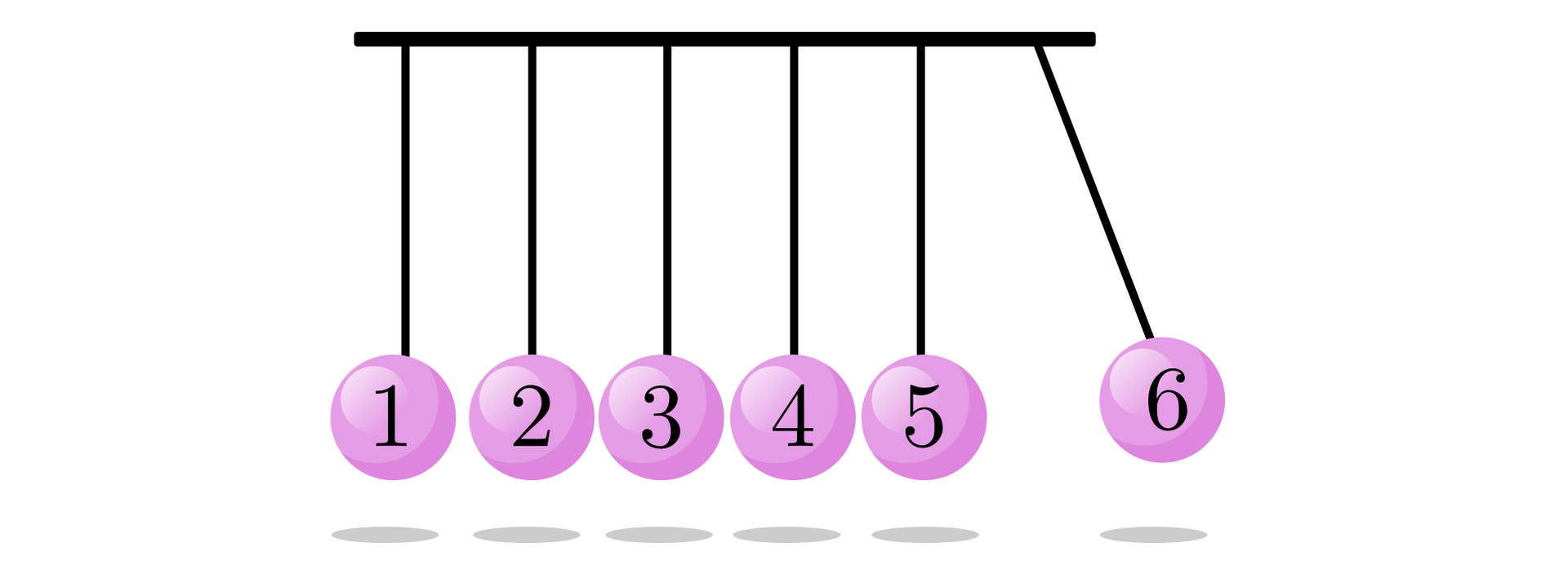
Poniższe ćwiczenia odnoszą się do kołyski Newtona z sześcioma wahadłami, ponumerowanymi kolejno od do .
Co się stanie, jeśli wychylimy skrajną kulkę nr , a następnie puścimy ją swobodnie? Odpowiedź zapisz w polu poniżej.
Co się stanie, jeśli wychylimy kulki –? Odpowiedź zapisz w polu poniżej.
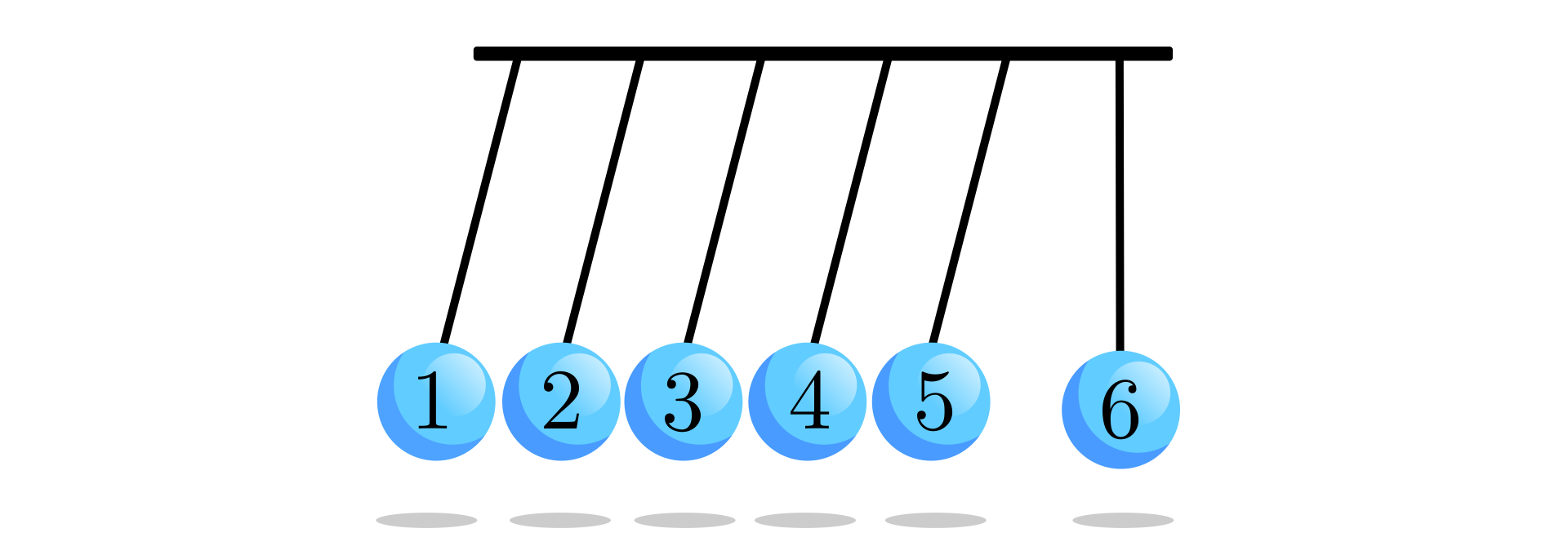
Jaka będzie główna różnica w zachowaniu między kołyskami z pięcioma a z sześcioma wahadłami, przy wychyleniu trzech kul –? Odpowiedź zapisz w polu poniżej.
Określ, jakie są podstawowe jednostki wysokości, prędkości, czasu i energii kinetycznej.
Słownik
wahadło Newtona, potocznie kulki Newtona – przyrząd ilustrujący zasadę zachowania energii i pędu podczas sprężystego zderzenia kul.