Wielokąty
2. Wielokąty foremne
Wielokąty foremne mają wiele ciekawych zastosowań w architekturze i sztuce. Na przestrzeni lat architekci różnych kultur tworzyli budowle, wykorzystujące wielokąty foremne jako podstawę do budowy ich konstrukcji.
Problemem związanym z klasycznymi konstrukcjami geometrycznymi, z którym częściej spotykają się współcześni adepci matematyki szkolnej, jest możliwość skonstruowania wielokąta foremnego. Dopiero w wieku matematyk niemiecki C.F. Gauss podał kryterium, które pozwala wskazać, które z wielokątów foremnych można skonstruować za pomocą cyrkla i liniału.
Z tego materiału dowiesz się czym jest wielokąt foremny i jak go rozpoznać oraz poznasz jego własności.
Zapoznaj się z poniższą animacją, aby poznać najczęściej spotykane wielokąty foremne.
Film dostępny pod adresem /preview/resource/R1bRDSumWAYrF
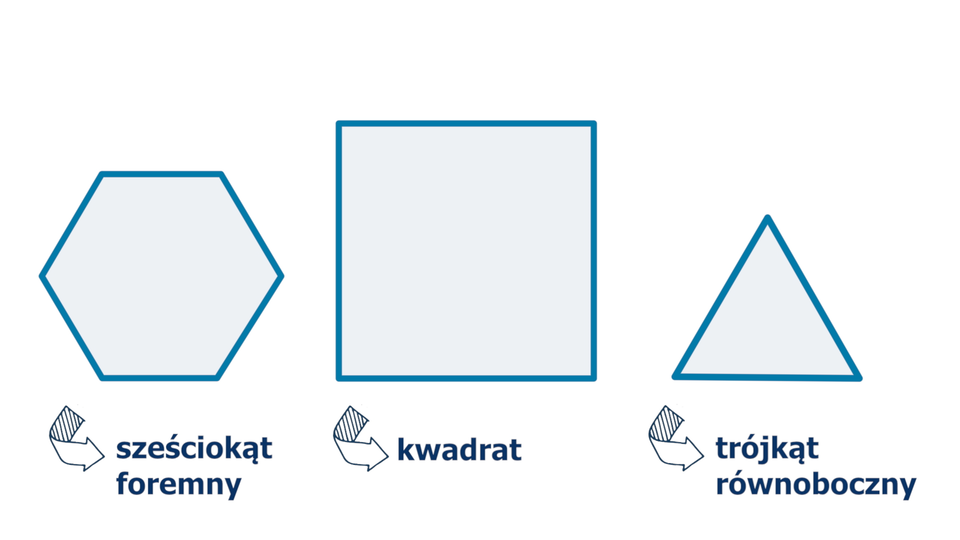
Animacja przedstawia przykłady wielokątów foremnych: sześciokąt foremny, kwadrat oraz trójkąt równoboczny.
Wielokątem foremnym nazywamy wielokąt, który ma wszystkie boki równe i wszystkie kąty równe.

Trójkąt foremny
Trójkąt równoboczny jest wielokątem, który ma wszystkie boki równe i wszystkie kąty równe.
Jest on przykładem wielokąta foremnego.
Tylko w trójkącie równobocznym punkt przecięcia się symetralnych oraz dwusiecznych leży w punkcie przecięcia wysokości.
Punkt przecięcia dzieli taki odcinek w stosunku , licząc od wierzchołka trójkąta.
Czworokąt foremny
Czworokąt, który jest wielokątem foremnym, to kwadrat.
Narysuj na kartce kwadrat i:
zaznacz jego przekątne,
wytnij ten kwadrat,
odrysuj go na kartce,
połóż wycięty kwadrat tak, aby pokrywał rysunek,
obróć wycięty kwadrat o wokół punktu przecięcia przekątnych,
obrysuj figurę, która powstała z kwadratu narysowanego i wyciętego.
Jak myślisz, czy powstały wielokąt jest wielokątem foremnym?
Pięciokąt foremny
Kolejnym wielokątem foremnym jest pięciokąt foremny.

Wielu wybitnych matematyków poszukiwało najprostszych sposobów konstrukcji tego wielokąta przy pomocy cyrkla i linijki. Poniżej przedstawiona jest jedna z najbardziej znanych konstrukcji. Spróbuj wykonać ją w zeszycie.
Film dostępny pod adresem /preview/resource/R207XCDAr0LtC
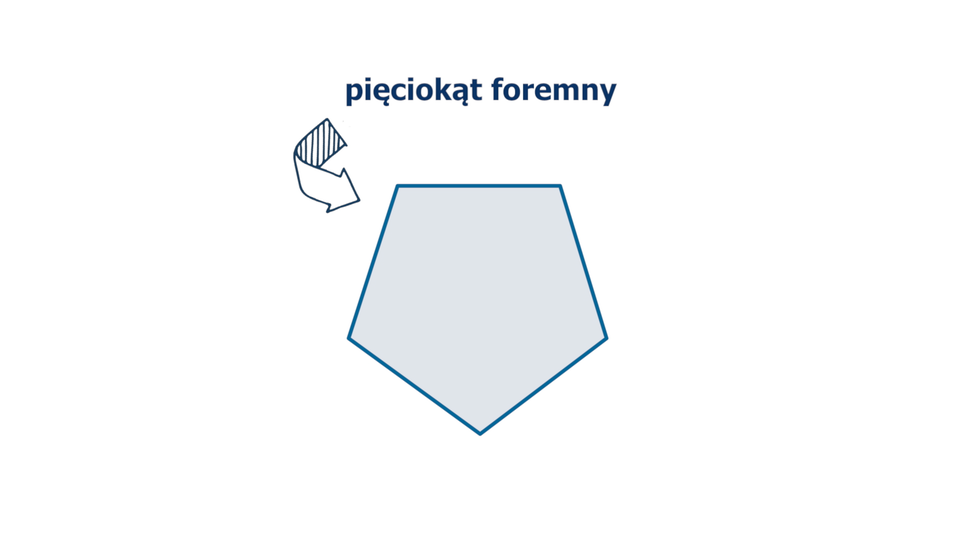
Animacja przedstawia kolejne etapy konstrukcji pięciokąta foremnego.
Obliczymy miary kątów pięciokąta.
W tym celu dzielimy go na trójkąty równoramienne.

Kąt miedzy równymi ramionami każdego z tych trójkątów to piąta część kąta .
Zatem kąt przy podstawie trójkąta:
Kąt pięciokąta jest dwukrotnie większy od kąta
Każdy kąt pięciokąta foremnego ma więc miarę .
Sześciokąt foremny
Zauważmy, że w trójkącie równobocznym każdy z kątów ma miarę . Możemy więc takie trójkąty ułożyć w ten sposób, aby miały jeden punkt wspólny tak, jak na rysunku.

Powstanie wtedy sześciokąt o równych bokach. Każdy kąt tego wielokąta ma miarę:
Jest to więc wielokąt foremny. Nazywamy go sześciokątem foremnym.
Zauważmy, że długość boku sześciokąta jest równa połowie dłuższej przekątnej.
Poniżej przedstawiona jest konstrukcja sześciokąta. Spróbuj wykonać ją w zeszycie.

Film dostępny pod adresem /preview/resource/RqUVjbeHQkHko
Animacja przedstawia konstrukcję sześciokąta foremnego za pomocą cyrkla i linijki.
Siedmiokąt foremny
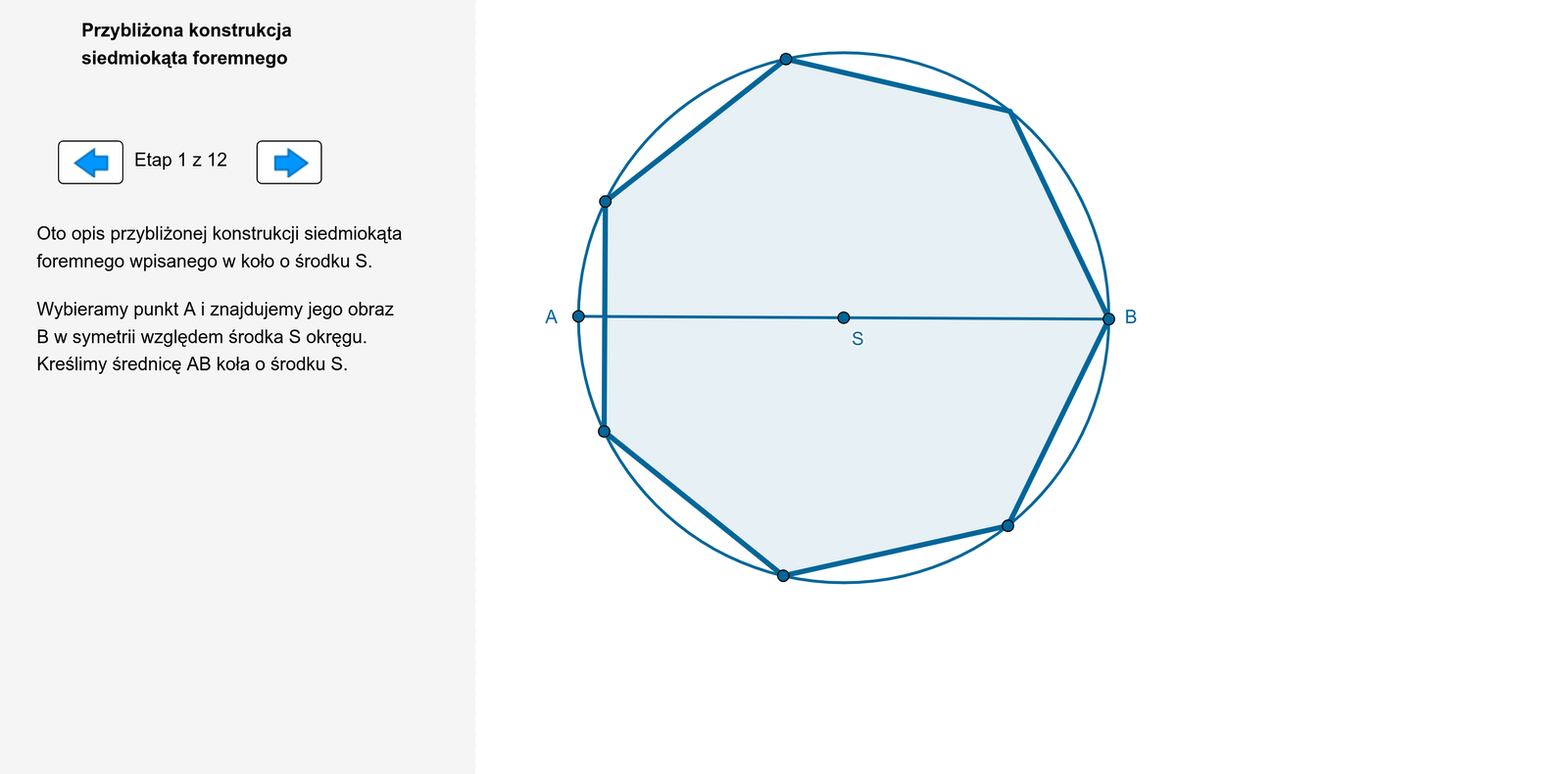
Siedmiokąt można narysować, wykorzystując konstrukcję neusis [njusis], co oznacza po grecku „dopasowanie”. Jest to konstrukcja geometryczna, w której, w odróżnieniu od konstrukcji klasycznej, oprócz cyrkla używa się linijki z podziałką (z dwoma zaznaczonymi punktami).

Siedmiokąt foremny jest przykładem wielokąta foremnego, którego nie można skonstruować jedynie za pomocą linijki i cyrkla. Udowodnił to wybitny niemiecki matematyk Karol Gauss [Karol Gaus] ( – ), który tym samym położył kres wielowiekowym wysiłkom matematyków próbujących znaleźć taką konstrukcję.
Zapoznaj się z poniższym apletem.
Zapoznaj się z opisem poniższego apletu.
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DkXZWHm0e
Własności wielokąta foremnego:
wszystkie boki równe,
wszystkie kąty równe,
przekątne nie muszą być równe.
Wielokąty gwiaździste
Wykorzystując niektóre wielokąty foremne, można budować wielokąty, zwane gwiaździstymi.
Najpopularniejszym z nich jest pięciokąt gwiaździsty znany od czasów starożytnych pod nazwą pentagramu. Rysunek pentagramu był znakiem rozpoznawczym uczniów Pitagorasa.

Na bazie siedmiokąta można wykreślić siedmiokąt gwiaździsty zwany z greckiego heptagramem.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DkXZWHm0e
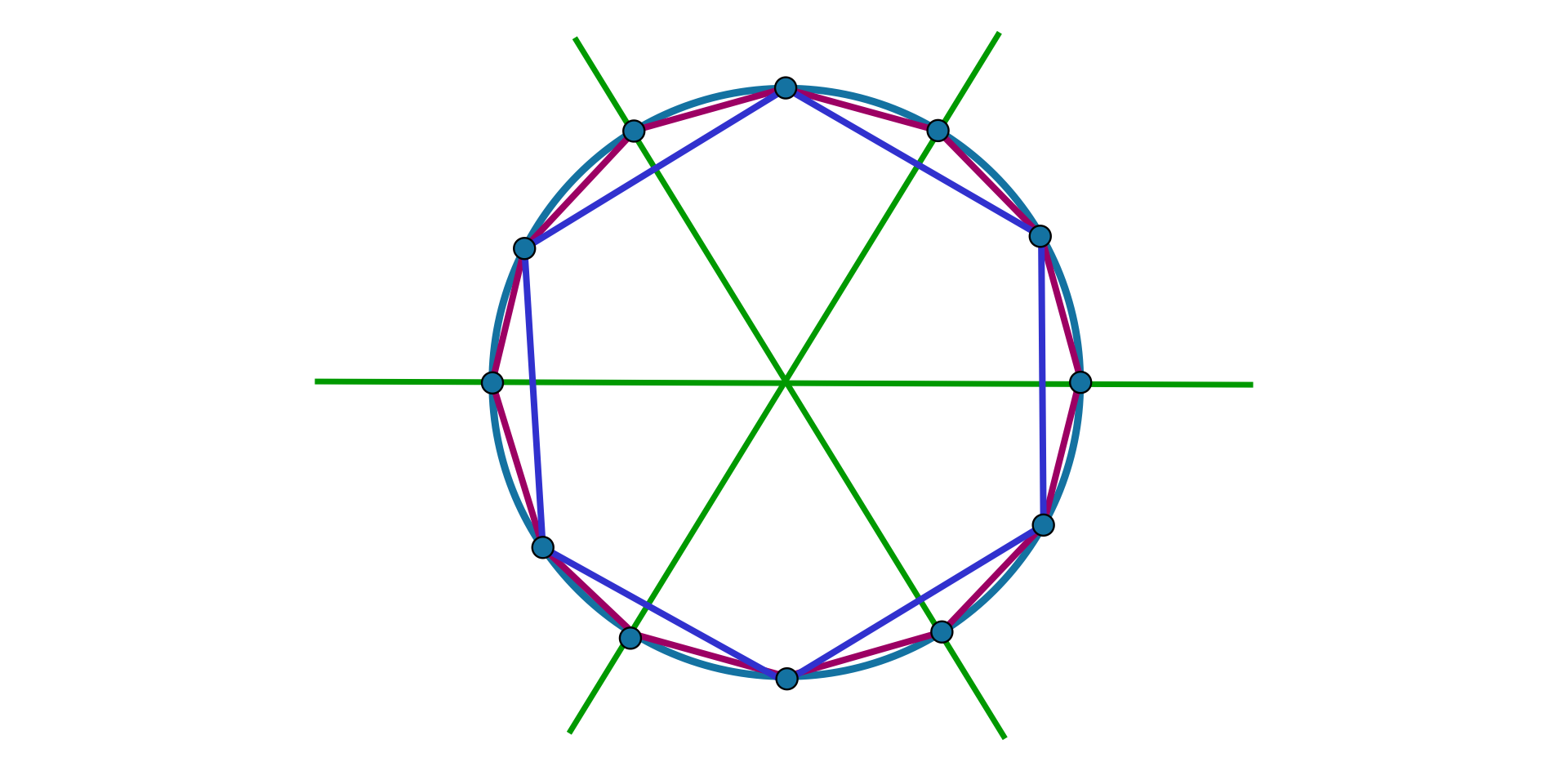
Tworząc formy gwiaździste, kreślimy przekątne wielokąta, omijając za każdym razem tę samą liczbę wierzchołków. Inną gwiazdę otrzymamy, gdy będziemy omijać dwa wierzchołki, inną, gdy trzy.
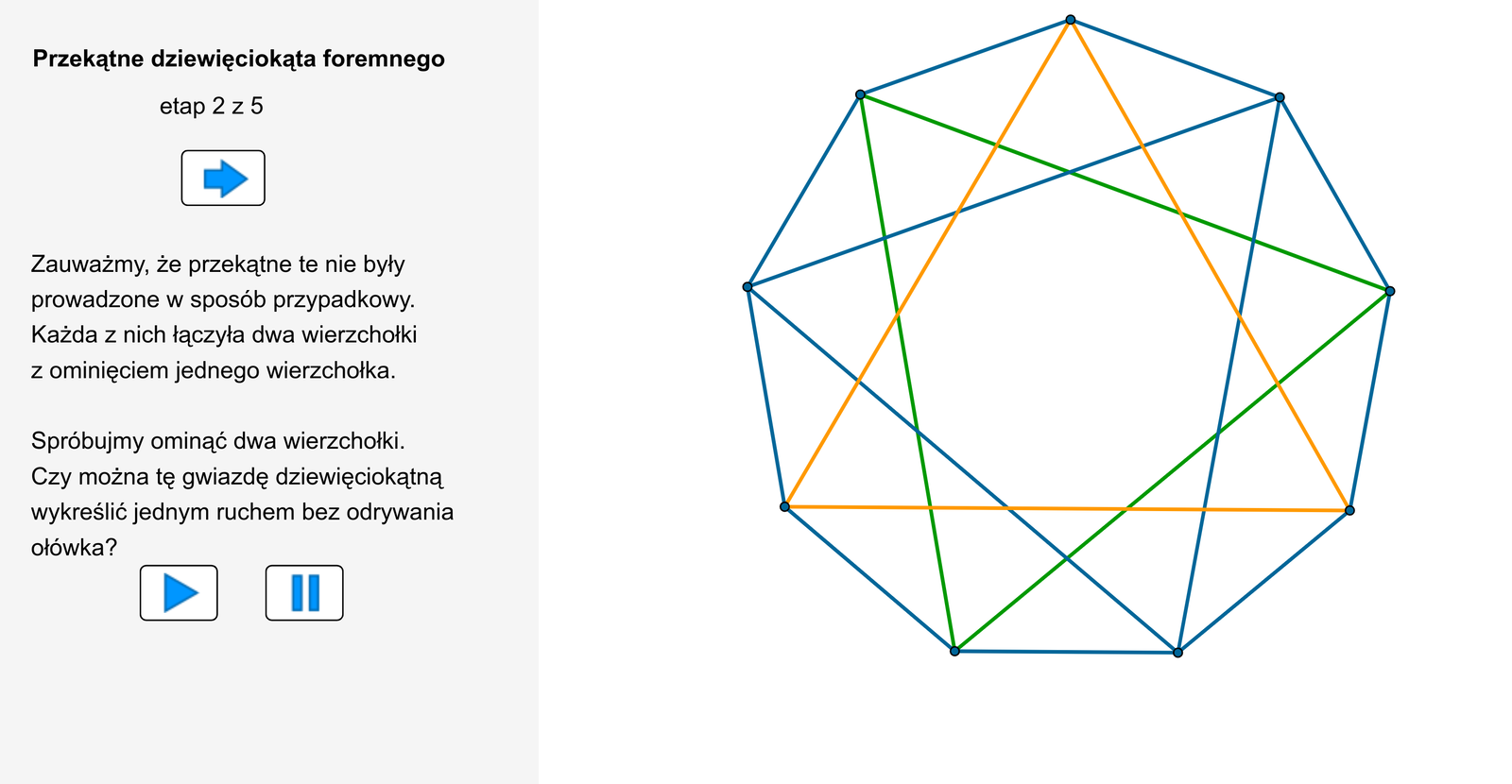
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DkXZWHm0e
Zastanówmy się, czy wielokąty foremne są figurami środkowosymetrycznymi. Sprawdzimy to, wykorzystując poniższy aplet.
Przesuwając punkty odpowiednio , , po bokach wielokątów, obserwujemy zmianę położenia punktów , , . Punkty , , są obrazami punktów , , w symetrii środkowej o środkach w punktach , , odpowiednio.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DkXZWHm0e
Zauważmy, że środek symetrii mają tylko wielokąty foremne o parzystej liczbie wierzchołków.
Większość ciał stałych ma budowę krystaliczną. Charakteryzuje się ona regularnym ułożeniem atomów, które tworzą tzw. siatkę krystaliczną. Bardzo często atomy w krysztale ułożone są w wierzchołkach wielokątów foremnych, a te z kolei tworzą struktury mające kształt brył nazywanych wielościanami foremnymi.
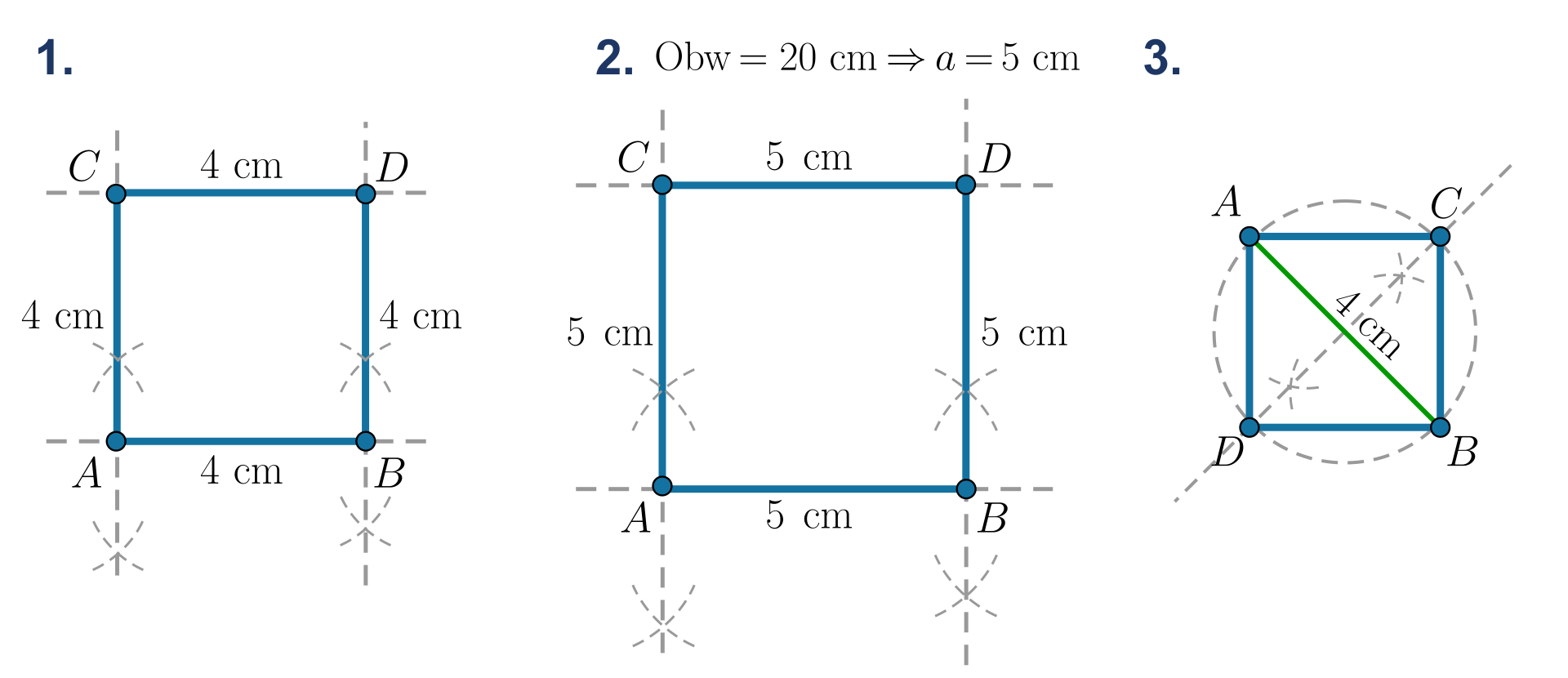
Skonstruuj kwadrat
o boku długości ,
którego obwód jest równy ,
którego przekątna ma długość .
Odpowiedz na pytania.
Czy wielokąty foremne są osiowosymetryczne?
Ile osi symetrii ma trójkąt równoboczny?
Ile osi symetrii ma kwadrat? A ile pięciokąt foremny?
Ile osi symetrii ma – kąt foremny?
Skonstruuj sześciokąt foremny.
Wykorzystując konstrukcję sześciokąta foremnego, skonstruuj dwunastokąt foremny.
Czy na podstawie sześciokąta foremnego można skonstruować dwunastokąt foremny?
- Wielokąt, który ma wszystkie boki równe jest wielokątem foremnym.
- Wielokąt, który ma wszystkie kąty równe jest wielokątem foremnym.
- Czworokąt foremny ma środek symetrii.
- Sześciokąt foremny ma środek symetrii.
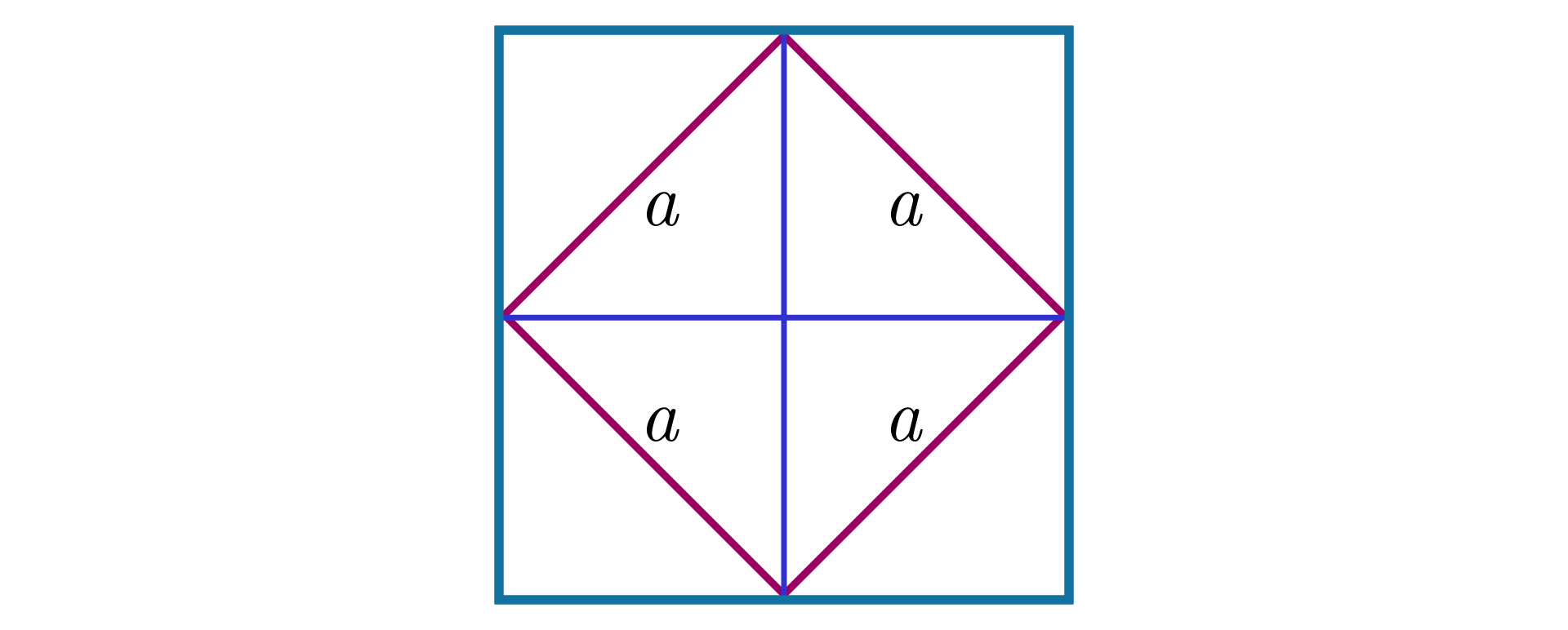
Narysuj kwadrat. Zaznacz środki jego boków. Połącz zaznaczone punkty tak, aby otrzymać czworokąt. Czy otrzymany czworokąt jest wielokątem foremnym? Dlaczego?
W narysowanym kwadracie zaznaczono środki jego boków i połączono zaznaczone punkty tak, że otrzymano czworokąt. Czy otrzymany czworokąt jest wielokątem foremnym? Dlaczego?
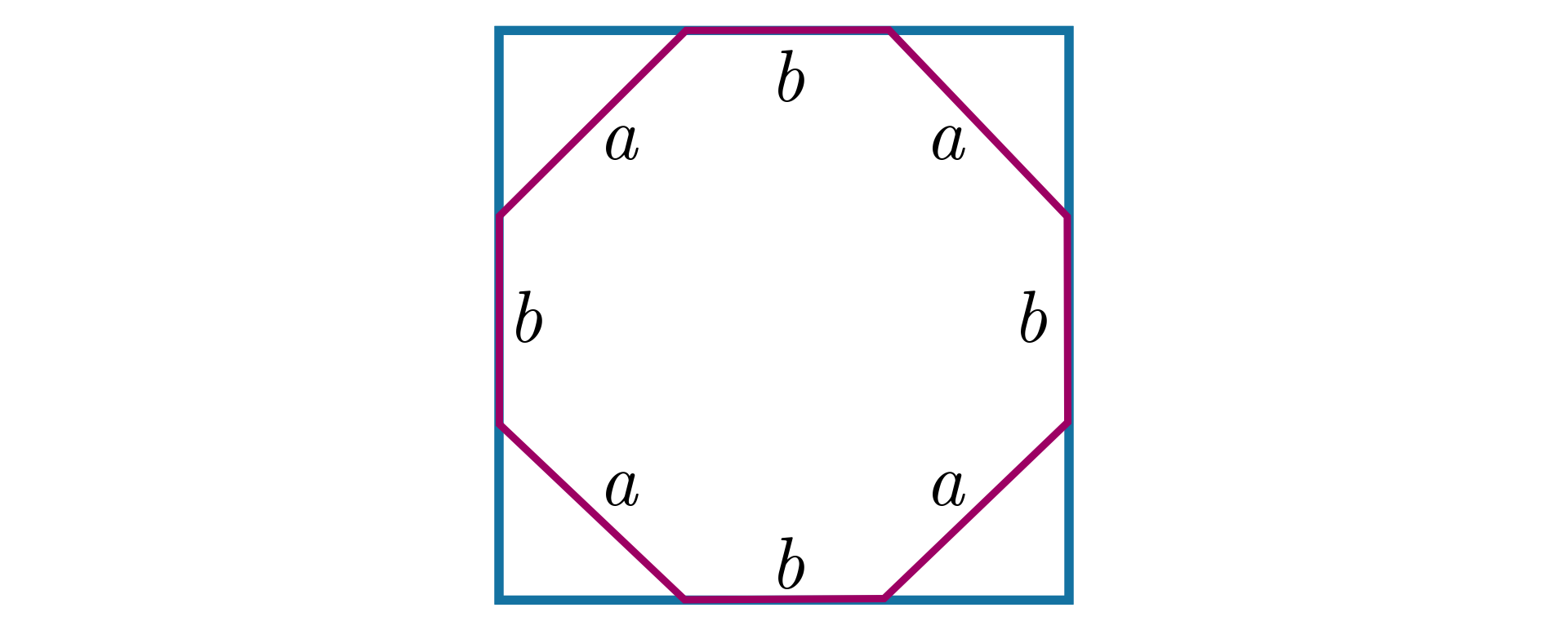
Narysuj kwadrat. Podziel każdy z jego boków na trzy równe części. Połącz punkty podziału tak, aby otrzymać ośmiokąt. Czy otrzymany ośmiokąt jest wielokątem foremnym? Dlaczego?
W narysowanym kwadracie podzielono każdy z jego boków na trzy równe części i połączono punkty podziału tak, że otrzymano ośmiokąt. Czy otrzymany ośmiokąt jest wielokątem foremnym? Dlaczego?
Narysuj trójkąt równoboczny. Zaznacz środki jego boków. Połącz zaznaczone punkty tak, aby otrzymać trójkąt. Czy otrzymany trójkąt jest wielokątem foremnym? Dlaczego?
W narysowanym trójkącie równobocznym zaznaczono środki jego boków i połączono je tak, że otrzymano trójkąt. Czy otrzymany trójkąt jest wielokątem foremnym? Dlaczego?
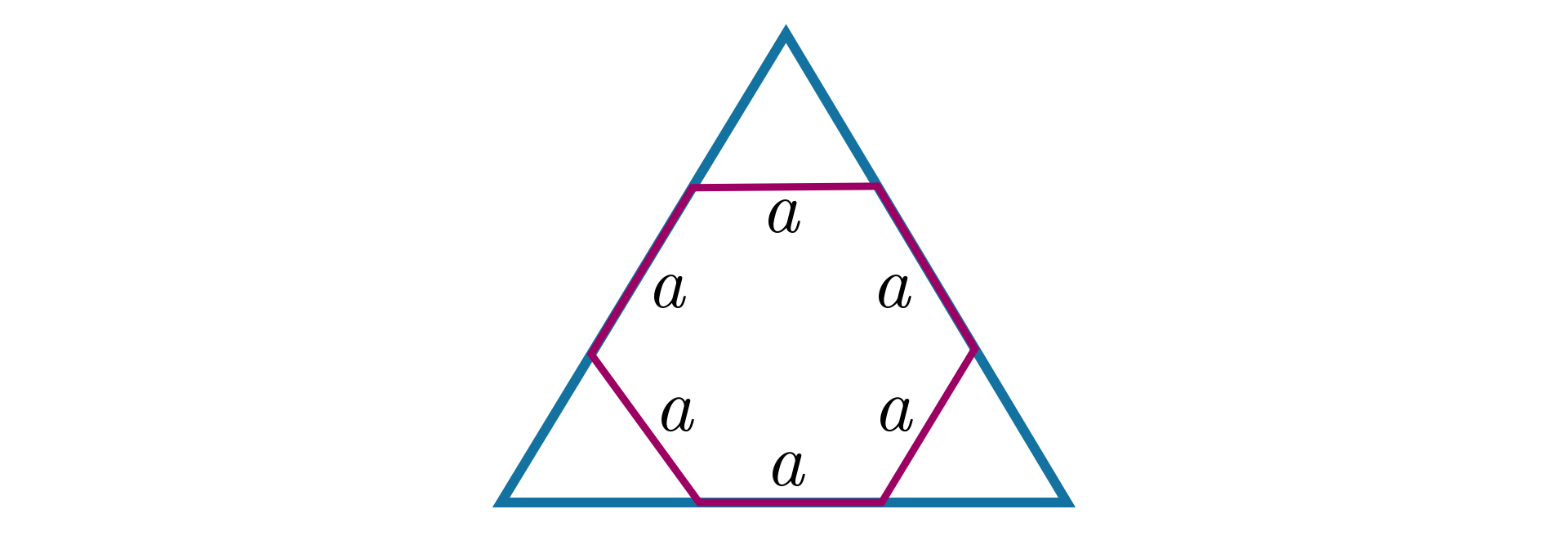
Narysuj trójkąt równoboczny. Podziel każdy z jego boków na trzy równe części. Połącz punkty podziału tak, aby otrzymać sześciokąt. Czy otrzymany sześciokąt jest wielokątem foremnym? Dlaczego?
W narysowanym trójkącie równobocznym podzielono każdy z jego boków na trzy równe części i połączono punkty podziału tak, że otrzymano sześciokąt. Czy otrzymany sześciokąt jest wielokątem foremnym? Dlaczego?
Notatnik
Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.