Symetrie
1. Symetralna odcinka
Dwie miejscowości – Kotlinka i Górka żyją od wielu lat we wzajemnym przymierzu. Aby to uhonorować, prezydenci miast postanowili postawić pomnik tak, aby z każdej miejscowości mieszkańcy mieli tak samo daleko do niego. Jak myślisz - w którym miejscu należałoby wybudować pomnik?

Aby odpowiedzieć na to pytanie, należy na planie znaleźć miejsce geometryczne punktu leżącego w tej samej odległości od punktu i od punktu .
W odnalezieniu tego punktu pomoże nam narysowanie symetralnej odcinkasymetralnej odcinka .
W dalszej części materiału zostanie przedstawione rozwiązanie tego problemu.
Czym jest symetralna odcinkasymetralna odcinka i jakie ma własności, dowiesz się, analizując przykłady zmieszczone w tym materiale.
Zaopatrz się w linijkę i cyrkiel i postępuj według instrukcji przedstawionej w poniższej tabeli.
Co musisz zrobić | Co otrzymasz |
|---|---|
Narysuj odcinek . |  Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0. |
Z punktów i zakreśl łuki o tym samym promieniu tak, aby przecięły się. | 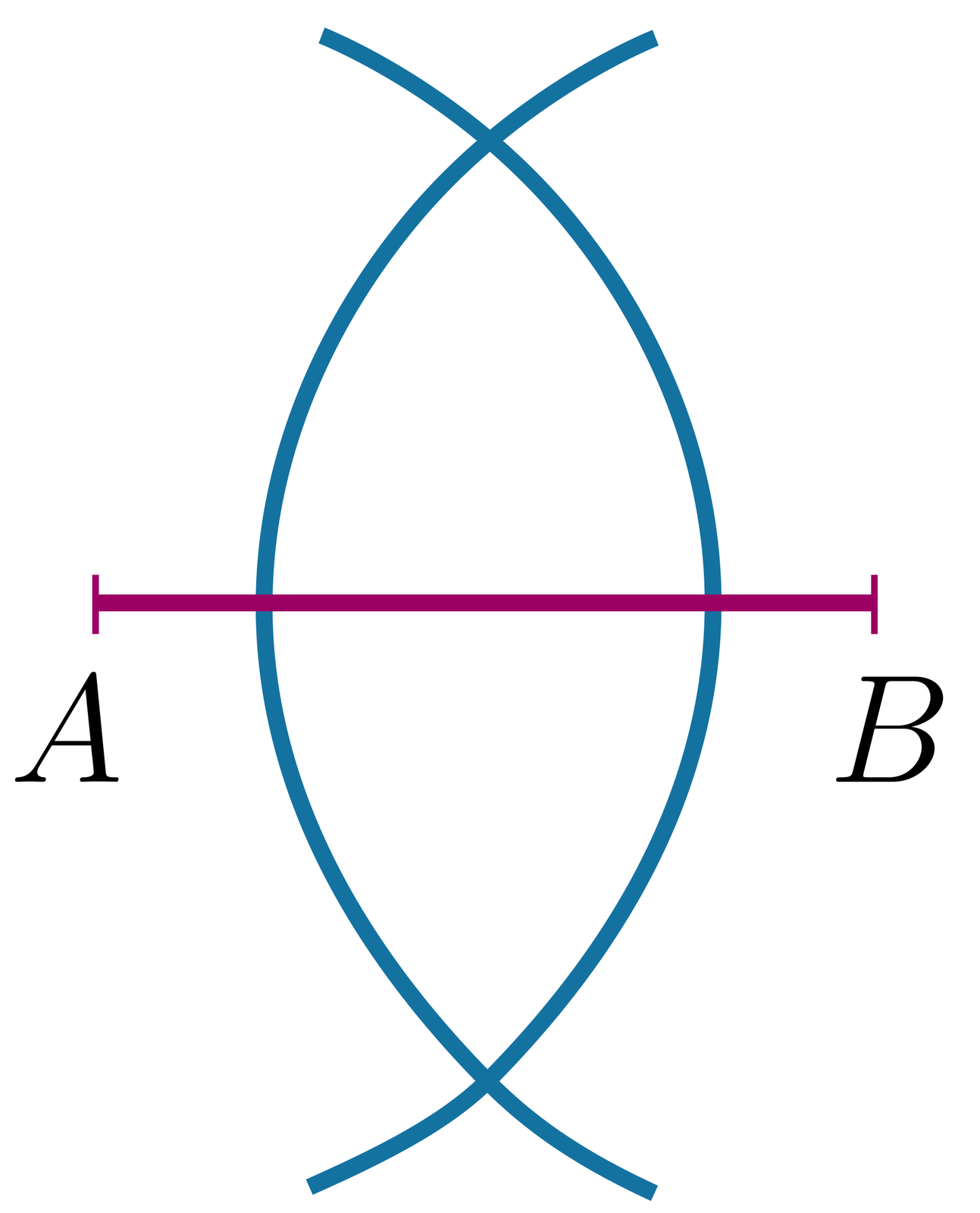 Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0. |
Przez otrzymane punkty przecięcia poprowadź prostą. | 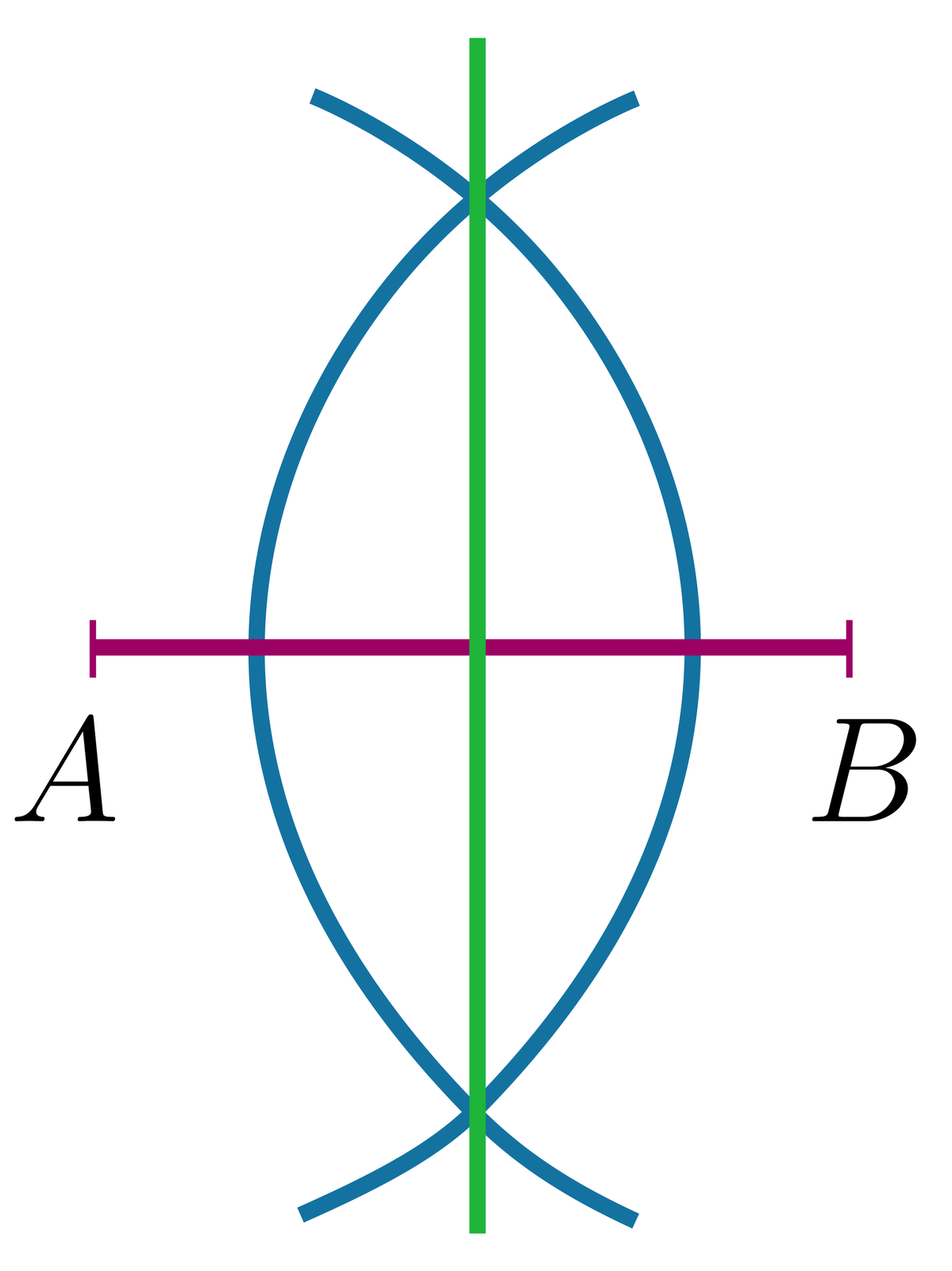 Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0. |
Prosta, otrzymana w wyniku konstrukcji dzieli odcinek na dwie równe części i jest prostopadła do tego odcinka. Jest to symetralna odcinkasymetralna odcinka .
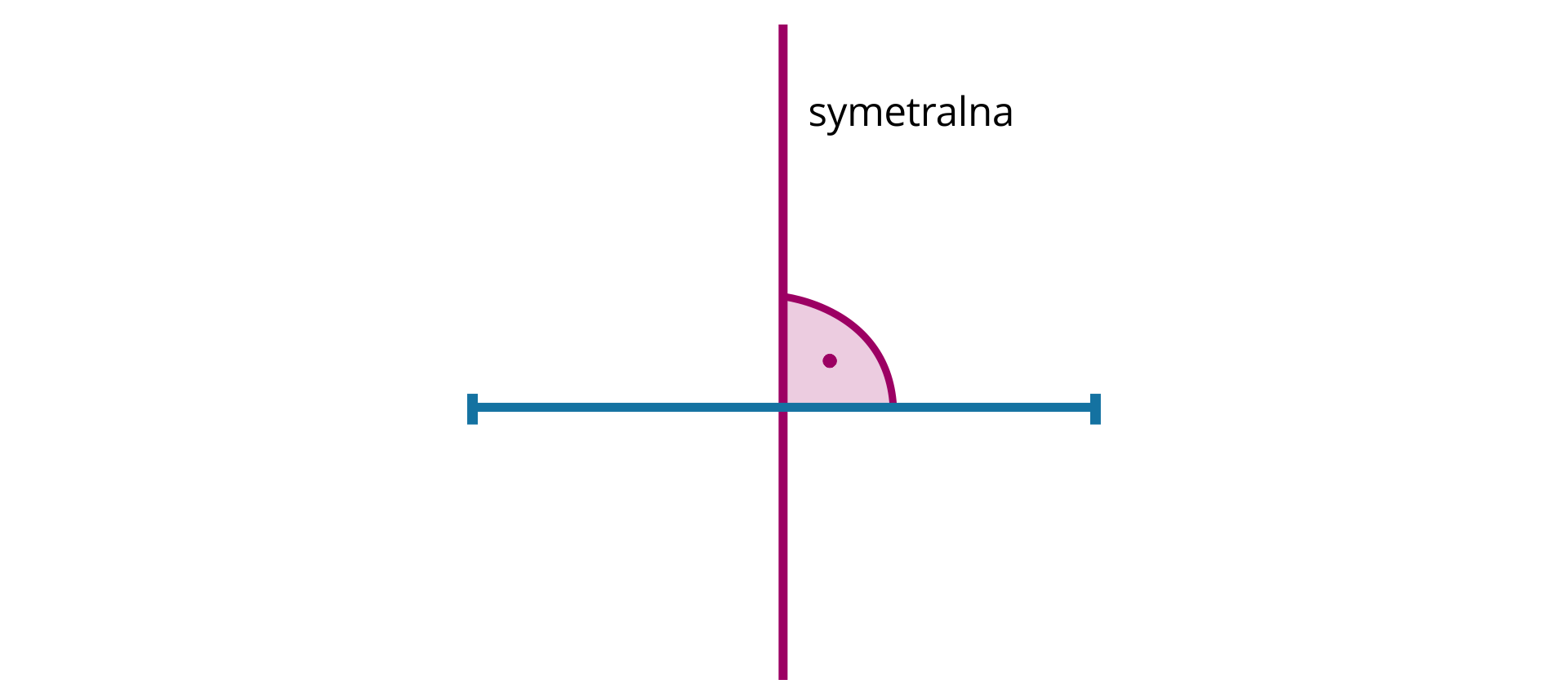
Symetralną odcinka nazywamy prostą prostopadłą do tego odcinka i przechodzącą przez jego środek.
Poniższy film przedstawia konstrukcję symetralnej odcinka.

Film dostępny pod adresem /preview/resource/R1ZqlyrA2bc1A
Animacja przedstawia w jaki sposób możemy skonstruować symetralną odcinka AB.
Podzielimy odcinek na cztery równe części.
Aby znaleźć punkty podziału, dzielimy najpierw odcinek za pomocą symetralnej na dwie równe części, a następnie każdą z tak otrzymanych części ponownie dzielimy na pół.
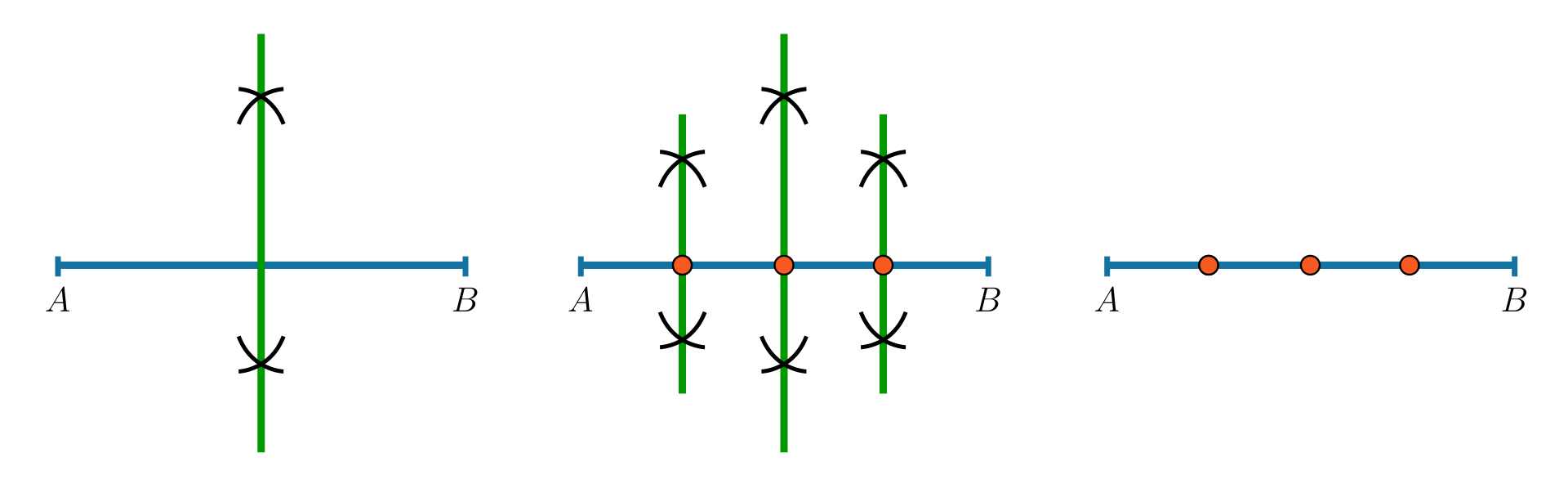
Za pomocą symetralnej możemy również podzielić odcinek na części w danym stosunku.
Narysujemy dowolny odcinek i podzielimy go w stosunku .
Postępujemy podobnie, jak w Przykładzie . Dzielimy odcinek na równych części.
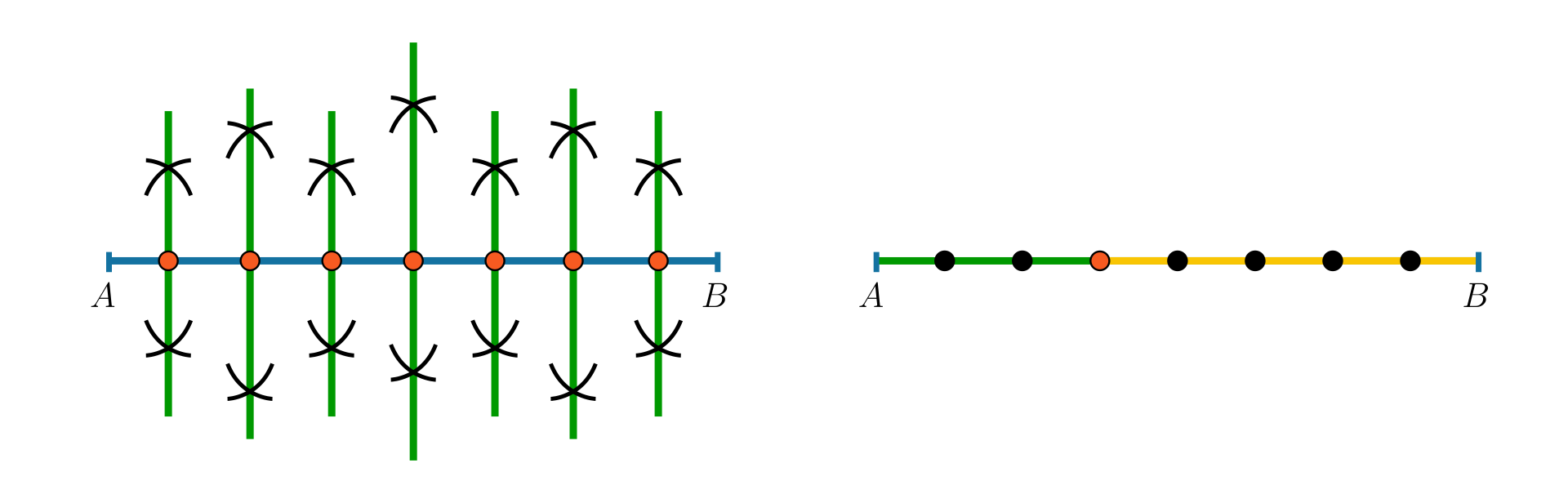
Pierwsze trzy części podziału to całego odcinka. Pozostałe pięć części to całego odcinka.
Na rysunku tylko prosta jest symetralną odcinkasymetralną odcinka .
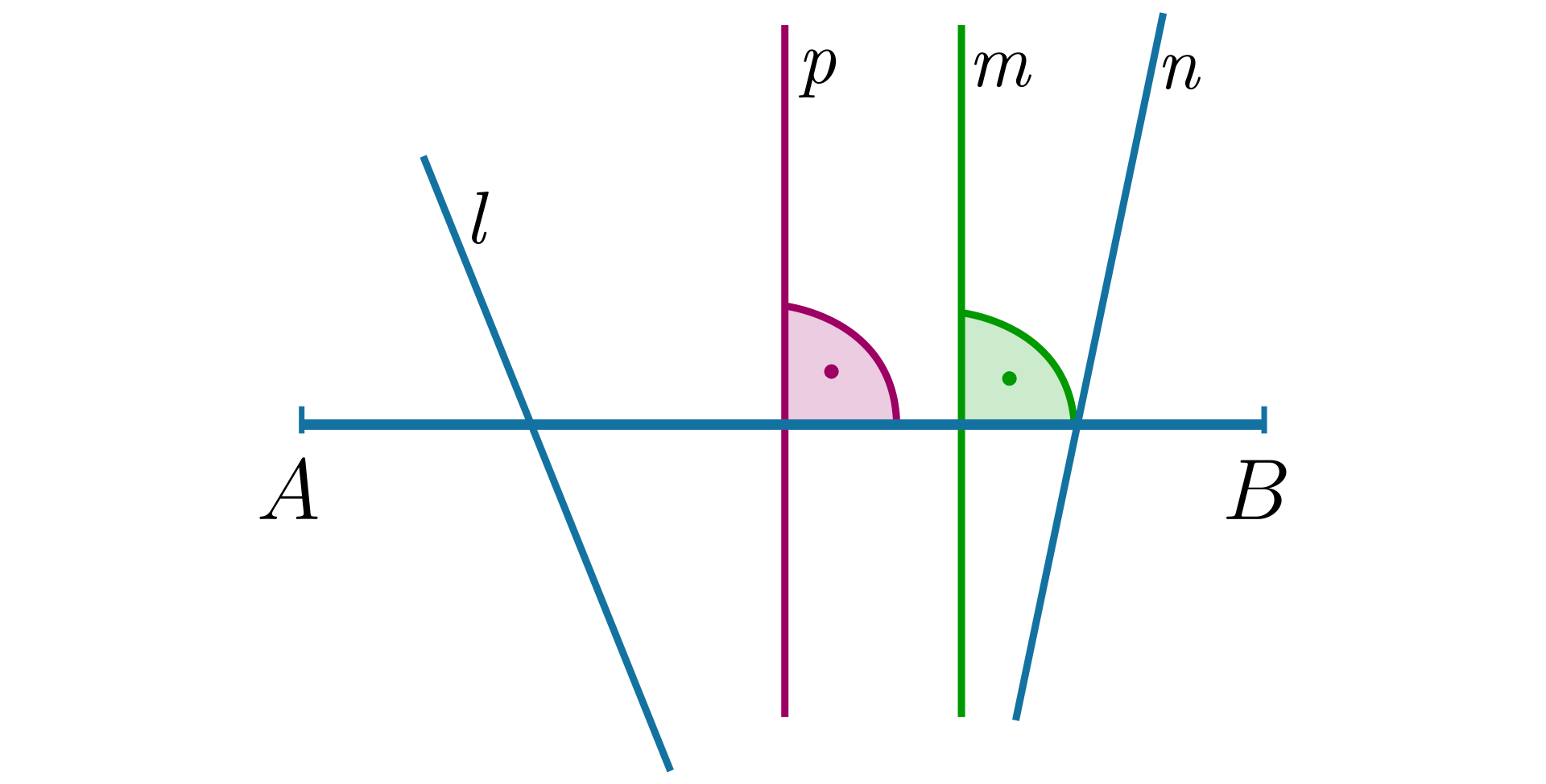
Symetralna odcinkaSymetralna odcinka jest zbiorem punktów równo odległych od końców tego odcinka.
Wynika z tego, że jeżeli punkt leży na symetralnej odcinkasymetralnej odcinka , to jego odległość od punktu jest taka sama jak odległość od punktu .
Zachodzi też własność odwrotna – każdy punkt płaszczyzny równo odległy od punktów i należących do tej płaszczyzny, leży na symetralnej odcinkasymetralnej odcinka .
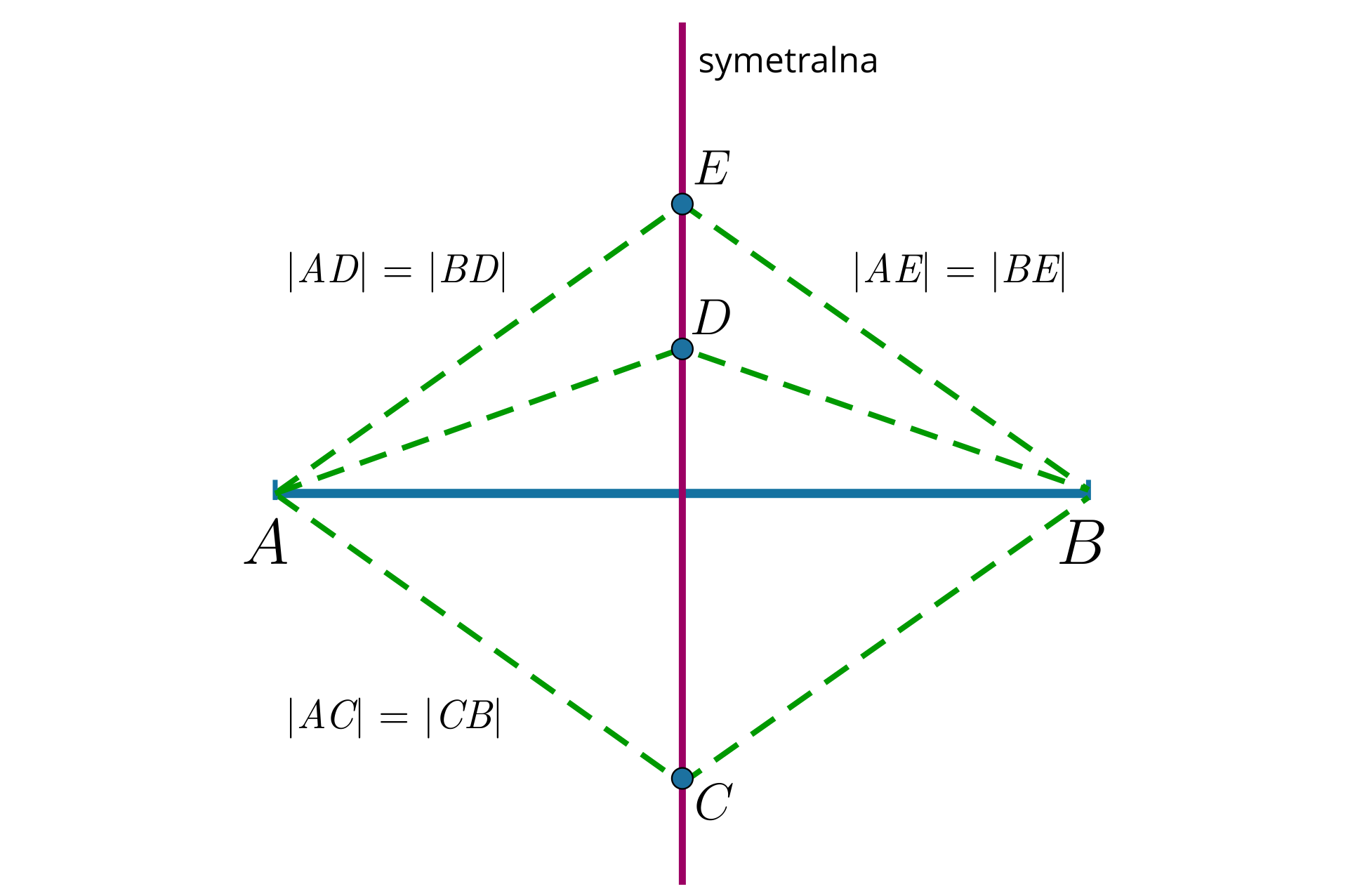
Odcinek ma tylko jedną symetralną.
Każdy z punktów leżących na symetralnej odcinka jest równo oddalony od obu końców tego odcinka.
Rozwiążemy teraz problem, zamieszczony na początku materiału.
Dwie miejscowości – Kotlinka i Górka żyją od wielu lat we wzajemnym przymierzu. Aby to uhonorować, prezydenci miast postanowili postawić pomnik tak, aby z każdej miejscowości mieszkańcy mieli tak samo daleko do niego. Jak myślisz - w którym miejscu należałoby wybudować pomnik?
Skorzystamy z tego, że punkt równo odległy od końców danego odcinka leży na symetralnej odcinkasymetralnej odcinka.
Tworzymy więc odcinek, którego końcami są punkty i , symbolizujące miejscowości Kotlinka i Górka. A następnie konstruujemy symetralną odcinkasymetralną odcinka .
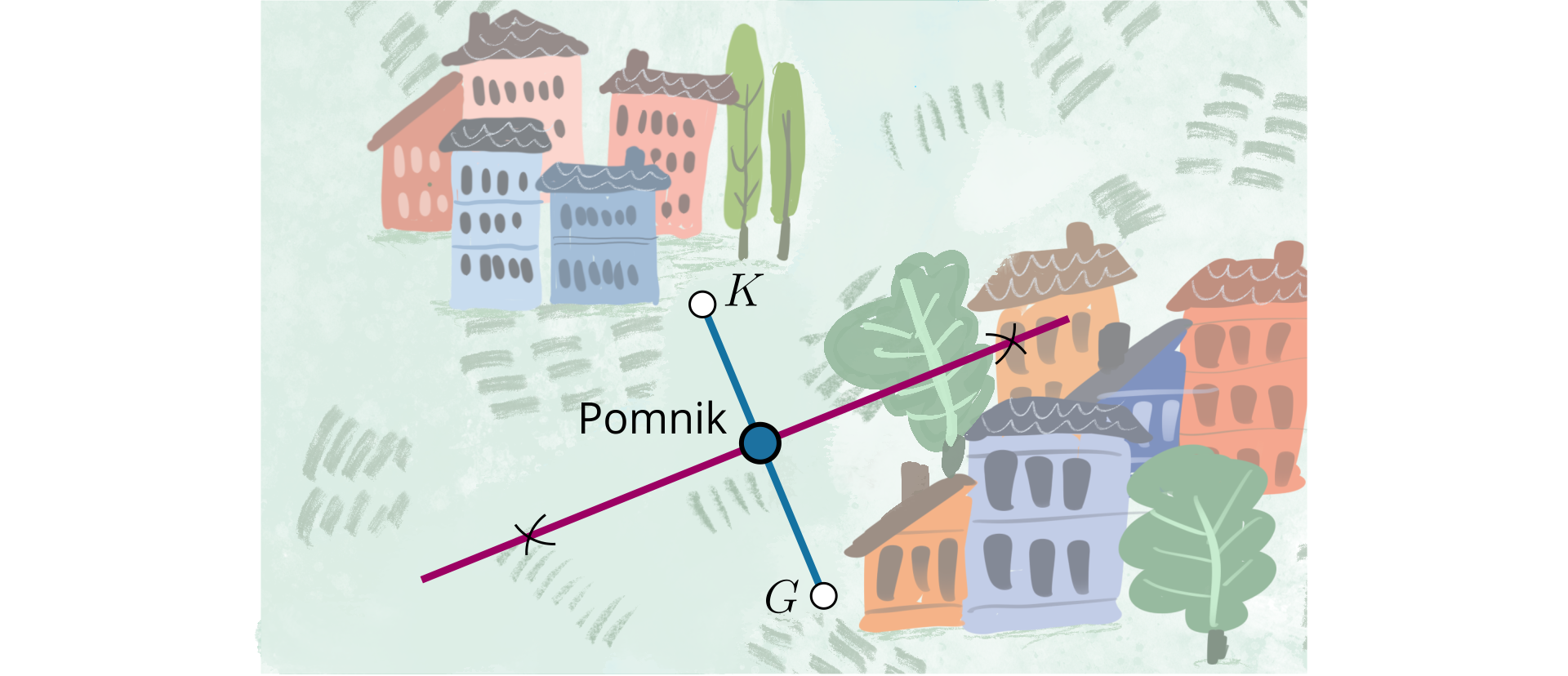
Punkt wspólny symetralnej i odcinka , będzie miejscem, w którym należy wybudować pomnik.
Proste i są symetralnymi dwóch cięciw okręgu. Uzasadnimy, że punkt przecięcia tych symetralnych jest środkiem okręgu.
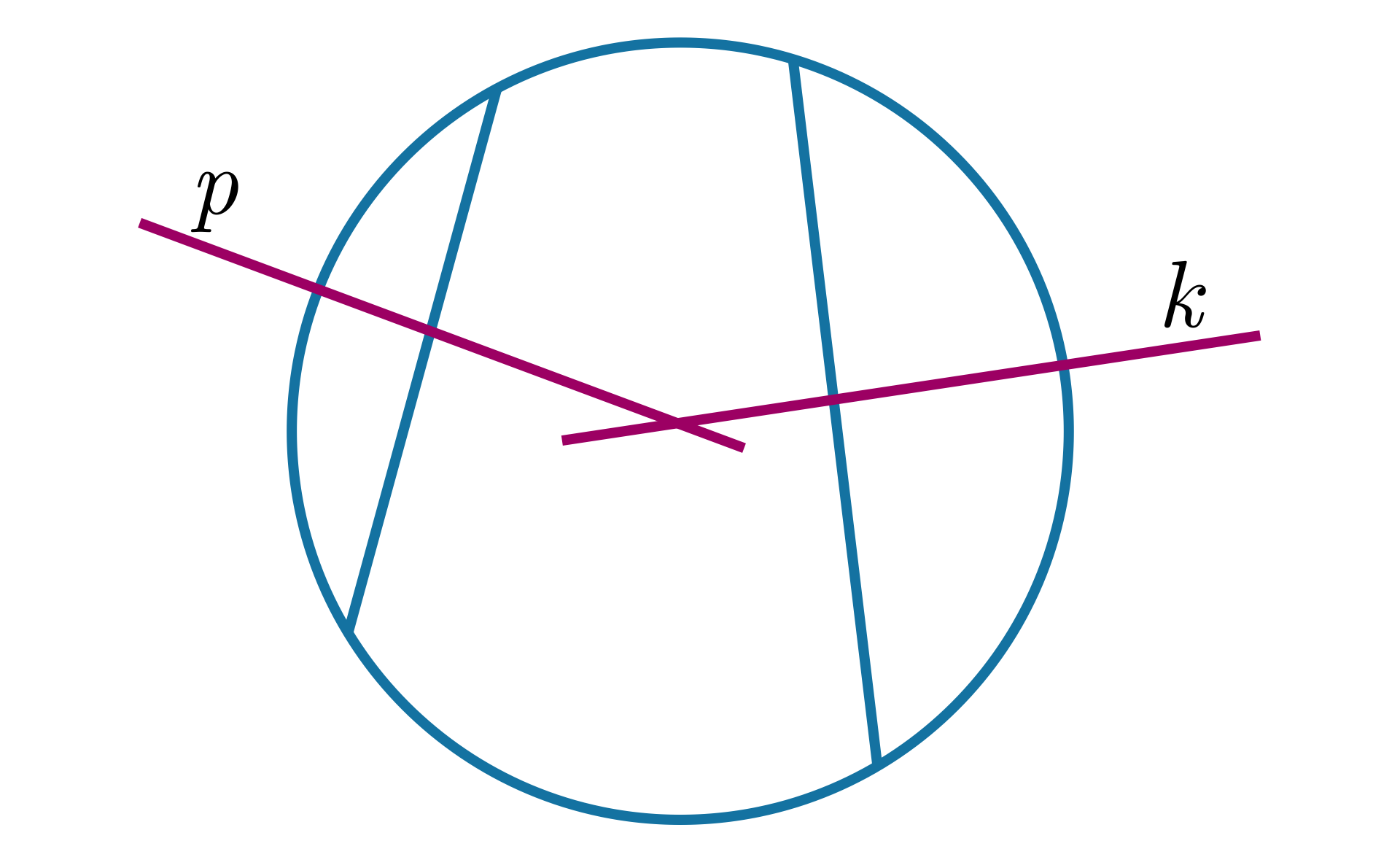
Wprowadźmy oznaczenia takie, jak na rysunku, gdzie i to cięciwy okręgu, – punkt przecięcia symetralnych tych cięciw.
Zaznaczone cięciwy nie są do siebie równoległe, zatem ich proste symetralne przecinają się w jednym punkcie.
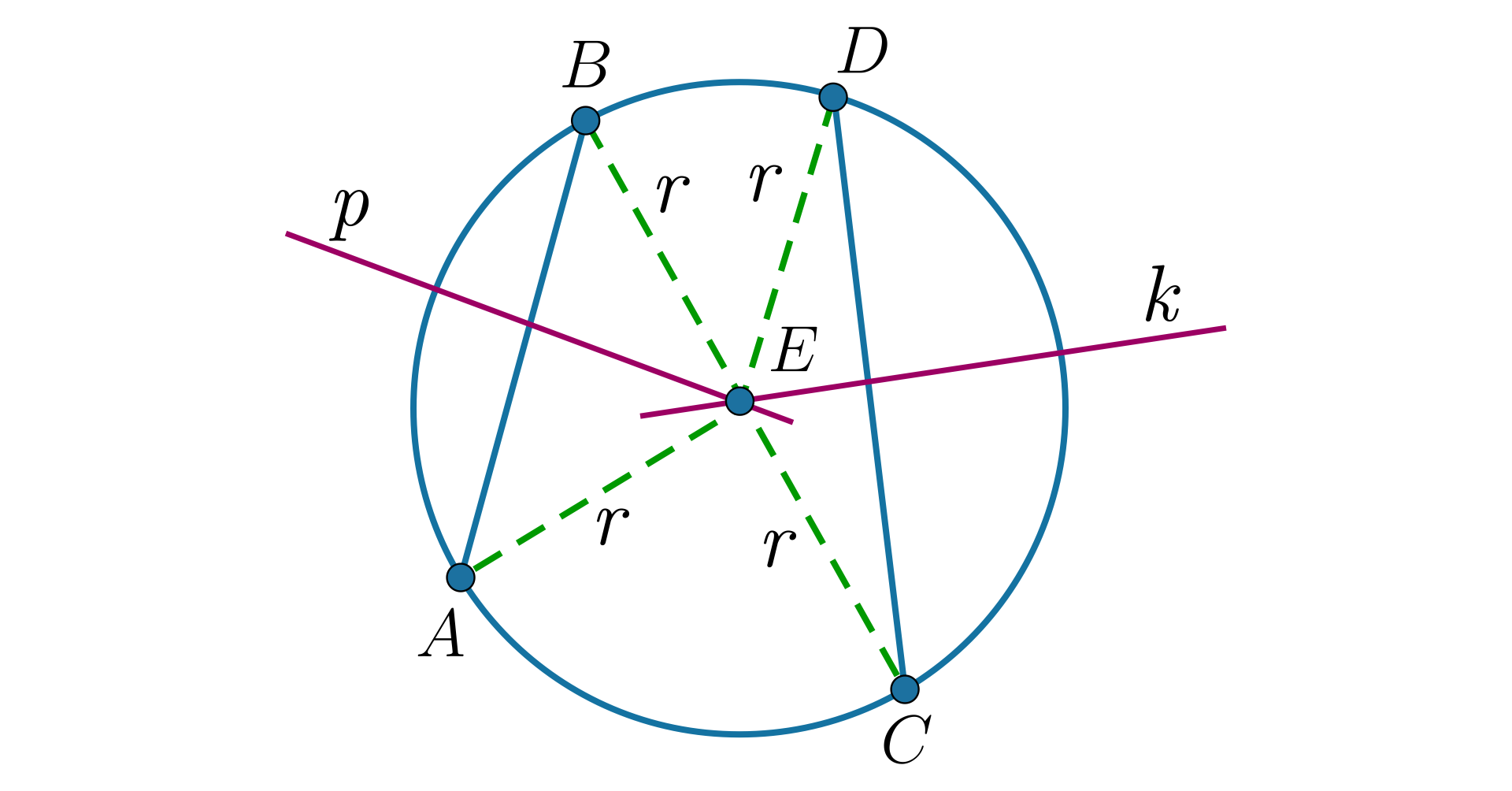
Wiadomo, że symetralna dowolnej cięciwy przechodzi przez środek okręgu. Wynika to z faktu, iż środek okręgu jest równoodległy od końców cięciwy, zatem leży na jej symetralnej.
Punkt należy zarówno do symetralnej cięciwy , jak i do symetralnej cięciwy .
Zatem wynika stąd, że punkt przecięcia prostych symetralnych wyznacza środek okręgu.
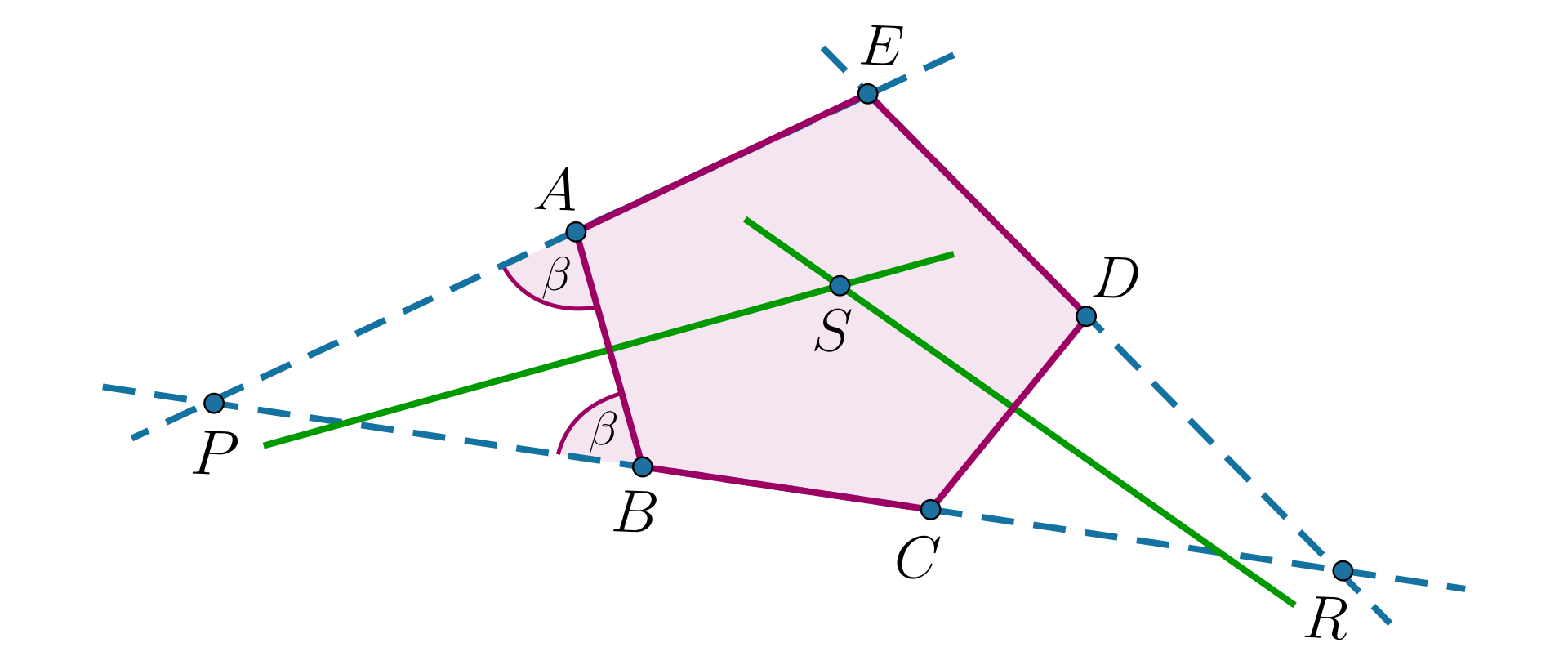
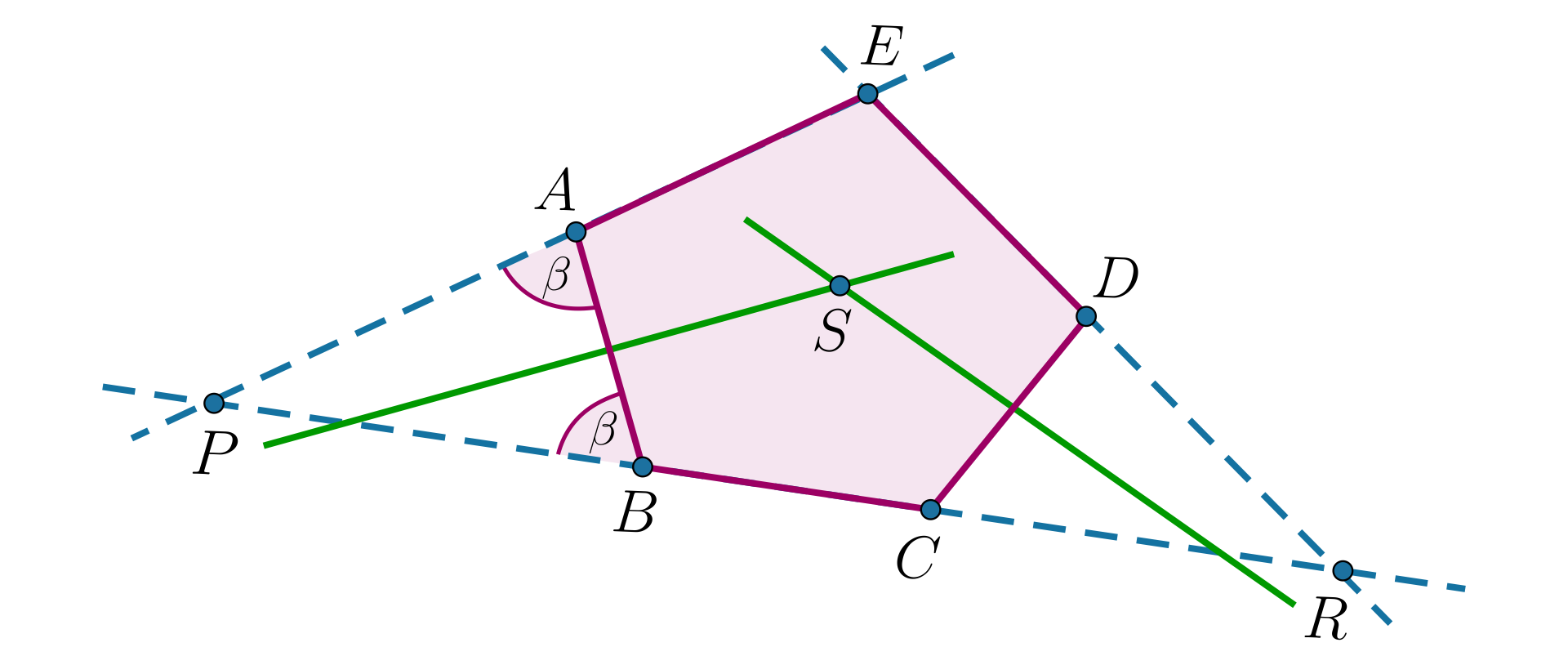
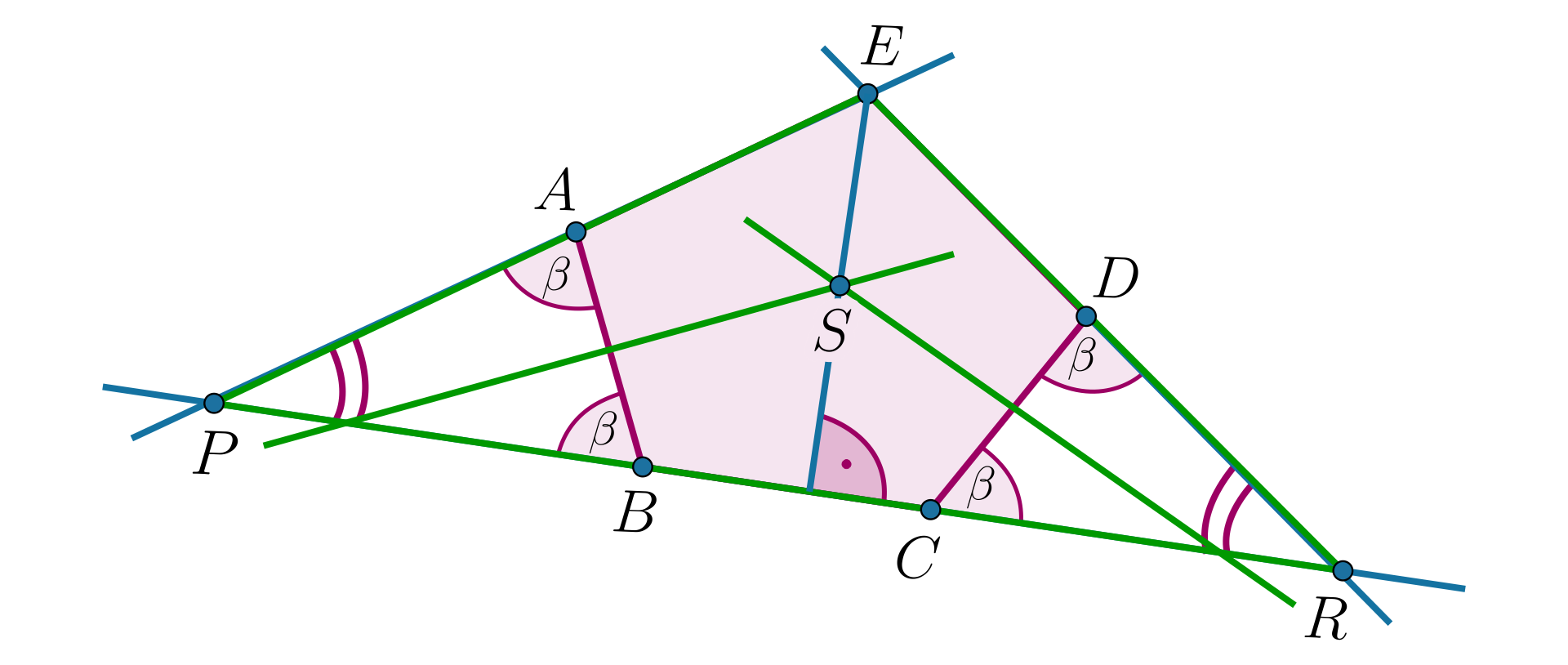
Dany jest pięciokąt . Prosta jest symetralną odcinkasymetralną odcinka oraz i .
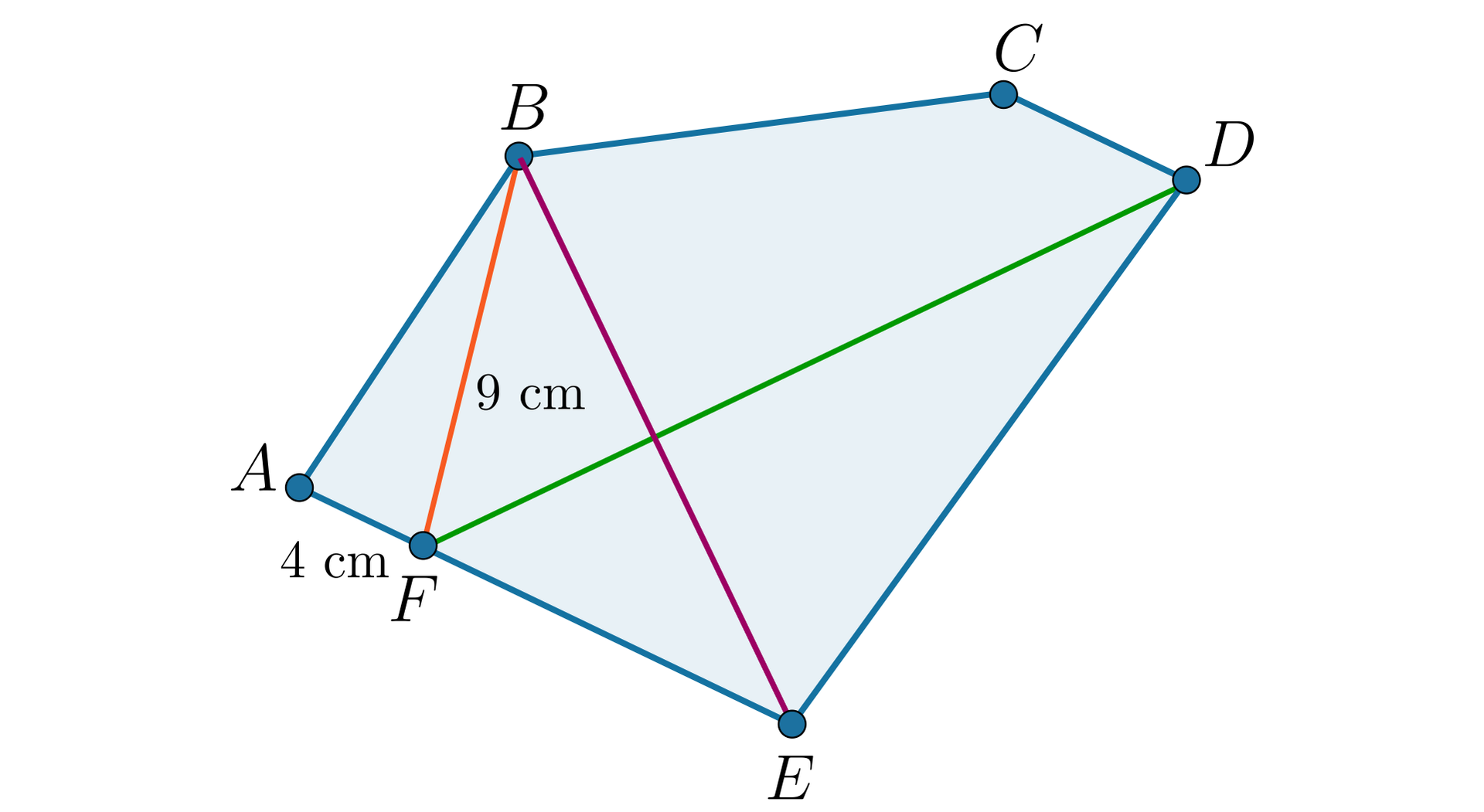
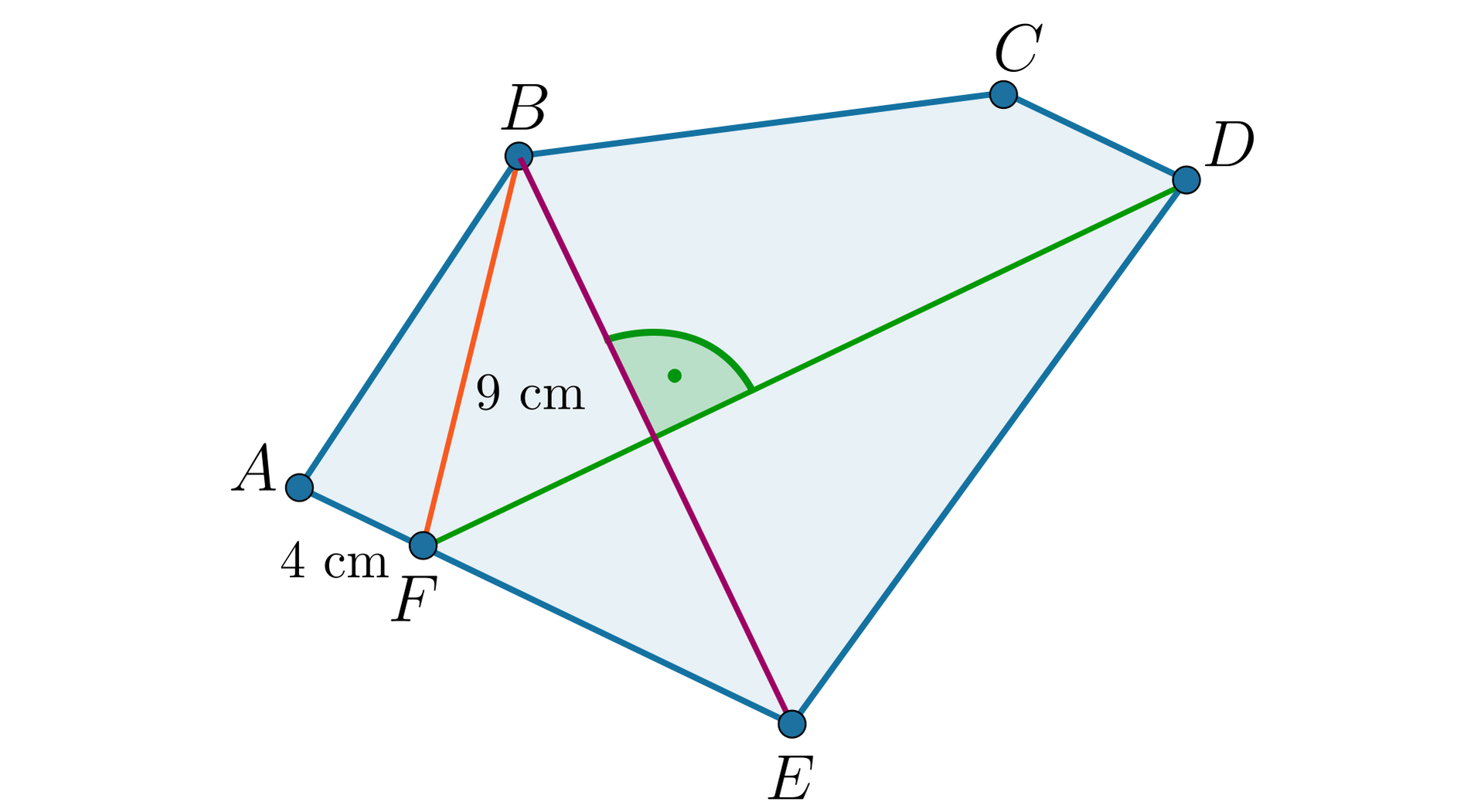
Obliczymy długość odcinka , jeżeli .
Punkt leży na symetralnej przekątnej zatem , wynika z tego, że .
Zatem
Ponieważ , zatem .
Animacja
Zapoznaj się z animacją. Poznasz ciekawe własności symetralnych boków trójkąta.

Film dostępny pod adresem /preview/resource/RV1jPYbNYutMv
Animacja nawiązująca do treści materiału
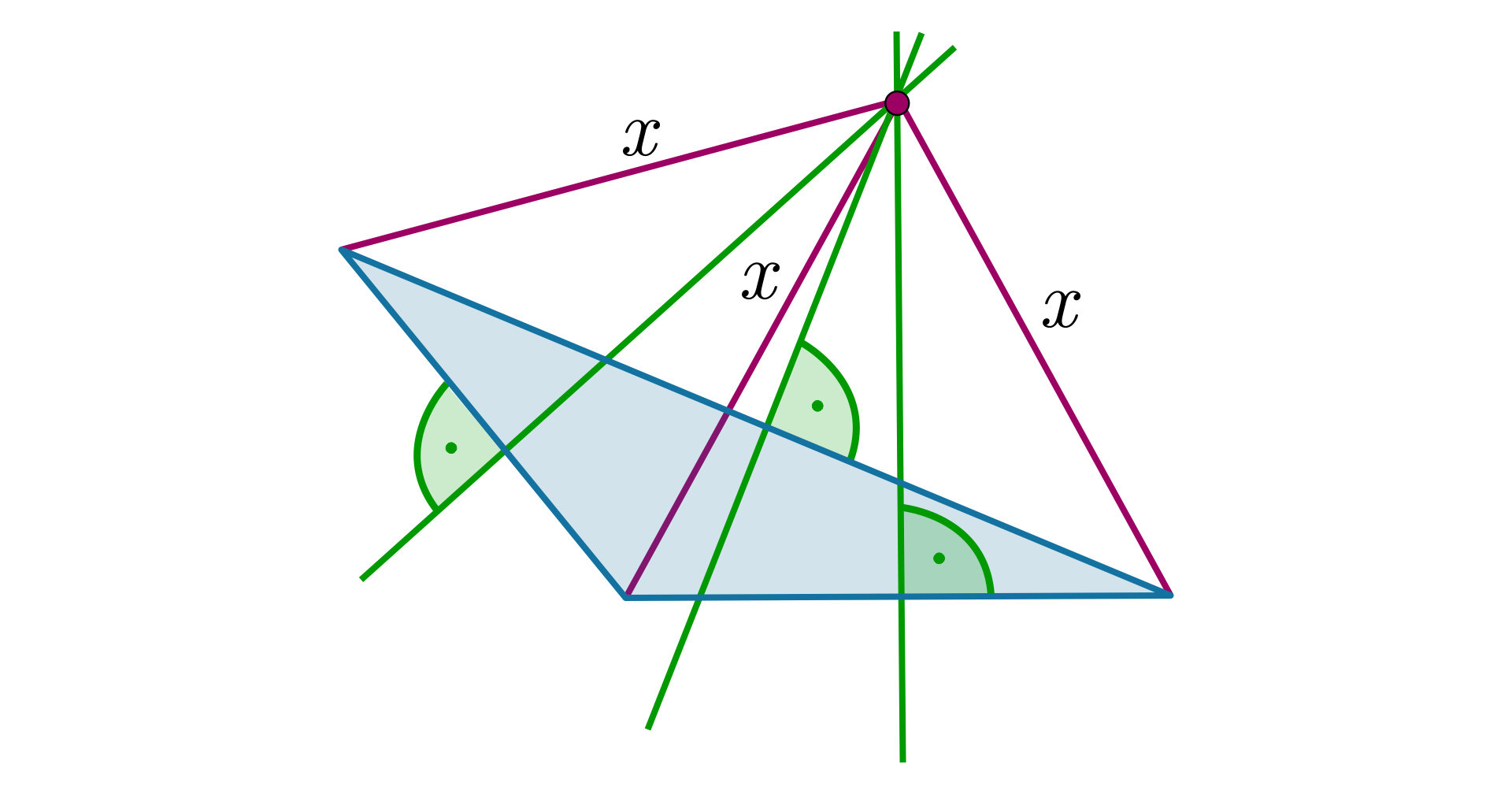
W trójkącie ostrokątnym symetralne boków i przecinają się pod kątem . Oblicz miarę kąta .
Narysuj trójkąt rozwartokątny i znajdź punkt równoodległy od każdego z wierzchołków tego trójkąta.
Pod jakim kątem ostrym przecinają się symetralne boków trójkąta równobocznego?
Na symetralnej odcinka zaznaczono punkt , a następnie poprowadzono symetralną odcinka .
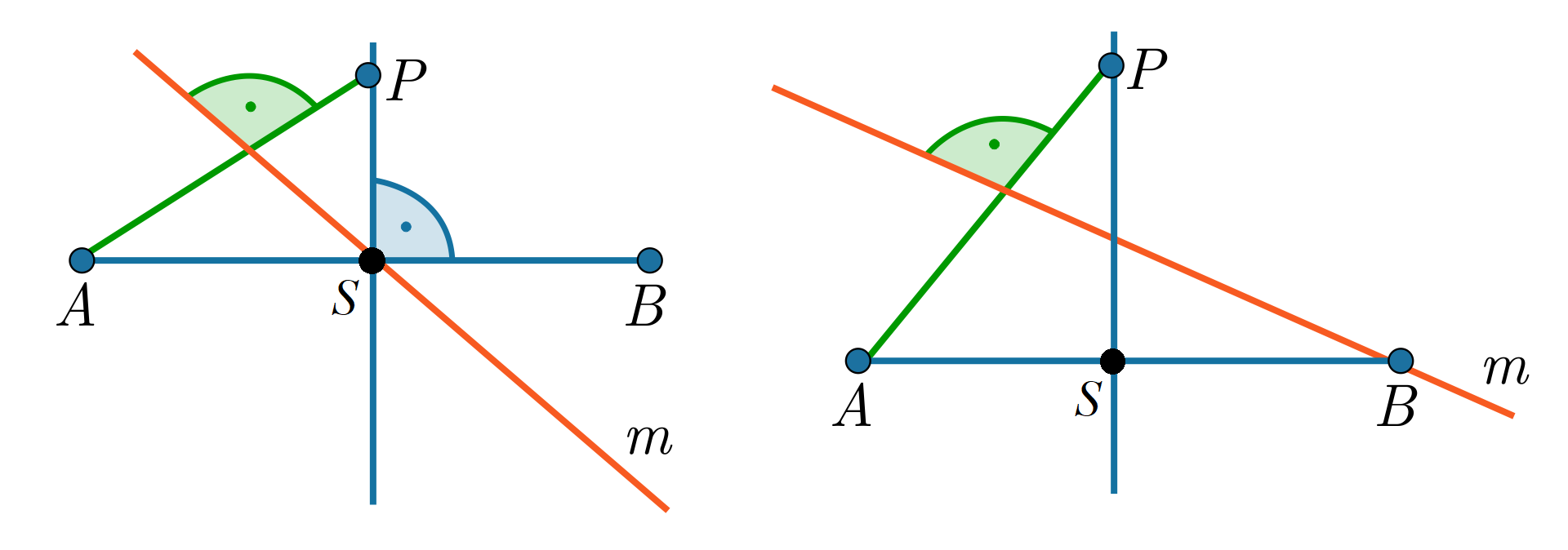
Na symetralnej odcinka zaznaczono punkt , a następnie poprowadzono symetralną odcinka . Prosta przetnie środek odcinka , gdy 1. , 2. , 3. , 4. .
Prosta przejdzie przez punkt , gdy 1. , 2. , 3. , 4. .
W trójkącie kąt ma miarę , kąt ma miarę . Symetralna boku przecina prostą pod kątem ostrym Tu uzupełnij
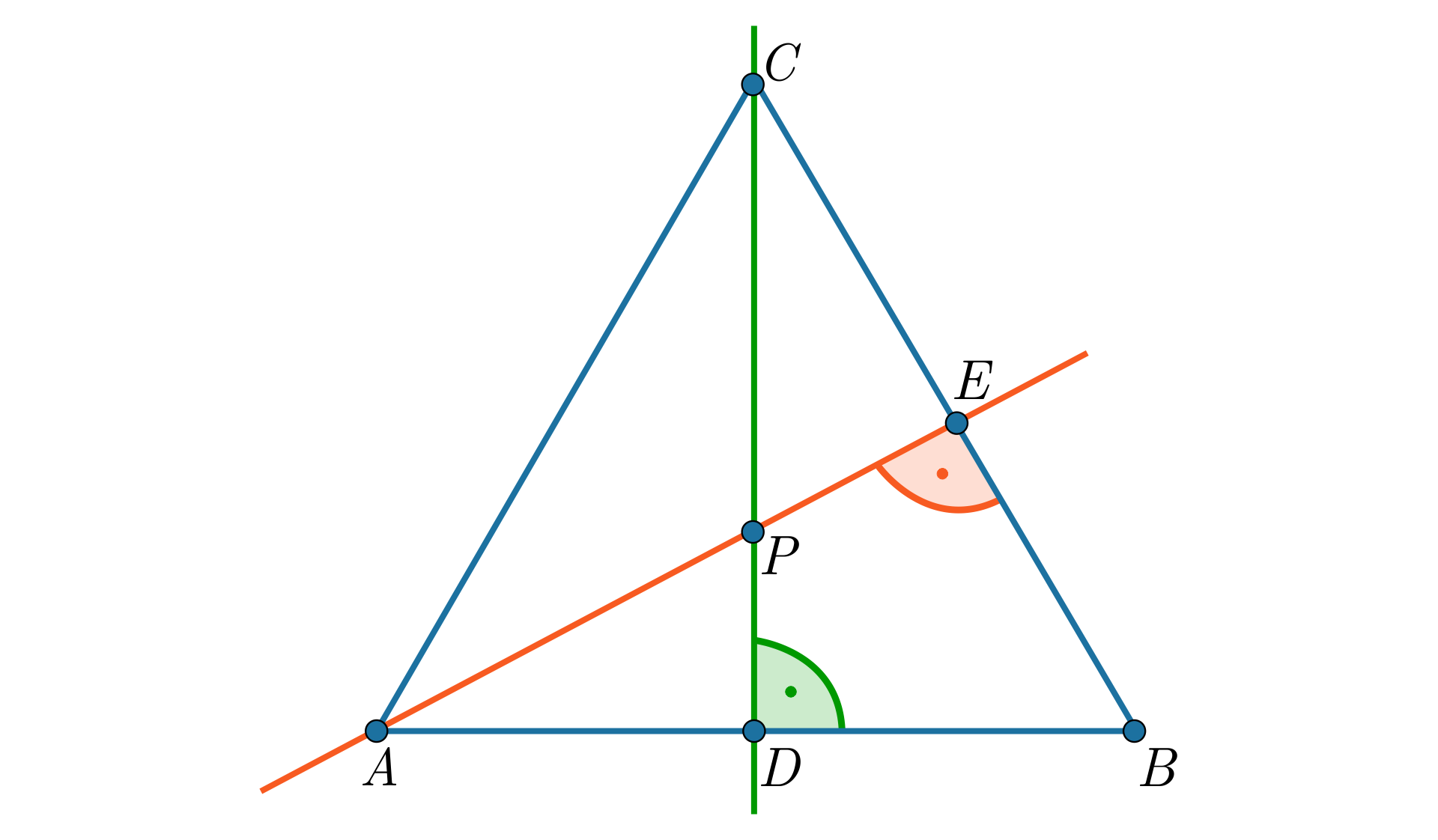
W trójkącie prosta jest symetralną boku , prosta jest symetralną boku . Proste te przecinają się w punkcie (patrz rysunek).
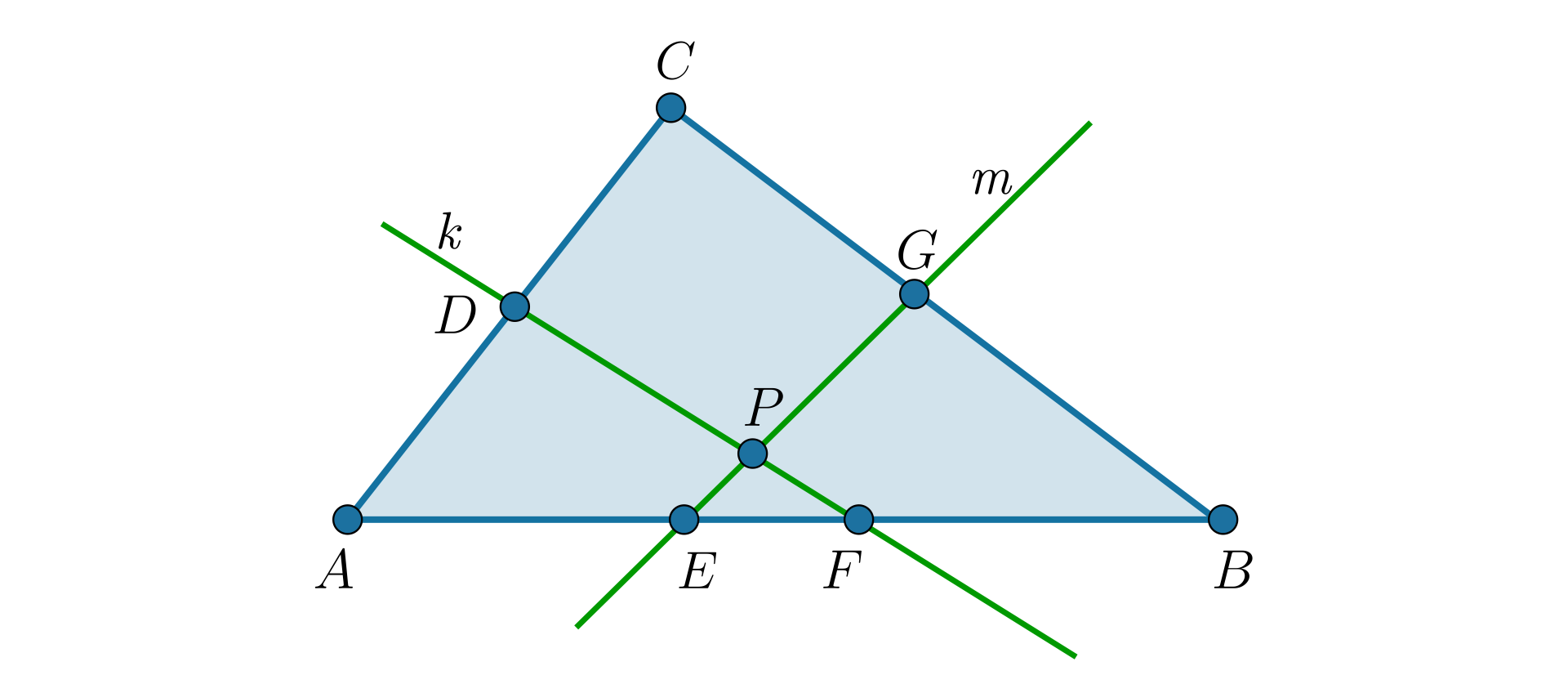
Na symetralnej odcinka obrano punkty i leżące po przeciwnych stronach tego odcinka.
Oblicz obwód czworokąta wiedząc, że i .
W pięciokącie każdy kąt ma miarę . Punkt jest punktem przecięcia symetralnych boków i . Wykaż, że proste i przecinają się pod kątem prostym.
Zaznacz poprawną odpowiedź.
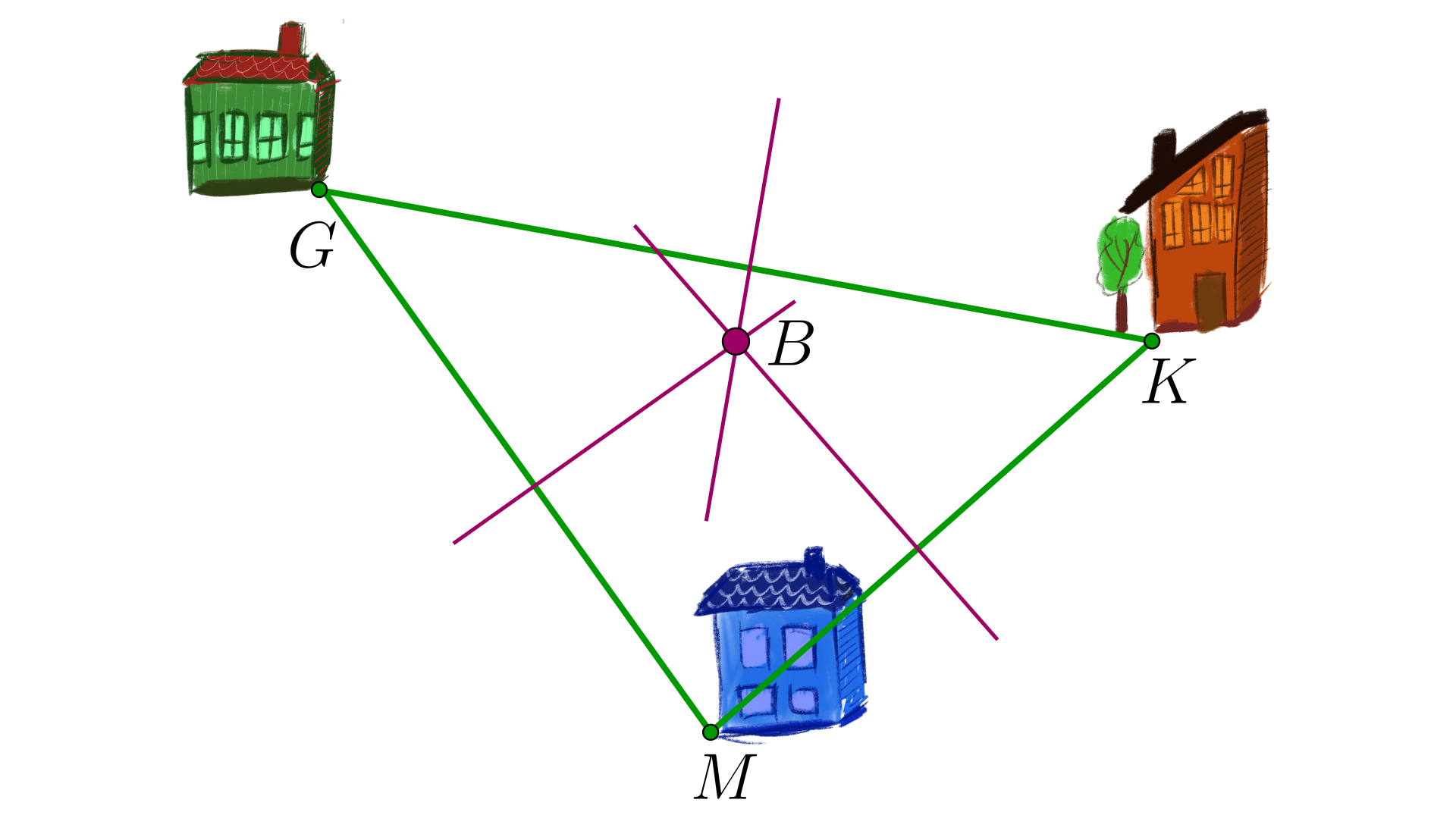
Skrzaty Gapcio, Klucznik i Miłek mieszkają w domach położonych tak, jak na rysunku. Znajdź punkt, w którym powinna stanąć budka z watą cukrową, aby każdy ze skrzatów miał do budki tak samo daleko.
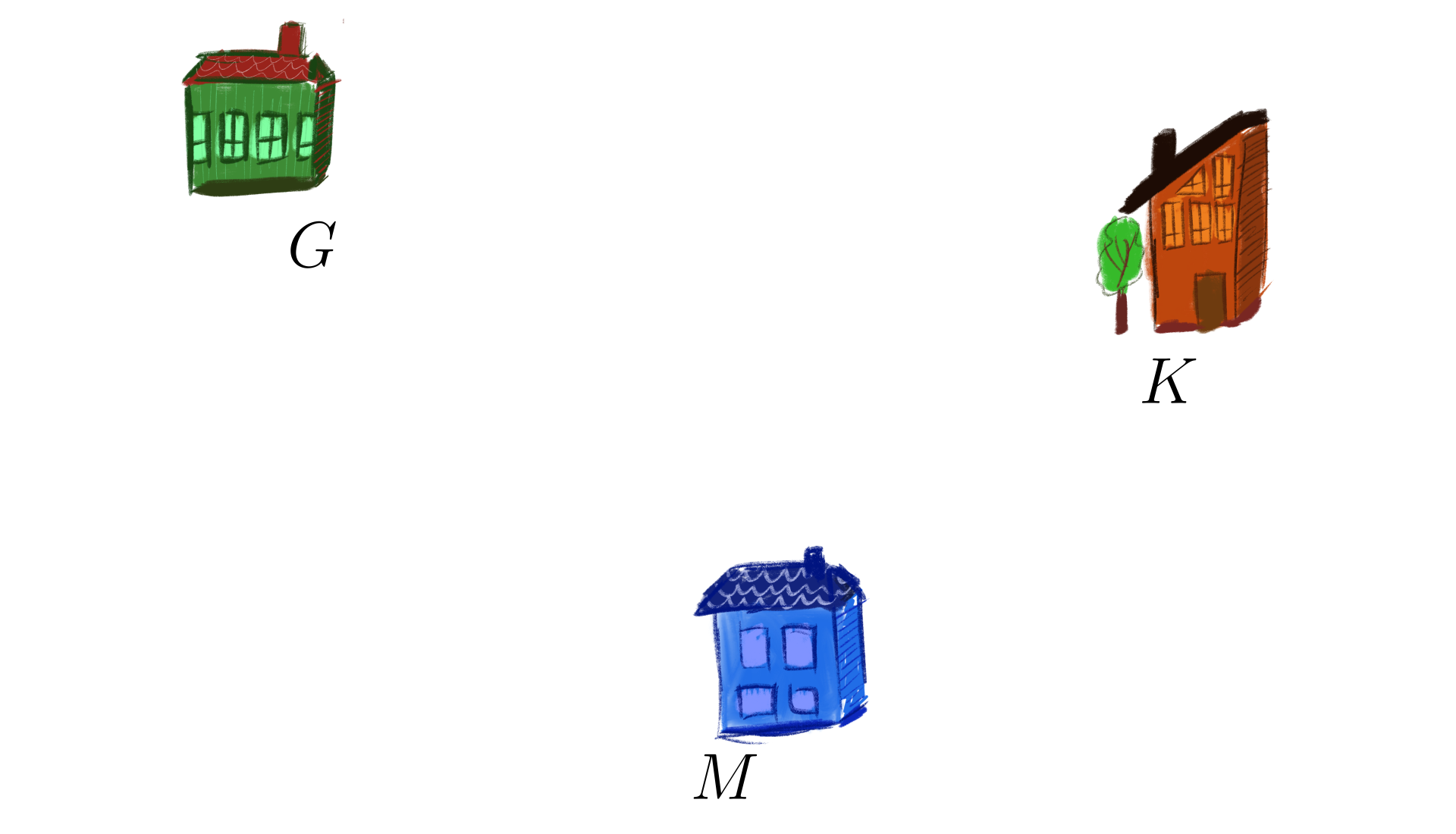
Skrzaty Gapcio, Klucznik i Miłek mieszkają w oddzielnych domach na jednym osiedlu. Chcieliby, aby budka z watą cukrową, powstająca na osiedlu, stała w takim miejscu, aby każdy z nich miał do budki tak samo daleko. Opisz czynności jakie należy wykonać, aby wyznaczyć punkt postawienia budki.
Prosta jest symetralną odcinka . Punkt jest środkiem tego odcinka. Zaznacz wszystkie zdania prawdziwe.
- Prosta jest prostopadła do odcinka .
- Prosta przechodzi przez środek odcinka .
- Punkty i leżą w tej samej odległości od punktu .
Narysuj dowolny odcinek i jego symetralną.
Opisz konstrukcję dowolnego odcinka i jego symetralnej.
- jest prostopadła do tego odcinka
- jest równoległa do tego odcinka
- przechodzi przez jeden z końców odcinka
- jest nachylona do odcinka pod kątem
Słownik
prosta prostopadła do tego odcinka i przechodząca przez jego środek.
Notatnik
Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.