2. Własności graniastosłupów

R9Bol1MChYzl01

Na fotografii przedstawiono wysoki podłużny wąski budynek znajdujący się na skrzyżowaniu ulic w Nowym Jorku.

Flatiron Building to budynek wybudowany w 1902 roku znajdujący się w Nowym Jorku. Jest jednym z pięciu najbardziej rozpoznawalnych symboli tego miasta. Nazwa Flatiron pochodzi od podobieństwa bryły budynku do starego żelazka na węgiel.

Sześcian i prostopadłościan to jedne z wielu brył, które udało Ci się do tej pory poznać. Bryły te to graniastosłupy proste, czyli takie graniastosłupy, których krawędzie boczne są prostopadłe do podstaw. Dzięki temu materiałowi dowiesz się, do jakiej grupy brył należy bryła, której realizację architektoniczną przedstawia budynek Flatiron Building.

Rodzaje graniastosłupów

Graniastosłupy są jednymi z częściej wykorzystywanych brył w życiu codziennym. Ich regularne kształty, w szczególności prostopadłościanu i graniastosłupów prawidłowych, są łatwe do odtworzenia i bardzo funkcjonalne, co stanowi inspirację dla architektów, konstruktorów i wytwórców. Trudno sobie wyobrazić jakiekolwiek miasto lub mieszkanie, w którym nie znajdowałyby się graniastosłupy: ich kształty znajdziemy w bryłach budowli, mebli, pudełek i wielu innych przedmiotach codziennego użytku.

RlS5Agww86Rb91

Animacja przedstawia różnego rodzaju figury przestrzenne.

Animacja przedstawia różnego rodzaju figury przestrzenne.

Film dostępny pod adresem /preview/resource/RlS5Agww86Rb9

Animacja przedstawia różnego rodzaju figury przestrzenne.

Prostopadłościan i sześcian są przykładami graniastosłupów prostych.

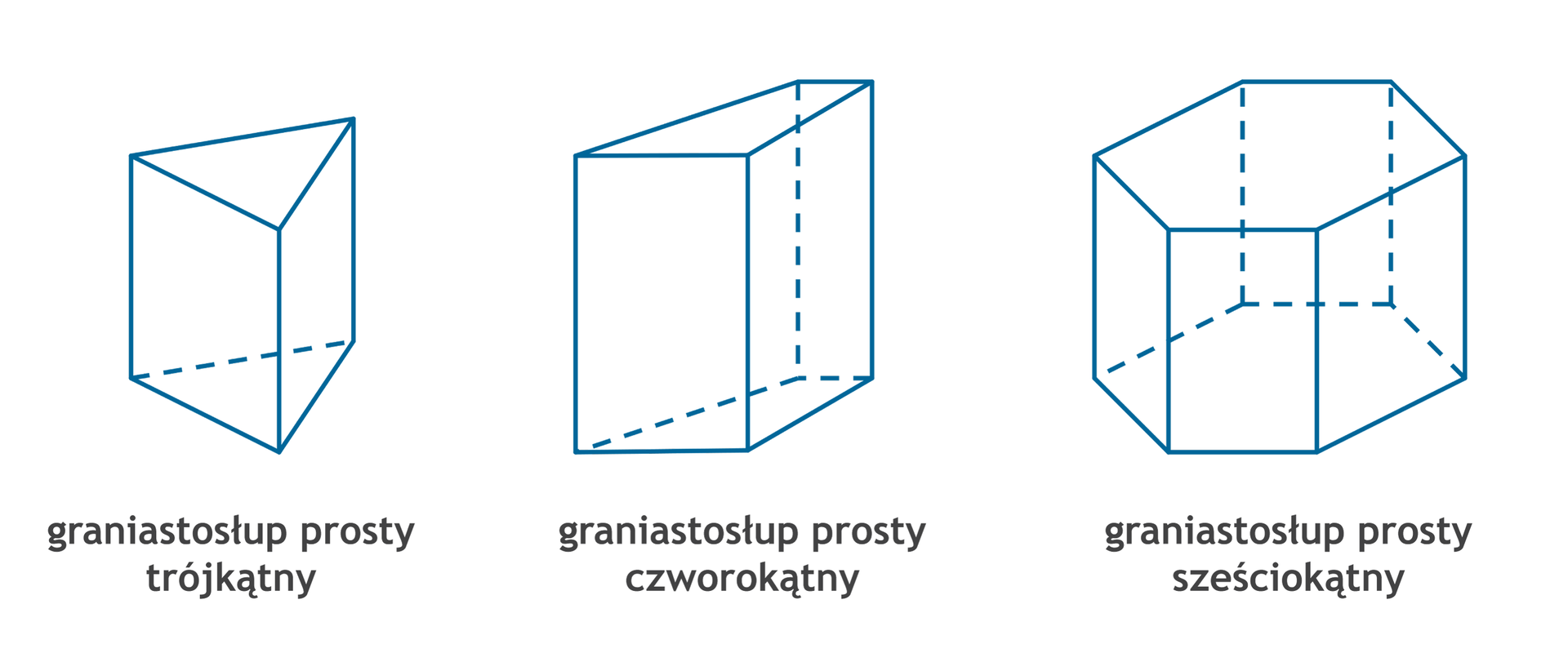
Graniastosłup prosty ma dwie podstawy w kształcie przystających wielokątów, leżące w równoległych płaszczyznach. Ściany boczne są prostokątami prostopadłymi do podstaw.

Nazwa graniastosłupa zależy od wielokąta, będącego jego podstawą.

Graniastosłup prosty

Definicja: Graniastosłup prosty

Graniastosłup prosty to taka figura przestrzenna, która ma:

• dwie podstawy będące jednakowymi wielokątami,

• ściany boczne będące prostokątami.

Nazwa graniastosłupa zależy od rodzaju wielokąta w podstawie.

RJTQFh5nNau7G1

Rysunek graniastosłupa prostego trójkątnego, graniastosłupa prostego czworokątnego i graniastosłupa prostego sześciokątnego.

RoqsbpwWYdxko1

Animacja pokazuje przykłady trzech figur przestrzennych, które są graniastosłupami o różnych podstawach.

Animacja pokazuje przykłady trzech figur przestrzennych, które są graniastosłupami o różnych podstawach.

Film dostępny pod adresem /preview/resource/RoqsbpwWYdxko

Animacja pokazuje przykłady trzech figur przestrzennych, które są graniastosłupami o różnych podstawach.

Jeśli podstawą graniastosłupa prostego jest wielokąt foremny (np. trójkąt równoboczny, kwadrat, pięciokąt foremny, sześciokąt foremny), wówczas graniastosłup taki nazywamy prawidłowym.

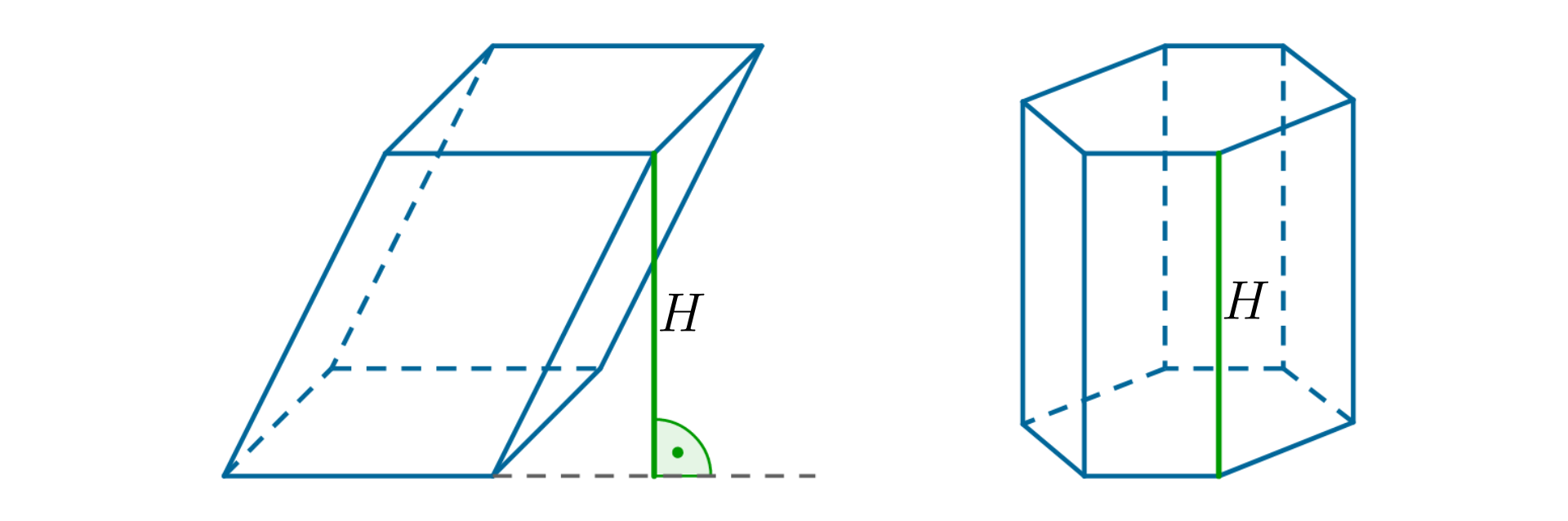
Inny rodzaj graniastosłupów to graniastosłupy pochyłe. Ich ściany boczne są równoległobokami. Najczęściej leżą w płaszczyznach, które nie są prostopadłe do podstaw.

Elementy graniastosłupa

Obejrzyj dokładnie model graniastosłupa.

RH3OjRQZf3PmT1

Rysunek graniastosłupa pięciokątnego z zaznaczonymi: podstawą górną, podstawą dolną, wierzchołkiem, ścianą boczną, krawędzią podstawy i krawędzią boczną.

Przykład 3

Podstawą graniastosłupa prawidłowego jest trójkąt o polu $25\sqrt{3}{\mathrm{c}\mathrm{m}}^2$. Wysokość graniastosłupa jest równa $12\mathrm{ cm}$. Obliczmy, ile centymetrów listewek potrzeba na wykonanie szkieletowego modelu tego graniastosłupa.

RZRkLHFW1ZysT1

Rysunek graniastosłupa prostego trójkątnego. Wszystkie krawędzie podstawy są równe a, wysokość bryły H.

Graniastosłup jest prawidłowy trójkątny, zatem jego podstawą jest trójkąt równoboczny.

Obliczamy długość $a$ krawędzi podstawy – korzystamy ze wzoru na pole trójkąta równobocznego.

$P=\frac{\sqrt{3}}{4}{a}^2=25\sqrt{3} {\mathrm{cm}}^2$

$a=\sqrt{100{\mathrm{cm}}^2}=10 \mathrm{cm}$.

Wszystkie krawędzie boczne graniastosłupa są równe i mają długość $12\mathrm{ cm}$.

Graniastosłup ma $6$ krawędzi podstaw i $3$ krawędzie boczne. Zatem potrzeba $6$ listewek długości $10\mathrm{ cm}$ i trzech długości $12\mathrm{ cm}$.

$6\cdot 10 \mathrm{cm}+3\cdot 12 \mathrm{cm}=60 \mathrm{cm}+36 \mathrm{cm}=96 \mathrm{cm}$.

Odpowiedź:

Na wykonanie modelu graniastosłupa potrzeba $96\mathrm{ cm}$ listewek.

Wysokością graniastosłupa nazywamy odległość między płaszczyznami zawierającymi jego podstawy. W przypadku graniastosłupów prostych, wysokość jest równa długości krawędzi bocznej.

RsgVkL4u3upGt1

Przekątna graniastosłupa to odcinek łączący dwa wierzchołki leżące w różnych podstawach i różnych ścianach bocznych.

R1ecvbV1bzcL51

Rysunek graniastosłupa prostego czworokątnego z poprowadzonymi odcinkami d oraz e łączącymi dwa wierzchołki leżące w różnych podstawach i różnych ścianach bocznych. Te odcinki są przekątnymi graniastosłupa.

Rysunek dwóch graniastosłupów z zaznaczonymi wysokościami równymi H. Pierwszy graniastosłup to graniastosłup pochyły. Jego wysokość jest opuszczona z wierzchołka górnej podstawy na płaszczyznę na której leży dolna podstawa pod kątem prostym. Drugi graniastosłup jest graniastosłupem prostym. Jego wysokość jest równa długości jego krawędzi bocznej.

Rysowanie graniastosłupów

Rysowanie graniastosłupa najlepiej rozpocząć od narysowania jego podstawy dolnej. Następnie rysujemy krawędzie boczne i łączymy ich końce, tworząc wielokąt będący podstawą górną. Niewidoczne krawędzie warto zaznaczyć liniami przerywanymi.

Przykład 4

Narysuj graniastosłup prosty, który w podstawie ma pięciokąt.

R1JvgbMkvRaLK1

Animacja przedstawia w jaki sposób możemy narysować graniastosłup prosty.

Animacja przedstawia w jaki sposób możemy narysować graniastosłup prosty.

Film dostępny pod adresem /preview/resource/R1JvgbMkvRaLK

Animacja przedstawia w jaki sposób możemy narysować graniastosłup prosty.

Ćwiczenie 2

Określ w każdym z graniastosłupów liczbę ścian bocznych, wierzchołków, krawędzi bocznych i podstaw.

Rxe3MKwtogtff1

Rysunek czterech graniastosłupów: A - graniastosłup o podstawie czworokąta, B - graniastosłup o podstawie trójkąta, C -graniastosłup o podstawie kwadratu, D - graniastosłup o podstawie prostokąta.

RabIgfQgkay8z

Uzupełnij komórki tabeli, wpisując odpowiednie wartości.

Uzupełnij komórki tabeli, wpisując odpowiednie wartości.

Ćwiczenie 3

Wskaż figurę, która nie może być podstawą graniastosłupa.

R1cexP42IbqnT1

Rysunki czterech figur: siedmiokąta, trapezu, sześciokąta i elipsy.

RiM00ycvM6Rv5

Zaznacz poprawną odpowiedź. Możliwe odpowiedzi: 1. $A$, 2. $B$, 3. $C$, 4. $D$

• A
• B
• C
• D

Ćwiczenie 3

Rimsqo3B9ICGh

Która z poniższych figur nie może być podstawą graniastosłupa? Zaznacz poprawną odpowiedź. Możliwe odpowiedzi: 1. trapez równoramienny, 2. elipsa, 3. sześciokąt, 4. siedmiokąt w kształcie strzałki

Ćwiczenie 11

R1e7v3g6utaGL1

Rysunek graniastosłupa o podstawie pięciokąta wklęsłego. Zaznaczono odcinek, który łączy dwa wierzchołki należące do różnych podstaw i różnych ścian bocznych.

RKsKPxYwXJPY5

Zaznacz prawidłowe zakończenie zdania. Zaznaczony odcinek w graniastosłupie, to Możliwe odpowiedzi: 1. przekątna ściany bocznej., 2. wysokość., 3. przekątna podstawy., 4. przekątna graniastosłupa.

• przekątna ściany bocznej
• wysokość
• przekątna podstawy
• przekątna graniastosłupa

R1Ygthzg0RknL

Uzupełnij poniższą lukę. Kliknij w nią, aby rozwinąć listę, a następnie wybierz poprawną odpowiedź. 1. Przekątną ściany bocznej, 2. Przekątną graniastosłupa, 3. Wysokością graniastosłupa, 4. Przekątną podstawy nazywamy odcinek łączący dwa wierzchołki graniastosłupa, leżące na różnych podstawach i na różnych ścianach bocznych.

Uzupełnij poniższą lukę. Kliknij w nią, aby rozwinąć listę, a następnie wybierz poprawną odpowiedź. 1. Przekątną ściany bocznej, 2. Przekątną graniastosłupa, 3. Wysokością graniastosłupa, 4. Przekątną podstawy nazywamy odcinek łączący dwa wierzchołki graniastosłupa, leżące na różnych podstawach i na różnych ścianach bocznych.

Notatnik

Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.