R1KArxESX7CXy
Rysunek przedstawia boisko. Na końcu boiska jest kosz do koszykówki. Napis: Wielokąty, koła i okręgi.

Wielokąty, koła i okręgi

Źródło: Santiago Pagnotta, dostępny w internecie: https://pexels.com/, domena publiczna.

10. Powtórzenie - geometria na płaszczyźnie

Zapoznaj się z poniższą grafiką, w której zaprezentowane są:

  • wzajemne położenie prostych,

  • kąty przyległe oraz ich miary,

  • kąty wierzchołkowe oraz ich miary,

  • definicja obwodu wielokąta,

  • suma miar kątów w trójkącie i czworokącie.

Będą one przydatne przy rozwiązywaniu ćwiczeń zawartych w tym materiale.

1
REqDsG5e70aRg
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Informacje zawarte na mapie myśli:

  1. Suma miar kątów wewnętrznych w trójkącie wynosi 180°.

  2. Suma miar kątów wewnętrznych w czworokącie wynosi 360°.

  3. Obwód to suma długości wszystkich boków wielokąta.

  4. Kąty przyległe sumują się do 180°.

  5. Kąty wierzchołkowe w parze mają równe miary. Przykładowo, kąty wierzchołkowe występują w momencie przecięcią się dwóch prostych. Występują wtedy dwie pary kątów wierzchołkowych, których miary sumują się do 360°.

  6. Dwie proste nie mające punktów wspólnych, to proste równoległe.

  7. Dwie proste przecinające się pod kątem prostym, to proste prostopadłe.

R1B5ywOzLzKP5
Ćwiczenie 1
Na którym rysunku przedstawiono prostą AB?

  • 60943
  • 60944
  • 60945
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
REdogp0jTLuQK
Ćwiczenie 1
Połącz pojęcie z definicją. prosta Możliwe odpowiedzi: 1. część prostej ograniczona z jednej strony punktem tej prostej, a z drugiej strony nieograniczona., 2. linia prosta nieograniczona z obu stron, 3. część prostej zawarta pomiędzy dwoma punktami tej prostej, z tymi punktami włącznie. półprosta Możliwe odpowiedzi: 1. część prostej ograniczona z jednej strony punktem tej prostej, a z drugiej strony nieograniczona., 2. linia prosta nieograniczona z obu stron, 3. część prostej zawarta pomiędzy dwoma punktami tej prostej, z tymi punktami włącznie. odcinek Możliwe odpowiedzi: 1. część prostej ograniczona z jednej strony punktem tej prostej, a z drugiej strony nieograniczona., 2. linia prosta nieograniczona z obu stron, 3. część prostej zawarta pomiędzy dwoma punktami tej prostej, z tymi punktami włącznie.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 2

Na prostej k zaznaczono punkty C, D, E.

RK9k8jY1WOIxr1
Na rysunku przedstawiona jest prosta k przechodząca przez trzy punkty C, D i E.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RckACf4Bkqbze
Ile odcinków powstało? Zaznacz poprawną odpowiedź. Możliwe odpowiedzi: 1. 3, 2. 4, 3. 2, 4. 1
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 3

Zapoznaj się z poniższym rysunkiem dwóch takich samych prostokątów.

RGEZ0QTL54fEQ1
Rysunek dwóch prostokątów. W pierwszym prostokącie dwa sąsiadujące boki oznaczone są jednym kolorem. W drugim prostokącie boki leżące naprzeciw siebie oznaczone są jednym kolorem.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1biHOQ1H0jy9
Na którym rysunku zaznaczono tym samym kolorem prostopadłe boki prostokąta? Zaznacz poprawną odpowiedź. Możliwe odpowiedzi: 1. Na pierwszym., 2. Na drugim., 3. Na obu., 4. Na żadnym.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 4

Zapoznaj się z poniższym planem pewnego miasta.

RODFALIdHQrVp1
Fragment planu miasta.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1aC4CnP3dhpm
Odpowiedz na podstawie rysunku. Uzupełnij poniższe zdania, wpisując w luki odpowiednie nazwy ulic. Nazwa ulicy równoległej do ulicy Kilińskiego to ulica Tu uzupełnij.Nazwa ulicy równoległej do ulicy Północnej to ulica Tu uzupełnij i ulica Tu uzupełnij.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 4

Podaj nazwy ulic, które są prostopadłe, a które są równoległe do ulicy z Twojego adresu zamieszkania.

Ćwiczenie 5

Zapoznaj się z poniższą grafiką, na której przedstawione są różne figury.

RgEuWe5YjsVDR1
Rysunek dziesięciu różnych figur.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RSMKkzbpxAVbc
Wypisz litery znajdujące się na rysunkach tych figur, które są kwadratami i prostokątami. Uzupełnij zdania, przeciągając w luki odpowiednie litery w kolejności alfabetycznej lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. Kwadratami są figury Tu uzupełnij i Tu uzupełnij.Prostokątami są figury Tu uzupełnij, Tu uzupełnij, Tu uzupełnij i Tu uzupełnij.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 5

Podaj przedmioty w życiu codziennym których kształt jest:

  1. kwadratem

  2. prostokątem

Ćwiczenie 6

  1. Narysuj wszystkie przekątne prostokąta RAMI.

R1JUfueXbWY5R
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

  1. Wymień wszystkie przekątne prostokąta RAMI.

RaKAymq8WVUS71
Rysunek prostokąta R A M I. Boki A R i M I to para boków równoległych, które są dłuższe od drugiej pary boków równoległych - R I oraz AM.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RamYrCV1Tzdh3
Ile przekątnych ma ten prostokąt? Uzupełnij odpowiedź, wpisując w lukę odpowiednią liczbę. Odpowiedź: Ten prostokąt ma Tu uzupełnij przekątne.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

  1. Narysuj wszystkie przekątne kwadratu FOKA.

R7U2yJnRC6Yyc
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

  1. Wymień wszystkie przekątne kwadratu FOKA. Pod jakim kątem przecinają się te przekątne?

RAzewj6OMZaw91
Rysunek kwadratu F O K A. Boki A K, K O, O F i F A są równej długości.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RPD7nVoOWdF92
Pod jakim kątem przecinają się te przekątne? Uzupełnij odpowiedź, wpisując w lukę odpowiednią liczbę. Odpowiedź: Przekątne w tym kwadracie przecinają się pod kątem Tu uzupełnij°.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 7

Odpowiedz na poniższe pytania. Zaznacz prawidłowe odpowiedzi.

Odpowiedz na poniższe pytania. Zaznacz prawidłowe odpowiedzi.

R1UScDgp6ZNK51
Rysunek wielokąta, który ma 6 boków.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RjRBCfnUAteaP
Ile wierzchołków ma przedstawiony na rysunku wielokąt? Możliwe odpowiedzi: 1. 6, 2. 4, 3. 5, 4. 3
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R16JTz4ikyZBY
2. Ile kątów ma wielokąt ABCDEFGH? Zaznacz poprawną odpowiedź. Możliwe odpowiedzi: 1. 8, 2. 6, 3. 10, 4. 7
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1OEjrvEizxc21
Ćwiczenie 8
Uzupełnij poniższe zdania, wpisując w luki odpowiednie liczby. Łamana, której odcinki mają następujące długości: 3 cm, 5 cm, 7 cm, ma łączną długość Tu uzupełnij cm.Łamana, której odcinki mają następujące długości: 6 cm 2 mm, 5 cm 7 mm, 8 cm 7 mm, ma łączną długość Tu uzupełnij cm Tu uzupełnij mm.

Uzupełnij.

a) Łamana, której odcinki mają następujące długości: 3 cm, 5 cm, 7 cm, ma łączną długość ............ cm.
b) Łamana, której odcinki mają następujące długości: 6 cm 2 mm, 5 cm 7 mm, 8 cm 7 mm, ma łączną długość ............ cm ............ mm.

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RoiedlPXK1yJE1
Ćwiczenie 9
Uzupełnij zdania, przeciągając w luki odpowiednie liczby i słowa lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. Kąt półpełny ma 1. półpełny, 2. rozwarty, 3. 90°, 4. 270°, 5. prosty, 6. 180°, 7. 360°, 8. wklęsły, 9. pełny, 10. ostry.Wskazówka minutowa zegara pomiędzy 11:00 a 11:26 zakreśla kąt 1. półpełny, 2. rozwarty, 3. 90°, 4. 270°, 5. prosty, 6. 180°, 7. 360°, 8. wklęsły, 9. pełny, 10. ostry.

Przeciągnij i upuść.

wklęsły, 90∘, rozwarty, półpełny, prosty, 360∘, 270∘, pełny, 180∘, ostry

a) Kąt półpełny ma .......................
b) Wskazówka minutowa zegara pomiędzy 11:00 a 11:26 zakreśla kąt .......................

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R9XaY9DIZbVse1
Ćwiczenie 10
Uzupełnij poniższe zdania, wpisując w luki odpowiednie liczby. Średnica koła ma długość 2 cm, więc promień tego koła ma Tu uzupełnij cm.Promień okręgu ma długość 4 cm 6 mm, więc jego średnica ma długość Tu uzupełnij cm Tu uzupełnij mm.

Uzupełnij.

a) Średnica koła ma długość 2 cm, więc promień tego koła ma ............ cm.
b) Promień okręgu ma długość 4 cm 6 mm, więc jego średnica ma długość ............ cm ............ mm.

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1QVk8RDomkGd
Ćwiczenie 11
Uzupełnij poniższe zdania, wpisując w luki odpowiednie liczby. Obwód kwadratu o boku długości 3 cm wynosi Tu uzupełnij cm.Długość boku kwadratu o obwodzie równym 60 cm wynosi Tu uzupełnij cm.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1CPHgMBenkIZ1
Ćwiczenie 12
Uzupełnij poniższe zdania, wpisując w luki odpowiednie liczby. Obwód prostokąta o bokach długości 3 cm i 6 cm wynosi Tu uzupełnij cm.Obwód prostokąta, którego jeden bok ma długość 12 cm, a drugi bok jest od niego trzy razy krótszy wynosi Tu uzupełnij cm.

Uzupełnij.

a) Obwód prostokąta o bokach długości 3 cm i 6 cm wynosi ............ cm.
b) Obwód prostokąta, którego jeden bok ma długość 12 cm, a drugi bok jest od niego trzy razy krótszy wynosi ............ cm.

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RgHt4Cq412Nuu1
Ćwiczenie 13
Ołówek ma długość 12 cm. Na podstawie tej informacji uzupełnij poniższe zdania, przeciągając w luki odpowiednie liczby i skale lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. Ołówek narysowany w skali 2:1 ma długość 1. 1:6, 2. 24, 3. 25, 4. 1:5, 5. 18, 6. 1:4, 7. 26, 8. 1:3, 9. 1:8, 10. 22, 11. 20 cm.Na rysunku ołówek ma długość 2 cm. Rysunek ten wykonano w skali 1. 1:6, 2. 24, 3. 25, 4. 1:5, 5. 18, 6. 1:4, 7. 26, 8. 1:3, 9. 1:8, 10. 22, 11. 20.

Ołówek ma długość 12 cm.

18, 1:3, 1:8, 1:4, 25, 24, 20, 1:5, 1:6, 22, 26

a) Ołówek narysowany w skali 2 : 1 ma długość ............ cm.
b) Na rysunku ołówek ma długość 2 cm. Rysunek ten wykonano w skali .............

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1Cv9uT8QPh5q1
Ćwiczenie 14
Prostokątna działka na planie w skali 1:100 ma wymiary 11 cm 5 mm i 8 cm. Uzupełnij poniższe zdania, wpisując w luki odpowiednie liczby. W rzeczywistości krótszy bok tej działki ma długość Tu uzupełnij m. W rzeczywistości dłuższy bok tej działki ma długość Tu uzupełnij m Tu uzupełnij cm.

Prostokątna działka na planie w skali 1 : 100 ma wymiary 11 cm 5 mm i 8 cm.

a) Rzeczywista szerokość tej działki wynosi ............ m.
b) Rzeczywiste wymiary działki wynoszą ............ m ............ cm   i   ............ m.

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R5m7NYxbHNWUb
Ćwiczenie 15
Prostokąt o wymiarach 4 cm i 2 cm narysowano w skali 1:2 i 3:1. Uzupełnij poniższe zdania, wpisując w luki odpowiednie liczby. Obwód prostokąta narysowanego w skali 1:2 wynosi Tu uzupełnij cm. Obwód prostokąta narysowanego w skali 3:1 wynosi Tu uzupełnij cm.Różnica między obwodem prostokąta narysowanego w skali 3:1 i obwodem prostokątna narysowanego w skali 1:2 wynosi Tu uzupełnij cm.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1LL9XCxPiM55
Ćwiczenie 16
Odległość między dwiema miejscowościami na mapie w skali 1:1000000 jest równa 5 cm. Oblicz, jaka jest rzeczywista odległość między tymi miejscowościami. Wynik podaj w kilometrach. Uzupełnij odpowiedź, wpisując w lukę odpowiednią liczbę. Odpowiedź: Odległość ta wynosi Tu uzupełnij km.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RKBpK4xgdTR68
Ćwiczenie 17
Łamana otwarta FGHJ ma trzy boki. Długość odcinka FG wynosi 6 cm, długość odcinka GH jest dwa razy krótsza od długości odcinka FG, zaś długość łamanej wynosi 20 cm. Oblicz długość odcinka HJ. Uzupełnij poniższe zdanie, przeciągając w lukę odpowiednią liczbę lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. Długość odcinka HJ wynosi 1. 12, 2. 11, 3. 10, 4. 13 cm.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 18

Narysuj dwa okręgi o środku w punkcie P i promieniach odpowiednio 2 cm i 6 cm.

RRwLbIvkH3BZt
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Dane są dwa okręgi o środku w punkcie P i promieniach odpowiednio 2 cm i 6 cm.

R1GXgK0Ky4IqK
Uzupełnij poniższe zdanie, wpisując w lukę odpowiednią liczbę. Średnica większego okręgu jest Tu uzupełnij razy dłuższa od promienia mniejszego okręgu.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 19

Czworokąt FOKA jest kwadratem.

Przyjrzyj się rysunkowi i odpowiedz na pytania.

Rgi15fwQ4MDZG1
Rysunek kwadratu F O K A. Poprowadzone przekątne przecinają się w punkcie P.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

  1. Ile par odcinków równoległych jest na rysunku?

  2. Ile par odcinków prostopadłych jest na rysunku?

Punkt P jest miejscem przecięcia przekątnych kwadratu.

  1. Ile par odcinków równoległych jest w tym kwadracie?

  2. Ile par odcinków prostopadłych jest w tym kwadracie?

R1F2IITPtZvLm
Ad 1. Par odcinków równoległych jest 1. 6, 2. 11, 3. 7, 4. 5, 5. 9, 6. 4.
Ad 2. Par odcinków prostopadłych jest 1. 6, 2. 11, 3. 7, 4. 5, 5. 9, 6. 4.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 20

Na rysunku prosta p jest równoległa do prostej GT.

R1HPBsxoC1rfm1
Rysunek dwóch prostych równoległych p i TG, które są przecięte trzecią prostą k. Do prostej k z punktu T poprowadzone trzy różne odcinki.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R11kqdV5g3hQl
Odczytaj dane z rysunku i podaj odległość
1. punkt T od prostej k.
2. prostej GT od prostej p. Ad 1. Tu uzupełnij Ad 2. Tu uzupełnij
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RJD0oRyOyGFrO
Ćwiczenie 20
Pogrupuj elementy z życia codziennego, które są prostymi równoległymi lub prostopadłymi. proste równoległe Możliwe odpowiedzi: 1. fragment torów kolejowych, 2. przewody wysokiego napięcie, 3. litera X, 4. pasy na przejściu dla pieszych, 5. znak dodawania, 6. róg prostokątne stołu proste prostopadłe Możliwe odpowiedzi: 1. fragment torów kolejowych, 2. przewody wysokiego napięcie, 3. litera X, 4. pasy na przejściu dla pieszych, 5. znak dodawania, 6. róg prostokątne stołu
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R139vuZcBs4Dm
Ćwiczenie 21
Rozstrzygnij, czy zdanie jest prawdziwe, czy fałszywe. Możliwe odpowiedzi: 1. Kąt o 20° większy od kąta półpełnego to kąt rozwarty., 2. Kąt trzykrotnie większy od kąta o mierze 30° to kąt prosty.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 22

Oblicz miarę kąta α.

Re5x2QDrMn6Px1
Rysunek trójkąta prostokątnego o kątach ostrych alfa i 28 stopni.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Dany jest trójkąt prostokątny o kątach ostrych równych α oraz 28°. Oblicz miarę kąta α.

RLilCPmYFrxQS
Wpisz w wyznaczone miejsce odpowiednie wyrażenie. Kąt α= Tu uzupełnij°
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 23

Oblicz miarę kąta α, jeżeli

RfEjG1TrXQCMt1
Grafika statyczna
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

  1. dane są dwa kąty przyległe, z których jeden ma miarę 110°, a drugi α,

  2. dany jest kąt prosty i kąty o miarach odpowiednio 49° oraz α, które dopełniają się do prostej.

R1NyVB12dJUT5
Wpisz w wyznaczone miejsce odpowiednie wyrażenie. a. α=Tu uzupełnij° b. α=Tu uzupełnij°
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 24

Podaj miary kątów oznaczonych literami.

RRNszQGqwOoag1
Rysunki prostych z zaznaczonymi między nimi kątami. Na pierwszym rysunku, miedzy dwoma prostymi, zaznaczone kąty wierzchołkowe alfa i 57 stopni. Na drugim rysunku, między trzema prostymi, zaznaczone kąty 45 stopni, beta, 86 stopni i gamma. Kąty 45 stopni, beta i 86 stopni tworzą kąt półpełny. Kąt 45 stopni jest kątem wierzchołkowym do kąta gamma.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

  1. Dane są kąty wierzchołkowe, w których naprzeciwko kąta o mierze α leży kąt o mierze 57°.

  2. Pęk trzech prostych przecinających się w jednym punkcie tworzy sześć kątów dopełniających się do kąta pełnego. Cztery pierwsze kąty mają kolejno miarę 45 ∘ , β, 86 ° oraz γ.

RtP7ITNcndMPb
Wpisz w wyznaczone miejsce odpowiednie wyrażenie. a) α= Tu uzupełnij°. b) β= Tu uzupełnij°, γ= Tu uzupełnij°.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 25

W trójkącie równoramiennym kąt przy podstawie ma miarę 50°. Oblicz miarę kąta między ramionami tego trójkąta.

R2v5oBHkrC6c0
Wpisz w wyznaczone miejsce odpowiednie wyrażenie. Miarą kąta między ramionami tego trójkąt jest Tu uzupełnij°.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 26

Oblicz miarę kąta α równoległoboku.

RRBYp6BiU2W011
Rysunek równoległoboku. Zaznaczone kąty alfa i 40 stopni leżące przy jednym boku.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Oblicz miarę kąta α równoległoboku, którego kąt ostry ma miarę 40°.

Ro7EHG14iWLMK
Wpisz w wyznaczone miejsce odpowiednie wyrażenie. Miarą kąta α równoległoboku jest Tu uzupełnij°.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 27

Rozstrzygnij, czy zdanie jest prawdziwe, czy fałszywe.
Zaznacz zdanie prawdziwe.

R1AZjXhH4AJDZ1
Rysunek równoległoboku A P O R, którego przekątne przecinają się w punkcie S. Kąt S P O ma miarę 20 stopni.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Przekątne równoległoboku PORA przecinają się w punkcie S, SO=3 oraz PS=4 oraz ∢SPO=20°.

Rozstrzygnij, czy zdanie jest prawdziwe, czy fałszywe. Zaznacz zdanie prawdziwe.

RkJM3wTKB6JDC
Możliwe odpowiedzi: 1. W każdym rombie przekątne są prostopadłe., 2. Suma kątów czworokąta wynosi 180°., 3. Miara kąta POR wynosi 160°., 4. Suma długości przekątnych tego równoległoboku wynosi 8.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 28

W trapezie prostokątnym kąt ostry przy podstawie ma miarę 43°. Oblicz miary pozostałych kątów tego trapezu.

R1BiLvALzwCAI
Przeciągnij i upuść poprawne wyrażenie we właściwe miejsce. Miary pozostałych kątów tego trapezu: 1. 80°, 2. 137°, 3. 90°, 4. 80°, 5. 138°, 6. 147°, 7. 90°, 1. 80°, 2. 137°, 3. 90°, 4. 80°, 5. 138°, 6. 147°, 7. 90°, 1. 80°, 2. 137°, 3. 90°, 4. 80°, 5. 138°, 6. 147°, 7. 90°.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 29

Oblicz obwód trapezu przedstawionego na rysunku.

RfHUtGPA3lCHq1
Rysunek trapezu równoramiennego o ramionach długości 2 m i podstawach równych 6 m i 4 m.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Oblicz obwód trapezu równoramiennego, którego dłuższa podstawa ma długość 6 m. Krótsza podstawa jest krótsza o 2 m, a długość jednego ramienia trapezu jest równa połowie długości krótszej podstawy.

R17kxoaMSiORT
Wpisz w wyznaczone miejsce odpowiednie wyrażenie. Obwód trapezu przedstawionego na rysunku wynosi Tu uzupełnijm.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 30

Oblicz obwód narysowanego czworokąta.

RtFCVQmwJ0soI1
Rysunek dwóch czworokątów. Na pierwszym rysunku równoległobok o bokach 6 cm i 12 cm. Na drugim rysunku romb o boku 5 cm.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Oblicz obwód:

  1. równoległoboku o wymiarach 6 cm×12 cm,

  2. rombu o krawędzi równej 5 cm.

RngHGHfDKGB6t
Przeciągnij i upuść poprawne wyrażenie we właściwe miejsce. a) 1. 25 cm, 2. 20 cm, 3. 39 cm, 4. 36 cm, 5. 17 cm
b) 1. 25 cm, 2. 20 cm, 3. 39 cm, 4. 36 cm, 5. 17 cm
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 31

Policz, ile jest na poniższym rysunku

  1. równoległoboków,

  2. trapezów?

R12AmHaNFt7A11
Rysunek jedenastu różnych figur.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RgG4vGcaVD3gc
Zaznacz prawidłowe odpowiedzi. Możliwe odpowiedzi: 1. równoległoboków 5, 2. trapezów 8, 3. równoległoboków 6, 4. równoległoboków 9, 5. trapezów 7, 6. trapezów 4
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Rwh30niunZkoQ
Zaznacz wszystkie prawdziwe zadania. Możliwe odpowiedzi: 1. Każdy prostokąt jest równoległobokiem., 2. Każdy trapez jest równoległobokiem., 3. Każdy kwadrat jest rombem., 4. Równoległobok i romb to jest określenie tej samej figury.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 32

  1. Oblicz długość boku kwadratu o obwodzie 48 cm.

  2. Babcia obszyła tasiemką brzeg prostokątnej serwety o wymiarach 80 cm x 140 cm. Ile co najmniej centymetrów tasiemki zużyła?

RepJg4VgVyxmy
Przeciągnij i upuść poprawne wyrażenie we właściwe miejsce. Ad 1. 1. 12 cm, 2. 360 cm, 3. 14 cm, 4. 28 cm, 5. 440 cm, 6. 360 cm.
Ad 2. 1. 12 cm, 2. 360 cm, 3. 14 cm, 4. 28 cm, 5. 440 cm, 6. 360 cm.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R5GgFSImnh79a
Ćwiczenie 33
Obwód trapezu równoramiennego wynosi 30 dm, ramię ma długość 5 dm, a podstawa górna 14 dm. Oblicz długość dolnej podstawy tego trapezu.
Zaznacz prawidłową odpowiedź. Możliwe odpowiedzi: 1. 6 dm, 2. 12 dm, 3. 8 dm, 4. 9 dm
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 34
RUJCcEDmn1w8d
1. Oblicz obwód trójkąta równoramiennego, którego ramię o długości 6 cm jest dłuższe od podstawy o 3 cm.
2. Obwód trójkąta równoramiennego wynosi 36 cm, podstawa ma długość 16 cm. Jaką długość mają ramiona tego trójkąta?
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 35
RFflYxe0A9YXd
1. Oblicz obwód równoległoboku, w którym jeden bok ma długość 8 cm, a drugi jest od niego o 5 cm krótszy.
2. Równoległobok i romb mają takie same obwody. Bok rombu ma długość 7 cm, a jeden z boków równoległoboku 5 cm.
Oblicz długość drugiego boku równoległoboku. Wpisz w wyznaczone miejsce odpowiednie wyrażenie.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1HjFKdD7Evxt
Ćwiczenie 36
Poniżej przedstawiono wymiary pewnych prostokątów. Które z tych prostokątów mają obwód równy 30 cm?
Zaznacz wszystkie prawidłowe odpowiedzi. Możliwe odpowiedzi: 1. 1 cm × 14 cm, 2. 2 cm × 13 cm, 3. 3 cm × 12 cm, 4. 4 cm × 11 cm, 5. 5 cm × 10 cm, 6. 6 cm × 9 cm, 7. 7 cm × 8 cm, 8. 4 cm × 12 cm, 9. 3 cm × 11 cm, 10. 5 cm × 11 cm
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 37
R1EP0R1uGozNa
Jak zmieni się obwód równoległoboku o wymiarach a i b, jeżeli
1. jeden z wymiarów zwiększy się o 5
2. jeden z wymiarów zwiększy się o 4, a drugi zmniejszy o 1
Wpisz w wyznaczone miejsce odpowiednie wyrażenie.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 38
R18FpvdSnoTsJ
Ile najmniej centymetrów listewki o szerokości 1 cm należy kupić, aby wykonać ramkę na zdjęcie o wymiarach 203 mm × 254 mm?
Wpisz w lukę odpowiednią liczbę. Do wykonania ramki na zdjęcia potrzebne jest Tu uzupełnij cm listewki.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1JOU7rwId7dC
Ćwiczenie 39
Uzupełnij zdania, przeciągając w luki odpowiednie liczby lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. Suma miar kątów wewnętrznych w czworokącie jest równa 1. 360°, 2. 180°, 3. ma wszystkie boki równej długości, 4. dowolnym trójkącie, 5. równoległych, 6. wszystkich boków wielokąta, 7. prostopadłe, 8. równe.
Suma miar kątów przyległych jest równa 1. 360°, 2. 180°, 3. ma wszystkie boki równej długości, 4. dowolnym trójkącie, 5. równoległych, 6. wszystkich boków wielokąta, 7. prostopadłe, 8. równe.
Romb 1. 360°, 2. 180°, 3. ma wszystkie boki równej długości, 4. dowolnym trójkącie, 5. równoległych, 6. wszystkich boków wielokąta, 7. prostopadłe, 8. równe.
Tory kolejowe to przykład dwóch prostych 1. 360°, 2. 180°, 3. ma wszystkie boki równej długości, 4. dowolnym trójkącie, 5. równoległych, 6. wszystkich boków wielokąta, 7. prostopadłe, 8. równe.
Mówimy, że dwie proste są 1. 360°, 2. 180°, 3. ma wszystkie boki równej długości, 4. dowolnym trójkącie, 5. równoległych, 6. wszystkich boków wielokąta, 7. prostopadłe, 8. równe, gdy dwa krótsze boki ekierki przylegają do badanych linii.
Obwód to suma długości1. 360°, 2. 180°, 3. ma wszystkie boki równej długości, 4. dowolnym trójkącie, 5. równoległych, 6. wszystkich boków wielokąta, 7. prostopadłe, 8. równe.
Kąty wierzchołkowe są 1. 360°, 2. 180°, 3. ma wszystkie boki równej długości, 4. dowolnym trójkącie, 5. równoległych, 6. wszystkich boków wielokąta, 7. prostopadłe, 8. równe.
Suma kątów wewnętrznych wynosi 180° w 1. 360°, 2. 180°, 3. ma wszystkie boki równej długości, 4. dowolnym trójkącie, 5. równoległych, 6. wszystkich boków wielokąta, 7. prostopadłe, 8. równe.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RSiPxKEPjvcCp
Ćwiczenie 40
Uzupełnij zdania, przeciągając w luki odpowiednie liczby lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. Suma miar kątów wewnętrznych w czworokącie jest równa 1. 360°, 2. 180°, 3. ma wszystkie boki równej długości, 4. dowolnym trójkącie, 5. równoległych, 6. wszystkich boków wielokąta, 7. prostopadłe, 8. równe.
Suma miar kątów przyległych jest równa 1. 360°, 2. 180°, 3. ma wszystkie boki równej długości, 4. dowolnym trójkącie, 5. równoległych, 6. wszystkich boków wielokąta, 7. prostopadłe, 8. równe.
Romb 1. 360°, 2. 180°, 3. ma wszystkie boki równej długości, 4. dowolnym trójkącie, 5. równoległych, 6. wszystkich boków wielokąta, 7. prostopadłe, 8. równe.
Tory kolejowe to przykład dwóch prostych 1. 360°, 2. 180°, 3. ma wszystkie boki równej długości, 4. dowolnym trójkącie, 5. równoległych, 6. wszystkich boków wielokąta, 7. prostopadłe, 8. równe.
Mówimy, że dwie proste są 1. 360°, 2. 180°, 3. ma wszystkie boki równej długości, 4. dowolnym trójkącie, 5. równoległych, 6. wszystkich boków wielokąta, 7. prostopadłe, 8. równe, gdy dwa krótsze boki ekierki przylegają do badanych linii.
Obwód to suma długości1. 360°, 2. 180°, 3. ma wszystkie boki równej długości, 4. dowolnym trójkącie, 5. równoległych, 6. wszystkich boków wielokąta, 7. prostopadłe, 8. równe.
Kąty wierzchołkowe są 1. 360°, 2. 180°, 3. ma wszystkie boki równej długości, 4. dowolnym trójkącie, 5. równoległych, 6. wszystkich boków wielokąta, 7. prostopadłe, 8. równe.
Suma kątów wewnętrznych wynosi 180° w 1. 360°, 2. 180°, 3. ma wszystkie boki równej długości, 4. dowolnym trójkącie, 5. równoległych, 6. wszystkich boków wielokąta, 7. prostopadłe, 8. równe.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R13YDHtcIyc1n
Ćwiczenie 41
Rozstrzygnij, czy zdanie jest prawdziwe, czy fałszywe. Możliwe odpowiedzi: 1. Kąt rozwarty ma więcej niż 180° i mniej niż 360°., 2. Jeżeli jeden z kątów przyległych ma 37°, to drugi kąt ma miarę 143°.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RxPbyoWhRdKL4
Ćwiczenie 42
Uzupełnij poniższe zdania podanymi wartościami. Kliknij w lukę, aby rozwinąć listę i wybierz poprawną odpowiedź w każdym przypadku. Średnica okręgu o promieniu 6 cm ma długość 1. 12 cm, 2. 9 cm, 3. 4 cm, 4. 3 cm.Cięciwa okręgu o promieniu 4 cm nie może mieć długości 1. 12 cm, 2. 9 cm, 3. 4 cm, 4. 3 cm.

Wybierz.

4 cm, 12 cm, 9 cm, 3 cm

a) Średnica okręgu o promieniu 6cm ma długość ............
b) Cięciwa okręgu o promieniu 4cm nie może mieć długości ............

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RAQjp1vut9P4f
Ćwiczenie 43
Uzupełnij poniższe zdania podanymi wartościami. Kliknij w lukę, aby rozwinąć listę i wybierz poprawną odpowiedź w każdym przypadku. Dwa kąty trójkąta mają miary 35° i 75°. Trzeci kąt tego trójkąta ma miarę 1. 69°, 2. 85°, 3. 70°, 4. 71°.Kąt między ramionami trójkąta równoramiennego ma miarę 42°. Kąt przy podstawie tego trójkąta ma miarę 1. 69°, 2. 85°, 3. 70°, 4. 71°.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1YSi7WbUVuUD
Ćwiczenie 44
Uzupełnij luki w zdaniach, wpisując odpowiednie liczby. Jeśli w trójkącie prostokątnym jeden z kątów ma miarę 60°, to najmniejszy z kątów ma miarę Tu uzupełnij°W trójkącie prostokątnym równoramiennym miary kątów wynoszą: 90°, Tu uzupełnij° oraz Tu uzupełnij°.Jeśli w trójkącie równoramiennym rozwartokątnym jeden z kątów ma miarę 110°, to pozostałe dwa kąty mają miary Tu uzupełnij° oraz Tu uzupełnij°.Jeśli w trójkącie równoramiennym dwa z kątów mają miary 50° oraz 80°, to trzeci kąt ma miarę Tu uzupełnij°.

Uzupełnij.

a) Jeśli w trójkącie prostokątnym jeden z kątów ma miarę 60°, to najmniejszy z kątów ma miarę ............ °
b) W trójkącie prostokątnym równoramiennym miary kątów wynoszą: 90°, ............ ° oraz ............ °.
c) Jeśli w trójkącie równoramiennym rozwartokątnym jeden z kątów ma miarę 110°, to pozostałe dwa kąty mają miary ............ ° oraz ............°.
d) Jeśli w trójkącie .............................. dwa z kątów mają miary 50° oraz 80°, to trzeci kąt ma miarę ............ °.

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R50DqscTQebL6
Ćwiczenie 45
Czy z odcinków o długości 1 m, 2 m, 3 m można skonstruować trójkąt?
Wybierz z listy poprawną odpowiedź na powyższe pytanie oraz poprawne uzasadnienie. Kliknij w lukę, aby rozwinąć listę i wybierz poprawną odpowiedź. Odpowiedź: 1. suma długości dwóch krótszych odcinków jest większa od długości najdłuższego odcinka., 2. suma długości dwóch krótszych odcinków jest równa długości najdłuższego odcinka., 3. Nie, 4. Tak , ponieważ 1. suma długości dwóch krótszych odcinków jest większa od długości najdłuższego odcinka., 2. suma długości dwóch krótszych odcinków jest równa długości najdłuższego odcinka., 3. Nie, 4. Tak

Wybierz z listy poprawną odpowiedź na poniższe pytanie oraz poprawne uzasadnienie.

Tak, suma długości dwóch krótszych odcinków jest równa długości najdłuższego odcinka., Nie, suma długości dwóch krótszych odcinków jest większa od długości najdłuższego odcinka.

Czy z odcinków o długości 1m, 2m, 3m można skonstruować trójkąt ?

.............................................................................................................................................................................................. , ponieważ ..............................................................................................................................................................................................

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1euMHG91LTZI
Ćwiczenie 46
Rozstrzygnij, czy zdanie jest prawdziwe, czy fałszywe. Możliwe odpowiedzi: 1. W każdym rombie przekątne są prostopadłe., 2. Prostokąt to czworokąt, który ma wszystkie kąty proste., 3. Czworokąt, który ma tylko jedną parę boków równoległych to równoległobok., 4. Każdy kwadrat jest trapezem.

  • W każdym rombie przekątne są prostopadłe.
  • Prostokąt to czworokąt, który ma wszystkie kąty proste.
  • Czworokąt, który ma tylko jedną parę boków równoległych to równoległobok.
  • Każdy kwadrat jest trapezem.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 47

Wielokąty przedstawione na rysunku to: romb, trapez i równoległobok.

RIY8dycikNCIx1
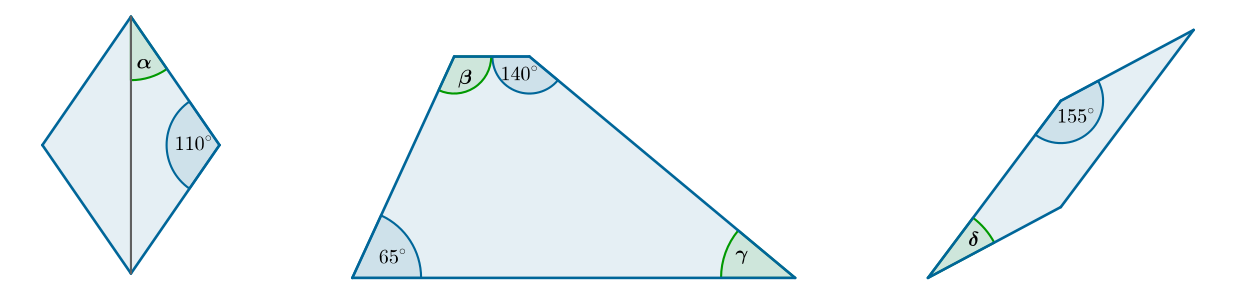
Rysunek trzech czworokątów. Pierwsza figura to romb podzielony dłuższą przekątną na dwa jednakowe trójkąty. Zaznaczony kąt 110 stopni między bokami rombu i kąt alfa między przekątną a bokiem rombu. Druga figura to trapez, w którym kąty przy jednym ramieniu są równe 65 stopni i beta oraz przy drugim ramieniu 140 stopni i gamma. Trzecia figura to równoległobok o kątach 155 stopni i delta.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1V3du5UPvGOL
Jakie miary mają kąty α, β, γ i δ?
Wskaż poprawną odpowiedź. Możliwe odpowiedzi: 1. α=35°, β=40°, γ=65°, δ=35°, 2. α=55°, β=115°, γ=40°, δ=35°, 3. α=35°, β=115°, γ=40°, δ=25°, 4. α=55°, β=40°, γ=115°, δ=25°
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
ROrJc6LnZCciL
Ćwiczenie 48
Obwód trójkąta równoramiennego wynosi 38 . Oblicz długość ramienia tego trójkąta, jeżeli stanowi ono 34 długości podstawy.
Zaznacz prawidłową odpowiedź. Możliwe odpowiedzi: 1. 11,4, 2. 10,7, 3. 8,5, 4. 13,9
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 49

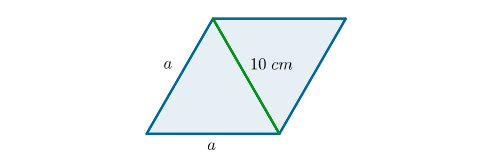
Przekątna rombu o długości 10 cm dzieli go na dwa trójkąty o obwodach 30 cm.

ROTLlkcgW67HX1
Rysunek rombu o boku a i przekątnej 10 cm.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1IDYfhb7eKYH
Jaki jest obwód tego rombu? Wskaż poprawną odpowiedź. Możliwe odpowiedzi: 1. 20 cm, 2. 40 cm, 3. 50 cm, 4. 60 cm

  • 20 cm
  • 40 cm
  • 50 cm
  • 60 cm
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1TpTjQNoColn
Ćwiczenie 50
W kwadracie o boku 6 cm dwa równoległe boki zwiększono o 13 dotychczasowej długości, a pozostałe dwa zmniejszono o połowę i otrzymano prostokąt.
Uzupełnij luki w zdaniach podanymi liczbami. Kliknij w lukę, aby rozwinąć listę i wybierz poprawną odpowiedź w każdym przypadku. Pole tego prostokąta jest mniejsze od pola kwadratu o 1. 23, 2. 32, 3. 15, 4. 9, 5. 53, 6. 12cm2.Pole otrzymanego prostokąta stanowi 1. 23, 2. 32, 3. 15, 4. 9, 5. 53, 6. 12 pola kwadratu.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1LM3gpu5FEQa
Ćwiczenie 51
Trapez równoramienny i prostokąt, przedstawione na poniższym rysunku, mają równe obwody. Oblicz długość ramienia tego trapezu i zaznacz prawidłową odpowiedź, jeśli promienie kół rozmieszczonych w prostokącie mają po 5 cm długości. Możliwe odpowiedzi: 1. 40 cm, 2. 35 cm, 3. 45 cm, 4. 65 cm
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 52

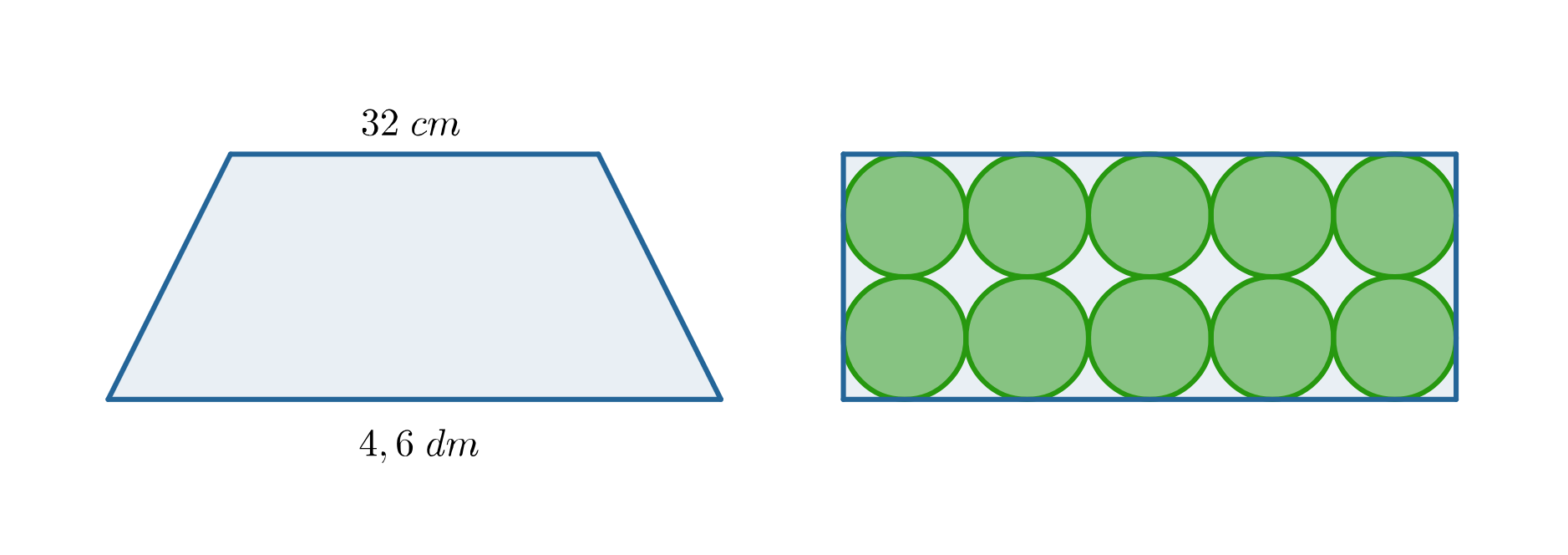
Trapez równoramienny i prostokąt, przedstawione na poniższym rysunku, mają równe obwody. Oblicz długość ramienia tego trapezu, jeśli promienie kół rozmieszczonych w prostokącie mają po 5 cm długości.

RDUbcCvnTPtOr1
Rysunek trapezu równoramiennego i prostokąta. Trapez ma podstawy długości 32 cm i 4,6 dm oraz wysokość równą krótszemu bokowi prostokąta. W prostokącie umieszczone jest 10 kół po pięć w dwóch rzędach. Dłuższy bok prostokąta równy jest długości dziesięciu promieni kół, a krótszy bok prostokąta jest równy długości czterech promieni kół.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R15lq3AOpE39V
Zaznacz poprawną odpowiedź. Możliwe odpowiedzi: 1. 31 cm, 2. 35 cm, 3. 25 cm, 4. 33 cm
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1Hd0wl6B8G9v
Ćwiczenie 53
Kąt przyległy do kąta α jest od niego o 35° mniejszy. Oblicz miarę kąta α i zaznacz prawidłową odpowiedź. Możliwe odpowiedzi: 1. 107,5°, 2. 109,5°, 3. 99°, 4. 112°
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 54

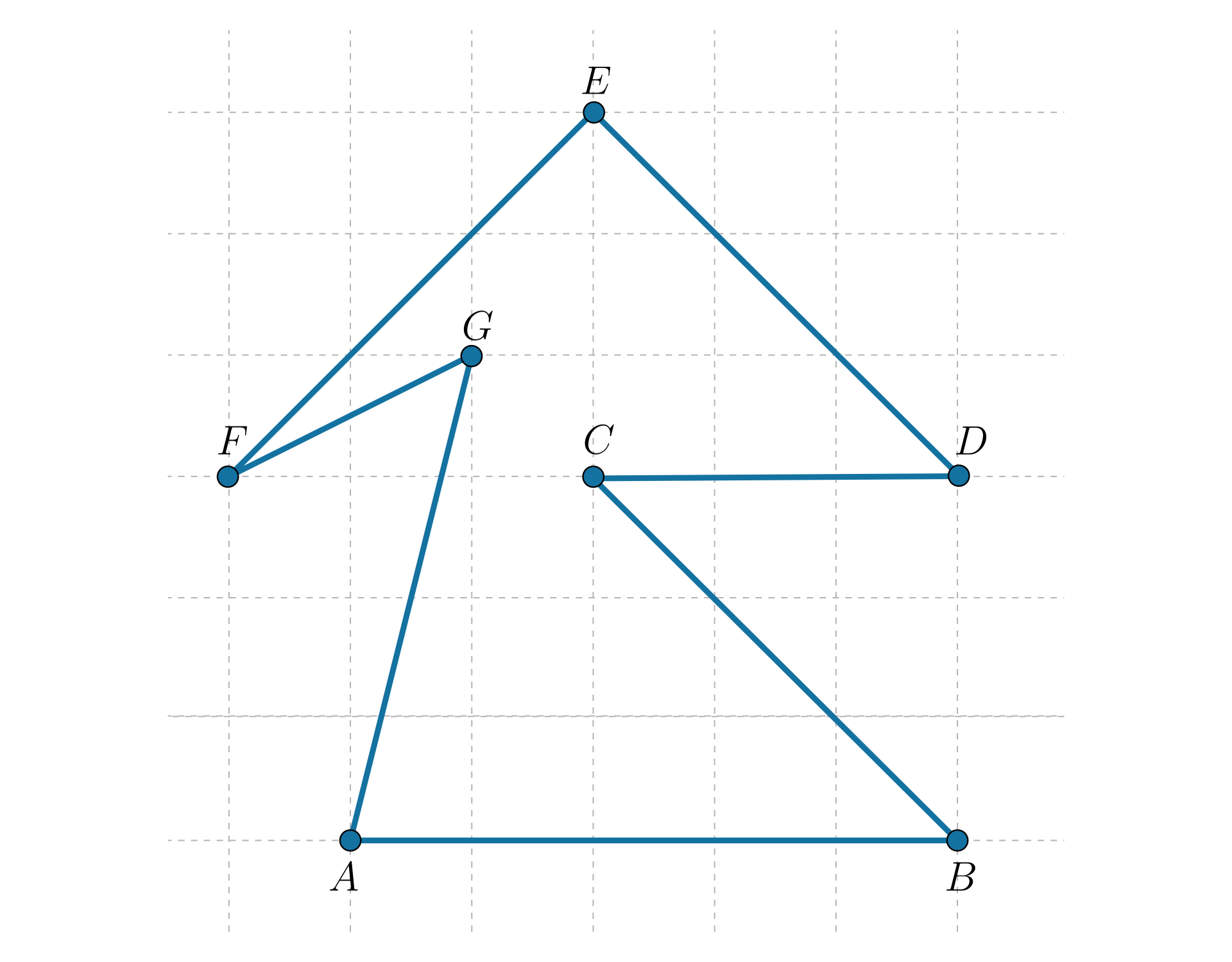
Na poniższym rysunku przedstawiono siedmiokąt ABCDEFG.

RLZokSwqQKXt9
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1ACiKo5s6KjF
Łączenie par. Oceń prawdziwość poniższych zdań. Przy każdym zdaniu w tabeli zaznacz Prawda albo Fałsz.. W powyższym siedmiokącie są trzy pary boków równoległych.. Możliwe odpowiedzi: Prawda, Fałsz. W powyższym siedmiokącie są dwie pary boków prostopadłych.. Możliwe odpowiedzi: Prawda, Fałsz. Powyższy siedmiokąt ma cztery kąty ostre, jeden kąt prosty i dwa kąty rozwarte.. Możliwe odpowiedzi: Prawda, Fałsz
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1dW15HMU0rFN
Wielokąt foremny to taki, którego boki są równe. Wiedząc to, zaznacz wszystkie zdania prawdziwe. Możliwe odpowiedzi: 1. Kwadrat to czworokąt foremny., 2. W sześciokącie foremnym znajdziemy boki, które są równoległe., 3. W pięciokącie foremnym znajdziemy boki, które są równoległe., 4. Trójkąt równoboczny jest wielokątem foremnym.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 55

Zapoznaj się z poniższym rysunkiem. Jakie kąty przedstawia?

R1KslGbw9B3PR
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R78Bl7HkSDEfq
Uzupełnij poniższe luki. Kliknij w nie, aby rozwinąć listę, a następnie wybierz poprawną odpowiedź. Kąt α oraz kąt, który ma miarę 35°, to kąty 1. 145°, 2. wierzchołkowe, 3. 110°, 4. 35°, 5. przyległe, 6. 75°, 7. 360°, 8. naprzemianległe, 9. odpowiadające, 10. 285°, 11. 180°, 12. 70° zatem kąt α ma miarę 1. 145°, 2. wierzchołkowe, 3. 110°, 4. 35°, 5. przyległe, 6. 75°, 7. 360°, 8. naprzemianległe, 9. odpowiadające, 10. 285°, 11. 180°, 12. 70°.Kąt β oraz kąt, który ma miarę 110°, to kąty 1. 145°, 2. wierzchołkowe, 3. 110°, 4. 35°, 5. przyległe, 6. 75°, 7. 360°, 8. naprzemianległe, 9. odpowiadające, 10. 285°, 11. 180°, 12. 70° zatem kąt β ma miarę 1. 145°, 2. wierzchołkowe, 3. 110°, 4. 35°, 5. przyległe, 6. 75°, 7. 360°, 8. naprzemianległe, 9. odpowiadające, 10. 285°, 11. 180°, 12. 70°.Suma kątów w trójkącie wynosi 1. 145°, 2. wierzchołkowe, 3. 110°, 4. 35°, 5. przyległe, 6. 75°, 7. 360°, 8. naprzemianległe, 9. odpowiadające, 10. 285°, 11. 180°, 12. 70°, więc kąt γ ma miarę 1. 145°, 2. wierzchołkowe, 3. 110°, 4. 35°, 5. przyległe, 6. 75°, 7. 360°, 8. naprzemianległe, 9. odpowiadające, 10. 285°, 11. 180°, 12. 70°.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RWMCQdoTTa1CQ
Mając podane miary pewnych kątów, oceń jakie to kąty, łącząc je w pary z odpowiednimi pojęciami. kąty o miarach: 16° i 16° Możliwe odpowiedzi: 1. kąty wierzchołkowe, 2. kąty dopełniające się, 3. kąty przyległe kąty o miarach: 30° i 150° Możliwe odpowiedzi: 1. kąty wierzchołkowe, 2. kąty dopełniające się, 3. kąty przyległe kąty o miarach: 70° i 20° Możliwe odpowiedzi: 1. kąty wierzchołkowe, 2. kąty dopełniające się, 3. kąty przyległe
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 56

Jakimi trójkątami są te przedstawione na poniższym rysunku?

RU1KFoOktyq4n
Ilustracja przedstawia cztery trójkąty narysowane na tle w kratkę. Trójkąt pierwszy ma następujące boki: bok pionowy, który jest wysokością, o długości dwóch kratek, poziomą podstawę o długości dwóch kratek i bok ukośny o długość pierwiastek z dwóch kratek. Trójkąt drugi ma poziomą postawę o długości dwóch kratek, pionową wysokość na trzy kratki dzielącą podstawę na pół. Trzeci trójkąt ma poziomą podstawę o długości czterech kratek, pionową wysokość o długości jeden dzielącą podstawę na pół. Czwarty trójkąt ma poziomą podstawę o długości czterech kratek i pionową wysokość o długości dwóch kratek dzielącą podstawę na pół.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1s1BkmAjMncr
Zaznacz poprawną odpowiedź. Możliwe odpowiedzi: 1. Są trójkątami ostrokątnymi., 2. Są trójkątami różnobocznymi., 3. Są trójkątami rozwartokątnymi., 4. Są trójkątami równoramiennymi.

  • ostrokątnymi
  • różnobocznymi
  • rozwartokątnymi
  • równoramiennymi
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 57

Zapoznaj się z poniższym rysunkiem i znajdź wśród nich dwa o tej samej cesze.

R1dl7kGAazkOH
Ilustracja przedstawia cztery trójkąty narysowane na tle w kratkę. Trójkąt pierwszy ma następujące boki: bok pionowy, który jest wysokością, o długości dwóch kratek, poziomą podstawę o długości dwóch kratek i bok ukośny o długość pierwiastek z dwóch kratek. Trójkąt drugi ma poziomą postawę o długości dwóch kratek, pionową wysokość na trzy kratki dzielącą podstawę na pół. Trzeci trójkąt ma poziomą podstawę o długości czterech kratek, pionową wysokość o długości jeden dzielącą podstawę na pół. Czwarty trójkąt ma poziomą podstawę o długości czterech kratek i pionową wysokość o długości dwóch kratek dzielącą podstawę na pół.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R5XcpgNgXAlbi
Zaznacz poprawną odpowiedź. Możliwe odpowiedzi: 1. Na rysunku przedstawiono dwa trójkąty różnoboczne., 2. Na rysunku przedstawiono dwa trójkąty prostokątne., 3. Na rysunku przedstawiono dwa trójkąty rozwartokątne., 4. Na rysunku przedstawiono dwa trójkąty równoboczne.

  • różnoboczne
  • prostokątne
  • rozwartokątne
  • równoboczne
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R10UtRUEWFxAz
Ćwiczenie 58
Odcinki o długościach 5 cm i 3 cm są bokami trójkąta. Jaką długość może mieć trzeci bok tego trójkąta? Wskaż wszystkie poprawne odpowiedzi. Możliwe odpowiedzi: 1. 1 cm, 2. 3 cm, 3. 6 cm, 4. 9 cm

  • 1  cm
  • 3  cm
  • 6  cm
  • 9  cm
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1VdSs9HLwoup
Ćwiczenie 59
W których czworokątach przekątne są równej długości? Możliwe odpowiedzi: 1. W kwadracie., 2. W prostokącie., 3. W rombie., 4. W równoległoboku.

  • w kwadracie
  • w prostokącie
  • w rombie
  • w równoległoboku
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RZRkuSb628wLD
Ćwiczenie 60
W których czworokątach obie przekątne przecinają się w połowie? Możliwe odpowiedzi: 1. W kwadracie., 2. W prostokącie., 3. W rombie., 4. W równoległoboku.

  • w kwadracie
  • w prostokącie
  • w rombie
  • w równoległoboku
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RBiEhGJFL63Un
Ćwiczenie 61
W których czworokątach przekątne są prostopadłe? Możliwe odpowiedzi: 1. W kwadracie., 2. W prostokącie., 3. W rombie., 4. W równoległoboku.

  • w kwadracie
  • w prostokącie
  • w rombie
  • w równoległoboku
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 62

Trapez AEFD zbudowany jest z trapezu ABCD i równoległoboku BEFC.

RidKlSA5zkyy61
Ilustracja przedstawia trapez A B C D i równoległobok B C E F, który ma z nim jeden wspólny bok będący prawym ramieniem trapezu i jednocześnie lewym ukośnym bokiem równoległoboku. Jest to odcinek B C. Przy niektórych wierzchołkach obu figur oznaczono kąty wewnętrzne. W trapezie: przy lewym dolnym wierzchołku A oznaczono kąt 50 stopni między lewym ramieniem a dolną podstawą i przy wierzchołku D oznaczono kąt rozwarty alfa między lewym ramieniem a górną podstawą trapezu. W równoległoboku oznaczono natomiast trzy kąty. Kąt przy wierzchołku B między prawym a dolnym bokiem figury to kąt 100 stopni, kąt przy wierzchołku E między dolnym a lewym bokiem to kąt ostry gamma oraz kąt rozwarty beta przy wierzchołku F między prawym a górnym bokiem równoległoboku.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R12jCvf4xCjAa
Wykorzystaj dane z powyższego rysunku i oblicz miary kątów α, β i γ czworokąta AEFD.
Uzupełnij poniższe luki. Kliknij w nie, aby rozwinąć listę, a następnie wybierz poprawną odpowiedź. α=1. 80°, 2. 100°, 3. 70°, 4. 130°, 5. 120°, 6. 135°, 7. 90°β= 1. 80°, 2. 100°, 3. 70°, 4. 130°, 5. 120°, 6. 135°, 7. 90°γ=1. 80°, 2. 100°, 3. 70°, 4. 130°, 5. 120°, 6. 135°, 7. 90°
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 63

Rysunek przedstawia okrąg o środku A.

R1PGEX3mWkiV01
Grafika statyczna
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R10CZG9aoGSzs
cięciwa okręgu Możliwe odpowiedzi: 1. CE, 2. CD, CE, 3. AC, AE, AB promienie okręgu Możliwe odpowiedzi: 1. CE, 2. CD, CE, 3. AC, AE, AB średnica okręgu Możliwe odpowiedzi: 1. CE, 2. CD, CE, 3. AC, AE, AB
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RINswYll00A4y
Uzupełnij poniższe luki. Kliknij w nie, aby rozwinąć listę, a następnie wybierz poprawną odpowiedź. Jest ściśle określonym punktem koła. To 1. prosta, 2. okręgiem, 3. cięciwa, 4. na zewnątrz, 5. środek, 6. dwusieczna, 7. średnica, 8. okręgu, 9. kawałek, 10. obszar, 11. promień, 12. półprosta, 13. wewnątrz koła.To odcinek należący do koła. Ma ściśle określoną długość. Jest to 1. prosta, 2. okręgiem, 3. cięciwa, 4. na zewnątrz, 5. środek, 6. dwusieczna, 7. średnica, 8. okręgu, 9. kawałek, 10. obszar, 11. promień, 12. półprosta, 13. wewnątrz.To odcinek należący do koła. Może być krótszy lub dłuższy od promienia koła. Jest to 1. prosta, 2. okręgiem, 3. cięciwa, 4. na zewnątrz, 5. środek, 6. dwusieczna, 7. średnica, 8. okręgu, 9. kawałek, 10. obszar, 11. promień, 12. półprosta, 13. wewnątrz.Najdłuższą cięciwą koła jest 1. prosta, 2. okręgiem, 3. cięciwa, 4. na zewnątrz, 5. środek, 6. dwusieczna, 7. średnica, 8. okręgu, 9. kawałek, 10. obszar, 11. promień, 12. półprosta, 13. wewnątrz przechodząca przez jego środek.Koło to 1. prosta, 2. okręgiem, 3. cięciwa, 4. na zewnątrz, 5. środek, 6. dwusieczna, 7. średnica, 8. okręgu, 9. kawałek, 10. obszar, 11. promień, 12. półprosta, 13. wewnątrz znajdujący się 1. prosta, 2. okręgiem, 3. cięciwa, 4. na zewnątrz, 5. środek, 6. dwusieczna, 7. średnica, 8. okręgu, 9. kawałek, 10. obszar, 11. promień, 12. półprosta, 13. wewnątrz pewnego 1. prosta, 2. okręgiem, 3. cięciwa, 4. na zewnątrz, 5. środek, 6. dwusieczna, 7. średnica, 8. okręgu, 9. kawałek, 10. obszar, 11. promień, 12. półprosta, 13. wewnątrz wraz z tym 1. prosta, 2. okręgiem, 3. cięciwa, 4. na zewnątrz, 5. środek, 6. dwusieczna, 7. średnica, 8. okręgu, 9. kawałek, 10. obszar, 11. promień, 12. półprosta, 13. wewnątrz.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Notatnik

Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.

R1b8OvSPUG8s3
(Uzupełnij).
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
9. Koła i okręgi
Pola wielokątów