R1KArxESX7CXy
Rysunek przedstawia boisko. Na końcu boiska jest kosz do koszykówki. Napis: Wielokąty, koła i okręgi.

Wielokąty, koła i okręgi

Źródło: Santiago Pagnotta, dostępny w internecie: https://pexels.com/, domena publiczna.

8. Klasyfikacja czworokątów

Klasyfikacja to podział, na przykład figur, na grupy według określonej zasady. W tym materiale sprawdzisz, jak sobie radzisz z klasyfikowaniem czworokątów.

Nim przystąpisz do wykonywania ćwiczeń zapoznaj się z poniższym filmem, który pokazuje w jaki sposób grupujemy czworokąty ze względu na ich własności.

RzdiR0YYO1kVO1
Animacja przedstawia w jaki sposób klasyfikujemy różne czworokąty.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Film dostępny pod adresem /preview/resource/RzdiR0YYO1kVO

Klasyfikacja czworokatow_4001
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

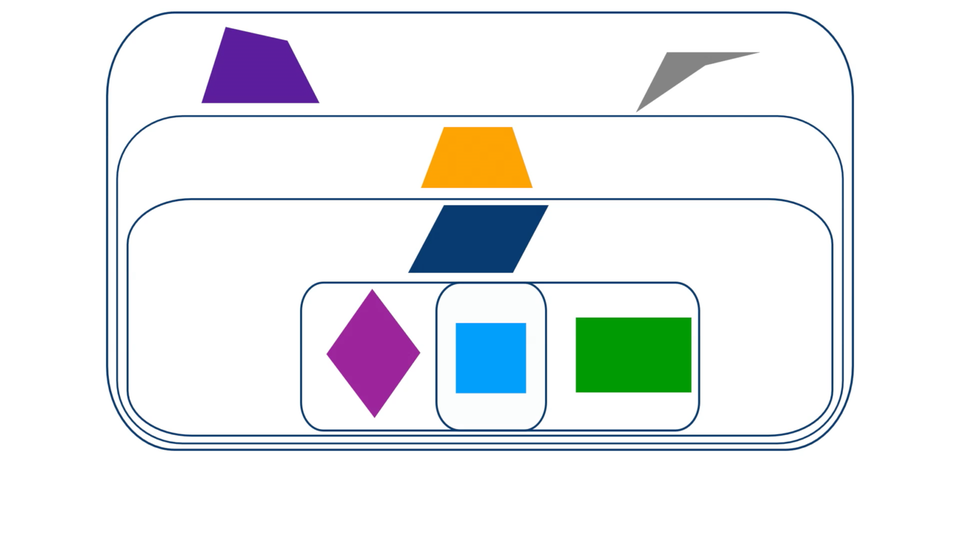
Animacja przedstawia w jaki sposób klasyfikujemy różne czworokąty.

1
Ćwiczenie 1
R1Al5HTI5ODFh
Uzupełnij poniższą tabelę wpisując w odpowiednie komórki T (tak) lub N (nie), określając w ten sposób, czy nazwa figury z boku tabeli odpowiada danemu rysunkowi.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RWWP5jQ1WOe1k
Odpowiedz na pytania wpisując "Tak" albo "Nie" w puste pole. Czy każdy kwadrat jest prostokątem? Tu uzupełnijCzy każdy kwadrat jest rombem? Tu uzupełnijCzy każdy kwadrat jest równoległobokiem? Tu uzupełnijCzy każdy kwadrat jest trapezem? Tu uzupełnijCzy każdy prostokąt jest kwadratem? Tu uzupełnijCzy każdy prostokąt jest rombem? Tu uzupełnijCzy każdy prostokąt jest równoległobokiem? Tu uzupełnijCzy każdy prostokąt jest trapezem? Tu uzupełnijCzy każdy romb jest kwadratem? Tu uzupełnijCzy każdy romb jest prostokątem? Tu uzupełnijCzy każdy romb jest równoległobokiem? Tu uzupełnijCzy każdy romb jest trapezem? Tu uzupełnijCzy każdy równoległobok jest kwadratem? Tu uzupełnijCzy każdy równoległobok jest prostokątem? Tu uzupełnijCzy każdy równoległobok jest rombem? Tu uzupełnijCzy każdy równoległobok jest trapezem? Tu uzupełnijCzy każdy trapez jest kwadratem? Tu uzupełnijCzy każdy trapez jest prostokątem? Tu uzupełnijCzy każdy trapez jest rombem? Tu uzupełnijCzy każdy trapez jest trapezem? Tu uzupełnij
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RQeElnwyRrOU2
Ćwiczenie 2
Które z czworokątów mają podane własności? Kliknij w lukę aby rozwinąć listę i wybierz prawidłowe odpowiedzi w kolejności alfabetycznej.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1Ruoq4qmO3Eq
(Uzupełnij).
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
1
Ćwiczenie 3
R1bsz25Y7NXKh
Przeciągnij i upuść wybrane nazwy i definicje czworokątów na poniższą grafikę.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1QgU2d8EWHEW
Uzupełnij zdania, przeciągając w luki odpowiednie własności lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. Prostokątem nazywamy czworokąt, który 1. ma dwie pary boków równoległych, 2. jest prostokątem i ma wszystkie boki równej długości, 3. ma przynajmniej jedną parę boków równoległych, 4. jest równoległobokiem i ma wszystkie boki równej długości, 5. ma wszystkie kąty proste.Kwadratem nazywamy czworokąt, który 1. ma dwie pary boków równoległych, 2. jest prostokątem i ma wszystkie boki równej długości, 3. ma przynajmniej jedną parę boków równoległych, 4. jest równoległobokiem i ma wszystkie boki równej długości, 5. ma wszystkie kąty proste.Równoległobokiem nazywamy czworokąt, który 1. ma dwie pary boków równoległych, 2. jest prostokątem i ma wszystkie boki równej długości, 3. ma przynajmniej jedną parę boków równoległych, 4. jest równoległobokiem i ma wszystkie boki równej długości, 5. ma wszystkie kąty proste.Rombem nazywamy czworokąt, który 1. ma dwie pary boków równoległych, 2. jest prostokątem i ma wszystkie boki równej długości, 3. ma przynajmniej jedną parę boków równoległych, 4. jest równoległobokiem i ma wszystkie boki równej długości, 5. ma wszystkie kąty proste.Trapezem nazywamy czworokąt, który 1. ma dwie pary boków równoległych, 2. jest prostokątem i ma wszystkie boki równej długości, 3. ma przynajmniej jedną parę boków równoległych, 4. jest równoległobokiem i ma wszystkie boki równej długości, 5. ma wszystkie kąty proste.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 4

Rysunek przedstawia różne czworokąty.

RcYbhisFCd4ZO
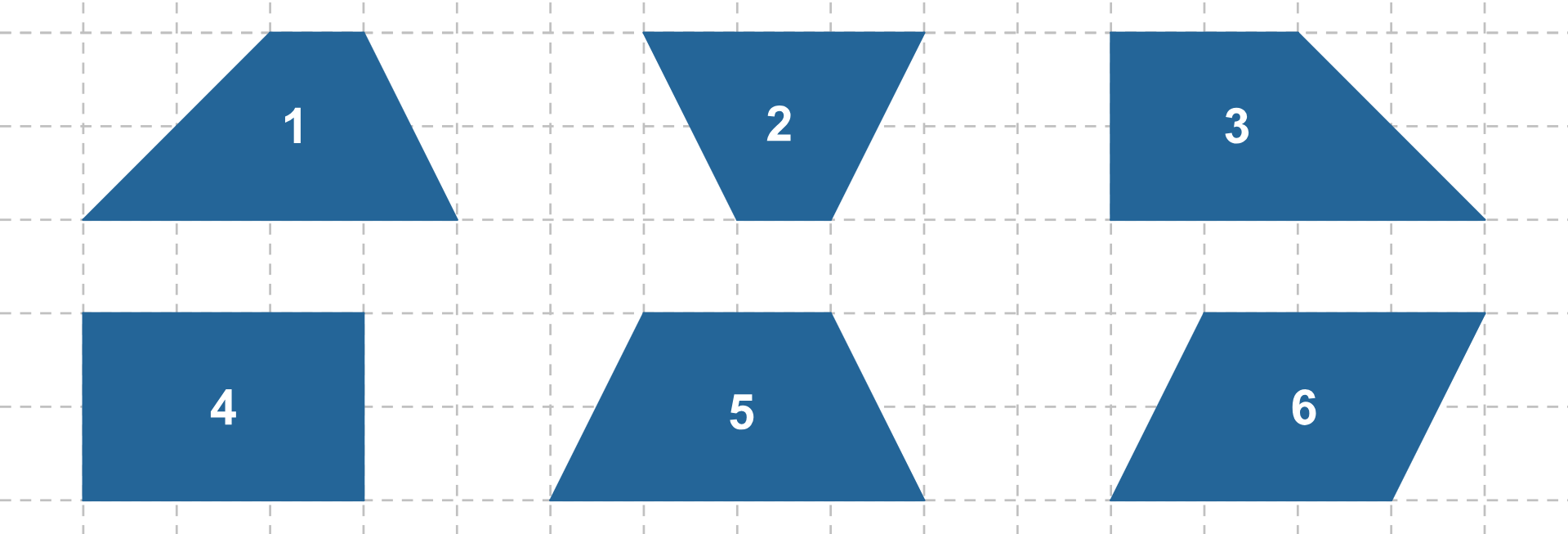
Rysunek sześciu różnych czworokątów. Figura numer 1 ma wszystkie boki różnej długości, z czego jedna para boków jest równoległa. Figura numer 2 ma dwa boki tej samej długości i dwa boki różnej długości, które są równoległe. Figura trzecia ma parę boków, które są równoległe i dwa z czterech kątów wewnętrznych mają miarę 90 stopni. Figura czwarta jest prostokątem. Figura piąta ma kształt trójkąta równoramiennego z odciętą górną częścią. Linia odcięcia jest równoległa do podstawy tej figury. Figura szósta jest równoległobokiem.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Rfs7cBi0JQ7iY
Przyporządkuj figury do odpowiednich grup, a następnie przeciągnij i upuść numer figury do odpowiedniej grupy. Trapezy to figury o numerach: Możliwe odpowiedzi: 1. 6, 2. 4, 3. 4, 4. 1, 5. 3, 6. 2, 7. 2, 8. 3, 9. 6, 10. 5, 11. 4, 12. 5 Trapezy równoramienne to figury o numerach: Możliwe odpowiedzi: 1. 6, 2. 4, 3. 4, 4. 1, 5. 3, 6. 2, 7. 2, 8. 3, 9. 6, 10. 5, 11. 4, 12. 5 Trapezy prostokątne to figury o numerach: Możliwe odpowiedzi: 1. 6, 2. 4, 3. 4, 4. 1, 5. 3, 6. 2, 7. 2, 8. 3, 9. 6, 10. 5, 11. 4, 12. 5
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RN7pw77ieFjEz
Ćwiczenie 5
Uzupełnij zdania, przeciągając w luki odpowiednie słowa lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. Romb, który ma wszystkie kąty proste, to 1. prostokąt, 2. kwadrat, 3. prostokąt, 4. równoległobok, 5. równoległobok, 6. kwadrat, 7. prostokąt, 8. równoległobok, 9. kwadrat.Równoległobok, który ma wszystkie kąty proste, to 1. prostokąt, 2. kwadrat, 3. prostokąt, 4. równoległobok, 5. równoległobok, 6. kwadrat, 7. prostokąt, 8. równoległobok, 9. kwadrat.Trapez, którego podstawy są równej długości, to 1. prostokąt, 2. kwadrat, 3. prostokąt, 4. równoległobok, 5. równoległobok, 6. kwadrat, 7. prostokąt, 8. równoległobok, 9. kwadrat.Trapez prostokątny, którego ramiona są równej długości, to 1. prostokąt, 2. kwadrat, 3. prostokąt, 4. równoległobok, 5. równoległobok, 6. kwadrat, 7. prostokąt, 8. równoległobok, 9. kwadrat.Trapez równoramienny, w którym ramiona są równoległe, to 1. prostokąt, 2. kwadrat, 3. prostokąt, 4. równoległobok, 5. równoległobok, 6. kwadrat, 7. prostokąt, 8. równoległobok, 9. kwadrat.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1bfwFaECTuAK
Ćwiczenie 6
Przeciągnij nazwy czworokątów na odpowiednie pola. Dla każdego wielokąta wybierz tę własność, która najlepiej odróżnia go od innych czworokątów. Przeciwległe boki są równoległe i wszystkie boki są równej długości Możliwe odpowiedzi: 1. trapez, 2. równoległobok, 3. prostokąt, 4. kwadrat, 5. romb Przeciwległe boki są równoległe i równej długości Możliwe odpowiedzi: 1. trapez, 2. równoległobok, 3. prostokąt, 4. kwadrat, 5. romb Dokładnie dwa przeciwległe boki są równoległe Możliwe odpowiedzi: 1. trapez, 2. równoległobok, 3. prostokąt, 4. kwadrat, 5. romb

Przeciągnij i upuść nazwę czworokąta do odpowiedniej własności boków, która wyróżnia go spośród innych czworokątów.

prostokąt, kwadrat, równoległobok, trapez, romb

przeciwległe boki są równoległe i wszystkie boki są równej długości  
przeciwległe boki są równoległe i równej długości  
dwa przeciwległe boki są równoległe  
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1bRLk36NCjdt
Ćwiczenie 7
Przeciągnij nazwy czworokątów na odpowiednie pola. Dla każdego wielokąta wybierz tę własność, która najlepiej odróżnia go od innych czworokątów. Wszystkie kąty mają po 90° Możliwe odpowiedzi: 1. prostokąt, 2. równoległobok, 3. romb, 4. kwadrat, 5. trapez Przeciwległe kąty są równe i suma miar dwóch sąsiednich kątów wynosi 180° Możliwe odpowiedzi: 1. prostokąt, 2. równoległobok, 3. romb, 4. kwadrat, 5. trapez Suma miar kątów przy tym samym ramieniu wynosi 180° Możliwe odpowiedzi: 1. prostokąt, 2. równoległobok, 3. romb, 4. kwadrat, 5. trapez

Przeciągnij i upuść nazwę czworokąta do odpowiedniej własności kątów, która wyróżnia go spośród innych czworokątów.

prostokąt, kwadrat, trapez, równoległobok, romb

wszystkie kąty mają po 90°  
przeciwległe kąty są równe i suma miar dwóch sąsiednich kątów wynosi 180°  
suma miar kątów przy tym samym ramieniu wynosi 180°  
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RS17wRj3cJhNW
Ćwiczenie 8
Ile wynosi suma miar kątów wewnętrznych każdego czworokąta? Zaznacz poprawną odpowiedź. Możliwe odpowiedzi: 1. 180 ° , 2. 270 ° , 3. 360 ° , 4. 450 °

  • 180 °
  • 270 °
  • 360 °
  • 450 °
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 9

Zaznacz wszystkie poprawne odpowiedzi w każdym podpunkcie.

RsuccfxFPvVeu
1) Wskaż czworokąty, które mają przekątne równej długości. Możliwe odpowiedzi: 1. prostokąt, 2. kwadrat, 3. równoległobok, 4. romb, 5. trapez
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RxnrHppnFHDSd
2) Wskaż czworokąty, których przekątne dzielą się na połowy. Możliwe odpowiedzi: 1. prostokąt, 2. kwadrat, 3. równoległobok, 4. romb, 5. trapez
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RMg0U6vpmxymV
3) Wskaż czworokąty, których przekątne są do siebie prostopadłe. Możliwe odpowiedzi: 1. prostokąt, 2. kwadrat, 3. równoległobok, 4. romb, 5. trapez
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R148VuT9mqtCM
Ćwiczenie 10
Rozstrzygnij, które zdanie jest prawdziwe i zaznacz wszystkie poprawne odpowiedzi. Możliwe odpowiedzi: 1. W trapezie równoramiennym, który nie jest równoległobokiem, przekątne są równej długości., 2. W trapezie prostokątnym przekątne są prostopadłe., 3. Trapez prostokątny może mieć dwa kąty ostre., 4. Dwa kąty trapezu równoramiennego mogą mieć miary 54 ° i  126 ° .

  • W trapezie równoramiennym, który nie jest równoległobokiem, przekątne są równej długości.
  • W trapezie prostokątnym przekątne są prostopadłe.
  • Trapez prostokątny może mieć dwa kąty ostre.
  • Dwa kąty trapezu równoramiennego mogą mieć miary 54 ° i  126 ° .
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
1
1
Ćwiczenie 11

Uruchom aplet i wykonaj zawarte w nim polecenia. W każdym podpunkcie sprawdź poprawność zadania wciskając przycisk z niebieskim haczykiem.

RFkWZa3GzvKBT1
"1. Animacja pokazuje czworokąt A B C D, w którym poprowadzone są przekątne AC i BD. Zmieniając położenie punktów B i D, należy tak ustawić odcinek BD, aby: był on drugą przekątną równoległoboku A B C D, który nie jest prostokątem
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RfrT382hAY2wu
Ćwiczenie 11
Własności których czworokątów spełnia dowolny prostokąt? Zaznacz wszystkie poprawne odpowiedzi. Możliwe odpowiedzi: 1. Trapezu, 2. Kwadratu, 3. Rombu, 4. Równoległoboku
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 12
RH4bsd5YdChlL
Jeden z kątów równoległoboku ma miarę 35°. Uzupełnij rosnąco miary pozostałych kątów tego równoległoboku wpisując ich wartości w puste pola. Odpowiedź: Miary pozostałych kątów równoległoboka wynoszą Tu uzupełnij°, Tu uzupełnij° i Tu uzupełnij°.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 13
RCASICumE4nfA
Jeden z kątów trapezu równoramiennego ma miarę 50°. Uzupełnij rosnąco miary pozostałych kątów tego trapezu wpisując liczby w puste pola. Odpowiedź: Miary pozostałych kątów trapezu wynoszą Tu uzupełnij°, Tu uzupełnij° i Tu uzupełnij°.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 14
RJj5Ljqt6fqmm
Jeden z kątów trapezu prostokątnego ma miarę 118°. Uzupełnij rosnąco miary pozostałych kątów tego trapezu wpisując liczby w puste pola. Odpowiedź: Miary pozostałych kątów trapezu wynoszą Tu uzupełnij°, Tu uzupełnij°, Tu uzupełnij°
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 15

Wielokąt ABCDEF zbudowany jest z dwóch jednakowych równoległoboków.

RX0yZvseB8XmR1
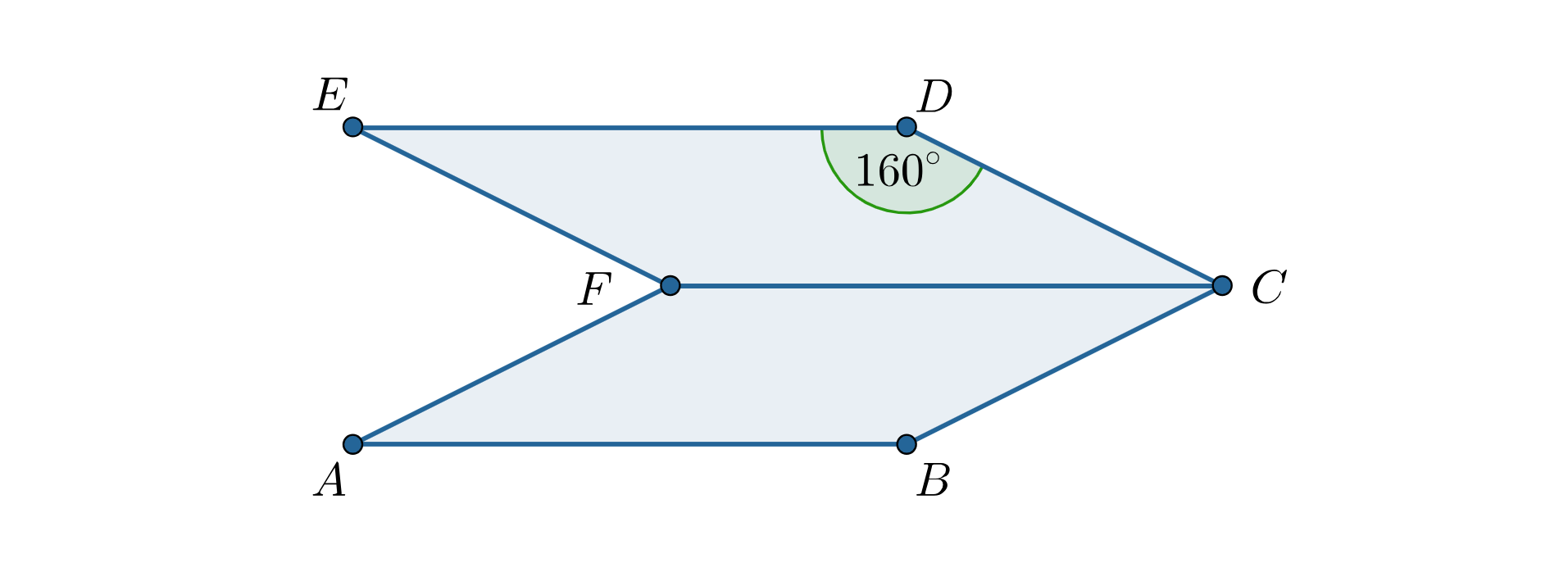
Rysunek wielokąta A B C D E F zbudowanego z dwóch jednakowych równoległoboków F C D E i A B C F o wspólnym boku FC. Zaznaczony kąt wewnętrzny C D E o mierze 160 stopni.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RJxPQKQbsYbOf
Połącz w pary kąt oraz jego miarę. ∡FAB Możliwe odpowiedzi: 1. 20°, 2. 160°, 3. 20°, 4. 320°, 5. 160° ∡ABC Możliwe odpowiedzi: 1. 20°, 2. 160°, 3. 20°, 4. 320°, 5. 160° ∡CDE Możliwe odpowiedzi: 1. 20°, 2. 160°, 3. 20°, 4. 320°, 5. 160° ∡DEF Możliwe odpowiedzi: 1. 20°, 2. 160°, 3. 20°, 4. 320°, 5. 160° ∡EFA Możliwe odpowiedzi: 1. 20°, 2. 160°, 3. 20°, 4. 320°, 5. 160°
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 16

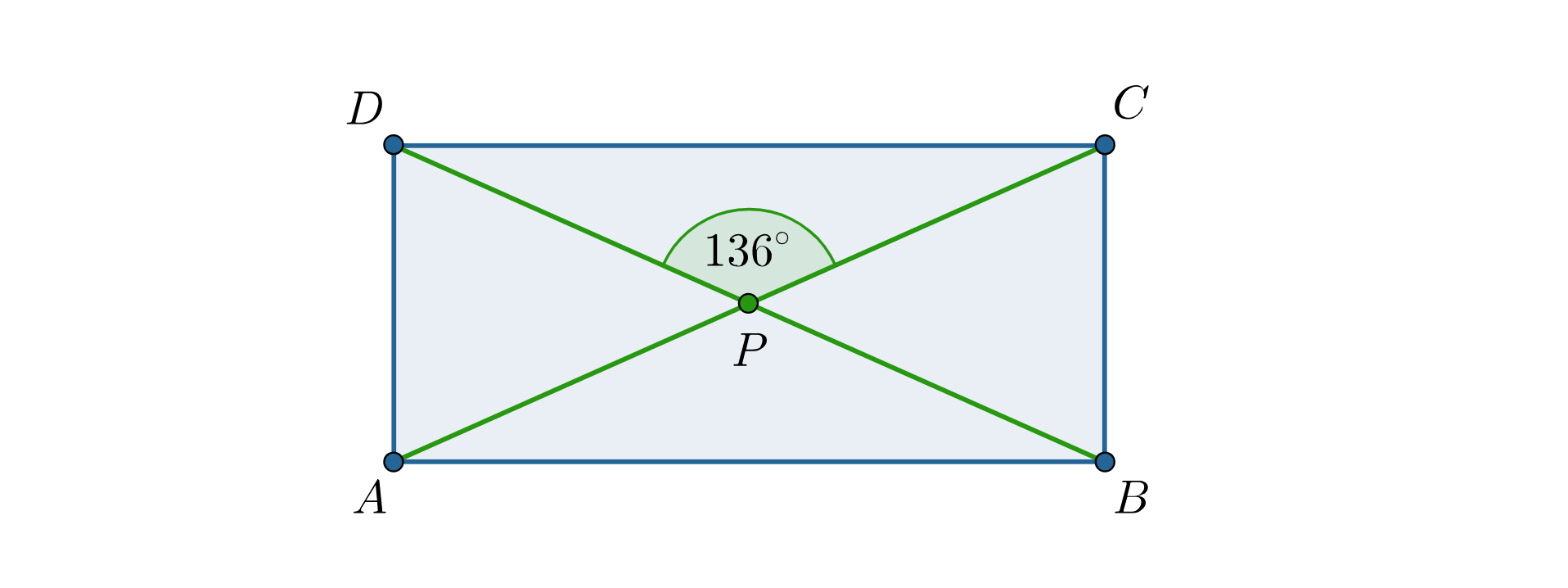
Przekątne prostokąta ABCD przecinają się w punkcie P pod kątem 136°.

R1cf5rm8cSw4V1
Grafika przedstawiająca prostokąt opisany w treści zadania.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RkK4GS6y7kkIK
Uzupełnij rosnąco miary kątów trójkąta BPC wpisując liczby w puste pola. Odpowiedź: Miary kątów trójkąta BPC wynoszą Tu uzupełnij°, Tu uzupełnij°, Tu uzupełnij°
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 17
RPEOT9BXJ8Wps
Narysowano pewien kwadrat, a następnie dorysowano na zewnątrz kwadratu cztery trójkąty równoboczne tak, aby każdy bok kwadratu był równocześnie bokiem jednego z trójkątów. Dokończ zdania i uzupełnij puste pola. Nazwa wielokąta utworzonego przez kwadrat i wszystkie trójkąty to Tu uzupełnij.Suma miar kątów wewnętrznych utworzonego wielokąta to Tu uzupełnij°.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Notatnik

Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.

R1b8OvSPUG8s3
(Uzupełnij).
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
7. Trapez i jego rodzaje
9. Koła i okręgi