1. Pole figury. Jednostki pola

R4MPJUMZitjX2

Pola uprawne widziane z samolotu lecącego na niewielkiej wysokości wyglądają bardzo geometrycznie.

REQgVy2IP9RWH1

Rysunek pola uprawnego widzianego z samolotu. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Na zdjęciu widzimy, jak można dzielić figury płaskie w sposób nieregularny.
My zaczniemy od podziału figury na kwadraty.

Ciekawostka

W osiemnastowiecznej Polsce stosowano inne miary pola niż obecnie. Na przykład jednostkami miar powierzchni stosowanymi dla gruntów rolnych były:

kopanka – $19, 95 m^{2}$ ,
laska kwadratowa – $4$ kopanki,
kwadratowy pręt większy – $2, 5$ laski kwadratowej,
wertel – $18$ kwadratowych prętów większych,
morga – $1 \frac{2}{3}$ wertela – $5 985 m^{2}$ .

Kmiecie, którzy stanowili w owym czasie największą grupę mieszkańców wsi, posiadali najczęściej dziewięćdziesięciomorgowe gospodarstwo.

Pole figury

Wiemy już, że pole figury to nieujemna liczba określająca, ile figur jednostkowych (lub ich części) mieści się w danej figurze.

R1czLfMHqANhY1

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Pole figury może przyjmować różne wartości liczbowe w zależności od tego, jaką figurę przyjmiemy za jednostkę miary.

Przykład 1

RkGTdtoUCrmw71

Przykład 2

Pole prostokąta $A B C D$ jest równe $18$ , gdy za jednostkę pola przyjmiemy kwadrat.

R1Y9wfC2F60Ym1

Rysunek prostokąta A B C D o wymiarach sześć kratek na trzy kratki. Prostokąt złożony jest z osiemnastu kwadratów. Zapis: Pole A B C D =18. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Określ przybliżone pole tego prostokąta, przyjmując za jednostkę pola figurę wyróżnioną kolorem zielonym.

RfqPiirq16wl61

Na rysunku widać trzy figury: figura a to prostokąt złożony z dwóch kratek, figura b to trójkąt, który stanowi połowę jednej kratki, figura c to trapez złożony z jednej całej kratki i trójkąta, który stanowi połowę kratki. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Odpowiedź:

$9$
$36$
$12$

Przykład 3

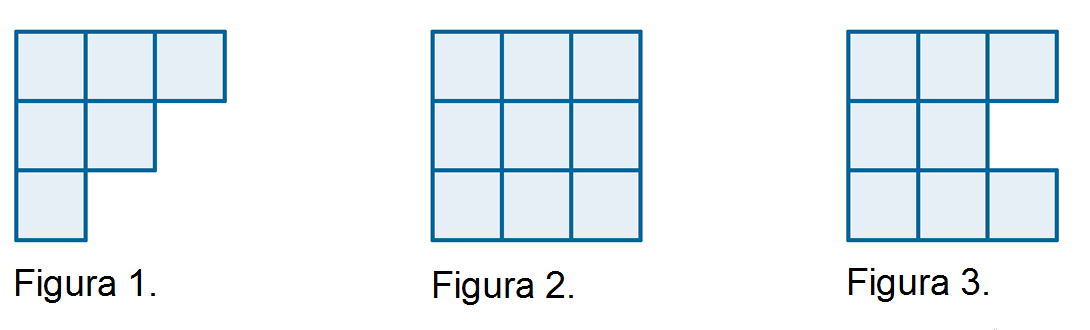
Do zbudowania każdej z figur użyto tych samych trzech prostokątów $K$ , $L$ , $M$ .
Czy pola tych figur są równe? Jeśli nie, to która z nich ma największe, a która najmniejsze pole? Dlaczego?

RKWnaUbQBpM3T1

Jednostki pola

Zapamiętaj!

$1 m^{2}$ to kwadrat o boku $1 m$ .

Inne najczęściej używane jednostki pola to: ${mm}^{2}$ , ${cm}^{2}$ , ${dm}^{2}$ , ${km}^{2}$ .

$1 {mm}^{2}$
$1 {cm}^{2} = 100 {mm}^{2}$
$1 {dm}^{2} = 100 {cm}^{2} = 10 000 {mm}^{2}$
$1 m^{2} = 100 {dm}^{2} = 10 000 {cm}^{2}$
$1 {km}^{2} = 1 000 000 m^{2}$

Rji1qeiJLKdtj1

Przykład 4

Pole powierzchni dywanu jest równe $5, 6 m^{2}$ . Ile to ${dm}^{2}$ ? Ile to ${cm}^{2}$ ?

$1 m^{2}$ to $100 {dm}^{2}$ , więc $5, 6 m^{2} = 5, 6 \cdot 100 {dm}^{2} = 560 {dm}^{2}$ .

$1 m^{2}$ to $10 000 {cm}^{2}$ , więc $5, 6 m^{2} = 5, 6 \cdot 10 000 {cm}^{2} = 56 000 {cm}^{2}$ .

Przykład 5

Jedna z największych polskich sal kinowych znajduje się w Warszawie w centrum handlowym Złote Tarasy. Ekran w tej sali ma wymiary $2900 c m$ i $1200 c m$ .

Jeden z największych ekranów kinowych na świecie znajduje się w Sydney w Australii i ma wymiary $2970 c m$ i $3570 c m$ .

Przyjmij, że ekrany kinowe są prostokątami i oblicz, o ile ${dm}^{2}$ pole ekranu w Sydney jest większe od pola ekranu w Warszawie.

Obliczamy pole powierzchni ekranu w warszawskich Złotych Tarasach w centymetrach kwadratowych i otrzymany wynik zapisujemy w decymetrach kwadratowych.

P_{W} = 2 900 \cdot 1 200

P_{W} = 3 480 000 {cm}^{2}

1 {dm}^{2} = 100 {cm}^{2}

, więc

1 {cm}^{2} = 0, 01 {dm}^{2}

P_{W} = 3 480 000 \cdot 0, 01 {dm}^{2} = 34 800 {dm}^{2}

Obliczamy pole powierzchni ekranu znajdującego się w Sydney w centymetrach kwadratowych i otrzymany wynik zapisujemy w decymetrach kwadratowych.

P_{S} = 2 970 \cdot 3 570

P_{S} = 10 602 900 {cm}^{2}

P_{S} = 10 602 900 \cdot 0, 01 {dm}^{2} = 106 029 {dm}^{2}

Wyznaczamy różnicę pól.

P_{S} - P_{W} = 106 029 {dm}^{2} - 34 800 {dm}^{2} = 71 229 {dm}^{2}

Pole powierzchni ekranu w Sydney jest o $71 299 {dm}^{2}$ większe od pola powierzchni ekranu w Warszawie.

Jednostki pola powierzchni gruntów

Jednostki często używane do wyznaczania pól powierzchni gruntów rolnych, działek budowlanych itp. to ar i hektar.

Zapamiętaj!

$1 ar (1 a)$ to kwadrat o boku długości $10 m$ .

1 a = 10 m \cdot 10 m = 100 m^{2}

$1$ hektar $(1 ha)$ to kwadrat o boku długości $100 m$ .

1 ha = 100 m \cdot 100 m = 10 000 m^{2}

Zapamiętaj!

$1 a = 100 m^{2}$
$1 ha = 10 000 m^{2}$
$1 ha = 100 a$

Przykład 6

Boisko na Stadionie Narodowym w Warszawie ma wymiary $105 m$ i $68 m$ . Ile to hektarów? Ile to arów?

Obliczamy pole powierzchni boiska w metrach kwadratowych.

P = 105 \cdot 68 = 7 140

P = 7 140 m^{2}

Zapisujemy wynik w hektarach.

1 ha = 10 000 m^{2}

zatem

1 m^{2} = 0, 0001 ha

P = 7 140 \cdot 0, 0001 ha = 0, 7140 ha

Zapisujemy pole powierzchni boiska w arach.

1 a = 100 m^{2}

1 m^{2} = 0, 01 a

P = 7 140 \cdot 0, 01 a = 71, 40 a

Odpowiedź: Boisko na Stadionie Narodowym ma pole powierzchni równe $0, 7140 ha$ , czyli $71, 4 a$ .

Ważne!

Aby dobrze zamieniać jednostki pola, trzeba wiedzieć, ile mniejszych jednostek mieści się w większej.

1 {cm}^{2} = 100 {mm}^{2}

1 a = 100 m^{2}

1 {dm}^{2} = 100 {cm}^{2}

1 ha = 100 a

1 m^{2} = 100 {dm}^{2}

1 {km}^{2} = 100 ha

Ważne!

Mówimy, że jeden centymetr kwadratowy to jedna setna decymetra kwadratowego.

1 {cm}^{2} = 0,01 {dm}^{2}

Podobnie

1 {mm}^{2} = 0,01 {cm}^{2}

1 {dm}^{2} = 0,01 m^{2}

1 a = 0,01 ha

1 m^{2} = 0,01 a

1 ha = 0,01 {km}^{2}

Ćwiczenie 1

Figury przedstawione na rysunkach zbudowane są z jednakowych kwadratów.

RjXN7WbXkgOtn1

Rysunek czterech różnych figur zbudowanych z jednakowych kwadratów. Figura A zbudowana jest z siedmiu kwadratów, figura B zbudowana jest z dziewięciu kwadratów, figura C zbudowana jest z siedmiu kwadratów i figura D zbudowana jest z siedmiu kwadratów. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RcDbcutUQvC3s

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 2

Dwie figury o takim samym kształcie ułożono z dwóch rodzajów kwadratowych klocków. Bok mniejszego klocka jest dwa razy krótszy niż bok większego. Czy obie figury mają jednakowe pole?

R1QTv1LPNAxsO

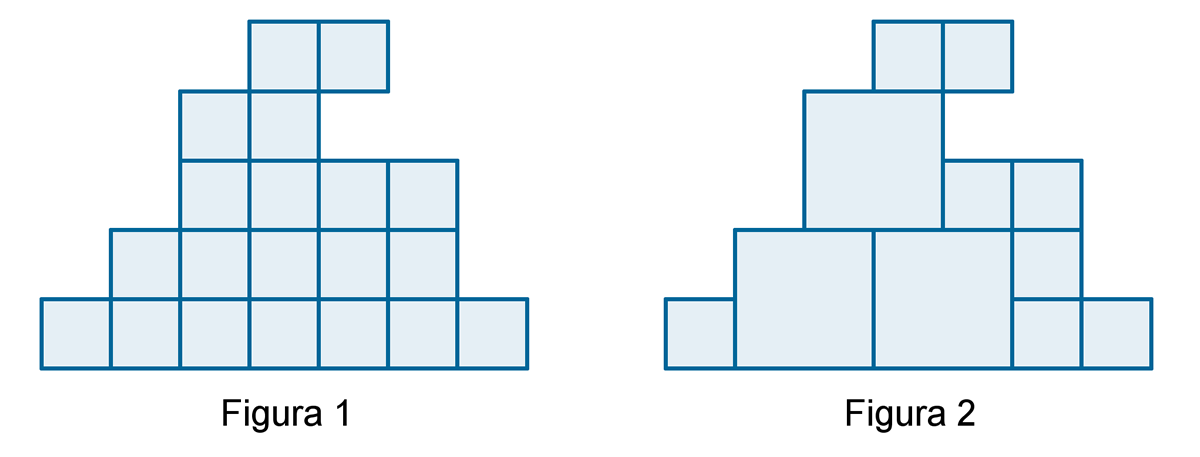
Na obrazku widać dwie figury. Figura 1 składa się z dwudziestu jednakowych małych kwadratów, a figura 2 składa się z trzech większych kwadratów i z ośmiu mniejszych kwadratów. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1TgCedJgbSkv

Uzupełnij zdania, przeciągając w luki odpowiednie wyrażenia lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. 1. druga figura może być ułożona z

20

małych klocków jak figura pierwsza., 2. pole figury drugiej jest o

9

mniejsze niż pierwszej., 3. Nie, 4. Tak, 5. pierwsza figura jest ułożona z

20

klocków, a druga figura z

11

klocków, ponieważ 1. druga figura może być ułożona z

20

małych klocków jak figura pierwsza., 2. pole figury drugiej jest o

9

mniejsze niż pierwszej., 3. Nie, 4. Tak, 5. pierwsza figura jest ułożona z

20

klocków, a druga figura z

11

klocków

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 3

Figury przestawione na rysunkach ułożone są z jednakowych kwadratowych klocków.

Rm9HPAHiMvDtw

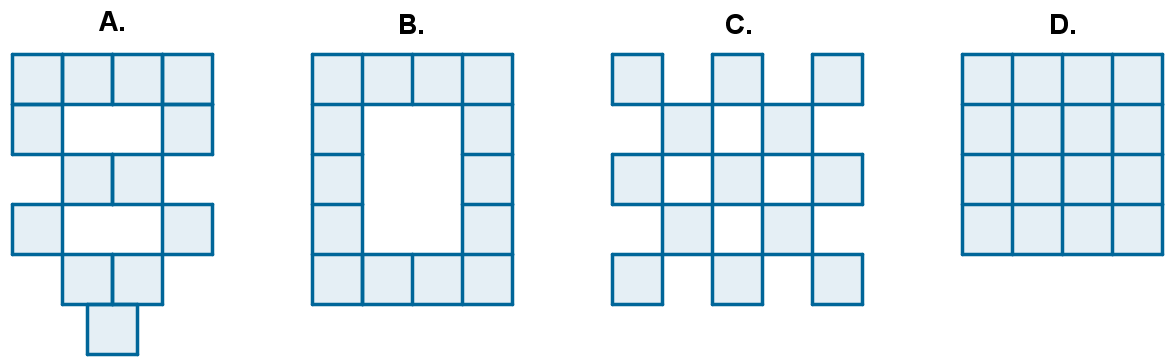
Na rysunku widać cztery figury. Figura A składa się z trzynastu jednakowych kwadratów, figura B składa się z czternastu jednakowych kwadratów, figura C składa się z trzynastu jednakowych kwadratów i figura D składa się z szesnastu jednakowych kwadratów. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R16gOPqZEURKu

Uzupełnij zdania, przeciągając w luki odpowiednie liczby i litery lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. Największe pole ma figura 1.

C

D

, 2.

55

, 3.

B

C

, 4.

C

, 5.

A

, 6.

A

D

, 7.

57

, 8.

56

, 9.

46

, 10.

A

C

, 11.

D

, 12.

B

, 13.

A

B

.Figury 1.

C

D

, 2.

55

, 3.

B

C

, 4.

C

, 5.

A

, 6.

A

D

, 7.

57

, 8.

56

, 9.

46

, 10.

A

C

, 11.

D

, 12.

B

, 13.

A

B

mają jednakowe pola.Do ułożenia wszystkich figur wykorzystano łącznie 1.

C

D

, 2.

55

, 3.

B

C

, 4.

C

, 5.

A

, 6.

A

D

, 7.

57

, 8.

56

, 9.

46

, 10.

A

C

, 11.

D

, 12.

B

, 13.

A

B

klocków.

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 4

Wszystkie figury zbudowane są z kwadratów o boku długości $1 cm$ .

Ra2YZy7Pu5PTS

Na rysunku widać trzy figury. Pierwsza figura składa się z sześciu kwadratów, druga figura składa się z dziewięciu kwadratów, a trzecia figura składa się z ośmiu kwadratów. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1QAJIt1XLyzm

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 5

Narysuj kredą na podłodze kwadrat o polu $1 m^{2}$ . Warto sprawdzić, ile osób może równocześnie stanąć na tym kwadracie.

Rc2oJ6WmVfWIx1

Ćwiczenie 6

Uzupełnij zdania, przeciągając w luki odpowiednie liczby i jednostki lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. Pole kwadratu o boku długości

10 m

wynosi 1.

1000

, 2.

a

, 3.

km

, 4.

ha

, 5.

100

, 6.

10000

m^{2}

. Pole tego kwadratu, to

1

1000

, 2.

a

, 3.

km

, 4.

ha

, 5.

100

, 6.

10000

.Pole kwadratu o boku długości

100 m

wynosi 1.

1000

, 2.

a

, 3.

km

, 4.

ha

, 5.

100

, 6.

10000

m^{2}

. Pole tego kwadratu, to

1

1000

, 2.

a

, 3.

km

, 4.

ha

, 5.

100

, 6.

10000

Przeciągnij i upuść.

$100$ , $10 000$ , $1 000$ , $a$ , $h a$

a) Pole kwadratu o boku długości $10 m$ wynosi ............ $m^{2}$ . Pole tego kwadratu, to $1$ ............
b) Pole kwadratu o boku długości $100 m$ wynosi ............ $m^{2}$ . Pole tego kwadratu, to $1$ ............

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1D5qlm8QpcDZ

Ćwiczenie 7

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R14DTdabJ5hbv

Ćwiczenie 8

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1D5labG66WWN

Ćwiczenie 9

Uzupełnij odpowiedzi na poniższe pytania, wpisując w luki odpowiednie liczby. Iloma kwadratami o polu

1 {mm}^{2}

można wyłożyć kwadrat o polu

1 {dm}^{2}

? Odpowiedź: Tu uzupełnij Iloma kwadratami o polu

1 {cm}^{2}

można wyłożyć kwadrat o polu

1 m^{2}

? Odpowiedź: Tu uzupełnij Iloma kwadratami o polu

1 {dm}^{2}

można wyłożyć kwadrat o polu

1 a

? Odpowiedź: Tu uzupełnij Iloma kwadratami o polu

1 m^{2}

można wyłożyć kwadrat o polu

1 ha

? Odpowiedź: Tu uzupełnij Iloma kwadratami o polu

1 a

można wyłożyć kwadrat o polu

1 {km}^{2}

? Odpowiedź: Tu uzupełnij

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Rbu2Sv2AwK14n

Ćwiczenie 10

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1Et90AUseQZc

Ćwiczenie 11

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1RJTkN55wIs01

Ćwiczenie 12

Uzupełnij równości, przeciągając w luki odpowiednie liczby i jednostki lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej.

1 {km}^{2} = 100

400000

, 2.

200000

, 3.

10000

, 4.

m^{2}

, 5.

1500000

, 6.

{dm}^{2}

, 7.

20000

, 8.

100000

, 9.

1000

, 10.

a

, 11.

150000

, 12.

ha

, 13.

4000000

= 10000

400000

, 2.

200000

, 3.

10000

, 4.

m^{2}

, 5.

1500000

, 6.

{dm}^{2}

, 7.

20000

, 8.

100000

, 9.

1000

, 10.

a

, 11.

150000

, 12.

ha

, 13.

4000000

= 1000000

400000

, 2.

200000

, 3.

10000

, 4.

m^{2}

, 5.

1500000

, 6.

{dm}^{2}

, 7.

20000

, 8.

100000

, 9.

1000

, 10.

a

, 11.

150000

, 12.

ha

, 13.

4000000

= 100000000

400000

, 2.

200000

, 3.

10000

, 4.

m^{2}

, 5.

1500000

, 6.

{dm}^{2}

, 7.

20000

, 8.

100000

, 9.

1000

, 10.

a

, 11.

150000

, 12.

ha

, 13.

4000000

10 ha =

400000

, 2.

200000

, 3.

10000

, 4.

m^{2}

, 5.

1500000

, 6.

{dm}^{2}

, 7.

20000

, 8.

100000

, 9.

1000

, 10.

a

, 11.

150000

, 12.

ha

, 13.

4000000

a

100 a =

400000

, 2.

200000

, 3.

10000

, 4.

m^{2}

, 5.

1500000

, 6.

{dm}^{2}

, 7.

20000

, 8.

100000

, 9.

1000

, 10.

a

, 11.

150000

, 12.

ha

, 13.

4000000

m^{2}

1000 m^{2} =

400000

, 2.

200000

, 3.

10000

, 4.

m^{2}

, 5.

1500000

, 6.

{dm}^{2}

, 7.

20000

, 8.

100000

, 9.

1000

, 10.

a

, 11.

150000

, 12.

ha

, 13.

4000000

{dm}^{2}

20 {km}^{2} =

400000

, 2.

200000

, 3.

10000

, 4.

m^{2}

, 5.

1500000

, 6.

{dm}^{2}

, 7.

20000

, 8.

100000

, 9.

1000

, 10.

a

, 11.

150000

, 12.

ha

, 13.

4000000

a

40 ha =

400000

, 2.

200000

, 3.

10000

, 4.

m^{2}

, 5.

1500000

, 6.

{dm}^{2}

, 7.

20000

, 8.

100000

, 9.

1000

, 10.

a

, 11.

150000

, 12.

ha

, 13.

4000000

m^{2}

15 a =

400000

, 2.

200000

, 3.

10000

, 4.

m^{2}

, 5.

1500000

, 6.

{dm}^{2}

, 7.

20000

, 8.

100000

, 9.

1000

, 10.

a

, 11.

150000

, 12.

ha

, 13.

4000000

{dm}^{2}

Przeciągnij i upuść.

$400 000$ , $m^{2}$ , $200 000$ , $1 500 000$ , ${dm}^{2}$ , $4 000 000$ , $20 000$ , $10 000$ , $1 000$ , $100 000$ , $ha$ , $a$ , $150 000$

$1 {km}^{2} = 100$ .................. $= 10 000$ .................. $= 1 000 000$ .................. $= 100 000 000$ ..................

a) $10 ha =$ .................. $a$ ; b) $100 a =$ .................. $m^{2}$ ; c) $1 000 m^{2} =$ .................. ${dm}^{2}$ ;
d) $20 {km}^{2} =$ .................. $a$ ; e) $40 ha =$ .................. $m^{2}$ ; f) $15 a =$ .................. ${dm}^{2}$ ;

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 13

W kwadracie o polu $1 {dm}^{2}$ narysowano trzy figury (każda w innym kolorze). Jakie pole ma figura niebieska, jakie zielona, a jakie pomarańczowa? Jaką częścią kwadratu o polu $1 {dm}^{2}$ jest każda z kolorowych figur?

RKoMEzGbqVLCO1

Rysunek kwadratu o polu 1 decymetra kwadratowego podzielonego na sto jednakowych kwadratów jednostkowych. Wewnątrz zaznaczone trzy figury. Figura zielona zbudowana z 24 kwadratów jednostkowych. Figura niebieska zbudowana z 17 kwadratów jednostkowych. Figura żółta zbudowana z 22 kwadratów jednostkowych. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RAjU78MTK24Kf

Uzupełnij poniższe odpowiedzi, wpisując w luki odpowiednie liczby. Pole niebieskiej figury wynosi Tu uzupełnij

{cm}^{2}

, pole pomarańczowej figury wynosi Tu uzupełnij

{cm}^{2}

, a pole zielonej figury wynosi Tu uzupełnij

{cm}^{2}

. Niebieska figura to Tu uzupełnij kwadratu o polu jednego decymetra kwadratowego, pomarańczowa figura to Tu uzupełnij kwadratu o polu jednego decymetra kwadratowego, a zielona figura to Tu uzupełnij kwadratu o polu jednego decymetra kwadratowego.

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RXy90fPHy6Ogp

Ćwiczenie 14

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RQfnjXk5mgzGQ1

Ćwiczenie 15

Uzupełnij równości, przeciągając w luki odpowiednie liczby i jednostki lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej.

1000000 {mm}^{2} = 10000

0, 01

, 2.

{dm}^{2}

, 3.

0, 4

, 4.

0, 1

, 5.

{cm}^{2}

, 6.

ha

, 7.

0, 2

, 8.

m^{2}

, 9.

a

, 10.

10

, 11.

0, 15

, 12.

0, 02

, 13.

0, 04

, 14.

0, 001

= 100

0, 01

, 2.

{dm}^{2}

, 3.

0, 4

, 4.

0, 1

, 5.

{cm}^{2}

, 6.

ha

, 7.

0, 2

, 8.

m^{2}

, 9.

a

, 10.

10

, 11.

0, 15

, 12.

0, 02

, 13.

0, 04

, 14.

0, 001

= 1

0, 01

, 2.

{dm}^{2}

, 3.

0, 4

, 4.

0, 1

, 5.

{cm}^{2}

, 6.

ha

, 7.

0, 2

, 8.

m^{2}

, 9.

a

, 10.

10

, 11.

0, 15

, 12.

0, 02

, 13.

0, 04

, 14.

0, 001

= 0, 01

0, 01

, 2.

{dm}^{2}

, 3.

0, 4

, 4.

0, 1

, 5.

{cm}^{2}

, 6.

ha

, 7.

0, 2

, 8.

m^{2}

, 9.

a

, 10.

10

, 11.

0, 15

, 12.

0, 02

, 13.

0, 04

, 14.

0, 001

= 0, 0001

0, 01

, 2.

{dm}^{2}

, 3.

0, 4

, 4.

0, 1

, 5.

{cm}^{2}

, 6.

ha

, 7.

0, 2

, 8.

m^{2}

, 9.

a

, 10.

10

, 11.

0, 15

, 12.

0, 02

, 13.

0, 04

, 14.

0, 001

1000 {mm}^{2} =

0, 01

, 2.

{dm}^{2}

, 3.

0, 4

, 4.

0, 1

, 5.

{cm}^{2}

, 6.

ha

, 7.

0, 2

, 8.

m^{2}

, 9.

a

, 10.

10

, 11.

0, 15

, 12.

0, 02

, 13.

0, 04

, 14.

0, 001

{cm}^{2}

10 {cm}^{2} =

0, 01

, 2.

{dm}^{2}

, 3.

0, 4

, 4.

0, 1

, 5.

{cm}^{2}

, 6.

ha

, 7.

0, 2

, 8.

m^{2}

, 9.

a

, 10.

10

, 11.

0, 15

, 12.

0, 02

, 13.

0, 04

, 14.

0, 001

{dm}^{2}

1 {dm}^{2} =

0, 01

, 2.

{dm}^{2}

, 3.

0, 4

, 4.

0, 1

, 5.

{cm}^{2}

, 6.

ha

, 7.

0, 2

, 8.

m^{2}

, 9.

a

, 10.

10

, 11.

0, 15

, 12.

0, 02

, 13.

0, 04

, 14.

0, 001

m^{2}

20 m^{2} =

0, 01

, 2.

{dm}^{2}

, 3.

0, 4

, 4.

0, 1

, 5.

{cm}^{2}

, 6.

ha

, 7.

0, 2

, 8.

m^{2}

, 9.

a

, 10.

10

, 11.

0, 15

, 12.

0, 02

, 13.

0, 04

, 14.

0, 001

a

40 a =

0, 01

, 2.

{dm}^{2}

, 3.

0, 4

, 4.

0, 1

, 5.

{cm}^{2}

, 6.

ha

, 7.

0, 2

, 8.

m^{2}

, 9.

a

, 10.

10

, 11.

0, 15

, 12.

0, 02

, 13.

0, 04

, 14.

0, 001

ha

15 ha =

0, 01

, 2.

{dm}^{2}

, 3.

0, 4

, 4.

0, 1

, 5.

{cm}^{2}

, 6.

ha

, 7.

0, 2

, 8.

m^{2}

, 9.

a

, 10.

10

, 11.

0, 15

, 12.

0, 02

, 13.

0, 04

, 14.

0, 001

{km}^{2}

Przeciągnij i upuść.

${cm}^{2}$ , $0, 1$ , $0, 001$ , $0, 15$ , $ha$ , $0, 4$ , $0, 04$ , $0, 2$ , $10$ , $0, 01$ , $a$ , $0, 02$ , ${dm}^{2}$ , $m^{2}$

$1 000 000 {mm}^{2} = 10 000$ ............ $= 100$ ............ $= 1$ ............ $= 0, 01$ ............ $= 0, 0001$ ............
a) $1 000 {mm}^{2} =$ ............ ${cm}^{2}$ ; b) $10 {cm}^{2} =$ ............ ${dm}^{2}$ ; c) $1 {dm}^{2} =$ ............ $m^{2}$ ;
d) $20 m^{2} =$ ............ $a$ ; e) $40 a =$ ............ $ha$ ; f) $15 ha =$ ............ ${km}^{2}$ ;

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RWjLurEEi6uNo

Ćwiczenie 16

Uzupełnij wyrażenia, przeciągając w luki odpowiednie znaki lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej.

612 {dm}^{2}

\neq

, 2.

=

, 3.

=

, 4.

\neq

, 5.

=

, 6.

\neq

, 7.

\neq

, 8.

=

, 9.

\neq

, 10.

=

, 11.

\neq

, 12.

=

0, 612 m^{2}

350 {dm}^{2}

\neq

, 2.

=

, 3.

=

, 4.

\neq

, 5.

=

, 6.

\neq

, 7.

\neq

, 8.

=

, 9.

\neq

, 10.

=

, 11.

\neq

, 12.

=

0, 035 a

30 {cm}^{2}

\neq

, 2.

=

, 3.

=

, 4.

\neq

, 5.

=

, 6.

\neq

, 7.

\neq

, 8.

=

, 9.

\neq

, 10.

=

, 11.

\neq

, 12.

=

0, 00003 a

50 a

\neq

, 2.

=

, 3.

=

, 4.

\neq

, 5.

=

, 6.

\neq

, 7.

\neq

, 8.

=

, 9.

\neq

, 10.

=

, 11.

\neq

, 12.

=

0, 05 ha

999, 9 {dm}^{2}

\neq

, 2.

=

, 3.

=

, 4.

\neq

, 5.

=

, 6.

\neq

, 7.

\neq

, 8.

=

, 9.

\neq

, 10.

=

, 11.

\neq

, 12.

=

0, 09999 a

1005 {dm}^{2}

\neq

, 2.

=

, 3.

=

, 4.

\neq

, 5.

=

, 6.

\neq

, 7.

\neq

, 8.

=

, 9.

\neq

, 10.

=

, 11.

\neq

, 12.

=

0, 01005 ha

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 17

Przyjmij za jednostkę pola kratkę zeszytową i narysuj figurę o polu

równym $7$ ,
mniejszym od $5$ ,
większym od $10$ .

RVxyAYQ10uZs3

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Przyjmij za jednostkę pola kratkę zeszytową i zastanów się z ilu kratek mogą składać się figury o polu

równym $7$ ,
mniejszym od $5$ ,
większym od $10$ .

Jedna kratka w zeszycie ma pole równe $1$ .

R7eCLMH0oiWBW

Ćwiczenie 18

Uzupełnij.

a) $2 m^{2} =$ ............ ${cm}^{2}$
b) $16, 5 m^{2} =$ ............ ${cm}^{2}$
c) $11 {dm}^{2} =$ ............ ${cm}^{2}$
d) $150 {mm}^{2} =$ ............ ${cm}^{2}$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RmwJFVPgSWDCx

Ćwiczenie 19

Uzupełnij.

a) $5 {km}^{2} =$ .............. $m^{2}$
b) $182 {cm}^{2} =$ ............ ${dm}^{2}$
c) $4444 {cm}^{2} =$ ............ $m^{2}$
d) $7890000 {cm}^{2} =$ ............ $m^{2}$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 20

Na planie wykonanym w skali $1 : 2 000$ pole powierzchni parku jest równe $4 {cm}^{2}$ . Jakie pole powierzchni ma ten park w rzeczywistości?

RbbnLx8y8ZZ6S

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Na planie $1 cm$ odpowiada $2000 cm$ w rzeczywistości, więc $1 {cm}^{2}$ na planie odpowiada $4 000 000 {cm}^{2}$ w rzeczywistości.

Pole powierzchni parku jest równe $1600 m^{2}$ .

Ćwiczenie 21

R1aQb5dGsaRT4

Marcin
Agata
Bogdan
Emilia

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Aby porównać powierzchnie trawników, należy ich pola zapisać w takiej samej jednostce, na przykład w $m^{2}$ . Trawnik Emilii jest największy.

Ćwiczenie 22

R186frIEUhhBm

$150 a$
$150 \cdot 1 0^{2} m^{2}$
$150 \cdot 1 0^{5} c m^{2}$
$150 \cdot 1 0^{2} a$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Należy zamienić $2 ha$ na $ary$ oraz na $m^{2}$ i ${cm}^{2}$ .

1 a = 100 m^{2}

1 ha = 10 000 m^{2}

1 ha = 100 a

1 m^{2} = 10 000 {cm}^{2}

R1Q0PvLLAjpJL

Ćwiczenie 23

Połącz w pary.

$7, 3 ha$
$0, 073 ha$
$73 a$
$0, 73 a$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 24

Uruchom poniższy aplet i wykonaj polecenia.

RrctS8pYolpsB1

RYiR4kgTyQIFZ

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 25

Uruchom poniższy aplet i wykonaj polecenia.

RW5ZRZgY7XJ9a1

RAU3BCmRaS9N6

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 26

Uruchom poniższy aplet i wykonaj polecenia.

RTUYhLVFiQ60v1

R1NpsukexjHFj

Przeciągnij i upuść odpowiednie wymiary prostokątów. Prostokąt o polu równym

15 {cm}^{2}

ma wymiary 1.

4 cm \times 1 cm

, 2.

4 cm \times 5 cm

, 3.

1 cm \times 6 cm

, 4.

2 cm \times 4 cm

, 5.

3 cm \times 5 cm

, 6.

2 cm \times 3 cm

, 7.

7 cm \times 8 cm

, 8.

7 cm \times 6 cm

.Prostokąt o polu równym

56 {cm}^{2}

ma wymiary 1.

4 cm \times 1 cm

, 2.

4 cm \times 5 cm

, 3.

1 cm \times 6 cm

, 4.

2 cm \times 4 cm

, 5.

3 cm \times 5 cm

, 6.

2 cm \times 3 cm

, 7.

7 cm \times 8 cm

, 8.

7 cm \times 6 cm

.Prostokąt o polu równym

4 {cm}^{2}

ma wymiary 1.

4 cm \times 1 cm

, 2.

4 cm \times 5 cm

, 3.

1 cm \times 6 cm

, 4.

2 cm \times 4 cm

, 5.

3 cm \times 5 cm

, 6.

2 cm \times 3 cm

, 7.

7 cm \times 8 cm

, 8.

7 cm \times 6 cm

.Prostokąt o polu równym

8 {cm}^{2}

ma wymiary 1.

4 cm \times 1 cm

, 2.

4 cm \times 5 cm

, 3.

1 cm \times 6 cm

, 4.

2 cm \times 4 cm

, 5.

3 cm \times 5 cm

, 6.

2 cm \times 3 cm

, 7.

7 cm \times 8 cm

, 8.

7 cm \times 6 cm

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 27

Uruchom poniższy aplet i wykonaj polecenia.

RKUUUXoGRzoKb1

R1Mf8BCc6ebKt

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 28

Uruchom poniższy aplet i wykonaj polecenia.

R1IOsWN8c3PHs1

ROnHIGTjCAQOr

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 29

RBB6LzXfpTxmA

Oblicz pole figury, przyjmując za jednostkę pola podany wielokąt. Uzupełnij poniższe zdania, wpisując w luki odpowiednie liczby. Pole prostokąta składającego się z

20

kratek, przyjmując za jednostkę pola trójkąt, który stanowi połowę kratki, wynosi Tu uzupełnij.Pole kwadratu składającego się z

9

kratek, przyjmując za jednostkę pola prostokąt złożony z dwóch kratek, wynosi Tu uzupełnij.Pole prostokąta składającego się z

15

kratek, przyjmując za jednostkę pola trapez złożony z jednej kratki i trójkąta, który stanowi połowę kratki, wynosi Tu uzupełnij.

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Oblicz pole figury, przyjmując za jednostkę pola wielokąt wyróżniony kolorem zielonym. Wyniki wpisz w poniższe pola.

R1CFipYWCwRnS1

Rysunek trzech figur zbudowanych z trójkątów, kwadratów i prostokątów. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R13OKSG50w7fz

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Notatnik

Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.

R1b8OvSPUG8s3

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

2. Pole prostokąta i kwadratu

Pola wielokątów