1. Proste doświadczenia losowe

R1TlsySrWzt59

RjraU8MJC48X11

Na grafice ukazany jest Jakob Bernoulli. To mężczyzna z ciemnymi, kręconymi włosami. Na sobie ma czarny płaszcz i biały żabot. — Źródło: dostępny w internecie: Wikipedia.org, domena publiczna.

Jacob Bernoulli to siedemnastowieczny szwajcarski matematyk.

W swojej pracy Ars Conjectandi (Sztuka przewidywania) opublikowanej w $1713$ roku, przedstawia eksperymenty, w którym można otrzymać tylko dwa wyniki, zwane sukcesem lub porażką. Przykładem takiego eksperymentu (obecnie zwanego próbą Bernoulliego) może być rzut monetą – można otrzymać tylko orła lub reszkę.

R18QoHbQaOlir1

Na ilustracji ukazany jest dokument związany z Jakobem Bernoullim. — Źródło: dostępny w internecie: Wikipedia.org, domena publiczna.

Rozważania Bernoulliego uważane są za przełomowe dla rozwoju rachunku prawdopodobieństwa.

W tym materiale będziemy również rozpatrywać pewne eksperymenty, ale głównie takie, które mają więcej niż dwa wyniki.

Doświadczenie losowe

Rzut sześcienną kostką do gry, wyciągnięcie karty z talii kart, losowanie pytania na egzaminie, rzut dwiema monetami – to przykłady eksperymentów, które można wielokrotnie powtarzać w takich samych lub zbliżonych warunkach, a których wyników nie jesteśmy w stanie przewidzieć. Takie eksperymenty nazywamy w matematyce doświadczeniami losowymiDoświadczenie losowedoświadczeniami losowymi.

Wynika stąd, że na przykład otrzymanie przez Urszulę piątki z klasówki z matematyki nie jest doświadczeniem losowym, gdyż ocena zależy od umiejętności dziewczynki, a nie od przypadku.

W doświadczeniu losowym znamy wszystkie możliwe wyniki. Przy czym zakładamy, że doświadczenie losowe ma więcej niż jeden możliwy wynik. Na przykład w jednokrotnym rzucie monetą są dwa możliwe wyniki: otrzymanie orła lub reszki.

Pojedynczy wynik doświadczenia losowego to zdarzenie elementarneZdarzenie elementarnezdarzenie elementarne.

Każdy zbiór zdarzeń elementarnych spełniających określony warunek nazywamy zdarzeniem losowymZdarzenie losowezdarzeniem losowym.

RSTJR5Mcjeo91

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Przykład 1

Przykłady doświadczeń losowych i zdarzeń losowych w tych doświadczeniach.

Doświadczenie losowe	Przykłady zdarzenia losowego
Rzut dwiema monetami.	Wypadnięcie dwóch orłów.
Rzut sześcienną kostką do gry.	Wyrzucenie liczby oczek podzielnej przez trzy.
Losowanie karty z talii $52$ kart do gry.	Wylosowanie damy lub króla.
Losowanie jednej kuli z pudełka zawierającego dwie kule białe, trzy czarne i kulę złotą.	Wylosowanie kuli, która nie jest biała.

Zdarzenia losowe oznaczamy dużymi literami: $A$ , $B$ , $C$ , $\dots$

Zdarzenia elementarne

W doświadczeniu losowym zakładamy, że każdy poszczególny wynik doświadczenia jest rozłączny z pozostałymi. Te najprostsze wyniki nazywamy zdarzeniami elementarnymi.

Przykład 2

W tabelce zawarte są przykłady doświadczeń losowych i zdarzeń elementarnych w tych doświadczeniach.

Doświadczenie losowe	Zdarzenie elementarne
Rzut monetą.	Wyrzucenie orła. Wyrzucenie reszki.
Losowanie jednej kuli z pudełka, w którym są kule białe, czerwone i żółte.	Wylosowanie białej kuli. Wylosowanie czerwonej kuli. Wylosowanie żółtej kuli.
Rzut czworościenną kostką do gry, na ściankach której zapisano liczby: $5$ , $5$ , $8$ , $9$ .	Wyrzucenie $5$ . Wyrzucenie $8$ . Wyrzucenie $9$ .

Zdarzenie losowe składa się ze zdarzeń elementarnych, które nazywamy zdarzeniami sprzyjającymi temu zdarzeniu.

Liczbę zdarzeń elementarnych, z których składa się dane zdarzenie losowe, nazywamy liczebnością (lub mocą) zdarzenia losowego.

Przykład 3

Rzucamy sześcienną kostką do gry.
Niech $A$ będzie zdarzeniem losowym polegającym na wyrzuceniu nieparzystej liczby oczek. Zdarzenia elementarne sprzyjające temu zdarzeniu losowemu to: wyrzucenie $1$ , wyrzucenie $3$ , wyrzucenie $5$ .

Rob4oId488QZ5

Na grafice ukazane są trzy sześcienne kostki do gry w kolorze białym. Na pierwszej wylosowano jedno oczko, na drugiej trzy, a na trzeciej pięć. — Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Możemy zapisać:

A = \{1, 3, 5\}

Zdarzeniu $A$ sprzyjają trzy zdarzenia elementarne. Liczebność (moc) zbioru $A$ jest równa $3$ .

Przykład 4

Rzucamy monetą i sześcienną kostką do gry.
Niech $A$ będzie zdarzeniem losowym polegającym na wyrzuceniu reszki i liczby oczek większej od dwóch.
Zdarzeniu $A$ sprzyjają zdarzenia elementarne:

wyrzucono reszkę i $3$ ,
wyrzucono reszkę i $4$ ,
wyrzucono reszkę i $5$ ,
wyrzucono reszkę i $6$ .

RdT7mnzEvuSjz

Na grafice ukazane są cztery sześcienne kostki do gry w kolorze białym oraz cztery monety pięciozłotowe odwrócone reszką. Ustawione są naprzemiennie. Na pierwszej kostce wylosowano trzy oczka, na drugiej cztery, na trzeciej pięć, a na czwartej sześć. — Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Zdarzenia sprzyjające w tym przypadku możemy opisać za pomocą uporządkowanych par, których pierwszym elementem jest reszka $R$ , a drugim liczba większa od dwóch.

A = \{(R, 3), (R, 4), (R, 5), (R, 6)\}

Zdarzeniu $A$ sprzyjają $4$ zdarzenia elementarne.

Przykład 5

Rzucamy dwiema monetami.
Niech $B$ będzie zdarzeniem losowym: wypadły dwa orły.
Zdarzeniu $B$ sprzyja tylko jedno zdarzenie elementarne: na pierwszej monecie wypadł orzeł i na drugiej monecie wypadł orzeł.

RKxMj90OMje4v

Na grafice znajduje się moneta pięciozłotowa i jednogroszowa. Obie monety odwrócone są orzełkiem. — Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Zapisujemy:

B = \{(O, O)\}

Zbiór zdarzeń elementarnych

Dla każdego doświadczenia losowego należy określić, co uważamy za zdarzenie elementarne i określić zbiór wszystkich możliwych zdarzeń elementarnych. Zbiór ten nazywamy zbiorem zdarzeń elementarnych lub przestrzenią zdarzeń elementarnych.

Zbiorem zdarzeń elementarnychZbiorem zdarzeń elementarnych nazywamy zbiór wszystkich możliwych wyników danego doświadczenia losowego.

Zbiór zdarzeń elementarnych oznaczamy zwykle literą $Ω$ (omega).

Przykład 6

Rzucamy czworościenną kostką do gry, na ściankach której zapisane są symbole: $+$ , $*$ , $%$ , $#$ .

$Ω = \{+, *, %, #\}$

Przykład 7

W tabelce zawarte są przykłady doświadczeń losowych i zbiorów zdarzeń elementarnych dla tych doświadczeń.

Doświadczenie losowe	Zbiór zdarzeń elementarnych
Rzut monetą.	$Ω = \{O, R\}$
Rzut sześcienną kostką do gry.	$Ω = \{1, 2, 3, 4, 5, 6\}$ .
Losowanie kuli z pudełka zawierającego dwie ponumerowane $(1, 2)$ kule białe i kulę zieloną.	$Ω = \{B 1, B 2, Z\}$
Rzut dwiema monetami..	$Ω = \{(O, O), (R, O), (O, R), (R, R)\}$ .

Przykład 8

Na stole leżą trzy karteczki. Na każdej karteczce zapisana jest jedna z cyfr: $1$ , $2$ , $3$ . Doświadczenie polega na wylosowaniu najpierw jednej karteczki, zatrzymaniu jej i wylosowaniu drugiej karteczki. Z cyfr zapisanych na karteczkach tworzymy liczby dwucyfrowe. Cyfra dziesiątek będzie cyfrą zapisaną na pierwszej karteczce, a cyfrą jedności – cyfra zapisana na drugiej karteczce.

R7490p79pZTB2

Na grafice znajdują się trzy kolorowe karteczki. Pierwsza jest różowa i znajduje się na niej cyfra jeden. Druga jest żółta i znajduje się na niej cyfra dwa. Trzecia jest niebieska i znajduje się na niej cyfra trzy. — Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Określimy zbiór zdarzeń elementarnych i zdarzeń losowych:
$P$ – utworzona liczba będzie parzysta,
$B$ – utworzona liczba będzie liczbą pierwszą,
$C$ – utworzona liczba będzie większa od $30$ .

Ω = \{12, 13, 21, 23, 31, 32\}

P = \{12, 32\}

B = \{13, 23, 31\}

C = \{31, 32\}

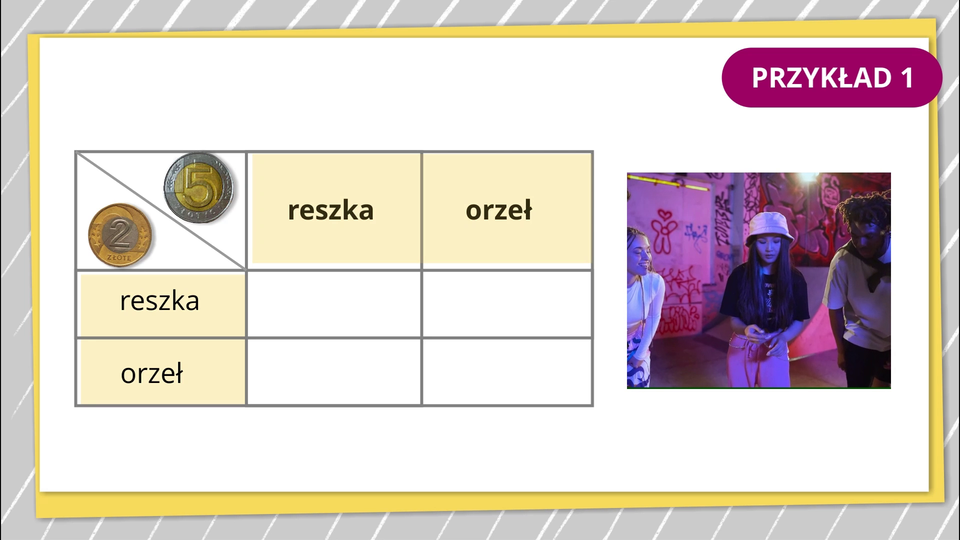
Prezentacja multimedialna

Polecenie 1

Przeanalizuj przykłady zamieszczone w prezentacji, pokazujące różne sposoby graficznego przedstawiania doświadczeń losowych.

R1bKMs55kFuEB

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Transkrypcjaazurewhite

RDYaLfdsjsEdr

RC1Vft6EQmQdl

Na grafice jest białe tło. Ramka jest w kolorze szaro‑żółtym w białe paski. W prawym górnym rogu znajduje się tekst. Przykład 1. Napis jest na fioletowym tle. W centralnej części ekranu znajduje się tekst. Rzucamy dwiema monetami. Poniżej ukazane są dwie dwuzłotówki. Jedna jest odwrócona reszką, pod nią znajduje się napis: r - reszka. Druga jest odwrócona orzełkiem, pod nią znajduje się napis: o - orzeł. Tuż obok znajdują się dwie pięciozłotówki. Jedna jest odwrócona reszką, pod nią znajduje się napis: R - reszka. Druga jest odwrócona orzełkiem, pod nią znajduje się napis: O - orzeł. — Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Transkrypcjaazurewhite

Przykład pierwszy
Rzucamy dwiema monetami - dwuzłotówką i pięciozłotówką. Niech $r$ oznacza otrzymanie reszki, a $o$ - orła na monecie dwuzłotowej.
Niech $R$ oznacza otrzymanie reszki, a $O$ - otrzymanie orła na monecie pięciozłotowej.

R1K2fv54oujlu

Transkrypcjaazurewhite

R1Kat3dozk8iU

R12WCLsRXlN5O

Na grafice jest białe tło. Ramka jest w kolorze szaro‑żółtym w białe paski. W prawym górnym rogu znajduje się tekst. Przykład 2. Napis jest na fioletowym tle. W centralnej części ekranu znajduje się tekst. Kod składa się z jednej spośród liter: E, F, G, H i następującej po niej jednej z cyfr: 4, 5, 6. Poniżej ukazany jest szary prostokąt z niebieskim obramowaniem, a na nim napisane jest E4. Napis w kolorze białym. W dolnej części ekranu jest tekst. Określimy, ile może być takich kodów. — Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Transkrypcjaazurewhite

R5OhmldfxJdKE

RniyMbPJETQBT

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Transkrypcjaazurewhite

R1AB5CWgJgni8

RZ97CCR0XhVNr

Transkrypcjaazurewhite

RPoUbeVKiAvuh

RVmpBQFLUAckp

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Transkrypcjaazurewhite

R17nBkSCVhDif

R1ZzUT5BHVtjv

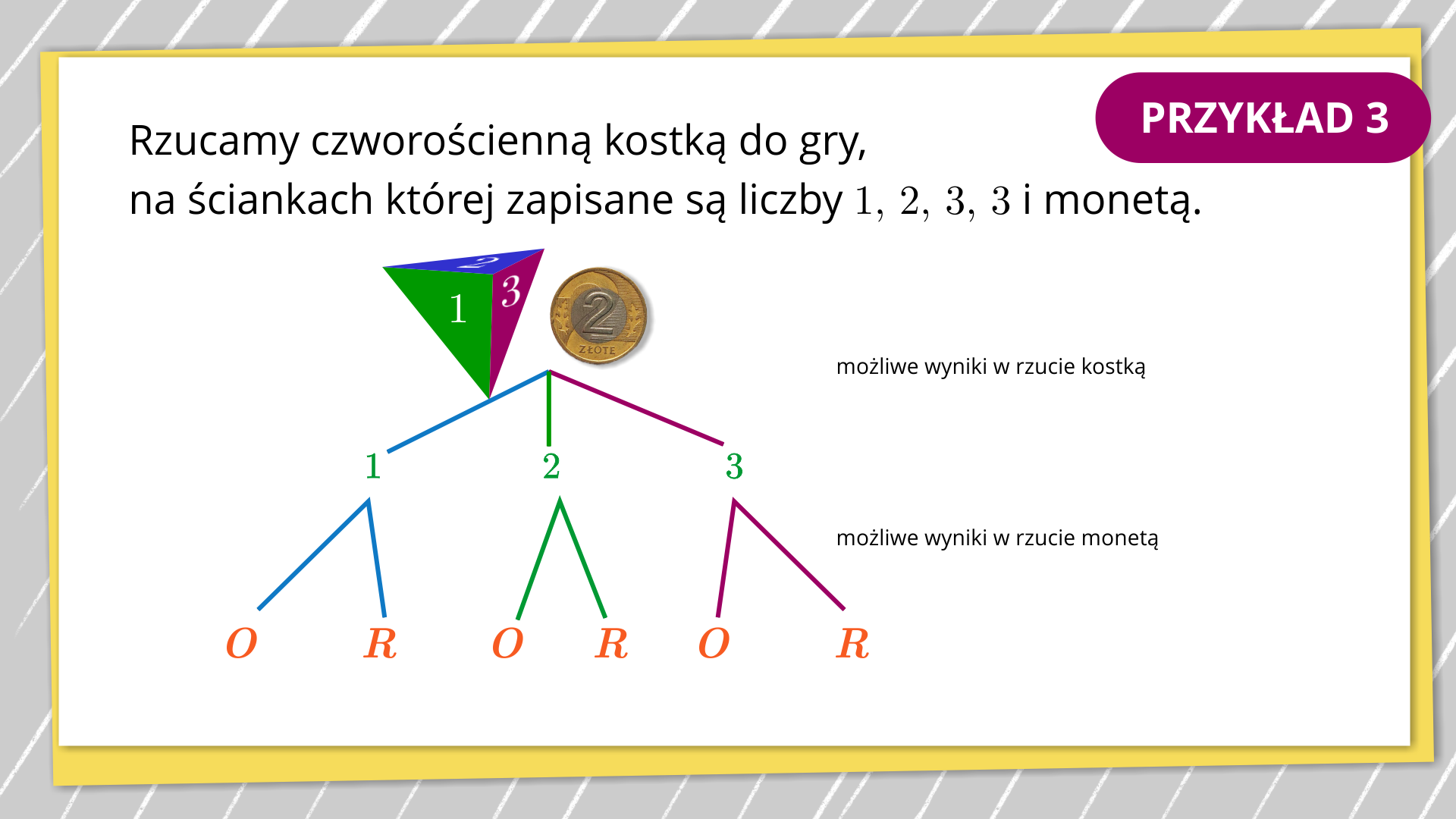
Ilustracja — Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Transkrypcjaazurewhite

RizPUtQEyZ4Y3

R1On0I9wzhQeW

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Transkrypcjaazurewhite

R1FdrM9XgYUvY

R19wmk81y59K3

Na animacji jest białe tło. Ramka jest w kolorze szaro‑żółtym w białe paski. W prawym górnym rogu znajduje się tekst. Przykład 4. Napis jest na fioletowym tle. Na slajdzie znajduje się napis: Ania ma bluzkę w kolorze niebieskim, bluzkę w kolorze pomarańczowym i bluzkę w kolorze zielonym. Poniżej ukazane są trzy bluzki w wymienionych kolorach. Pod grafikami znajduje się napis. Ma dwie spódnice: zieloną i pomarańczową. Poniżej znajdują się dwie spódnice w wymienionych kolorach. — Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Transkrypcjaazurewhite

R1CJ2jqdrMQFz

RPiiOWqHpoQHh

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Transkrypcjaazurewhite

Polecenie 2

Korzystając z grafu zamieszczonego w Przykładzie $4$ prezentacji, określ ile ma Ania możliwości zestawienia

spódnicy i bluzki w tym samym kolorze,
spódnicy pomarańczowej i bluzki,
spódnicy w innym kolorze niż bluzka.

R1Y9Odf9nVFiD

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Polecenie 3

Doświadczenie polega na dwukrotnym rzucie sześcienną kostką. Wzorując się na Przykładzie $2$ zamieszczonym w prezentacji, sporządź tabelkę wszystkich możliwych wyników tego doświadczenia.
Wypisz wyniki sprzyjające następującym zdarzeniom losowym:
$A$ – za pierwszym razem wypadła $4$ ,
$B$ – w obu rzutach wypadła ta sama liczba oczek,
$C$ – za drugim razem wypadła mniejsza liczba oczek niż za pierwszym i nie większa niż $3$ .

R100y7pH7lcnm

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Rysujemy tabelę – w pierwszej kolumnie umieszczamy liczbę oczek, które mogą wypaść w pierwszym rzucie, a w pierwszym wierszu – liczbę oczek, które mogą wypaść w drugim rzucie.

	$1$	$2$	$3$	$4$	$5$	$6$
$1$	$1$ , $1$	$1$ , $2$	$1$ , $3$	$1$ , $4$	$1$ , $5$	$1$ , $6$
$2$	$2$ , $1$	$2$ , $2$	$2$ , $3$	$2$ , $4$	$2$ , $5$	$2$ , $6$
$3$	$3$ , $1$	$3$ , $2$	$3$ , $3$	$3$ , $4$	$3$ , $5$	$3$ , $6$
$4$	$4$ , $1$	$4$ , $2$	$4$ , $3$	$4$ , $4$	$4$ , $5$	$4$ , $6$
$5$	$5$ , $1$	$5$ , $2$	$5$ , $3$	$5$ , $4$	$5$ , $5$	$5$ , $6$
$6$	$6$ , $1$	$6$ , $2$	$6$ , $3$	$6$ , $4$	$6$ , $5$	$6$ , $6$

a) $A = \{(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6)\}$
b) $B = \{(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)\}$
c) $C = \{(2, 1), (3, 1), (3, 2), (4, 1), (4, 2), (4, 3), (5, 1), (5, 2), (5, 3), (6, 1), (6, 2), (6, 3)\}$

Rs6itgDZmiLhz

Ćwiczenie 1

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

RBoGxX7xCLHny

Ćwiczenie 2

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

RySWECANryIiP

Ćwiczenie 3

Rzucamy sześcienną kostką do gry. Połącz zdarzenie losowe ze zdarzeniami mu sprzyjającymi. Wyrzucenie parzystej liczby oczek. Możliwe odpowiedzi: 1.

2

4

6

, 2.

3

6

, 3.

4

, 4.

1

6

, 5.

3

4

5

6

Wyrzucenie liczby oczek równej

1

lub

6

. Możliwe odpowiedzi: 1.

2

4

6

, 2.

3

6

, 3.

4

, 4.

1

6

, 5.

3

4

5

6

Wyrzucenie liczby oczek równej co najmniej trzy. Możliwe odpowiedzi: 1.

2

4

6

, 2.

3

6

, 3.

4

, 4.

1

6

, 5.

3

4

5

6

Wyrzucenie liczby oczek równej

4

. Możliwe odpowiedzi: 1.

2

4

6

, 2.

3

6

, 3.

4

, 4.

1

6

, 5.

3

4

5

6

Wyrzucenie liczby oczek podzielnej przez trzy. Możliwe odpowiedzi: 1.

2

4

6

, 2.

3

6

, 3.

4

, 4.

1

6

, 5.

3

4

5

6

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

R1ZM3fYetHNZ1

Ćwiczenie 4

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Ćwiczenie 5

Na rysunku przedstawiono siatkę nietypowej kostki do gry.

RBnFTXU1TbeDp

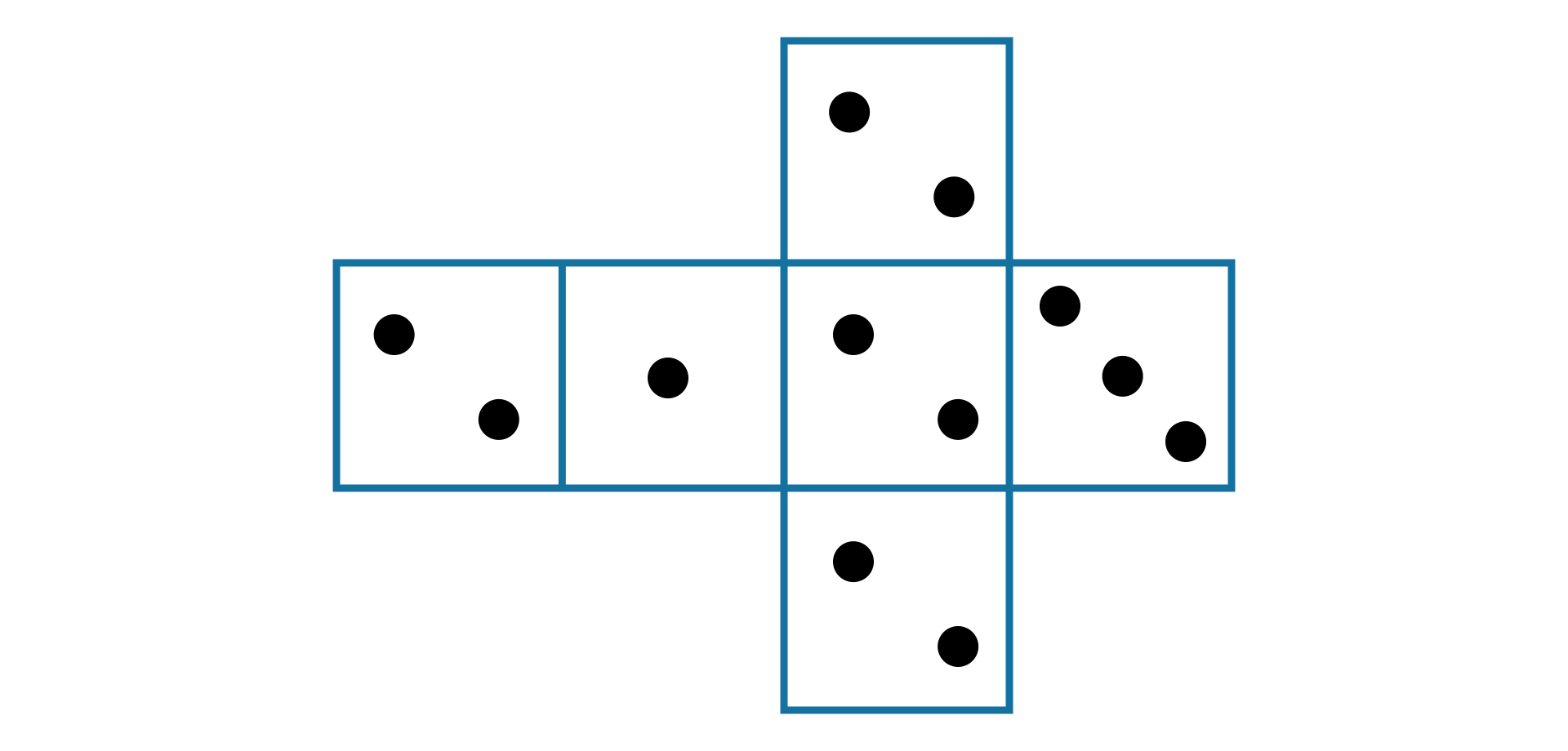
Na grafice ukazana jest siatka nietypowej kostki do gry. Na jednej ściance jest jedno oczko, na drugiej są trzy, natomiast na czterech pozostałych ściankach są po dwa oczka. — Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

RgK5fN1ZHGLvp

Łączenie par. Oceń prawdziwość podanych zdań. Zaznacz PRAWDA, gdy zdanie jest prawdziwe, albo FAŁSZ, gdy zdanie jest fałszywe.. W doświadczeniu polegającym na rzucie kostką liczba zdarzeń elementarnych jest równa

6

.. Możliwe odpowiedzi: Prawda, Fałsz. W doświadczeniu polegającym na dwukrotnym rzucie kostką liczba zdarzeń elementarnych jest równa

9

.. Możliwe odpowiedzi: Prawda, Fałsz. Rzucamy kostką. Liczba zdarzeń sprzyjających wyrzuceniu liczby oczek równej

5

jest równa

1

.. Możliwe odpowiedzi: Prawda, Fałsz. Rzucamy dwa razy kostką. Liczba zdarzeń sprzyjających zdarzeniu polegającemu na wylosowaniu dwóch liczb oczek, których suma jest równa

6

3 .

. Możliwe odpowiedzi: Prawda, Fałsz

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Ćwiczenie 6

RiYiNhb4BcTAy

Doświadczenie polega na wyciągnięciu jednej karty z talii

52

kart.
Uzupełnij zdania, przeciągając odpowiednie liczby.
Aby mieć pewność, że na pewno wyciągniemy kartę koloru pik, trzeba wyciągnąć co najmniej 1.

21

, 2.

27

, 3.

21

, 4.

14

, 5.

40

, 6.

18

kart.
Aby mieć pewność, że na pewno wyciągniemy kartę koloru pik lub karo, trzeba wyciągnąć co najmniej 1.

21

, 2.

27

, 3.

21

, 4.

14

, 5.

40

, 6.

18

kart.
Aby mieć pewność, że na pewno wyciągniemy kartę koloru pik, karo lub trefl, trzeba wyciągnąć co najmniej 1.

21

, 2.

27

, 3.

21

, 4.

14

, 5.

40

, 6.

18

kart.

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Pokaż przykładowy opis rozumowaniaazurewhite

Zauważmy, że wyciągając $39$ kart z talii, możliwe jest wyciągnięcie $13$ kart koloru trefl, $13$ kart koloru karo i $13$ kart koloru kier. Wówczas w talii pozostanie $13$ kart koloru pik. Zatem, aby mieć pewność, że wyciągniemy kartę koloru pik, musimy wyciągnąć co najmniej $40$ kart z talii.
Zauważmy, że wyciągając $26$ kart z talii, możliwe jest wyciągnięcie $13$ kart koloru trefl i $13$ kart koloru kier. Wówczas w talii pozostanie $13$ kart koloru pik i $13$ kart koloru karo. Zatem, aby mieć pewność, że wyciągniemy kartę koloru pik lub karo, musimy wyciągnąć co najmniej $27$ kart z talii.
Zauważmy, że wyciągając $13$ kart z talii, możliwe jest wyciągnięcie $13$ kart koloru kier. Wówczas w talii pozostanie $13$ kart koloru pik, $13$ kart koloru trefl i $13$ kart koloru karo. Zatem, aby mieć pewność, że wyciągniemy kartę koloru pik, karo lub trefl, musimy wyciągnąć co najmniej $14$ kart z talii.

Ćwiczenie 7

Doświadczenie losowe polega na wylosowaniu jednej liczby spośród wszystkich liczb dwucyfrowych. Wypisz wyniki sprzyjające zdarzeniom:
$A$ – wylosowana liczba będzie podzielna przez $10$ ,
$B$ – wylosowana liczba będzie liczbą pierwszą, mniejszą od $20$ ,
$C$ – wylosowana liczba będzie kwadratem liczby jednocyfrowej,
$D$ – wylosowana liczba będzie dzielnikiem liczby $100$ .

R1SoL0BHMlP2K

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Jest $9$ liczb dwucyfrowych podzielnych przez $10$ .
Są $4$ liczby dwucyfrowe pierwsze, mniejsze od $20$ .
Jest $6$ liczb dwucyfrowych, które są kwadratami liczb jednocyfrowych.
Są $4$ liczby dwucyfrowe, będące dzielnikami liczby $100$ .

$A = \{10, 20, 30, 40, 50, 60, 70, 80, 90\}$
$B = \{11, 13, 17, 19\}$
$C = \{16, 25, 36, 49, 64, 81\}$
$D = \{10, 20, 25, 50\}$

Ćwiczenie 8

W szufladzie leżą kule takie, jak na rysunku.

R8oxBxCD4rH1s

Na grafice znajduje się kilka kolorowych kółek. Trzy są w kolorze zielonym, dwa są w kolorze niebieskim i dwa są w kolorze pomarańczowym. — Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

R9bnz0QuKF2DX

Na grafice znajduje się kilka kolorowych kółek. Trzy są w kolorze zielonym, dwa są w kolorze niebieskim i dwa są w kolorze czerwonym. — Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Wyciągamy z szuflady na chybił trafił najpierw jedną, a następnie drugą kulę. Przyjmujemy, że wynikiem doświadczenia jest para, której pierwszym elementem jest kolor ( $z$ – zielony, $n$ – niebieski, $c z$ – czerwony) pierwszej kuli, a drugim elementem kolor drugiej wyciągniętej kuli.
Podaj przykład doświadczenia losowego, które opisano następująco:

A = \{(z, z), (z, n), (z, c z)\}

B = \{(c z, c z), (n, n), (z, z)\}

C = \{(n, n), (n, c z), (c z, n), (c z, c z)\}

R1bbcARvgDjTy

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

$(z, z)$ – wylosowano dwie kule zielone
$(n, z)$ – pierwsza z wylosowanych kul to kula niebieska, a druga to kula zielona
$(c z, n)$ – wylosowano kulę czerwoną i kulę niebieską

$A$ – w losowaniu dwóch kul z szuflady pierwszą kulą będzie kula zielona.
$B$ – w losowaniu dwóch kul z szuflady obie kule będą tego samego koloru.
$C$ – w losowaniu dwóch kul z szuflady, żadna z kul nie będzie zielona.

Słownik

Doświadczenie losowe

Eksperyment, który może być powtarzany w warunkach identycznych (lub zbliżonych), wyniku którego nie da się jednoznacznie przewidzieć.

Zbiór (przestrzeń) zdarzeń elementarnych

Zbiór wszystkich możliwych wyników danego doświadczenia losowego.

Zdarzenie elementarne

Zdarzenie elementarne to pojedynczy wynik doświadczenia losowego.

Zdarzenie losowe

Każdy zbiór zdarzeń elementarnych spełniających określony warunek nazywamy zdarzeniem losowym.

Notatnik

Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.

R1b8OvSPUG8s3

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

2. Obliczanie prawdopodobieństwa w prostych sytuacjach losowych

Rachunek prawdopodobieństwa