Powtórzenie - statystyka, kombinatoryka, prawdopodobieństwo
1. Powtórzenie
Statystyka
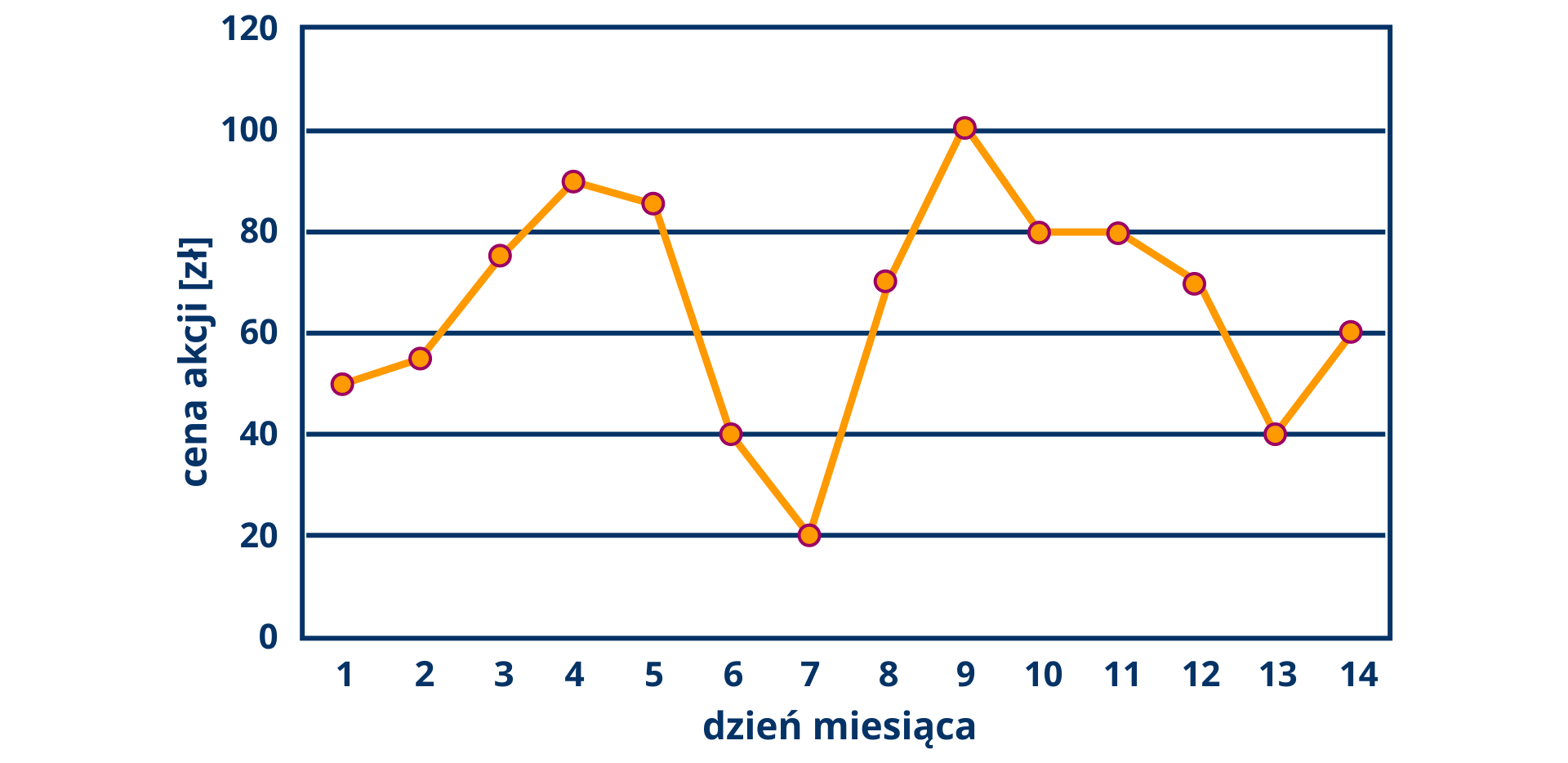
Wykres przedstawia zmiany cen akcji pewnej firmy w ciągu kolejnych czternastu dni lipca pewnego roku.
W tabeli przedstawiono dane dotyczące liczby lokatorów i mieszkań w pewnym bloku.
Liczba mieszkań | Liczba lokatorów | W tym dzieci |
|---|---|---|
Uzupełnij lukę w zdaniu, wpisując odpowiednią liczbę. Wszystkich mieszkań jest Tu uzupełnij.
Uzupełnij poniższą lukę. Kliknij w nią, aby rozwinąć listę, a następnie wybierz poprawną odpowiedź. Takich mieszkań jest 1. , 2. , 3. , 4. , 5. , 6. .
Uzupełnij lukę w zdaniu, wpisując odpowiednią liczbę. W tym bloku mieszka Tu uzupełnij dorosłych osób.
Uzupełnij poniższą lukę. Kliknij w nią, aby rozwinąć listę, a następnie wybierz poprawną odpowiedź. Mieszkań również zamieszkiwanych przez dzieci jest 1. , 2. , 3. , 4. , 5. , 6. .
Uzupełnij lukę w zdaniu, wpisując odpowiednią liczbę. W tym bloku mieszka Tu uzupełnij dzieci.
Poniższy diagram kołowy przedstawia procentowy podział powierzchni lądów i oceanów na Ziemi.
Źródło: Świat w liczbach .

Poniższe diagramy słupkowe przedstawiają dane dotyczące powierzchni poszczególnych kontynentów i oceanów.
Źródło: Świat w liczbach .
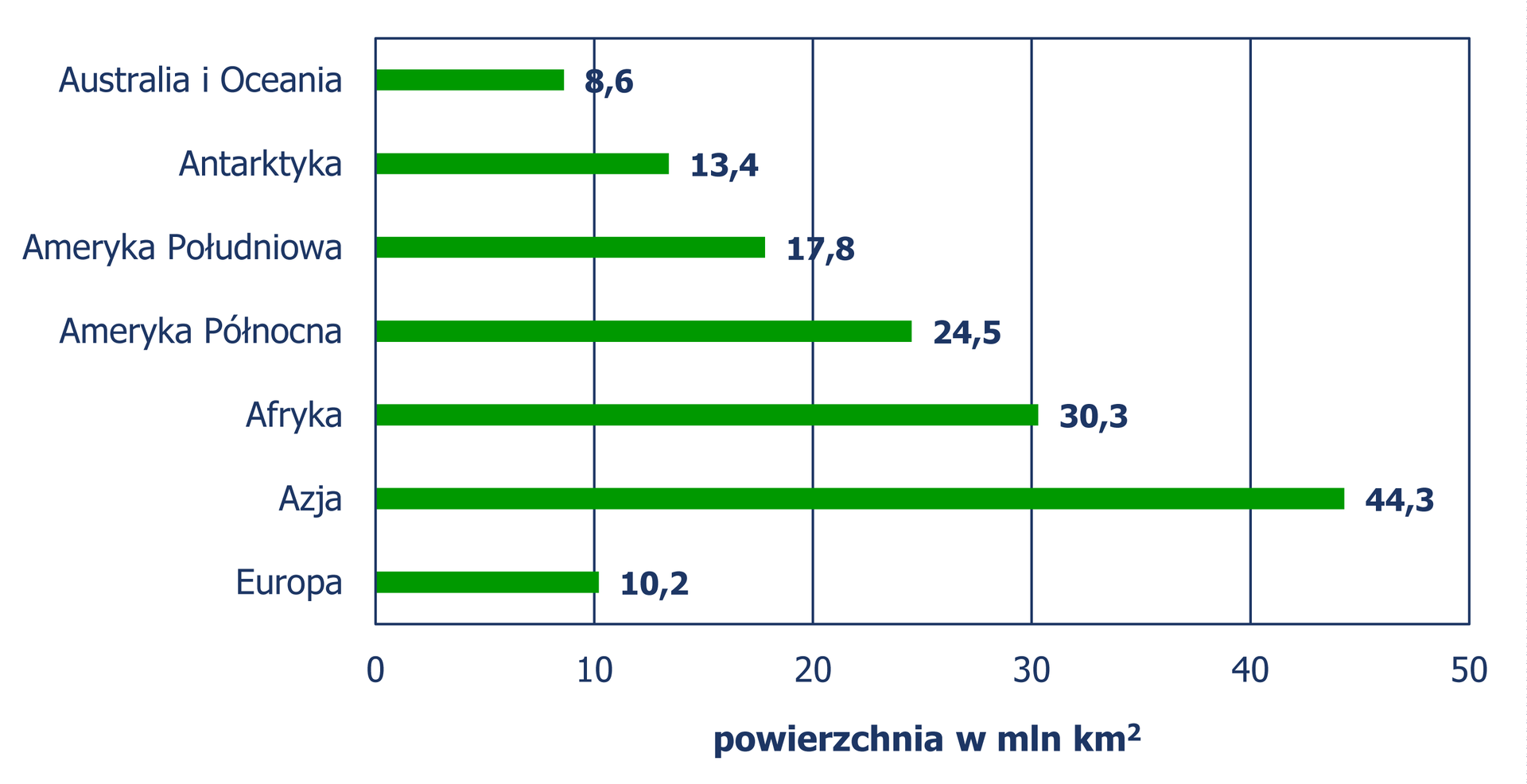

Uzupełnij poniższe luki. Kliknij w nie, aby rozwinąć listę, a następnie wybierz poprawną odpowiedź. Afryka zajmuje 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. powierzchni lądów Ziemi, a Europa zajmuje 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. .
Uzupełnij lukę w zdaniu, wpisując odpowiednią liczbę. Powierzchnia Azji jest większa niż powierzchnia Antarktyki o Tu uzupełnij .
Uzupełnij lukę w zdaniu, wpisując odpowiednią liczbę. Powierzchnia Oceanu Arktycznego stanowi Tu uzupełnij powierzchni oceanów Ziemi.
Uzupełnij lukę w zdaniu, wpisując odpowiednią liczbę. Powierzchnia Oceanu Atlantyckiego jest mninejsza o Tu uzupełnij od powierzchni Oceanu Spokojnego.
Na diagramie słupkowym przedstawiono liczbę imprez oświatowych w muzeach w roku.
Źródło: GUS
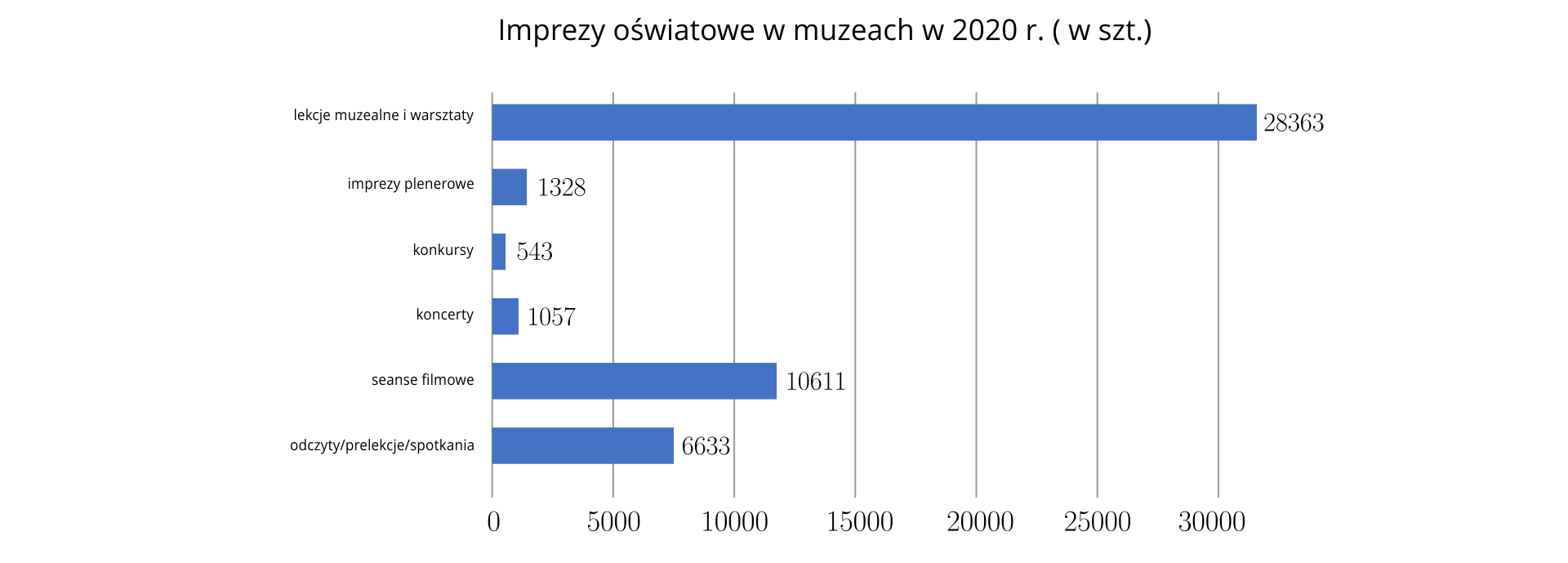
Przedstaw te dane na diagramie kołowym.
Opisz jak będą wyglądały te dane na diagramie kołowym.
Kombinatoryka i prawdopodobieństwo
Prawdopodobieństwem zdarzenia losowego () nazywamy stosunek liczby wyników sprzyjających temu zdarzeniu () do liczby wszystkich możliwych wyników () tego zdarzenia losowego.
W tym materiale omówimy sposoby obliczania prawdopodobieństwa zdarzeń podczas dwukrotnego rzutu kostką lub monetą oraz w innych sytuacjach z życia codziennego, a także zasady stosowania reguły mnożenia oraz reguły dodawania, również w sytuacjach wymagających rozważenia kilku przypadków.
Film dostępny pod adresem /preview/resource/Rg0IeMgONyCQl
Animacja dotyczy rzutu dwoma identycznymi monetami, na ekranie po lewej stronie wyświetla się wykres a po prawej okienko z animacją rzutu monetami.
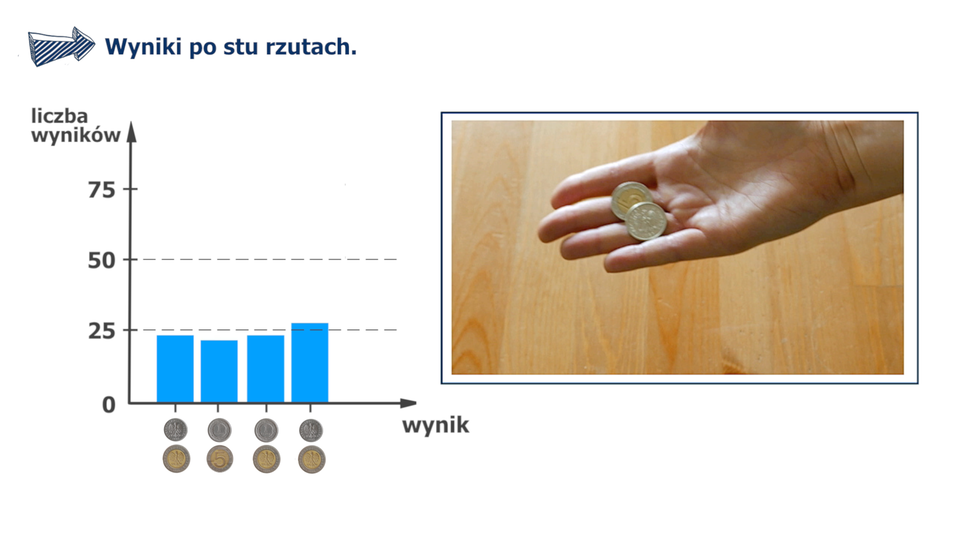
Film dostępny pod adresem /preview/resource/RCt0lAtOOCTVi
Animacja dotyczy rzutu dwoma różnymi monetami, na ekranie po lewej stronie wyświetla się wykres a po prawej okienko z animacją rzutu monetami.
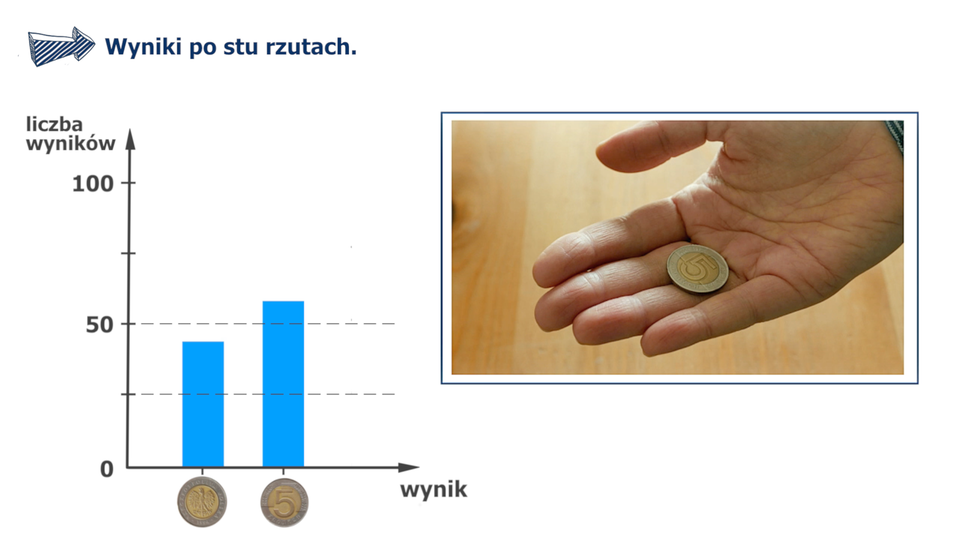
Film dostępny pod adresem /preview/resource/RXHxczROhHyrh
Animacja dotyczy rzutu jedną monetą, na ekranie po lewej stronie wyświetla się wykres a po prawej okienko z animacją rzutu monetami.
Wykonaj rzutów monetą. Porównaj swoje wyniki z wynikami przedstawionymi w Przykładzie .
Czy stwierdzenia sformułowane w filmie są prawdziwe dla Twoich wyników?
Film dostępny pod adresem /preview/resource/R8jXF43Qe6AON
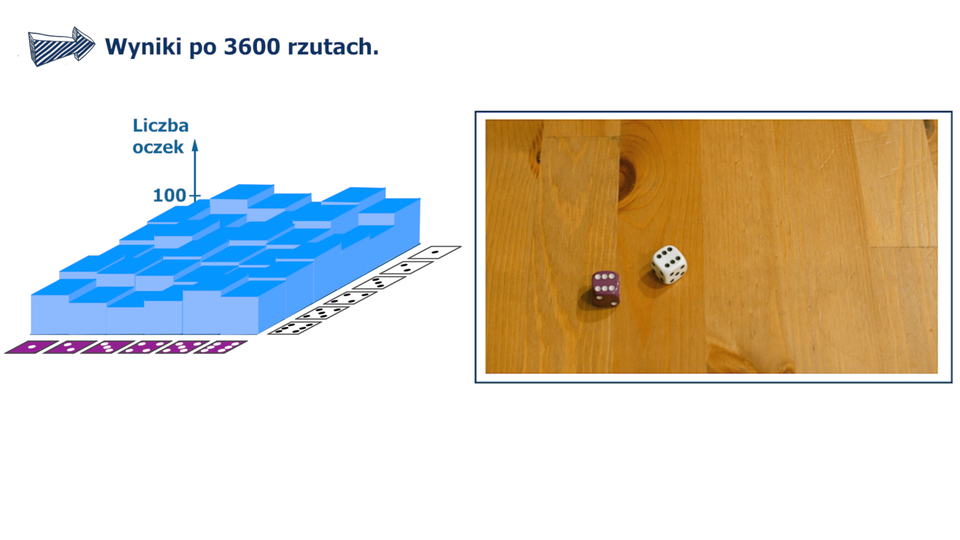
Animacja dotyczy rzutu dwoma kostkami, na ekranie po lewej stronie wyświetla się wykres a po prawej okienko z animacją rzutu kostkami.
Film dostępny pod adresem /preview/resource/RcuTrTcBwwe2H
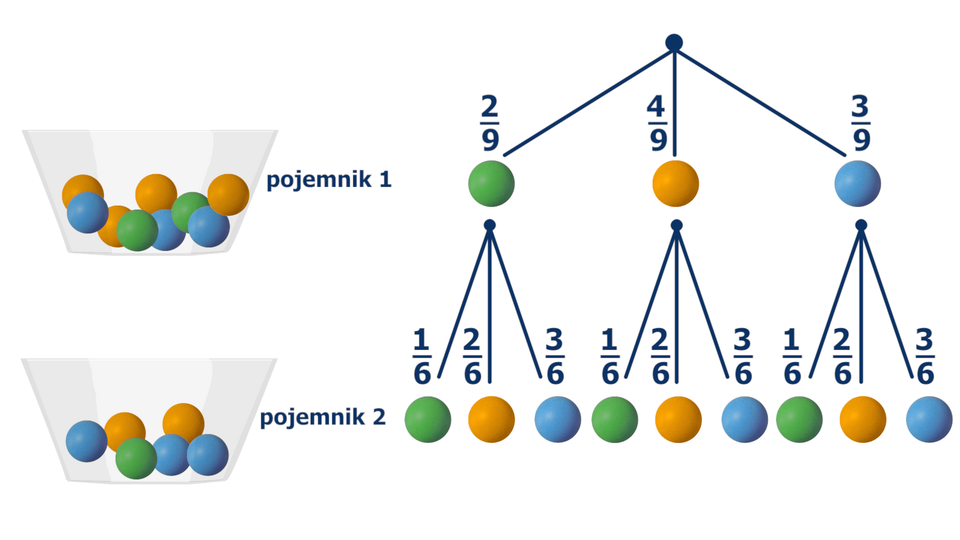
Animacja dotyczy losowania kul z dwóch pojemników. W pojemnikach znajdują się kule różnego koloru. Po prawej stronie wyświetla się drzewko przedstawiające prawdopodobieństwa wylosowania danego koloru kuli.

Film dostępny pod adresem /preview/resource/RjCkmcufP0rag
Animacja przedstawia dwie kobiety w sklepie, kobiety chcą kupić bluzki, niekoniecznie w tych samych kolorach, po prawej stronie wyświetlają się kombinacje kolorów bluzek, które kobiety mogą zakupić.

Film dostępny pod adresem /preview/resource/R6JfSCvbrlOct
Animacja przedstawia dwie kobiety w sklepie, kobiety chcą kupić bluzki, w różnych kolorach, po prawej stronie wyświetlają się kombinacje kolorów bluzek, które kobiety mogą zakupić.

Film dostępny pod adresem /preview/resource/R1FsEGWtJqY49
Animacja przedstawia dwie kobiety w sklepie, kobiety chcą kupić dwie bluzki, po prawej stronie wyświetlają się kombinacje kolorów bluzek, które kobiety mogą zakupić.

Film dostępny pod adresem /preview/resource/RY6mVoEjzcqLU
Animacja przedstawia dwie kobiety w sklepie, kobiety chcą kupić dwie bluzki, w różnych kolorach, po prawej stronie wyświetlają się kombinacje kolorów bluzek, które kobiety mogą zakupić.

Film dostępny pod adresem /preview/resource/RfZYbeEJL5Fqu
Animacja przedstawia sposoby na zajęcia miejsc przy dwuosobowych, trzyosobowych oraz czteroosobowych stolikach. Po prawej stronie wyświetlają się sposoby umiejscowienia osób.
Reguła mnożenia
Liczba par elementów, w których pierwszy element pary można wybrać na sposobów, a drugi element pary na sposobów jest równa .
Regułę mnożenia można uogólnić dla trzech, czterech elementów.
Kuba postanowił zjeść obiad w stołówce szkolnej. Na ile sposobów Kuba może wybrać posiłek, jeżeli dziś ma ochotę na zupę, drugie danie i deser?
Z reguły mnożenia wynika,że Kuba może wybrać posiłek na sposoby.
Reguła dodawania
Jeżeli mamy dwa zbiory, jeden składający się z elementów, drugi składający się z elementów i żaden element nie powtarza się w obu zbiorach, to wybierając element z tych zbiorów, możemy to zrobić na sposobów.
Regułę dodawania można uogólnić na trzy, cztery zbiory.
Regułę dodawania stosujemy przy wyborze typu albo‑albo.
Kuba postanowił zjeść obiad w stołówce szkolnej. Na ile sposobów Kuba może wybrać posiłek, jeżeli dziś ma ochotę na zupę i drugie danie, albo drugie danie i deser?
możliwości
Z reguły mnożenia i reguły dodawania wynika, że Kuba może wybrać posiłek na sposobów.
Rzucamy jednokrotnie sześcienną kostką do gry. Połącz w pary nazwy zdarzeń z ich prawdopodobieństwami.
<math><mfrac><mn>2</mn><mn>3</mn></mfrac></math>, <math><mfrac><mn>1</mn><mn>6</mn></mfrac></math>, <math><mfrac><mn>1</mn><mn>2</mn></mfrac></math>, <math><mn>1</mn></math>, <math><mfrac><mn>1</mn><mn>3</mn></mfrac></math>
| A:Wyrzucimy nie mniej niż trzy oczka | |
| B:Wyrzucimy liczbę oczek podzielną przez trzy | |
| C:Wyrzucimy liczbę oczek będącą liczbą pierwszą | |
| D:Wyrzucimy liczbę oczek nie większą niż sześć | |
| E:Wyrzucimy liczbę oczek nie większą niż 1 |
- Prawdopodobieństwo zdarzenia, że suma oczek na obu kostkach będzie liczbą większą od , wynosi .
- Prawdopodobieństwo zdarzenia, że iloczyn oczek na obu kostkach będzie liczbą podzielną przez , wynosi .
- Prawdopodobieństwo zdarzenia, że liczba oczek na pierwszej kostce jest większa niż na drugiej kostce, wynosi .
- Prawdopodobieństwo zdarzenia, że liczba oczek na pierwszej kostce będzie parzysta, a liczba oczek na drugiej kostce będzie podzielna przez trzy, wynosi .
- 1
Kamila: "Prawdopodobieństwo, że podczas losowania z urny dwóch kul wylosujemy kulę białą lub niebieską, wynosi ".
Bartek: "Prawdopodobieństwo, że za drugim razem wylosujemy kulę białą jest mniejsze lub równe prawdopodobieństwu, że wylosujemy kulę czarną".
Kinga: "Prawdopodobieństwo, że za drugim razem wylosujemy kulę czarną, jeżeli za pierwszym razem wylosowaliśmy kulę zieloną, wynosi ".
Maciek: "Prawdopodobieństwo, że wylosujemy kulę czarną jest większe od tego, że wylosujemy kulę zieloną lub niebieską".
Które z dzieci ma rację? Możliwe odpowiedzi: 1. Kamila, 2. Bartek, 3. Kinga, 4. Maciek
- Kamila
- Bartek
- Kinga
- Maciek
Rzucamy trzy razy monetą. Przeciągnij zdarzenia z dolnej sekcji do górnej, określając ich prawdopodobieństwa.
<math><msub><mi>A</mi><mo>1</mo></msub><mo>-</mo></math> wyrzucono co najmniej dwa orły., <math><msub><mi>A</mi><mo>3</mo></msub><mo>-</mo></math> wyrzucono co najmniej jedną reszkę., <math><msub><mi>A</mi><mo>6</mo></msub><mo>-</mo></math> wyrzucono dwie reszki i jednego orła., <math><msub><mi>A</mi><mo>5</mo></msub><mo>-</mo></math> wyrzucono nie więcej niż dwie reszki., <math><msub><mi>A</mi><mo>4</mo></msub><mo>-</mo></math> wyrzucono same orły lub same reszki., <math><msub><mi>A</mi><mo>2</mo></msub><mo>-</mo></math> wyrzucono dokładnie jedną reszkę.
W loterii jest losów, w tym wygrywających. Wyznacz prawdopodobieństwo zdarzenia, że druga osoba wylosuje los wygrywający, jeżeli:
osoba przed nią kupiła los przegrywający,
osoba przed nią kupiła los wygrywający,
Które z tych zdarzeń jest bardziej prawdopodobne?
Rozstrzygnij, czy zdanie jest prawdziwe, czy fałszywe.. Prawdopodobieństwo, że ulubionym kolorem losowo wybranej osoby spośród ankietowanych jest kolor niebieski, wynosi .. Możliwe odpowiedzi: Prawda, Fałsz. Prawdopodobieństwo, że ulubionym kolorem losowo wybranej osoby jest niebieski lub zielony, jest większe niż to, że ulubionym kolorem jest czerwony lub żółty.. Możliwe odpowiedzi: Prawda, Fałsz. Prawdopodobieństwo, że ulubionym kolorem dowolnie wybranej osoby jest żółty, jest dwukrotnie mniejsze od tego, że tym kolorem jest niebieski.. Możliwe odpowiedzi: Prawda, Fałsz. Prawdopodobieństwo, że ulubionym kolorem losowo wybranej osoby jest zielony, wynosi .. Możliwe odpowiedzi: Prawda, Fałsz
Ile wynosi prawdopodobieństwo, że losowo wybrana osoba otrzyma bilet z miejscem na parterze? Zaznacz prawidłową odpowiedź. Możliwe odpowiedzi: 1. , 2. , 3. , 4.
Kliknij w lukę, aby rozwinąć listę, i wybierz prawidłową odpowiedź. Odpowiedź: Prawdopodobieństwo to wynosi 1. , 2. , 3. , 4. .
Odp.1. , 2. , 3. , 4. , 5. , 6. , 7. , 8.
Niech będzie zbiorem wszystkich dodatnich liczb parzystych mniejszych od , - zbiorem wszystkich liczb pierwszych mniejszych od . Ile jest par , takich że i ?
Odp.1. , 2. , 3. , 4. , 5. , 6. , 7. , 8.
Niech będzie zbiorem dzielników liczby , - zbiorem wszystkich dodatnich liczb nieparzystych mniejszych od . Ile jest par , takich że i ?
Odp.1. , 2. , 3. , 4. , 5. , 6. , 7. , 8.
Ile jest kodów trzycyfrowych, gdzie żadna liczba nie może się powtarzać?
Odp. 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8.
Na zakończenie rozwiąż test podsumowujący, który sprawdza wiedzę z tego materiału.
Rachunek prawdopodobieństwa z kombinatoryką
Notatnik
Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.