Obliczenia pisemne na liczbach naturalnych
6. Porównywanie liczb naturalnych z zastosowaniem ilorazu
W wielu sytuacjach z życia codziennego zadajemy pytania: „o ile więcej”, „o ile mniej”, „ile razy więcej”, „ile razy mniej”. Pierwsze dwa z tych pytań służą do porównywania liczb za pomocą odejmowania. Jest to tzw. porównywanie różnicowe. Ostatnie dwa pytania stosujemy do porównywania liczb za pomocą mnożenia lub dzielenia. Taki rodzaj porównywania liczb nazywamy porównywaniem ilorazowym.
Dzielenie jest oprócz dodawania, odejmowania i mnożenia jednym z czterech podstawowych działań arytmetycznych. Dzielna jest to liczba, którą dzielimy przez drugą liczbę. Dzielnik jest to liczba przez którą dzielimy pierwszą liczbę, przy czym dzielnik jest zawsze różny od zera. IlorazIloraz to wynik dzielenia.
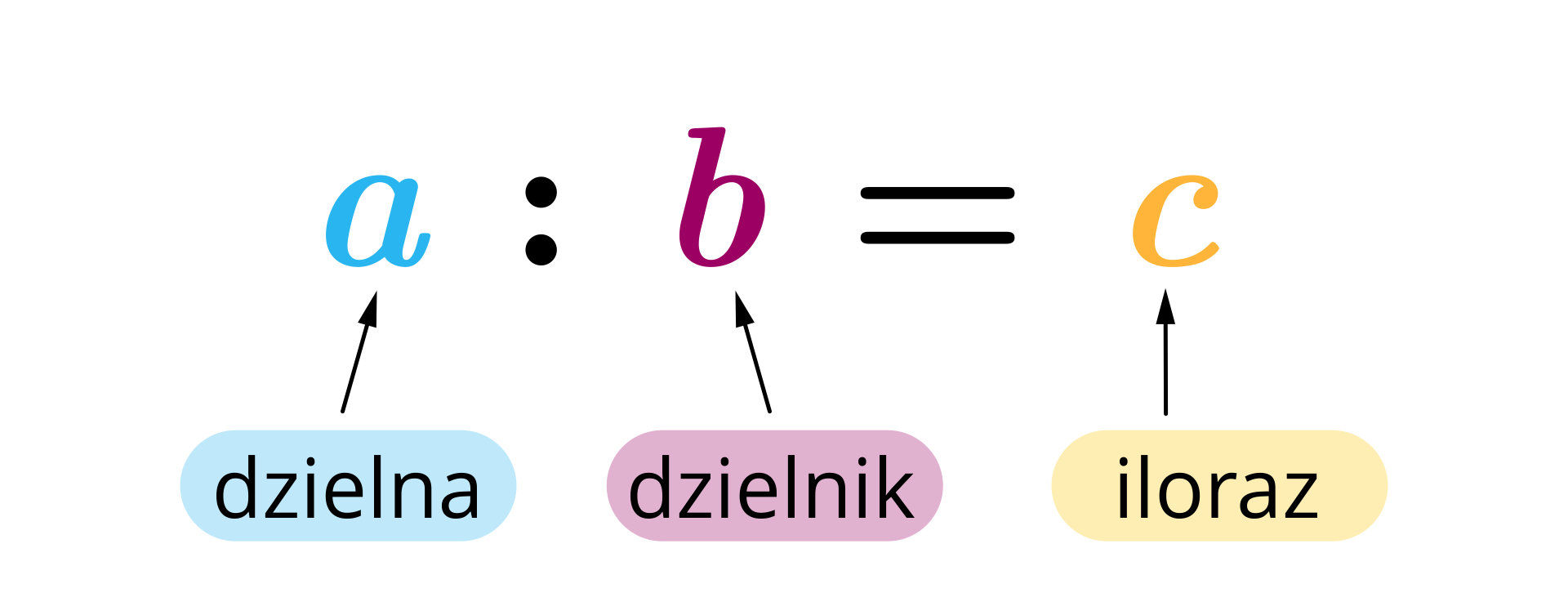
Załóżmy, że dane są liczby naturalne , , takie, że oraz jest liczbą większą od .
Jeżeli:
, to mówimy, że liczba jest razy większa od liczby ,
Oznacza to, że jeśli iloraz dwóch liczb jest większy od , to dzielna jest większa od dzielnika.
oraz , to .
Oznacza to, że jeśli iloraz dwóch liczb jest mniejszy od , to dzielnik jest większy od dzielnej.
Badanie zależności między dwiema liczbami za pomocą mnożenia lub dzielenia nazywamy porównywaniem ilorazowym tych liczb.
W celu sprawdzenia zależności pomiędzy liczbami naturalnymi przy użyciu porównywania ilorazowego, będziemy używać takich pytań jak: „ile razy więcej” oraz „ile razy mniej”.
Paweł ma w swojej skarbonce monet, a jego przyjaciel Tomek ma ich w swojej skarbonce razy więcej. Ile monet w swojej skarbonce ma Tomek?
Chcąc odpowiedzieć na to pytanie musimy wykonać następujące działanie.
Oznacza to, że Tomek ma w swojej skarbonce monet.
Na pierwszej półce z książkami leży książek, a na drugiej półce leży razy mniej książek. Ile książek leży na drugiej półce?
Chcąc odpowiedzieć na to pytanie musimy wykonać następujące działanie.
Oznacza to, że na drugiej półce znajduje się książek.
Marek i Jarek zbierali grzyby. Marek zebrał grzybów, a Jarek grzybów. Obliczymy, ile razy mniej zebrał grzybów Jarek niż Marek.
Rozwiązanie:
Do wyznaczenia zależności pomiędzy liczbą grzybów zebranych przez Marka, a liczbą grzybów zebranych przez Jarka, wystarczy wykonać następujące dzielenie:
Zauważmy, że .
Odpowiedź: Jarek zebrał razy mniej grzybów niż Marek.
Na parkingu jest samochodów osobowych, dostawczych oraz ciężarówki. Wyznaczymy:
ile razy mniej jest samochodów dostawczych niż osobowych,
ile razy więcej jest samochodów osobowych niż ciężarówek,
ile razy więcej jest samochodów dostawczych niż ciężarówek.
Rozwiązanie:
Wykonujemy dzielenie:
, zatem liczba jest razy mniejsza od liczby
Odpowiedź: Samochodów dostawczych jest razy mniej niż samochodów osobowych.
Wykonujemy dzielenie:
, zatem liczba jest razy większa od liczby
Odpowiedź: Samochodów osobowych jest razy więcej niż ciężarówek.
, zatem liczba jest razy większa od liczby
Odpowiedź: Samochodów dostawczych jest razy więcej niż ciężarówek.
W restauracji jest większych stolików, a przy każdym stoliku jest krzeseł oraz mniejszych stolików, a przy każdym stoliku są krzesła. Obliczymy, ile razy więcej jest krzeseł niż stolików w tej restauracji.
Rozwiązanie:
Wyznaczamy liczbę wszystkich krzeseł w restauracji:
Wyznaczamy liczbę wszystkich stolików w restauracji:
Obliczamy, ile razy więcej jest krzeseł niż stolików w tej restauracji:
Odpowiedź: W restauracji jest razy więcej krzeseł niż stolików.
Mateusz zebrał w skarbonce banknoty , banknoty po , jedną monetę , jedną monetę oraz jedną monetę . Łukasz ma w swojej skarbonce monety , monety oraz jedną monetę . Obliczymy, ile razy mniej pieniędzy zebrał Łukasz niż Mateusz.
Rozwiązanie:
Obliczamy kwotę pieniędzy zebranych przez Mateusza:
Obliczamy kwotę pieniędzy zebranych przez Łukasza:
Obliczamy, ile razy mniej pieniędzy zebrał Łukasz niż Mateusz:
Odpowiedź: Łukasz zebrał razy mniej pieniędzy niż Mateusz.
Klasa zebrała makulatury, klasa zebrała o makulatury mniej, a klasa o makulatury więcej niż klasa . Obliczymy:
ile razy mniej kilogramów makulatury zebrała klasa niż klasa ,
ile razy więcej kilogramów makulatury zebrała klasa niż klasa
Rozwiązanie:
Wyznaczmy liczbę kilogramów zebranej makulatury w poszczególnych klasach:
Klasa :
Klasa :
Klasa :
Obliczamy ile razy mniej kilogramów makulatury zebrała klasa niż klasa :
Odpowiedź: Klasa zebrała razy mniej kilogramów makulatury niż klasa .
Obliczamy ile razy więcej kilogramów makulatury zebrała klasa niż klasa
Odpowiedź: Klasa zebrała razy więcej kilogramów makulatury niż klasa .
Dane są liczby naturalne dodatnie , , , . Wykażemy, że jeśli liczba jest razy większa od liczby oraz liczba jest razy większa od liczby , to .
Rozwiązanie:
Jeśli liczba jest razy większa od liczby , to: .
Jeśli liczba jest razy większa od liczby , to .
Wobec tego otrzymujemy:
.
Zatem:
.
Wynika z tego, że .
Zapoznaj się z animacją pokazującą przykłady zastosowania porównywania ilorazowego liczb. Spróbuj najpierw samodzielnie wykonać proponowane tam zadania, a następnie porównaj z rozwiązaniami.

Film dostępny pod adresem /preview/resource/RIcF1psvfhu74
Animacja przedstawia jak porównywać liczby naturalne za pomocą ilorazu.
Jeżeli wiadomo, że , to liczba jest 1. mniejsza, 2. większa, 3. równa od .
Jeżeli wiadomo, że , to liczba jest 1. mniejsza, 2. większa, 3. równa .
Jeżeli liczby porządkujemy 1. najmniejszej, 2. , 3. , 4. , 5. największej, 6. więcej, 7. rosnąco, 8. mniej, to ustawiamy te liczby w kolejności od najmniejszej do największej.
Z dwóch liczb naturalnych większa jest ta liczba, która ma 1. najmniejszej, 2. , 3. , 4. , 5. największej, 6. więcej, 7. rosnąco, 8. mniej cyfr.
Liczba 1. najmniejszej, 2. , 3. , 4. , 5. największej, 6. więcej, 7. rosnąco, 8. mniej jest mniejsza od każdej liczby naturalnej dodatniej.
Wybierz.
2, 3, wyższy, niższy, 4, niższy, wyższy, 4, 2, 3
Jeżeli jeden obiekt jest 2 razy wyższy od drugiego, to ten drugi jest .............. razy .............. od pierwszego.
Jeżeli jeden obiekt jest 2 razy niższy od drugiego, to ten drugi jest .............. razy .............. od pierwszego.
Masz do dyspozycji jednakowych klocków. Ułóż z tych klocków dwie wieże, tak aby jedna z nich była razy wyższa od drugiej. Z ilu klocków może być zbudowana każda z tych wież?
Nie musisz wykorzystać wszystkich klocków.
Spróbuj wykorzystać jak najwięcej klocków.
Wieża zbudowana jest z klocków.
Wieża zbudowana jest z klocków. Wieża razy niższa będzie zbudowana z 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. , 17. , 18. , 19. , 20. , 21. , 22. , 23. , 24. , 25. , 26. , 27. , 28. , 29. , 30. , 31. , 32. , 33. , 34. , 35. , 36. , 37. , 38. , 39. , 40. , 41. , 42. , 43. , 44. , 45. , 46. , 47. , 48. , 49. , 50. , 51. , 52. , 53. , 54. , 55. klocków. Wieża razy wyższa będzie zbudowana z 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. , 17. , 18. , 19. , 20. , 21. , 22. , 23. , 24. , 25. , 26. , 27. , 28. , 29. , 30. , 31. , 32. , 33. , 34. , 35. , 36. , 37. , 38. , 39. , 40. , 41. , 42. , 43. , 44. , 45. , 46. , 47. , 48. , 49. , 50. , 51. , 52. , 53. , 54. , 55. klocków.
Wieża zbudowana jest z klocków. Wieża razy wyższa będzie zbudowana z 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. , 17. , 18. , 19. , 20. , 21. , 22. , 23. , 24. , 25. , 26. , 27. , 28. , 29. , 30. , 31. , 32. , 33. , 34. , 35. , 36. , 37. , 38. , 39. , 40. , 41. , 42. , 43. , 44. , 45. , 46. , 47. , 48. , 49. , 50. , 51. , 52. , 53. , 54. , 55. klocków. Wieża razy wyższa będzie zbudowana z 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. , 17. , 18. , 19. , 20. , 21. , 22. , 23. , 24. , 25. , 26. , 27. , 28. , 29. , 30. , 31. , 32. , 33. , 34. , 35. , 36. , 37. , 38. , 39. , 40. , 41. , 42. , 43. , 44. , 45. , 46. , 47. , 48. , 49. , 50. , 51. , 52. , 53. , 54. , 55. klocków.
Wieża zbudowana jest z klocków. Wieża razy wyższa będzie zbudowana z 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. , 17. , 18. , 19. , 20. , 21. , 22. , 23. , 24. , 25. , 26. , 27. , 28. , 29. , 30. , 31. , 32. , 33. , 34. , 35. , 36. , 37. , 38. , 39. , 40. , 41. , 42. , 43. , 44. , 45. , 46. , 47. , 48. , 49. , 50. , 51. , 52. , 53. , 54. , 55. klocków. Wieża razy niższa będzie zbudowana z 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. , 17. , 18. , 19. , 20. , 21. , 22. , 23. , 24. , 25. , 26. , 27. , 28. , 29. , 30. , 31. , 32. , 33. , 34. , 35. , 36. , 37. , 38. , 39. , 40. , 41. , 42. , 43. , 44. , 45. , 46. , 47. , 48. , 49. , 50. , 51. , 52. , 53. , 54. , 55. klocków.
Mamy jednakowe klocki. Budujemy z nich wieże. Jeden poziom wieży to jeden klocek. Wybierz odpowiednią liczbę.
80, 100, 41, 19, 16, 100, 71, 45, 20, 8, 24, 10, 3, 80, 8, 7, 17, 3, 12, 90, 60, 80, 51, 60, 16, 6, 50, 90, 9, 80, 70, 10, 30, 4, 70, 90, 100, 2, 19, 20, 13, 3, 17, 13, 3, 20, 13, 4, 40, 45, 6, 50, 100, 16, 4, 60, 7, 19, 7, 0, 7, 30, 20, 90, 4, 30, 70, 41, 12, 10, 30, 10, 40, 1, 4, 41, 50, 40, 5, 13
a) Wieża zbudowana jest z 56 klocków. Wieża 7 razy niższa będzie zbudowana z ............ klocków.
Wieża 8 razy niższa będzie zbudowana z ............ klocków.
b) Wieża zbudowana jest z 12 klocków. Wieża 4 razy niższa będzie zbudowana z ............ klocków.
Wieża 2 razy wyższa będzie zbudowana z ............ klocków.
c) Wieża zbudowana jest z 10 klocków. Wieża 3 razy wyższa będzie zbudowana z ............ klocków.
Wieża 2 razy wyższa będzie zbudowana z ............ klocków.
d) Wieża zbudowana jest z 8 klocków. Wieża 5 razy wyższa będzie zbudowana z ............ klocków.
Wieża 2 razy niższa będzie zbudowana z ............ klocków.
Porównaj liczbę czerwonych i zielonych serduszek na poniższych grafikach.
RQRxlzWYPNFZF1  Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RIg5CeZHXHYmd1  Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RT0PWxGQ4a0IG1  Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1AzYOBKTDDT81  Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Najmniejsza liczba trzycyfrowa jest 1. , 2. , 3. , 4. , 5. , 6. , 7. razy mniejsza od najmniejszej liczby czterocyfrowej.
Największa liczba dwucyfrowa jest równa iloczynowi liczby i liczby 1. , 2. , 3. , 4. , 5. , 6. , 7. .
Najmniejsza liczba czterocyfrowa jest 1. , 2. , 3. , 4. , 5. , 6. , 7. razy większa od liczby .
W sadzie rośnie jabłoni, razy więcej śliw oraz o więcej grusz niż śliw. Oblicz:
ile razy mniej jest jabłoni niż grusz,
ile razy więcej jest grusz niż śliw.
Wiadomo, że przy dzieleniu liczby przez otrzymujemy reszty , przy dzieleniu liczby przez otrzymujemy reszty , a przy dzieleniu liczby przez otrzymujemy reszty . Oblicz:
ile razy liczba jest większa od liczby
ile razy liczba jest mniejsza od liczby .
Słownik
wynik dzielenia liczb, jedno z podstawowych działań arytmetycznych
Notatnik
Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.
