Własności figur geometrycznych na płaszczyźnie
10. Powtórzenie - własności figur geometrycznych na płaszczyźnie

Trudno znaleźć figury płaskie wokół nas, bowiem na ogół są one bryłami. Weźmy za przykład takie piramidy w Egipcie, czy Piramidę Luwru. To bryły. Gdyby tak jednak spojrzeć na nie z przodu… zobaczymy zwyczajny trójkąt.

Dodatkowo możemy również patrzeć na otaczający nas świat z góry – Internet nam to umożliwia. I gdy dla przykładu przyjrzymy się siedzibie Departamentu Obrony Stanów Zjednoczonych czyli Pentagonowi, zobaczymy pięciokąt (na co sama nazwa wskazuje).
W tej lekcji powtórzymy i utrwalimy wiadomości dotyczące figur.
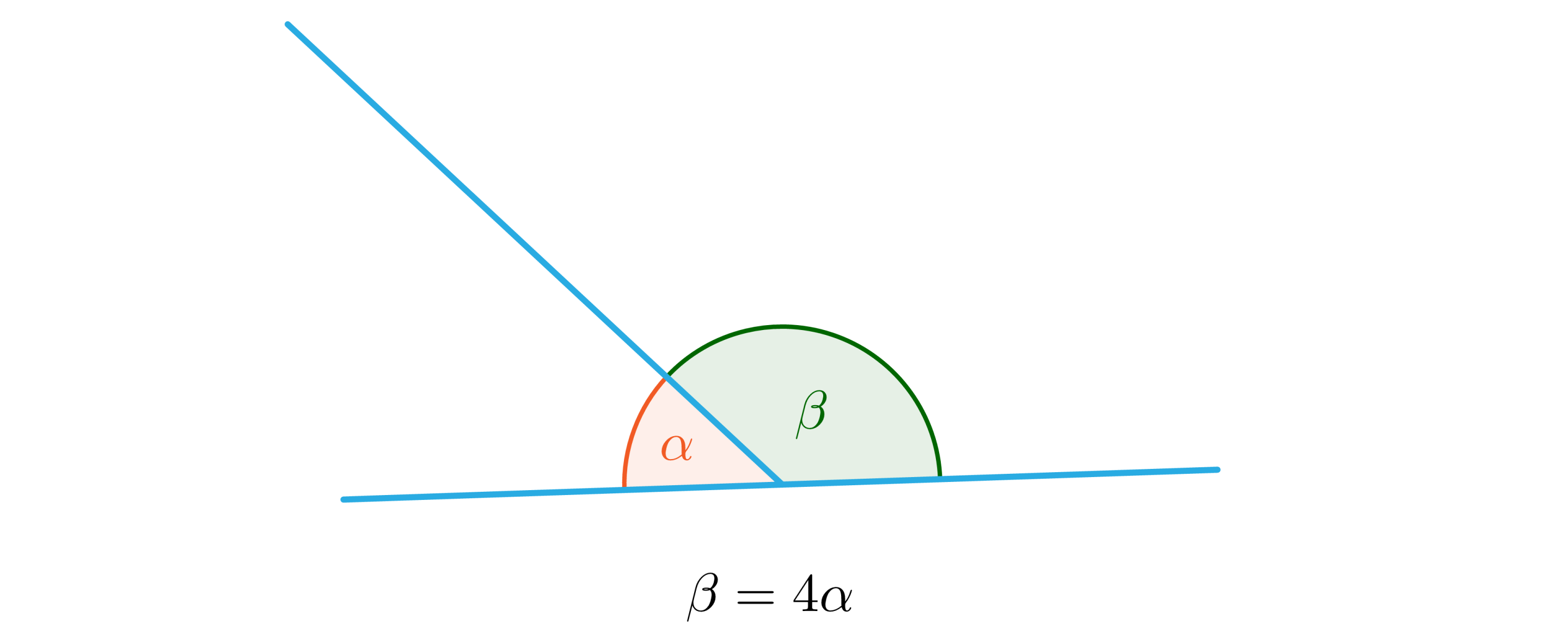
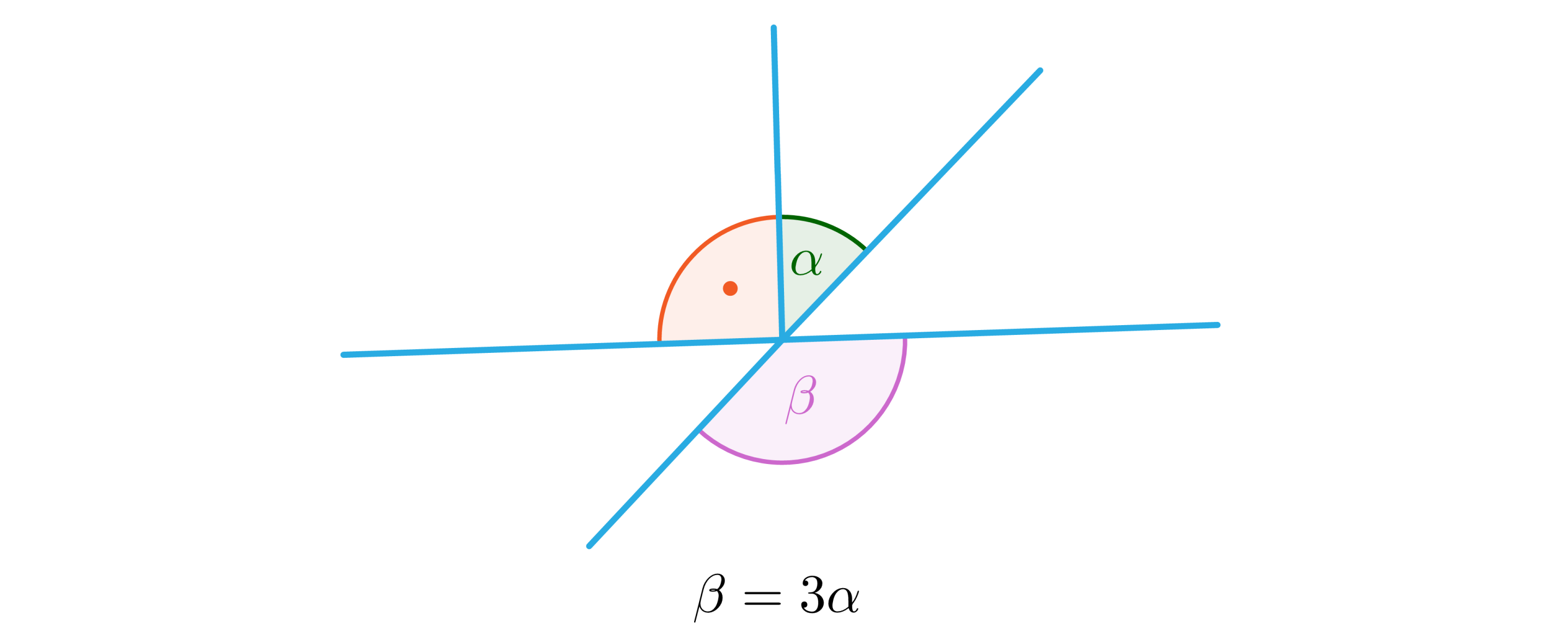
Zapoznaj się z poniższym rysunkiem. Oblicz miarę kąta .

Korzystając z informacji opisujących zależność między i , wybierz poprawną odpowiedź.
Rozwiąż test składający się z trzech pytań.
Zaznacz prawidłową odpowiedź. Możliwe odpowiedzi: 1. , , 2. , , 3. , , 4. ,
Zaznacz prawidłową odpowiedź. Możliwe odpowiedzi: 1. , , 2. , , 3. , , 4. ,
Zaznacz prawidłową odpowiedź. Możliwe odpowiedzi: 1. , , 2. , , 3. , , 4. ,
Na rysunkach przecinające się proste tworzą trójkąt. Jakie miary mają kąty i ? Ile wynosi suma miar kątów w utworzonym trójkącie?

............
............
Suma miar kątów w trójkącie wynosi .............
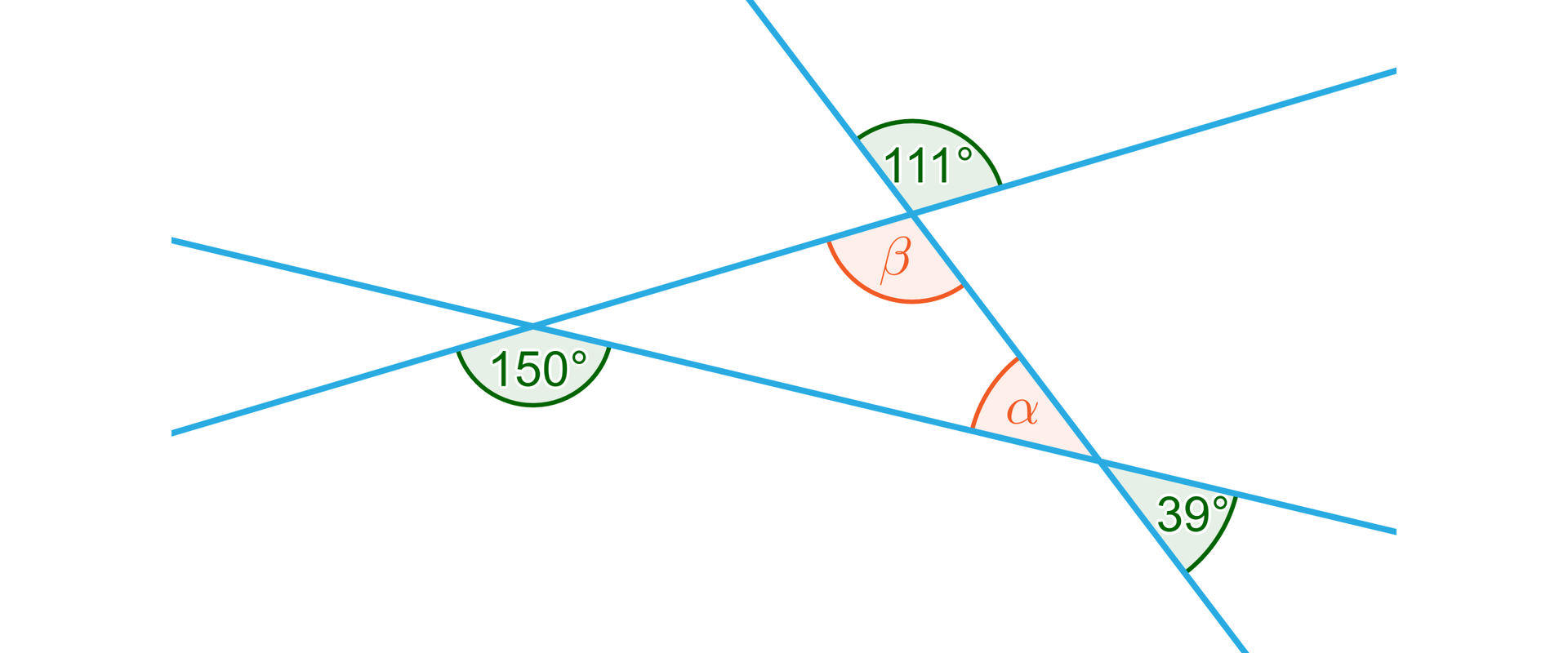
............
............
Suma miar kątów w trójkącie wynosi .............
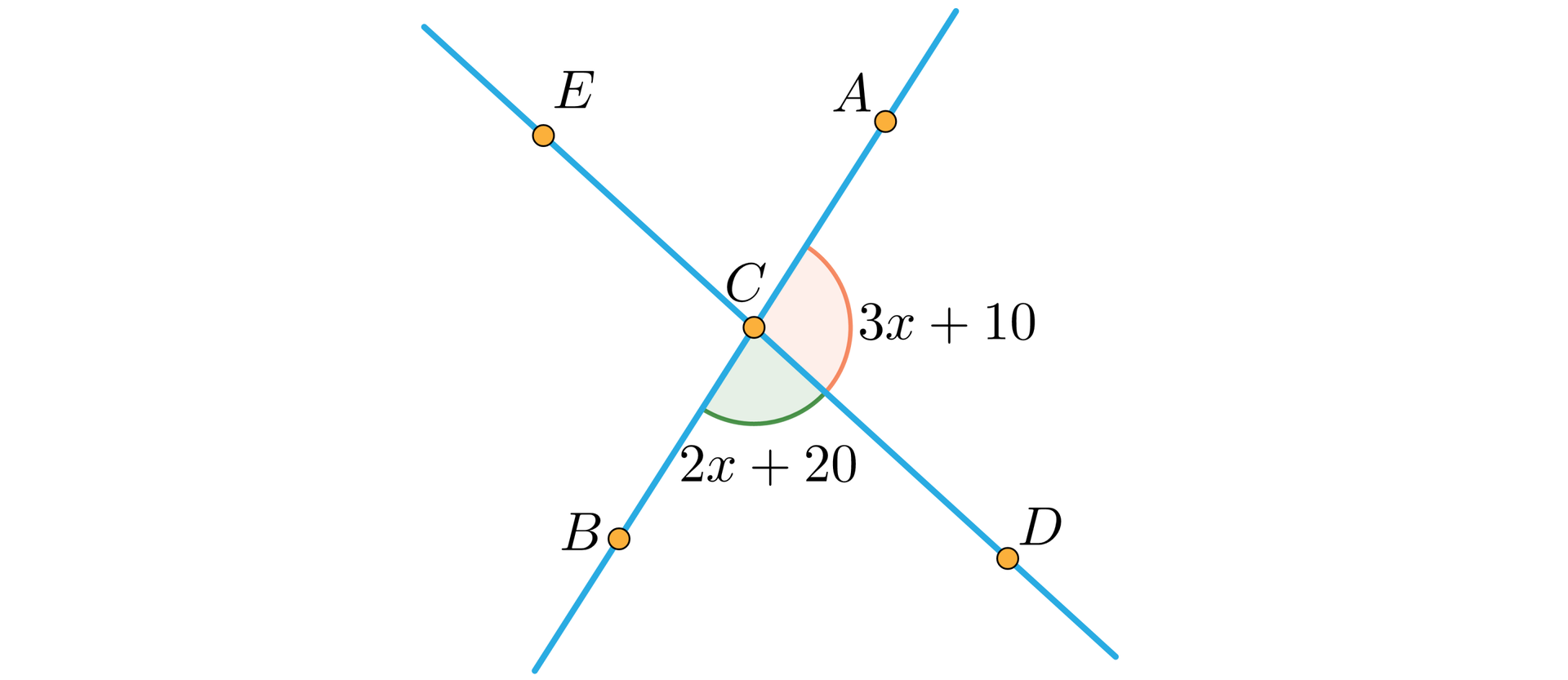
Na rysunku przedstawione są dwie przecinające się proste oraz wyrażenia algebraiczne ze zmienną opisujące miarę kątów w stopniach. Wyznacz miary kątów wypukłych i .
Ile różnych prostokątów można utworzyć z przystających kwadratów? Który z tych prostokątów będzie miał najmniejszy obwód?
Trapezy równoramienne i są przystające. Oblicz obwód trapezu .

Wykaż, że jeśli dwa trójkąty równoboczne mają równe wysokości, to są przystające.
Uzasadnij, że pole równoległoboku jest czterokrotnie większe od pola trójkąta .

Zapoznaj się z poniższą ilustracją, która przedstawia dwa trójkąty przystające.

Pole trójkąta jest równe .
Podstawa trójkąta ma długość . Oblicz długość wysokości poprowadzonej do tej podstawy.
Wysokość trójkąta jest równa . Oblicz długość podstawy trójkąta, na którą poprowadzono tę wysokość.
Dokończ zdanie, wybierając poprawną odpowiedź.
Wynika z tego, że średnia arytmetyczna długości wszystkich boków trójkąta jest równa: Możliwe odpowiedzi: 1. , 2. , 3. , 4.
Zapoznaj się z poniższym rysunkiem i oblicz długość w każdym rombie. Uzupełnij luki w zdaniach, wpisując odpowiednią liczbę.

Dany jest okrąg o środku w punkcie i promieniu , gdzie jest liczbą naturalną dodatnią. Z punktu leżącego poza okręgiem poprowadzono styczne do okręgu, przecinające się pod kątem . Ile wynosi długość odcinka ? Rozważ dwa przypadki.
Metalowy element ozdobny ma kształt trapezu przedstawionego na rysunku. Ile blachy potrzeba na jego wykonanie?

Zapoznaj się z poniższym rysunkiem, na którym znajdują się trzy trapezy.

Notatnik
Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.