Własności figur geometrycznych na płaszczyźnie
9. Dowody geometryczne
W tym materiale dowiesz się, w jaki sposób można uzasadniać pewne stwierdzenia matematyczne. Zadania na dowodzenie łatwo jest poznać, bo zaczynają się zwykle od sformułowań Wykaż, że….
, Uzasadnij, że…
, Udowodnij, że…
. Wykazywanie prawdziwości stwierdzeń (zwanych w matematyce twierdzeniami) często sprawia kłopot, choć problemy tam zawarte nie muszą być trudne. Istnieje wiele reguł postępowania, które pomagają w dowodzeniu twierdzeń matematycznych. Niektóre z nich poznamy.
Twierdzenia matematyczne składają się z dwóch części – założenia i tezy. W części zwanej założeniemzałożeniem zapisane jest to, co jest dane, podane są też warunki, przy których spełnione jest twierdzenie.
W drugiej części twierdzenia (w tezie) zawarta jest własność, która zachodzi, gdy spełnione są warunki opisane w założeniu.
Nie każde stwierdzenie jest prawdziwe. Na przykład stwierdzenie: jeżeli trójkąt jest prostokątny, to ma dwa kąty proste, jest fałszywe. Stwierdzenie (hipoteza) staje się twierdzeniem, gdy je udowodnimy. Aby udowodnić hipotezę, nie wystarczy pozytywna weryfikacja dla kilku, kilkuset czy nawet kilku milionów przypadków. Dowód musi uzasadnić hipotezę w całej ogólności. Aby natomiast stwierdzić, że hipoteza nie jest prawdziwa, wystarczy podać jeden kontrprzykład, tzn. przykład pokazujący, że przypuszczenie jest fałszywe.
Uzasadnimy, że hipoteza: jeżeli suma kątów czworokąta jest równa , to czworokąt ten jest prostokątem jest fałszywa.
Rozwiązanie:
Podajemy kontrprzykład: w trapezie suma kątów jest równa , a trapez nie musi być prostokątem.
Zatem hipoteza jest fałszywa. Stwierdzenie: jeżeli suma kątów czworokąta jest równa , to czworokąt ten jest prostokątem nie jest twierdzeniem matematycznym.
Dowód twierdzenia zawiera kolejne czynności, które wykonujemy, aby uzasadnić prawdziwość tezy.
Najczęstsze rodzaje dowodów, to dowód wprostdowód wprost oraz dowód nie wprost.
Dowód wprostDowód wprost – prawdziwość tezy jest dowodzona bezpośrednio z założeń twierdzenia, wcześniej udowodnionych twierdzeń, ustalonych reguł postępowania.
Na początek pokażemy, w jaki sposób można udowodnić twierdzenia związane z kątami wielokątów.
Udowodnimy, że dwusieczna kąta wewnętrznego trójkąta i dwusieczna kąta zewnętrznego przy tym samym wierzchołku są prostopadłe.
Dowód wprostDowód wprost
Wykonajmy najpierw rysunek pomocniczy.
Rysujemy dowolny trójkąt . Wybieramy jeden z wierzchołków trójkąta, na przykład wierzchołek . Na prostej obieramy dowolny punkt, leżący poza odcinkiem , bliżej punktu niż i nazywamy go .
Rysujemy dwusieczną kąta i dwusieczną kąta zewnętrznego do tego kąta (czyli kąta przyległego do kąta , a więc kąta ).
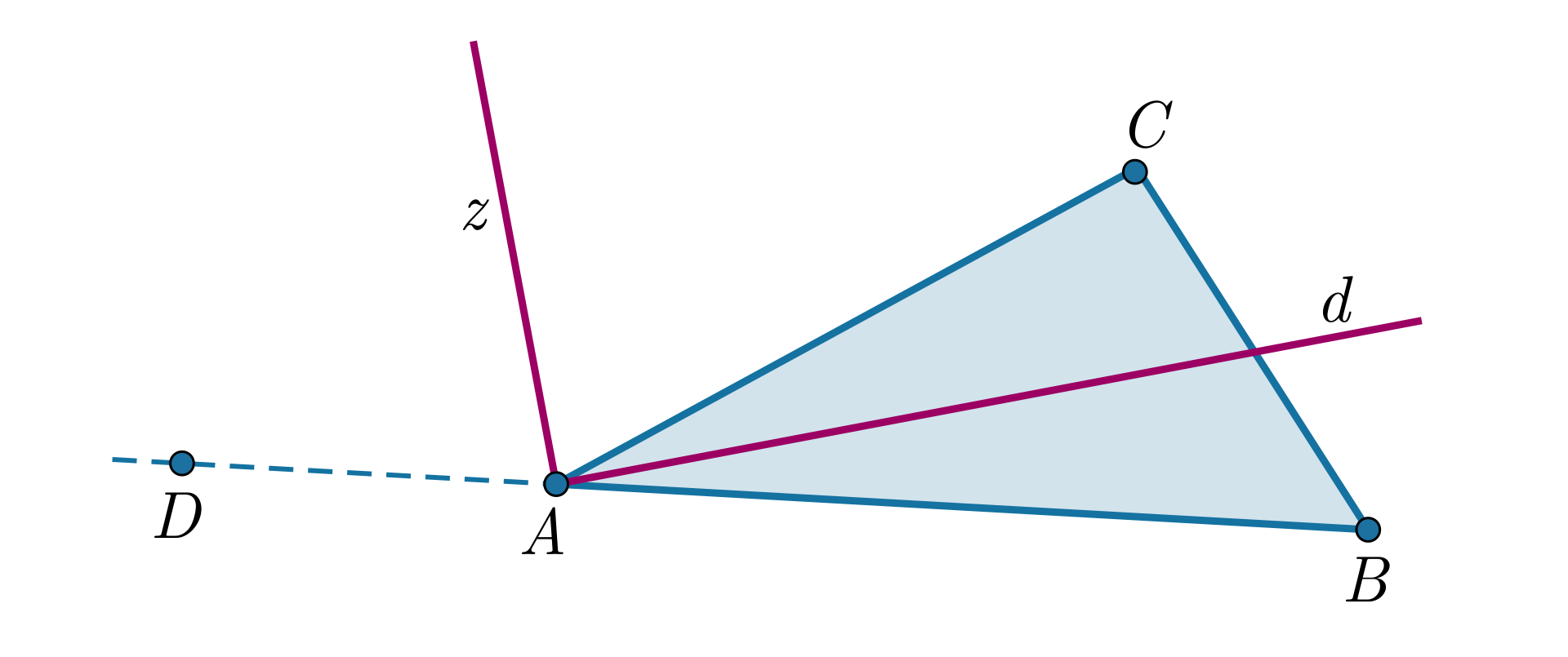
Oznaczmy przez miarę kąta . Półprosta dzieli kąt na dwa kąty równe, każdy o mierze .
Oznaczmy przez miarę kąta . Półprosta dzieli kąt na dwa kąty równe, każdy o mierze .
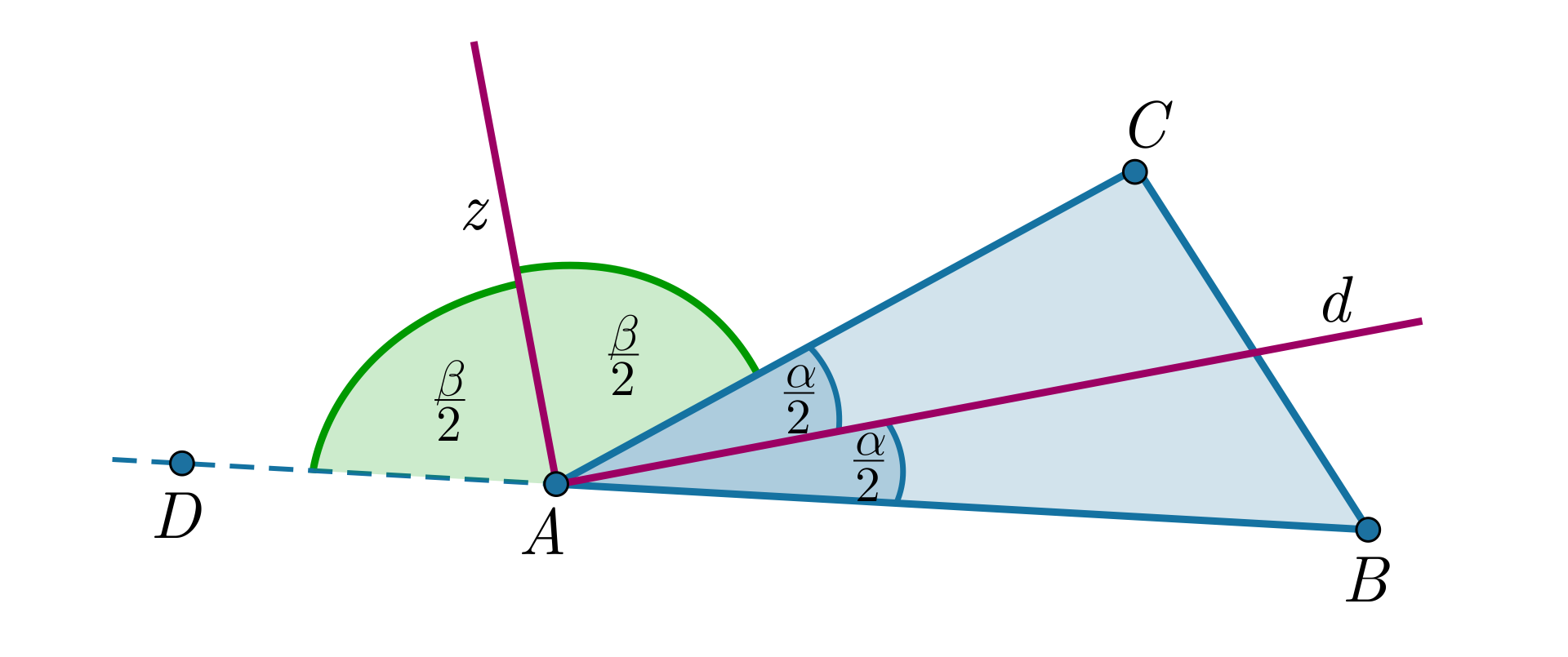
Kąt i kąt to kąty przyległe, zatem suma ich miar jest równa .
Dzielimy obie strony równości przez .
Stąd
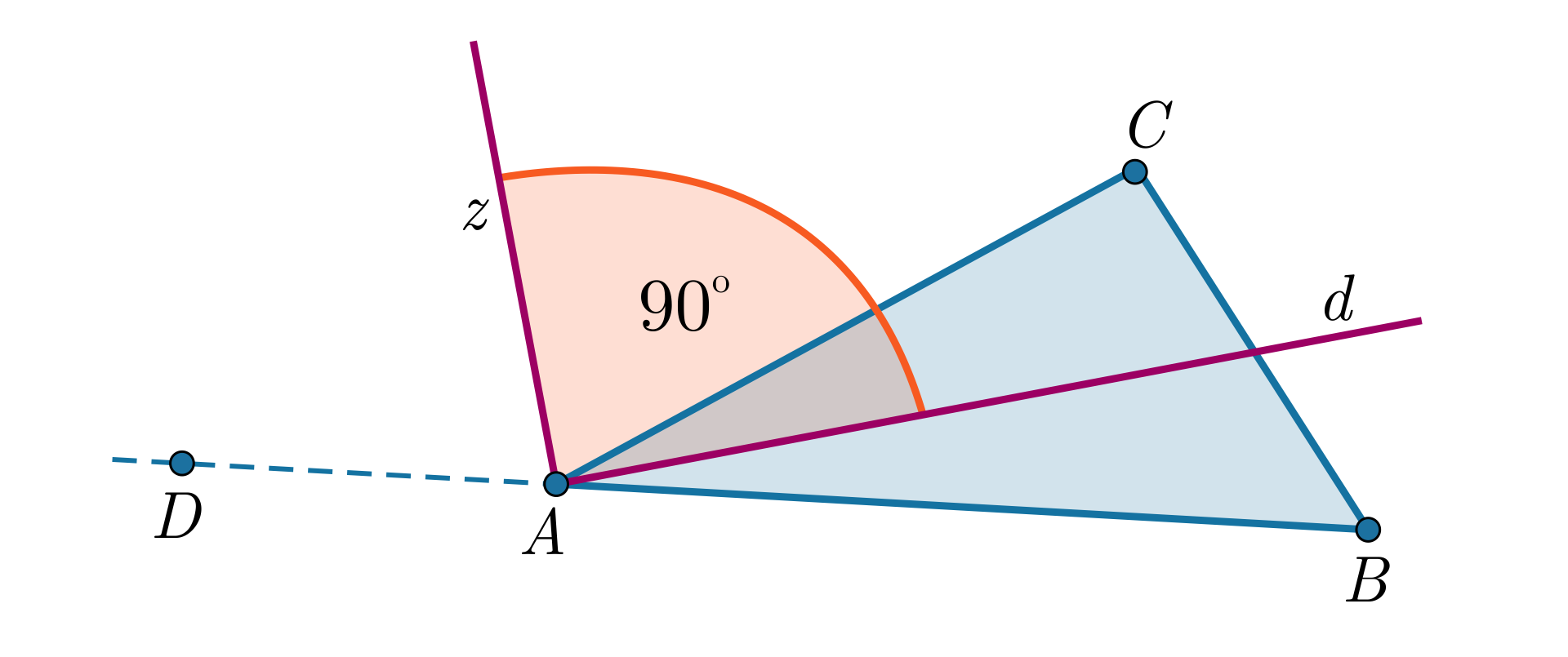
Oznacza to, że kąt między dwusiecznymi jest prosty, a więc dwusieczne są prostopadłe.
W następnym przykładzie udowodnimy kolejną własność związaną z kątami zewnętrznymi.
Udowodnimy, że suma miar wszystkich kątów zewnętrznych trójkąta jest równa .
Dowód
Narysujmy dowolny trójkąt i oznaczmy jego kąty wewnętrzne odpowiednio przez , , .
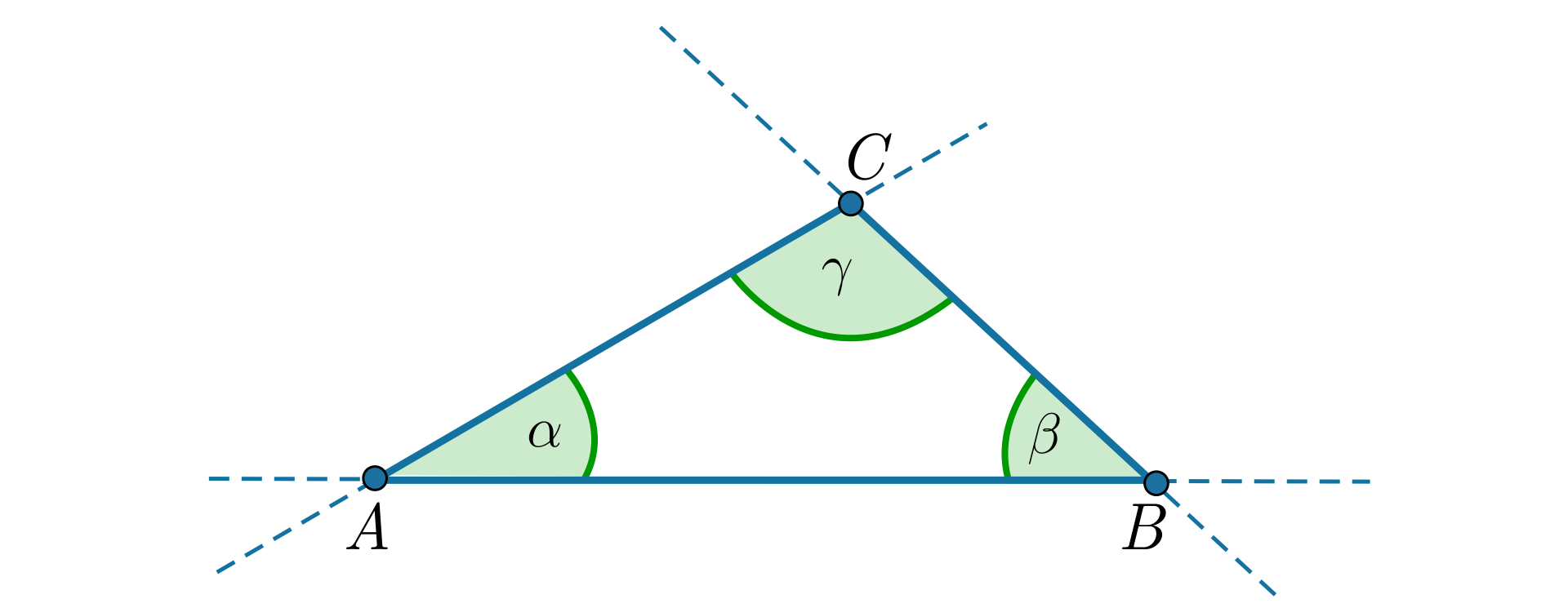
Każdy z kątów wewnętrznych trójkąta ma dwa kąty zewnętrzne – są to kąty przyległe do tego kąta wewnętrznego.
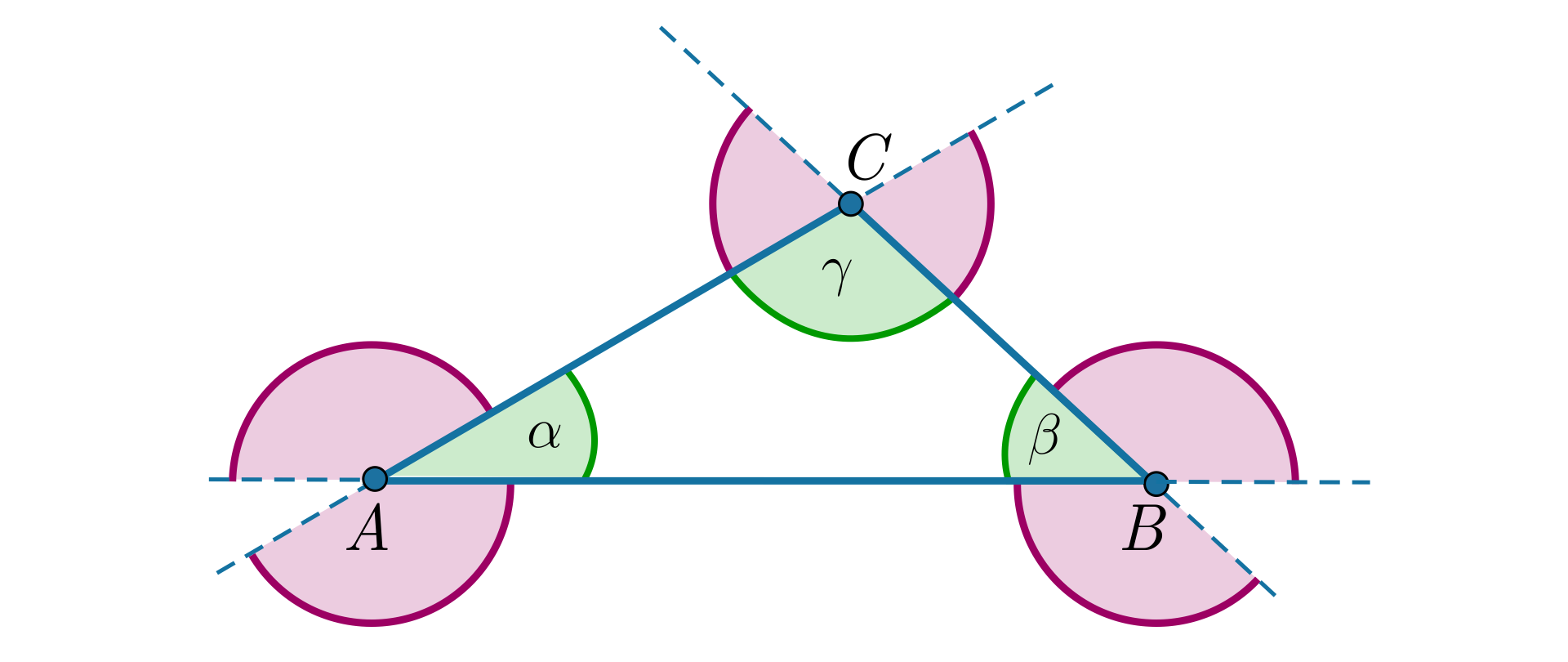
Kąty te mają odpowiednio miary: , , .
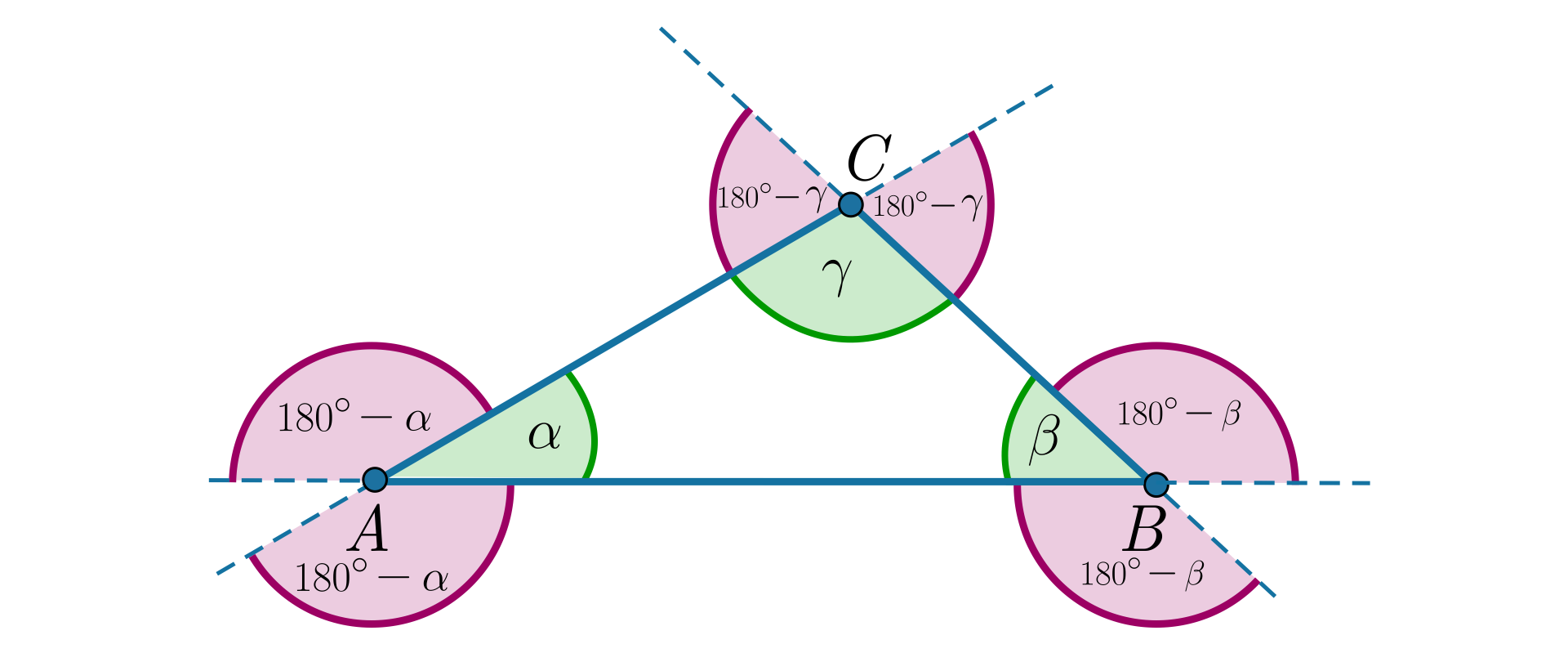
Suma miar wszystkich kątów zewnętrznych jest równa:
Ponieważ suma kątów wewnętrznych trójkąta jest równa , więc
Udowodniliśmy więc, że suma kątów zewnętrznych trójkąta jest równa .
W następnym przykładzie skorzystamy z własności trójkąta równoramiennego – w trójkącie równoramiennym kąty przy podstawie są równe. Skorzystamy też z własności równoległoboku – suma kątów przy jednym boku równoległoboku jest równa .
W równoległoboku bok jest dwa razy dłuższy od boku . Wierzchołki i tego równoległoboku połączono ze środkiem boku . Udowodnij, że kąt jest prosty.
Dowód
Oznaczmy:
, - długości boków równoległoboku .
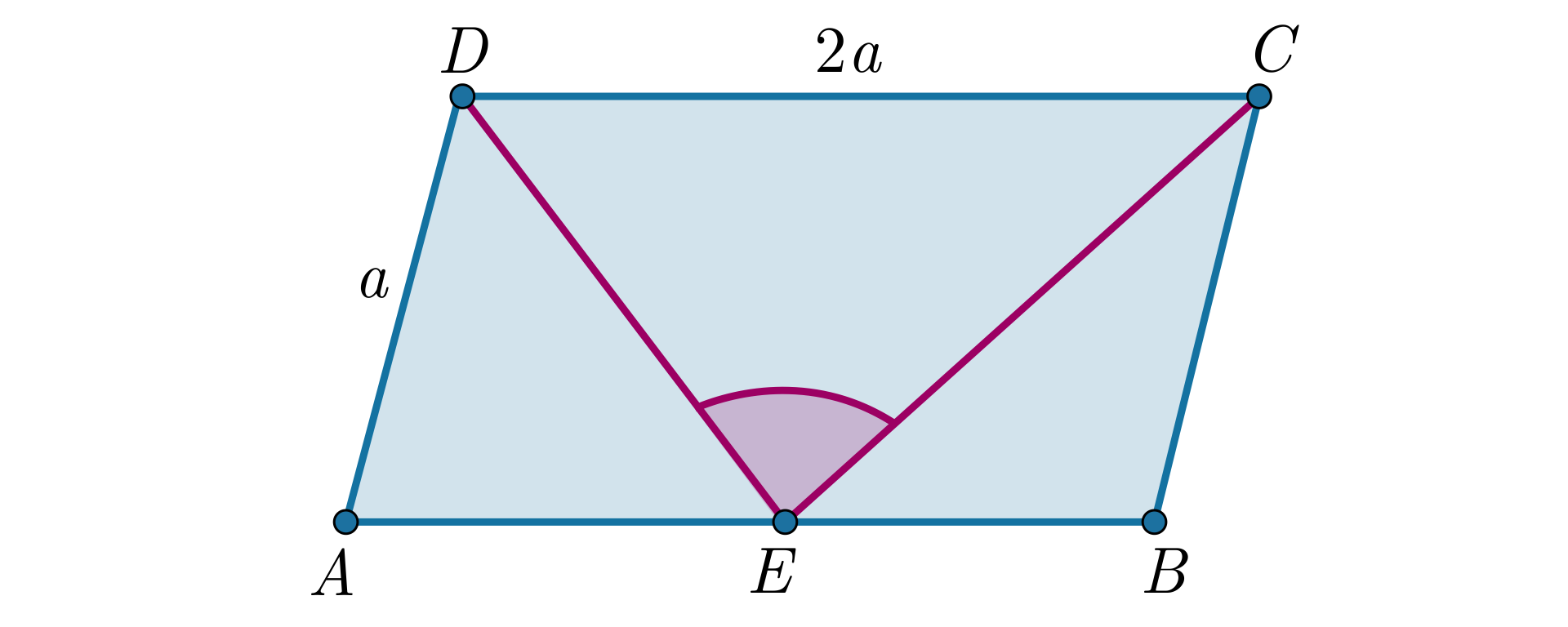
Ponieważ punkt jest środkiem boku , więc
Wynika z tego, że trójkąty i są równoramienne. Zatem kąty przy podstawie trójkąta są równe. Również kąty przy podstawie trójkąta są równe.
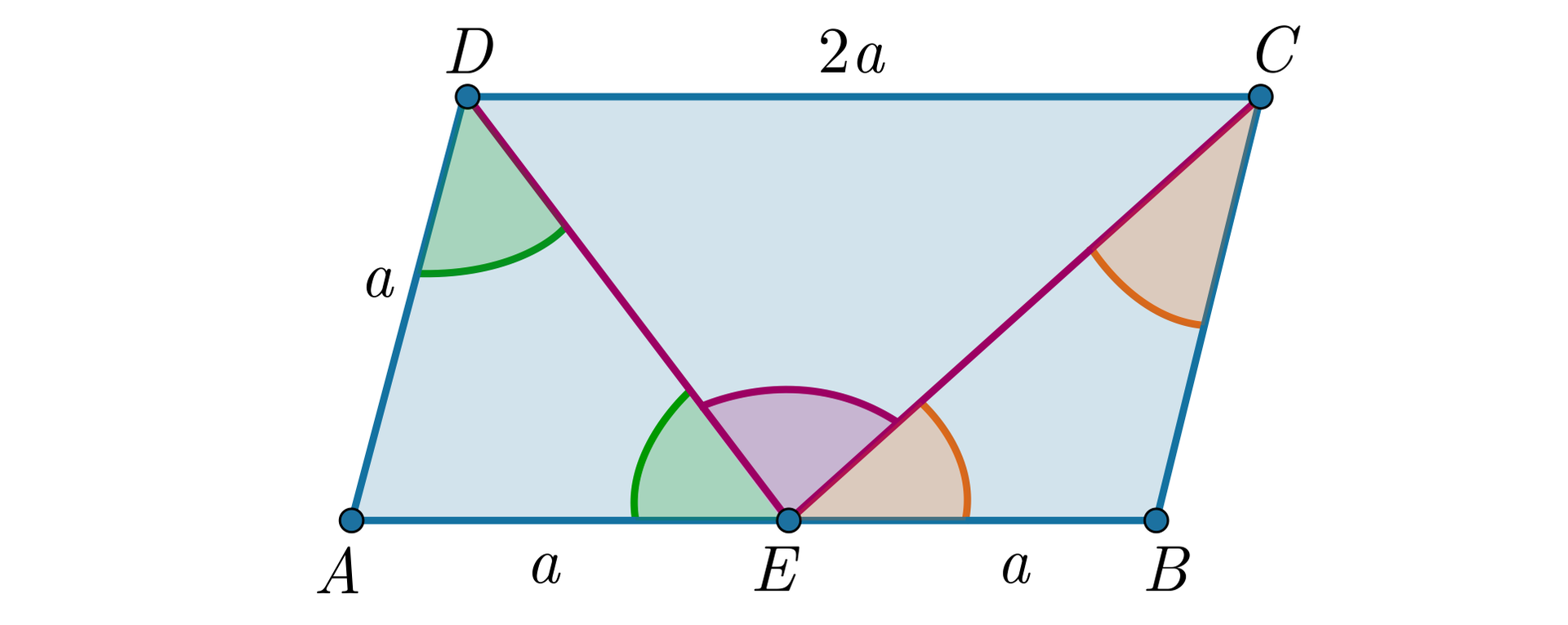
Oznaczmy przez miarę kąta . Wtedy:
Ponieważ
zatem
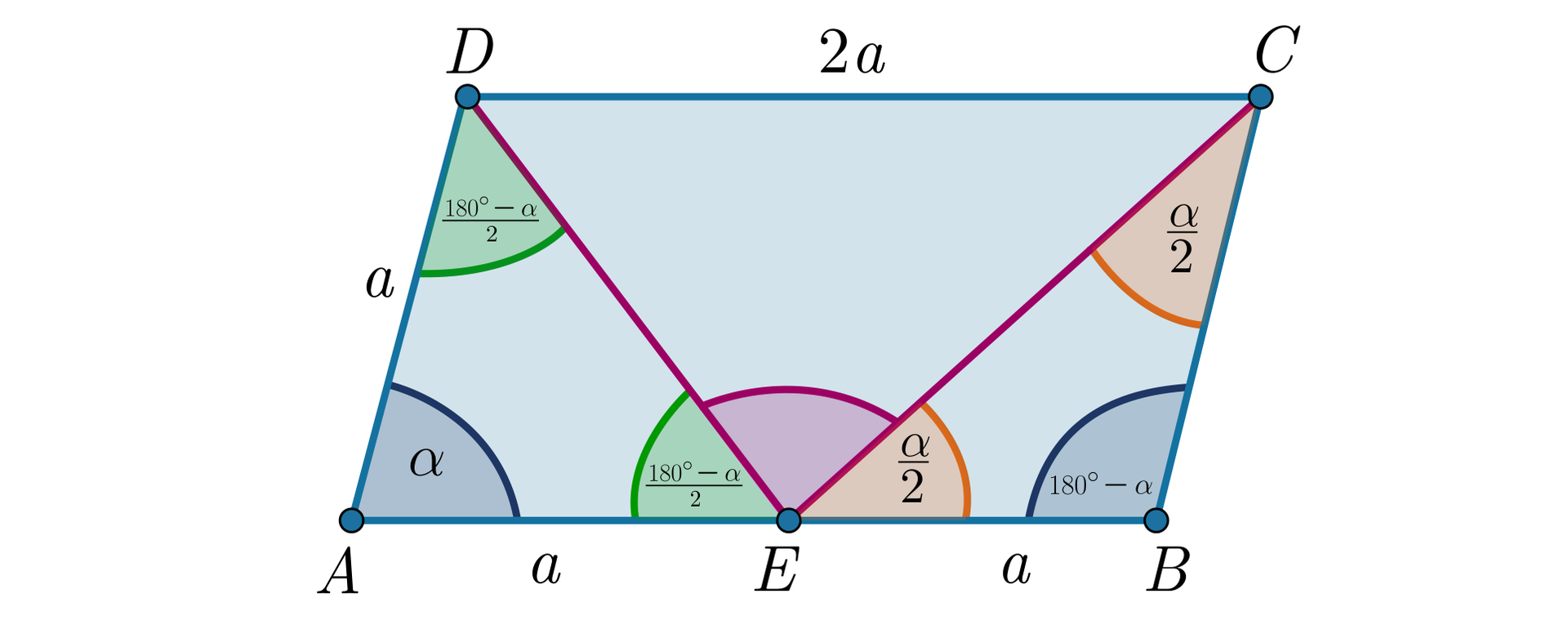
Suma kątów , , jest równa kątowi półpełnemu.
Stąd
Wynika z tego, że kąt jest prosty, co należało udowodnić.
Udowodnimy teraz znaną własność przekątnych kwadratu. Własność tę możemy wykazać w różny sposób – my zastosujemy twierdzenie Pitagorasa. Tym razem zapiszemy najpierw założeniezałożenie oraz tezę i przejdziemy dopiero do dowodu.
Udowodnimy, że jeżeli czworokąt jest kwadratem, to jego przekątne mają równe długości.
ZałożenieZałożenie: czworokąt jest kwadratem.
TezaTeza: przekątne czworokąta mają równe długości.
Dowód
Czworokąt jest kwadratem, zatem ma wszystkie boki równe.
Oznaczmy:
– długość boku czworokąta .
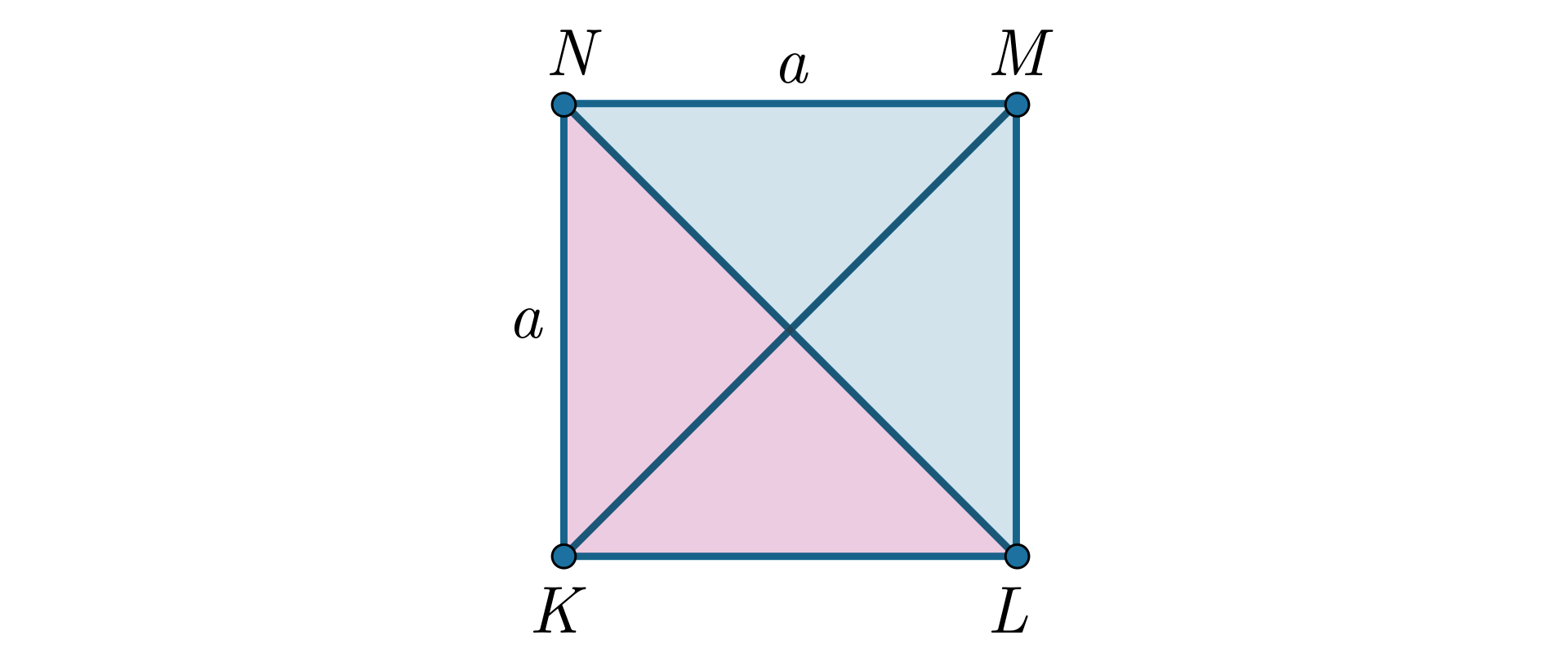
Trójkąt jest prostokątny. Aby obliczyć jego przeciwprostokątną , skorzystamy z twierdzenia Pitagorasa.
Trójkąt jest prostokątny. Aby obliczyć jego przeciwprostokątną , skorzystamy z twierdzenia Pitagorasa.
Stąd wynika, że , co należało udowodnić.
W ostatnim przykładzie pokażemy zastosowanie dowodzenia twierdzeń w sytuacjach praktycznych.
Adam, Borys, Cezary, Dariusz i Edgar mieszkają w domach (oznaczonych odpowiednio , , , , ) położonych tak, jak na rysunku. Domy te łączą ulice takie, że , oraz kąt i kąt to kąty proste. Udowodnimy, że Adam mieszka tak samo daleko od Darka jak Borys od Edgara.
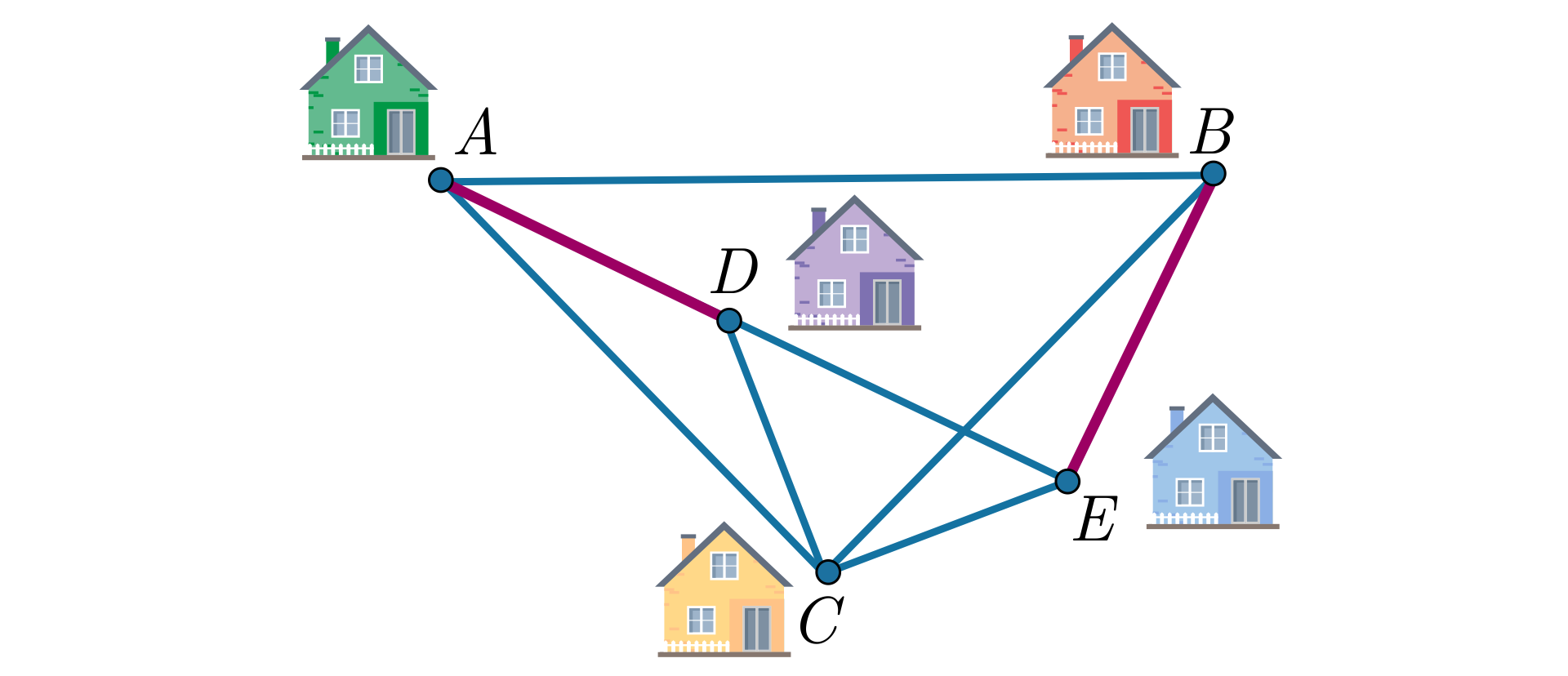
Na podstawie treści zadania wnioskujemy, że i .
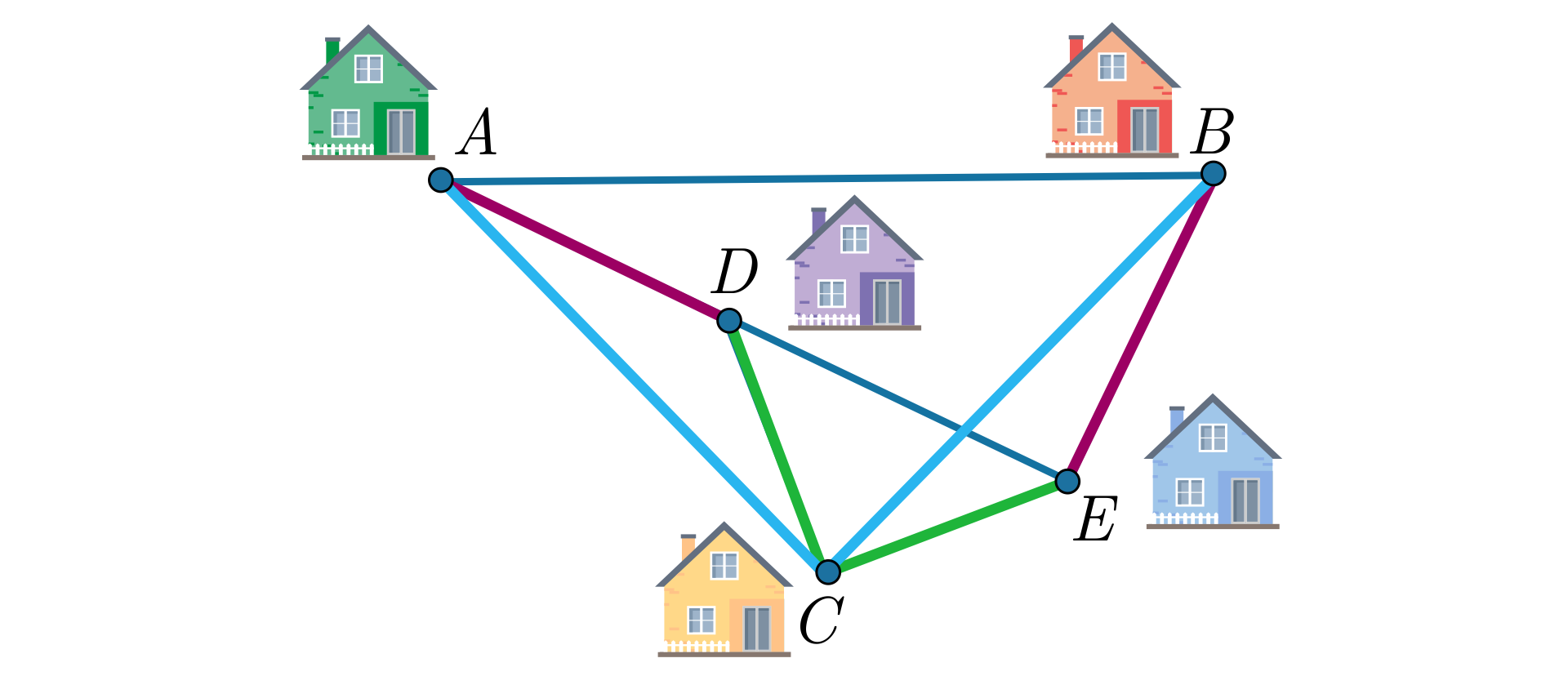
Zatem w trójkątach i mamy dwie pary boków o równych długościach. Aby ustalić, że również równe są boki i , uzasadnimy najpierw, że trójkąty i są przystające.
Oznaczmy:
– kąt ,
– kąt ,
– kąt .
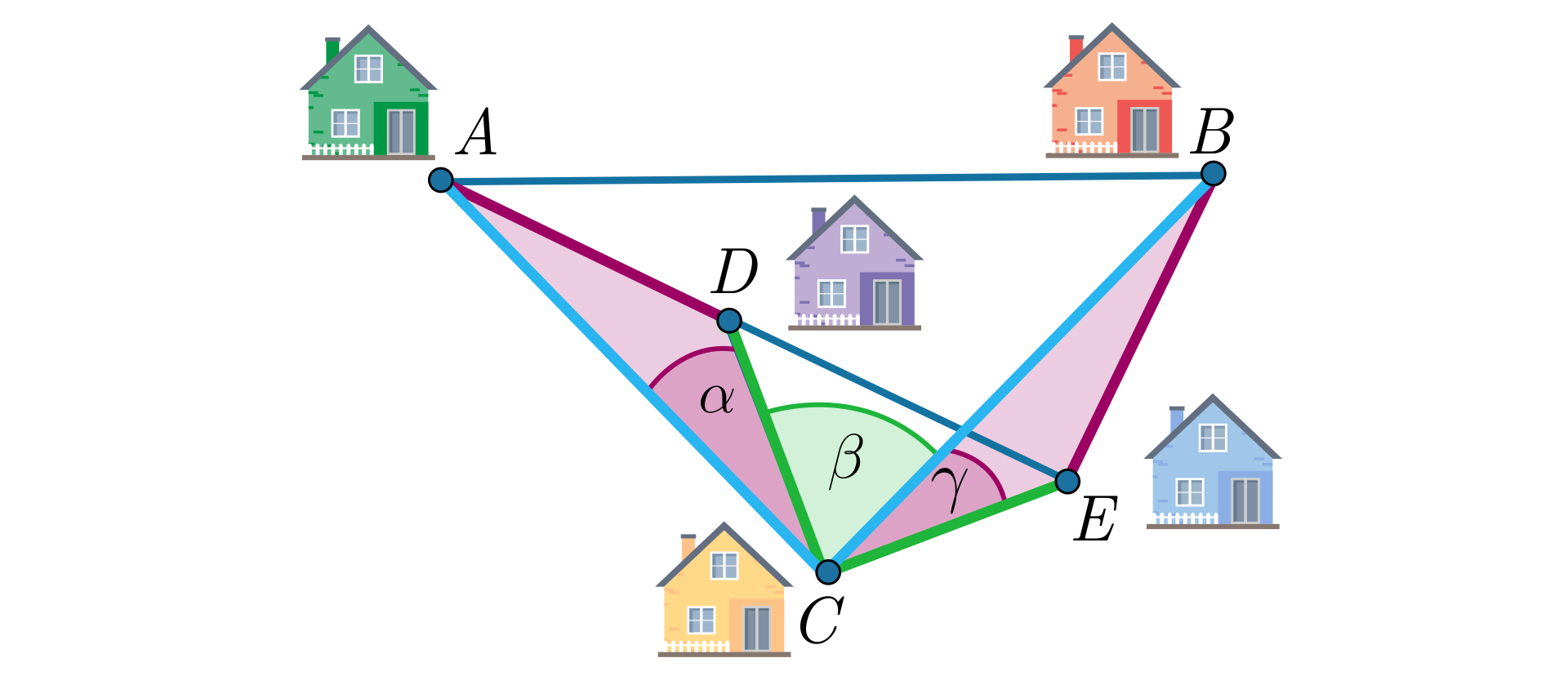
Ponieważ kąt jest prosty, zatem .
Kąt również jest prosty, więc .
Wynika z tego, że .
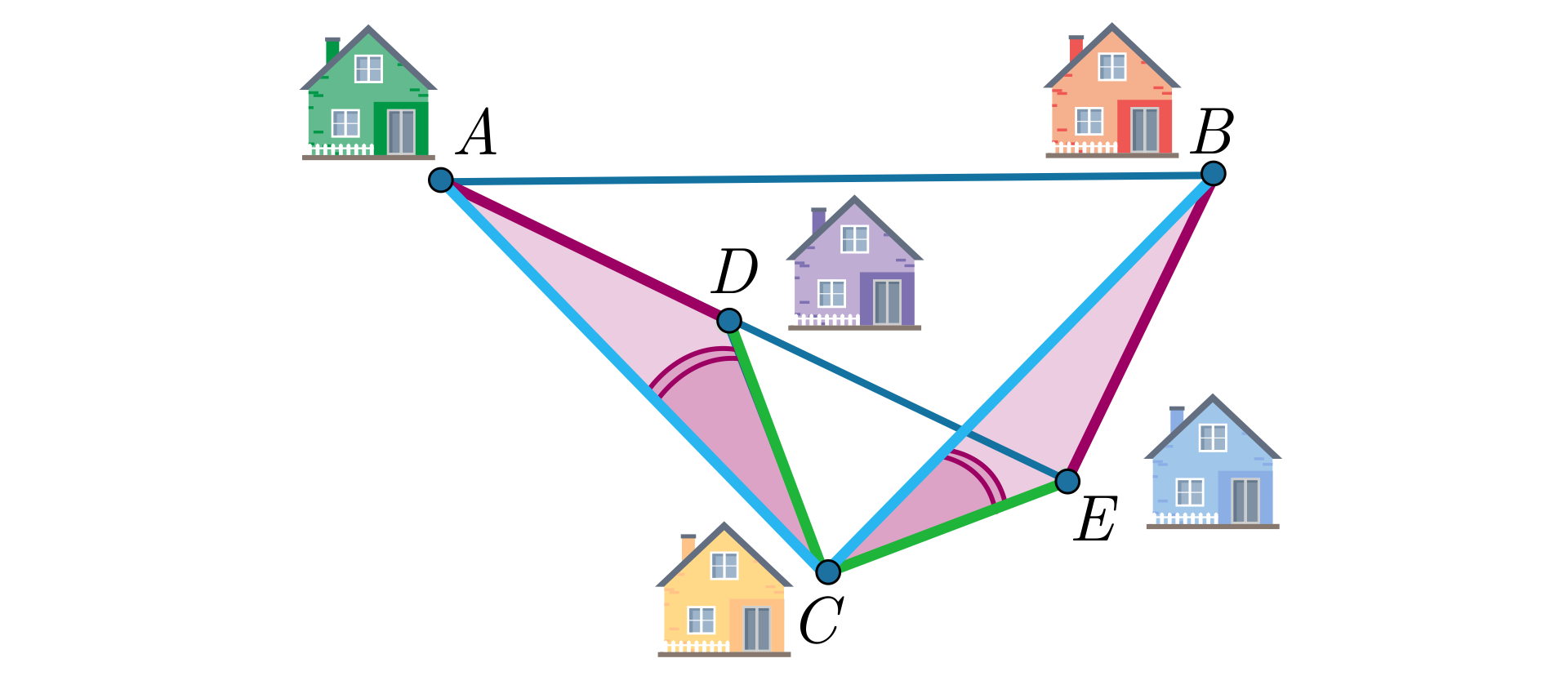
W trójkątach i odpowiednie dwa boki i kąt między nimi są równe. Na mocy cechy przystawania trójkątów bok – kąt – bok stwierdzamy, że trójkąty i są przystające. Mają więc odpowiednie boki równej długości, czyli .
Udowodniliśmy więc, że Adam mieszka tak samo daleko od Darka jak Borys od Edgara.
Animacja
Zapoznaj się z animacją, który przybliży ci zagadnienia związane z twierdzeniami i ich dowodami.
Zwróć uwagę na rodzaje twierdzeń i rodzaje dowodów.

Film dostępny pod adresem /preview/resource/R8E1EtFSWfwes
Animacja nawiązująca do treści materiału
Rozstrzygnij, czy hipoteza: każde dwa trójkąty prostokątne równoramienne są przystające jest prawdziwa.
Do twierdzenia: jeżeli każda krawędź prostopadłościanu ma długość , to ten prostopadłościan jest sześcianem podaj twierdzenie odwrotne i określ jego prawdziwość.
Prezentacja multimedialna
Zapoznaj się z prezentacją, w której zawarte są przykłady dowodzenia prostych związków miarowych w figurach płaskich i bryłach. Spróbuj najpierw samodzielnie rozwiązać każde zawarte tam zadanie, a następnie porównaj z rozwiązaniem.
Slajd pierwszy:
Lektor mówi: Zapoznaj się z dowodami kilku prostych związków miarowych w wielokątach oraz w znanych ci figurach przestrzennych.
Na filmie pokazana jest animacja figur przesuwających się po planszy.
Slajd drugi:
Lektor mówi: Przykład pierwszy. Udowodnimy teraz ciekawą własność trójkąta, która wynika bezpośrednio z warunku wiążącego długości boków trójkąta.
Na filmie pokazana jest treść zadania: Na boku trójkąta zaznaczono punkt . Udowodnimy, że .
Lektor mówi: Wykonujemy rysunek pomocniczy.
Na filmie pojawia się trójkąt . Na boku trójkąta zaznaczono punkt . Odrębnym kolorem zaznaczony jest trójkąt .
Lektor mówi: Skorzystamy z warunku budowy trójkąta. Rozpatrujemy trójkąt .
Na filmie pojawia się napis: Boki trójkąta spełniają nierówność: .
Lektor mówi: Rozpatrujemy trójkąt .
Na filmie na wcześniej narysowanym trójkącie podświetlają się boki , , tworząc trójkąt .
Lektor mówi: Dodajemy stronami zapisane nierówności.
Na filmie pokazane jest dodawanie pod kreską. Dodawane są dwie nierówności oraz . Otrzymany wynik, to .
Lektor mówi: Zauważmy, że suma odcinków i jest równa odcinkowi .
Na filmie pojawiają się obliczenia: stąd .
Lektor mówi: Od obu stron nierówności odejmujemy i otrzymujemy dowodzoną nierówność. Wykonujemy rysunek pomocniczy.
Na filmie pojawia się nierówność .
Slajd trzeci:
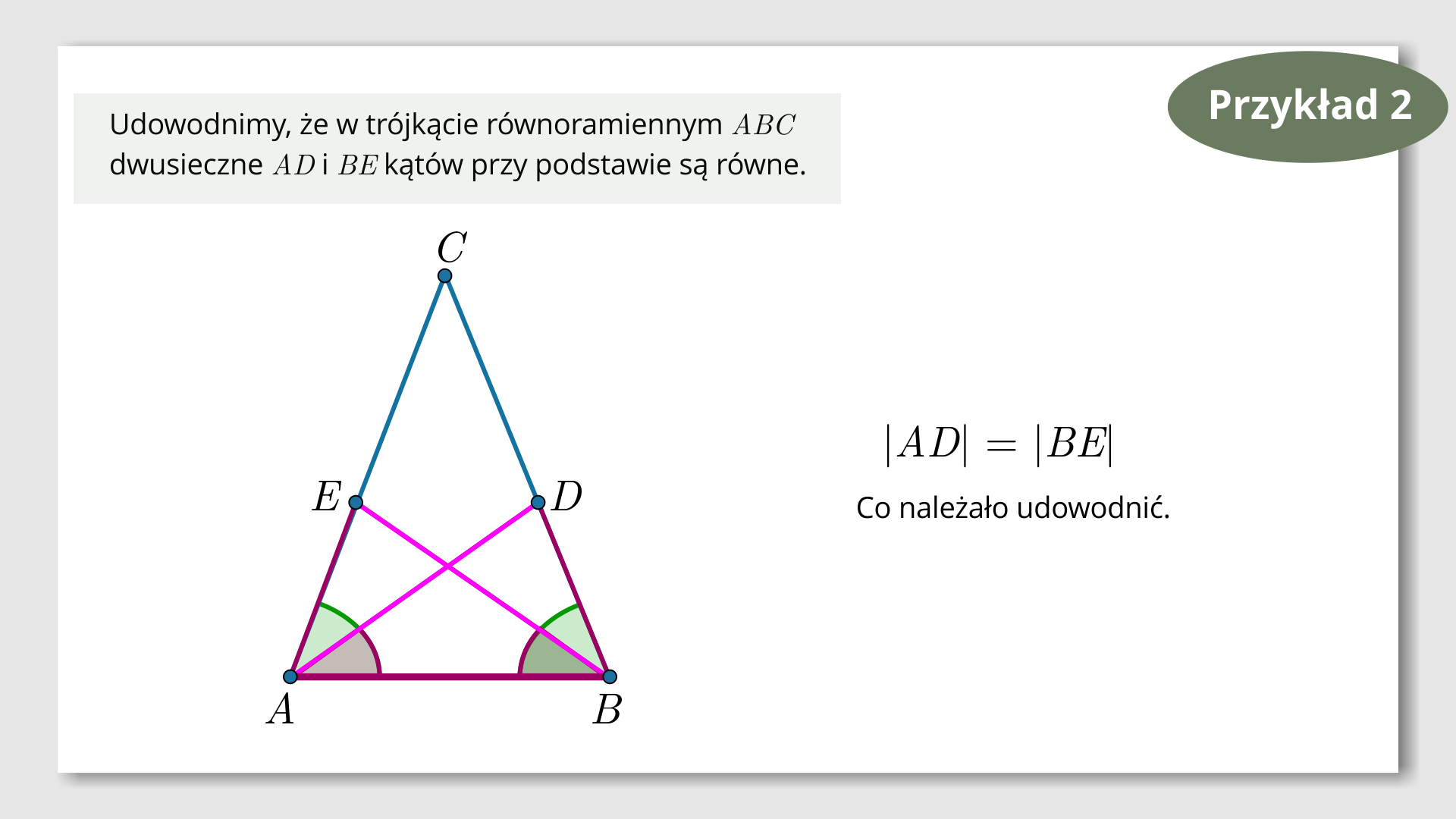
Lektor mówi: Przykład drugi. Udowodnimy teraz własność trójkąta równoramiennego, którą z reguły przyjmujesz jako oczywistą.
Na grafice interaktywnej pokazana jest treść zadania: Udowodnimy, że w trójkącie równoramiennym dwusieczne i kątów przy podstawie są równe. Pod treścią zadania jest narysowany trójkąt . Na bokach trójkąta i są zaznaczone odpowiednio punkty oraz tworząc dwusieczne i . Na grafice są dodane cztery punkty interaktywne, w których są ukyte treści.
Punkt pierwszy. Rozpatrujemy trójkąty i . Mają one wspólny bok . Dodana jest grafika trójkąta z wyróżnioną innym kolorem podstawą .
Punkt drugi. W trójkącie równoramiennym kąty przy podstawie są równe. Dodana jest grafika trójkąta z zaznaczonymi przy podstawie równymi kątami. Zapisana jest równość .
Punkt trzeci. Kąt jest połową kąta . Kąt to połowa kąta . Połowy kątów równych są równe. Dodana jest grafika trójkąta z zaznaczonymi przy podstawie kątami. Zapisana jest równość .
Punkt czwarty: Z trzeciej cechy przystawania trójkątów wiemy, że dwa trójkąt są przystające, jeżeli mają jeden bok równy i dwa kąty przy tym boku równe.
Trójkąty i spełniają ten warunek, więc są przystające. Dodana jest grafika trójkąta z zaznaczonymi przy podstawie kątami. Dodatkowo w trójkącie wyróżnione są trójkąty i . Zapisana jest tożsamość .
Slajd czwarty:
Lektor mówi: Trójkąty przystające mają odpowiadające sobie boki równe. Zatem długości i dwusiecznych kątów przy podstawie trójkąta są równe, co należało udowodnić.
Na grafice z poprzedniego slajdu pojawia się równość .
Slajd piąty:
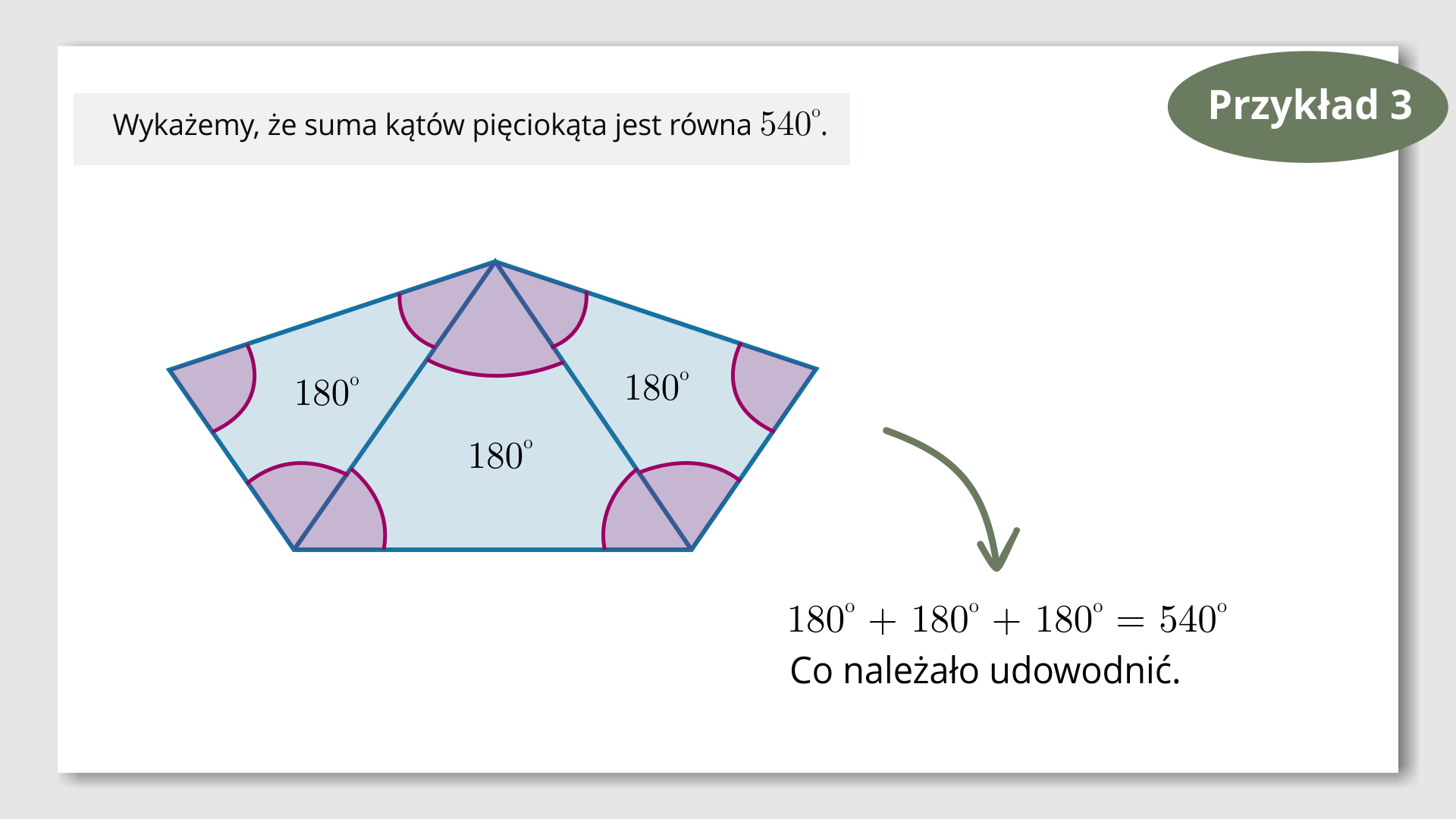
Lektor mówi: Przykład trzeci. Pokażemy teraz, jak znaleźć sumę kątów pięciokąta, korzystając z własności kątów trójkąta. Wykonujemy rysunek pomocniczy. Rysujemy dowolny pięciokąt.
Na grafice interaktywnej dodana jest treść zadania: Wykażemy, że suma kątów pięciokąta jest równa oraz narysowany dowolny pięciokąt. Na grafice są dodane dwa punkty interaktywne, w których są ukryte treści.
Punkt pierwszy. Dzielimy pięciokąt na trzy trójkąty. Dodana jest grafika pięciokąta, gdzie z jednego wierzchołka rozchodzą się dwa odcinki, dzieląc tą figurę na trzy trójkąty.
Punkt drugi. Suma kątów w każdym z trójkątów jest równa . Dodana jest grafika pięciokąta podzielonego na trzy trójkąty. Zaznaczone jest, że suma kątów każdego z tych trójkątów jest równa .
Slajd szósty:
Lektor mówi: Suma kątów pięciokąta jest równa sumie kątów tych trójkątów.
Na grafice z poprzedniego slajdu pojawia się działanie: .
Slajd siódmy:
Lektor mówi: Przykład czwarty. Udowodnimy teraz przydatną własność rombu, korzystając z własności trójkąta równobocznego. Spróbuj udowodnić tę własność, korzystając z własności kątów trójkąta prostokątnego.
Na filmie dodana jest treść zadania: W rombie jedna z przekątnych jest równa bokowi. Wykażemy, że kąt rozwarty tego rombu jest dwa razy większy od kąta ostrego.
Lektor mówi: Wykonujemy rysunek pomocniczy. W rombie wszystkie boki są równe. Oznaczmy przez a długość jednego boku. A wierzchołki rombu przez , , , . Zaznaczmy przekątną, która jest równa długości boku rombu.
Na filmie pojawia się romb z zaznaczoną przekątną . Boki , , są oznaczone małą literą .
Lektor mówi: Przekątna podzieliła romb na dwa trójkąty równoboczne. Każdy kąt trójkąta równobocznego ma miarę .
W filmie na rysunku przedstawiającym romb pojawiają się zaznaczone kąty , ,, , oraz , każdy z nich ma miarę .
Lektor mówi: Zatem kąt ostry rombu ma miarę , a kąt rozwarty . Wynika z tego, że kąt rozwarty jest dwa razy większy od kąta ostrego, co należało udowodnić.
Na filmie pojawiają się trzy równości. Pierwsza . Druga . Trzecia .
Slajd ósmy:
Lektor mówi: Przykład piąty. Nim rozwiążemy następne zadanie, przypomnijmy, że sześcian to prostopadłościan, w którym wszystkie krawędzie są równe. Długości krawędzi czerwonych sześcianów są podane, więc możemy obliczyć ich objętości.
Na grafice interaktywnej jest zapisana treść zadania: Dane są czerwone sześciany o krawędziach równych odpowiednio , , . Wykażemy, że długość krawędzi zielonego sześcianu, którego objętość jest równa sumie objętości czerwonych sześcianów jest o większa od średniej arytmetycznej długości krawędzi czerwonych sześcianów. Pod treścią zadania są narysowane cztery sześciany. Trzy czerwone i jeden zielony. Każdy z nich ma inną długość krawędzi. Czerwone sześciany mają długości krawędzi , , . Zielony sześcian ma krawędzie długości . Pod każdym sześcianem jest punkt interaktywny, w którym są ukryte treści.
Pod sześcianem o krawędzi długości jest punkt interaktywny skrywający treść:
objętość sześcianu o krawędzi długości .
Pod sześcianem o krawędzi długości jest punkt interaktywny skrywający treść:
objętość sześcianu o krawędzi długości .
Pod sześcianem o krawędzi długości jest punkt interaktywny skrywający treść:
objętość sześcianu o krawędzi długości .
Slajd dziewiąty:
Lektor mówi: Obliczamy sumę objętości czerwonych sześcianów i długość krawędzi zielonego sześcianu. Wyznaczymy średnią arytmetyczną długości krawędzi czerwonych sześcianów i porównamy z długością krawędzi zielonego sześcianu.
Na grafice znikają sześciany, a pojawiają się następujące obliczenia: , , , , , .
Lektor mówi: Krawędź ta jest o większa od obliczonej średniej, co należało udowodnić.
Na ekranie pojawia się równość: .
Slajd dziesiąty:
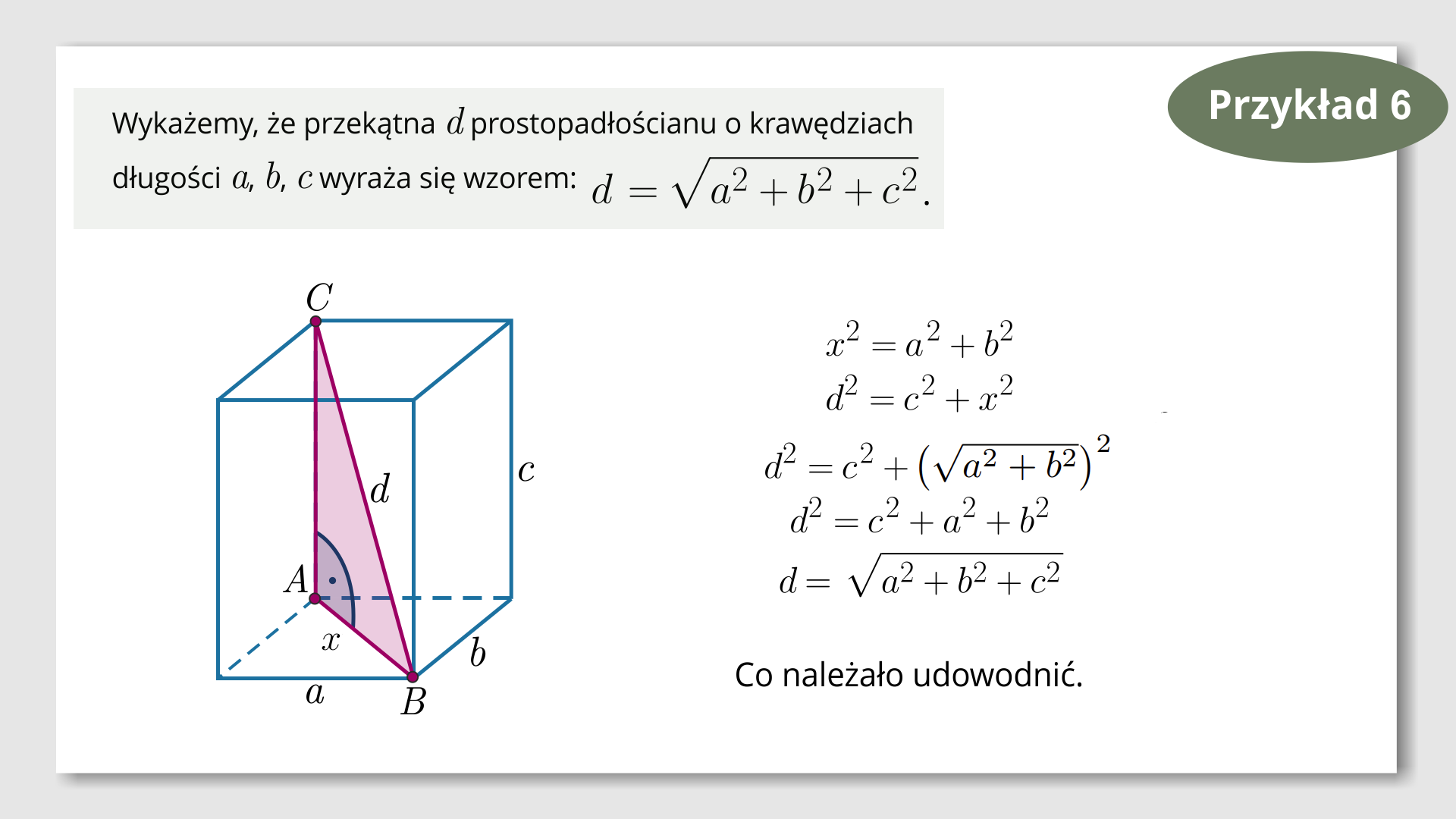
Lektor mówi: Przykład szósty. Obliczymy długość przekątnej, korzystając z twierdzenia Pitagorasa. W tym celu rozważmy trójkąt prostokątny , którego jedna przyprostokątna to przekątna podstawy, a druga to wysokość prostopadłościanu. Wykonujemy rysunek pomocniczy.
Na grafice interaktywnej pojawia się treść zadania: Wykażemy, że przekątna prostopadłościanu o krawędziach długości , , wyraża się wzorem . Pod treścią zadania są narysowane dwa identyczne prostopadłościany o długościach podstawy oraz i wysokości . W pierwszym prostopadłościanie jest zaznaczona przekątna . W drugim prostopadłościanie jest zaznaczony trójkąt prostokątny, którego przeciwprostokątna jest przekątną o końcach w wierzchołkach oraz . Kąt prosty znajduje się w wierzchołku dolnej podstawy. Na grafice znajduje się punkt interaktywny skrywający treść: Nim rozwiążemy zadanie, przypomnijmy, że w prostopadłościanie wszystkie ściany są prostokątami. Przekątna prostopadłościanu to odcinek łączący dwa wierzchołki nie leżące przy jednej ścianie.
Slajd jedenasty:
Lektor mówi: Obliczamy najpierw długość przekątnej podstawy - korzystamy z twierdzenia Pitagorasa. Teraz obliczamy długość przekątnej prostopadłościanu. Korzystamy z twierdzenia Pitagorasa dla trójkąta , w którym przeciwprostokątna jest przekątną prostopadłościanu. Otrzymujemy, że przekątna prostopadłościanu jest równa pierwiastkowi sumy kwadratów długości krawędzi prostopadłościanu, co należało udowodnić.
Na grafice pojawiają się obliczenia: , , , , . Co należało udowodnić.
Wykaż, że suma kątów ośmiokąta jest równa .
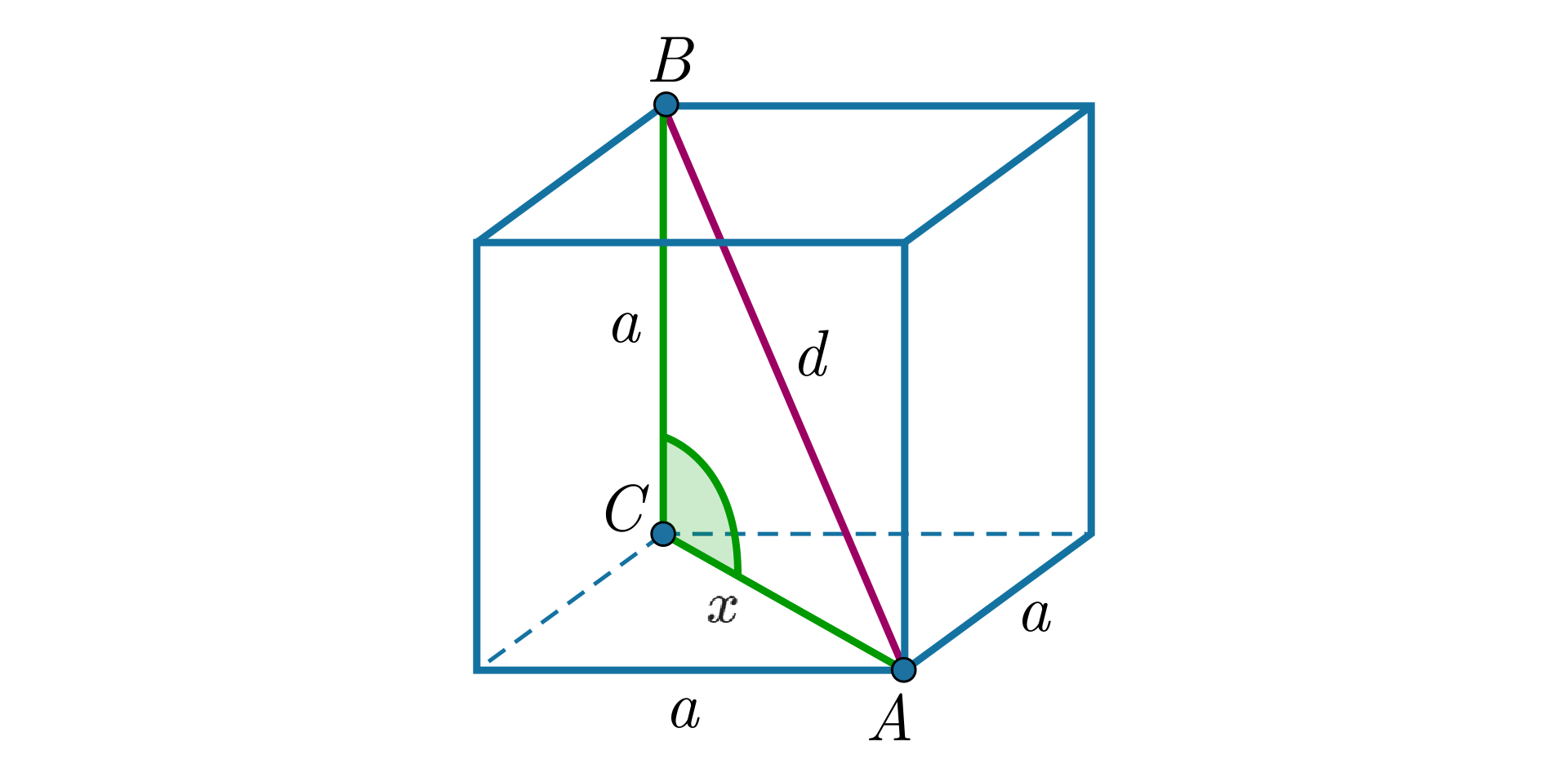
Wykaż, że przekątna sześcianu o krawędzi długości wyraża się wzorem .
Zestaw ćwiczeń interaktywnych
Wykaż, że w siedmiokącie liczba przekątnych jest dwa razy większa od liczby boków.
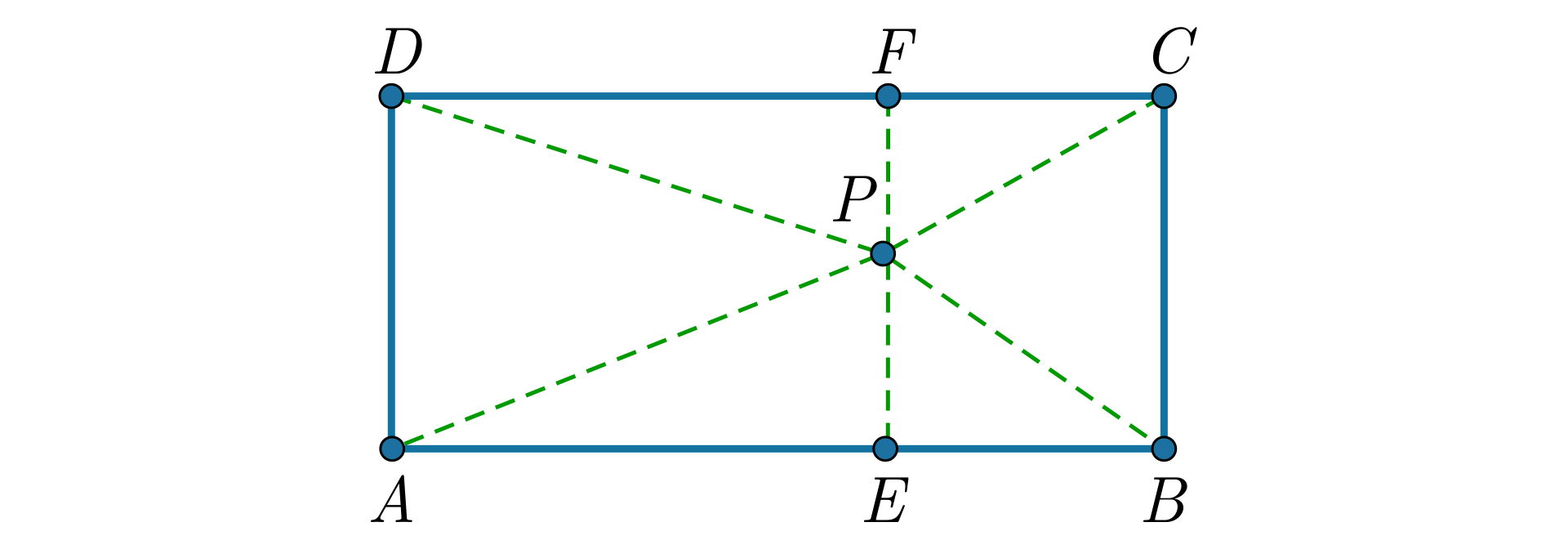
Wewnątrz prostokąta obrano punkt . Wykaż, że .
Słownik
część twierdzenia, która opisuje warunki, przy których spełnione jest twierdzenie.
część twierdzenia zawierająca własność, która zachodzi, gdy spełnione są warunki opisane w założeniu.
prawdziwość tezy jest dowodzona bezpośrednio z założeń twierdzenia, wcześniej udowodnionych twierdzeń, ustalonych reguł postępowania.
Notatnik
Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.