8. Szczególne trójkąty prostokątne

RSqdCaxK9BJGC

W materiale omówimy własności dwóch rodzajów trójkątów. Skupimy uwagę na trójkątach prostokątnych, które mają kąty ostre o miarach $30 °$ i $60 °$ lub oba kąty ostre mają miary $45 °$ . Takie trójkąty są często określane mianem trójkątów charakterystycznych. Znajomość zależności, które występują pomiędzy długościami ich boków pozwala na rozwiązanie wielu problemów geometrycznych.

Trójkąt prostokątny równoramienny

R9FtK2hFRw4T01

Rysunek dwóch trójkątów prostokątnych równoramiennych o kątach 90 stopni, 45 stopni i 45 stopni. Pierwszy trójkąt ma przyprostokątne równe a i przeciwprostokątną równą a pierwiastek z dwóch. Pod trójkątem znajdują się zapisy: a - długość przyprostokątnej, a pierwiastków z dwóch - długość przeciwprostokątnej, 45 stopni, 45 stopni, 90 stopni - miary kątów. Drugi trójkąt ma przyprostokątne równe jedna druga razy x razy pierwiastek z dwóch i przeciwprostokątną równą x. Pod trójkątem znajdują się zapisy: jedna druga x pierwiastków z dwóch - długość przyprostokątnej, x - długość przeciwprostokątnej, 45 stopni, 45 stopni, 90 stopni - miary kątów. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Aby podać długości boków w trójkącie prostokątnym równoramiennym, wystarczy znać długość tylko jednego z boków.

RU9wXB2S1MRS31

Rysunki trzech trójkątów prostokątnych równoramiennych. Pierwszy trójkąt ma przyprostokątne równe 4 i przeciwprostokątną cztery pierwiastki z dwóch. Drugi trójkąt ma przyprostokątne równe 1 i przeciwprostokątną pierwiastek z dwóch. Trzeci trójkąt ma przyprostokątne równe pierwiastek z dwóch i przeciwprostokątną równą 2. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Przykład 1

Przeciwprostokątna trójkąta prostokątnego równoramiennego jest równa $6$ . Oblicz obwód $L$ tego trójkąta. Wymierne przybliżenie obwodu podaj z dokładnością do jednego miejsca po przecinku.

RfFMRgW7SWeQg1

Rysunek trójkąta prostokątnego równoramiennego o przyprostokątnych równych a i przeciwprostokątnej równej 6. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

W trójkącie równoramiennym przyprostokątne są równe. Oznaczmy przez $a$ długość przyprostokątnej i zapiszmy równość wynikającą z twierdzenia Pitagorasa.

a^{2} + a^{2} = 6^{2}

2 a^{2} = 36 / : 2

a^{2} = 18

a = \sqrt{18}

Długość przyprostokątnej wyraża się liczbą niewymierną. Możemy w dalszych rozważaniach uwzględniać wartość dokładną: $\sqrt{18}$ lub $3 \sqrt{2}$ (wyłączając czynnik przed znak pierwiastka) lub przybliżoną

\sqrt{18} = 4, 2426 \dots \approx 4, 24

3 \sqrt{2} = 3 \cdot 1, 414 . . . \approx 3 \cdot 1, 41 = 4, 23

Obliczamy obwód trójkąta.

Sposób $I$	Sposób $II$
$L = \sqrt{18} + \sqrt{18} + 6$	$L = 3 \sqrt{2} + 3 \sqrt{2} + 6$
$L = 2 \sqrt{18} + 6$	$L = 6 \sqrt{2} + 6$
$L \approx 2 \cdot 4, 24 + 6$	$L \approx 6 \cdot 1, 41 + 6$
$L \approx 14, 48$	$L \approx 14, 46$

Obwód prostokąta jest równy w przybliżeniu $14, 5$ .

Przykład 2

Obliczymy promień okręgu opisanego na trójkącie prostokątnym równoramiennym $A B C$ , którego pole jest równe $4, 5 {cm}^{2}$ .

R1eDkaWdnuE131

Rysunek okręgu opisanego na trójkącie prostokątnym równoramiennym A B C gdzie AB i BC to przyprostokątne. Przeciwprostokątna AC jest średnicą tego okręgu. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Obliczymy długość przyprostokątnej, korzystając ze wzoru na pole trójkąta.
$P = \frac{1}{2} \cdot |A B| \cdot |B C|$ , gdzie $|A B| = |B C|$

\frac{1}{2} {|A B|}^{2} = 4, 5

{|A B|}^{2} = 9

|A B| = 3

|A B| > 0

Promień okręgu opisanego na trójkącie jest równy połowie długości przeciwprostokątnej.

r = \frac{|A C|}{2}

|A C| = \sqrt{{|A B|}^{2} + {|B C|}^{2}} = \sqrt{9 + 9} = 3 \sqrt{2}

r = \frac{3}{2} \sqrt{2}

r = 1, 5 \sqrt{2} cm

Promień okręgu opisanego na trójkącie $A B C$ jest równy $1, 5 \sqrt{2} cm$ .

Przykład 3

Sześciokąt $A B C D E F$ zbudowany jest z dwóch przystających równoramiennych trójkątów prostokątnych. Przeciwprostokątna w każdym z tych trójkątów ma długość $12$ . Stosunek długości odcinków $E B$ do $F E$ jest równy $2 : 1$ . Obliczymy obwód wielokąta $A B C D E F$ .

RjNM0bA1cfSd91

Rysunek sześciokąta A B C D E F zbudowanego z dwóch przystających trójkątów prostokątnych A B F i E C D przylegających do siebie częścią przeciwprostokątnych. W trójkącie A B F boki AB i AF to przyprostokątne, BF przeciwprostokątna. W trójkącie E C D boki ED i CD to przyprostokątne, EC przeciwprostokątna. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Stosunek długości odcinków $E B$ do $F E$ jest równy $2 : 1$ , zatem

długość odcinka $E B$ stanowi $\frac{2}{3}$ długości odcinka $F B$ ,
długość odcinka $F E$ stanowi $\frac{1}{3}$ długości odcinka $F B$ .

|E B| = \frac{2}{3} \cdot |F B|

|E B| = \frac{2}{3} \cdot 12 = 8

|E F| = \frac{1}{3} \cdot |F B|

|E F| = \frac{1}{3} \cdot 12 = 4

Oznaczmy przez $a$ długość przyprostokątnej trójkąta $A B F$ . Obliczamy $a$ , korzystając z twierdzenia Pitagorasa.

a^{2} + a^{2} = 1 2^{2}

2 a^{2} = 144

a^{2} = 72

a = \sqrt{72}

a = \sqrt{36 \cdot 2} = 6 \sqrt{2}

Obliczamy obwód sześciokąta $A B C D E F$ .

L = |A F| + |F E| + |E D| + |D C| + |B C| + |B A|

L = a + |E F| + a + a + (|E C| - |E B|) + a

L = 4 a + 4 + (12 - 8)

L = 4 \cdot 6 \sqrt{2} + 4 + 4

L = 4 (6 \sqrt{2} + 2)

Obwód sześciokąta jest równy $4 (6 \sqrt{2} + 2)$ .

Trójkąt o kątach 30°, 60°, 90°

Przykład 4

Bok trójkąta równobocznego $A B C$ ma długość $2 a$ . Obliczmy miary kątów i długości boków trójkąta $C D B$ , gdzie punkt $D$ jest spodkiem wysokości poprowadzonej z wierzchołka $C$ .

R19UjYifi7kwP1

Rysunek trójkąta równobocznego A B C o boku długości 2a i wysokości CD = h. Wysokość podzieliła bok AB trójkąta na dwa równe odcinki AD = DB = a. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

W trójkącie równobocznym każdy kąt ma miarę równą $60 °$ . Kąt $A B C$ jest kątem w trójkącie równobocznym, zatem jego miara jest równa $60 °$

|∡ D B C| = 60 °

Wysokość $C D$ jest prostopadła do podstawy $A B$ , zatem kąt $C D B$ jest kątem prostym

|∡ C D B| = 90 °

Wysokość w trójkącie równobocznym jest zarazem dwusieczną kąta, zatem kąt $D C B$ ma miarę $60 ° : 2 = 30 °$

|∡ D C B| = 30 °

Miary kątów w trójkącie $C D B$ są równe $30 °$ , $60 °$ , $90 °$ .

Trójkąt $D B C$ jest trójkątem prostokątnym, w którym przeciwprostokątna ma długość $2 a$ .

Wysokość $C D$ dzieli podstawę $A B$ na dwa przystające odcinki

x = |D B| = \frac{1}{2} |A B| = \frac{1}{2} \cdot 2 a = a

Korzystając z twierdzenia Pitagorasa, obliczamy długość boku $C D$ , czyli wysokość $h$ trójkąta $C D B$

h^{2} + a^{2} = {(2 a)}^{2}

h^{2} = 4 a^{2} - a^{2}

h^{2} = 3 a^{2}

h = a \sqrt{3}

bo $a > 0$ i $h > 0$ .

Boki trójkąta $C D B$ mają długości: $2 a$ , $a$ , $a \sqrt{3}$ .

Wysokość dzieli trójkąt równoboczny na dwa przystające trójkąty prostokątne.

Miary kątów w każdym z tych trójkątów są równe: $30 °$ , $60 °$ , $90 °$ .

Jeśli oznaczymy przez $2 a$ długość przeciwprostokątnej w tak otrzymanym trójkącie prostokątnym, to długości pozostałych boków są równe $a$ i $a \sqrt{3}$ . Przy czym naprzeciw kąta o mierze $30 °$ leży przyprostokątna, której długość jest dwukrotnie mniejsza od długości przeciwprostokątnej.

Ważne!

Trójkąt prostokątny o kątach $30 °$ , $60 °$ , $90 °$ .

RbgyWVMQyISS21

Rysunek trójkąta prostokątnego o miarach kątach 30 stopni, 60 stopni i 90 stopni. Długość przeciwprostokątnej - 2a. Długość przyprostokątnej leżącej naprzeciwko kąta 30 stopni - a. Długość przyprostokątnej leżącej przy kącie 30 stopni- a pierwiastek z trzech. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

$2 a$ – długość przeciwprostokątnej,
$a$ – długość przyprostokątnej leżącej naprzeciw kąta $30 °$ ,
$a \sqrt{3}$ - długość przyprostokątnej leżącej przy kącie $30 °$ .

Przykład 5

Torba wykonana jest z dwóch jednakowych kawałków skóry. Każdy z nich ma kształt trapezu równoramiennego, w którym ramię i krótsza podstawa mają długość $30 cm$ , a kąt rozwarty ma miarę $120 °$ .

Ile ${cm}^{2}$ skóry zużyto na wykonanie tej torebki?

Obliczymy pole powierzchni jednego z kawałków skóry, z którego wykonana jest torebka, czyli pole odpowiedniego trapezu.

R1SP1N9OQ6Lsq1

Rysunek trapezu równoramiennego o wysokości h, podstawie dolnej 30 cm i ramieniu równym 30 cm. Wysokość poprowadzona z wierzchołków dolnej podstawy dzieli górną podstawę na trzy odcinki długości: x, 30 cm, x. Powstał trójkąt o kątach 30 stopni, 60 stopni i 90 stopni. Kąt 60 stopni leży naprzeciwko wysokości h trapezu. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Wysokość poprowadzona z wierzchołka krótszej podstawy podzieliła trapez na czworokąt i trójkąt prostokątny o kątach $30 °$ , $60 °$ , $90 °$ . Przeciwprostokątna w tym trójkącie ma długość $30 cm$ , zatem $x = 15 cm$ (przyprostokątna leżąca naprzeciw kąta o mierze $30 °$ ) i $h = 15 \sqrt{3} cm$ (przyprostokątna leżąca przy kącie o mierze
$30 °$ ).

Zatem wysokość trapezu jest równa $15 \sqrt{3} cm$ , a dłuższa podstawa ma długość

15 cm + 30 cm + 15 cm = 60 cm

Obliczamy pole trapezu.

P = \frac{60 + 30}{2} \cdot 15 \sqrt{3}

P = 675 \sqrt{3}

P \approx 1170 {cm}^{2}

Obliczamy, ile ${cm}^{2}$ skóry zużyto, aby wykonać torebkę.

2 \cdot 1170 = 2340

Na wykonanie torebki zużyto około $2340 {cm}^{2}$ skóry.

Zapamiętaj.

R14y9q7Khi4rH

Ilustracja. Nagłówek: Długości boków w trójkącie prostokątnym o kątach 30, 60 i 90 stopni oraz o bokach 45, 45 i 90 stopni. Rysunek pierwszy przedstawia trójkąt prostokątny o kątach 30, 60 i 90 stopni i o następujących bokach: pionowa przyprostokątna

a \sqrt{3}

, podstawa a i przeciwprostokątna 2a. Kąty wewnętrzne są następujące: między przyprostokątnymi

a \sqrt{3}

oraz a oznaczono kąt prosty, między bokami a i 2a oznaczono kąt 60 stopni oraz między bokami 2a i

a \sqrt{3}

oznaczono kąt 30 stopni. Zagadnienie do rysunku: Jak wyznaczyć długości boków oraz obwód w trójkącie prostokątnym o kątach

30 °

60 °

90 °

oraz jednym podanym boku? Rysunek przedstawia trójkąt prostokątny o przeciwprostokątnej o długości 4. Zaznaczono kąty wewnętrzne trójkąta. Między przyprostokątnymi oznaczono kąt prosty, między podstawą a przeciwprostokątną oznaczono kąt 60 stopni oraz między pionową przyprostokątną a przeciwprostokątną oznaczono kąt 30 stopni. Mamy zależność:

2 a = 4

, zatem

a = 2

oraz

a \sqrt{3} = 2 \sqrt{3}

. Zatem obwód trójkąta wynosi:

L = 6 + 2 \sqrt{3}

, Rysunek drugi przedstawia trójkąt prostokątny o kątach wewnętrznych 45, 45 i 90 stopni. Ilustracja przedstawia równoramienny trójkąt prostokątny o przyprostokątnych a i przeciwprostokątnej

a \sqrt{2}

. W trójkącie zaznaczono trzy kąty wewnętrzne: kąt prosty między przyprostokątnymi oraz dwa kąty o mierze czterdziestu pięciu stopni między przeciwprostokątną a każdą z przyprostokątnych. Zagadnienie dotyczące trójkąta drugiego: Jak wyznaczyć długości boków oraz obwód w trójkącie prostokątnym o kątach

45 °

45 °

90 °

oraz jednym podanym boku? Rysunek przedstawia trójkąt prostokątny, którego podstawa wynosi a oraz przeciwprostokątna wynosi 2. Zaznaczono kąty wewnętrzne trójkąta. Między przyprostokątnymi kąt prosty, między każdą przyprostokątną a przeciwprostokątną zaznaczono kąt 45 stopni. Mamy zależność:

a \sqrt{2} = 2

, zatem

a = \sqrt{2}

.

Długości boków wynoszą

\sqrt{2}

\sqrt{2}

oraz

2

. Zatem obwód jest równy:

L = 2 \sqrt{2} + 2

Ćwiczenie 1

Trójkąty na rysunkach są prostokątne i równoramienne. Wyznacz $x$ na każdym z poniższych rysunków.

R6f5Wru6lenlQ

Trójkąt o podstawie długości 52 i ramionach długości x. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1O4QZmomSqhx

Trójkąt o podstawie długości x i ramionach długości 11. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RYnSLUvD7E8Y0

Trójkąt o przeciwprostokątnej długości 2 i wysokości opuszczonej na ten bok długości x. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Rc7hj9dHVIRTs

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RseMPrPBtG9Hx

Ćwiczenie 2

długość przynajmniej jednego z boków jest wyrażona liczbą niewymierną
przeciwprostokątna jest dwukrotnie dłuższa od przyprostokątnej
stosunek obwodu do długości przeciwprostokątnej jest równy $\sqrt{2}$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 3

R1Ts8nzEUH91U

Kąty trójkąta są równe

45 °

45 °

90 °

. Najdłuższy bok ma długość

m

. Oblicz sumę długości krótszych boków. Uzupełnij odpowiedź, przeciągając w luki odpowiednie liczby w odpowiedniej kolejności.

\frac{m}{\sqrt{2}} +

\frac{m \sqrt{2}}{2}

, 2.

\frac{m}{\sqrt{2}}

, 3.

\frac{2m}{\sqrt{2}}

, 4.

\frac{3 m \sqrt{2}}{2}

, 5.

\frac{2 m \sqrt{2}}{2}

, 6.

\frac{m \sqrt{2}}{m}

, 7.

m \sqrt{2}

=

\frac{m \sqrt{2}}{2}

, 2.

\frac{m}{\sqrt{2}}

, 3.

\frac{2m}{\sqrt{2}}

, 4.

\frac{3 m \sqrt{2}}{2}

, 5.

\frac{2 m \sqrt{2}}{2}

, 6.

\frac{m \sqrt{2}}{m}

, 7.

m \sqrt{2}

=

\frac{m \sqrt{2}}{2}

, 2.

\frac{m}{\sqrt{2}}

, 3.

\frac{2m}{\sqrt{2}}

, 4.

\frac{3 m \sqrt{2}}{2}

, 5.

\frac{2 m \sqrt{2}}{2}

, 6.

\frac{m \sqrt{2}}{m}

, 7.

m \sqrt{2}

=

\frac{m \sqrt{2}}{2}

, 2.

\frac{m}{\sqrt{2}}

, 3.

\frac{2m}{\sqrt{2}}

, 4.

\frac{3 m \sqrt{2}}{2}

, 5.

\frac{2 m \sqrt{2}}{2}

, 6.

\frac{m \sqrt{2}}{m}

, 7.

m \sqrt{2}

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 4

RnxImFeaKGWqK

Dany jest trójkąt prostokątny równoramienny. Oblicz obwód

L

tego trójkąta w podanych przypadkach. Uzupełnij zdania, przeciągając w luki odpowiednie liczby. Kiedy przyprostokątna tego trójkąta ma długość

2

, wtedy obwód tego trójkąta wynosi

4

+

4 \sqrt{2}

, 2.

12

, 3.

3 \sqrt{2}

, 4.

2 \sqrt{2}

, 5.

2

, 6.

6

, 7.

2 \sqrt{2}

, 8.

5 \sqrt{2}

. Kiedy przeciwprostokątna tego trójkąta ma długość

\sqrt{72}

, wtedy obwód tego trójkąta wynosi

4

+

4 \sqrt{2}

, 2.

12

, 3.

3 \sqrt{2}

, 4.

2 \sqrt{2}

, 5.

2

, 6.

6

, 7.

2 \sqrt{2}

, 8.

5 \sqrt{2}

. Kiedy pole tego trójkąta jest równe

8

, wtedy obwód tego trójkąta wynosi

8

+

4 \sqrt{2}

, 2.

12

, 3.

3 \sqrt{2}

, 4.

2 \sqrt{2}

, 5.

2

, 6.

6

, 7.

2 \sqrt{2}

, 8.

5 \sqrt{2}

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 5

R15ayuthv6tRy

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 6

Czy w poniższym trójkącie $A B C$ bok $B C$ jest najdłuższy?

R1JVheq5mm0iI1

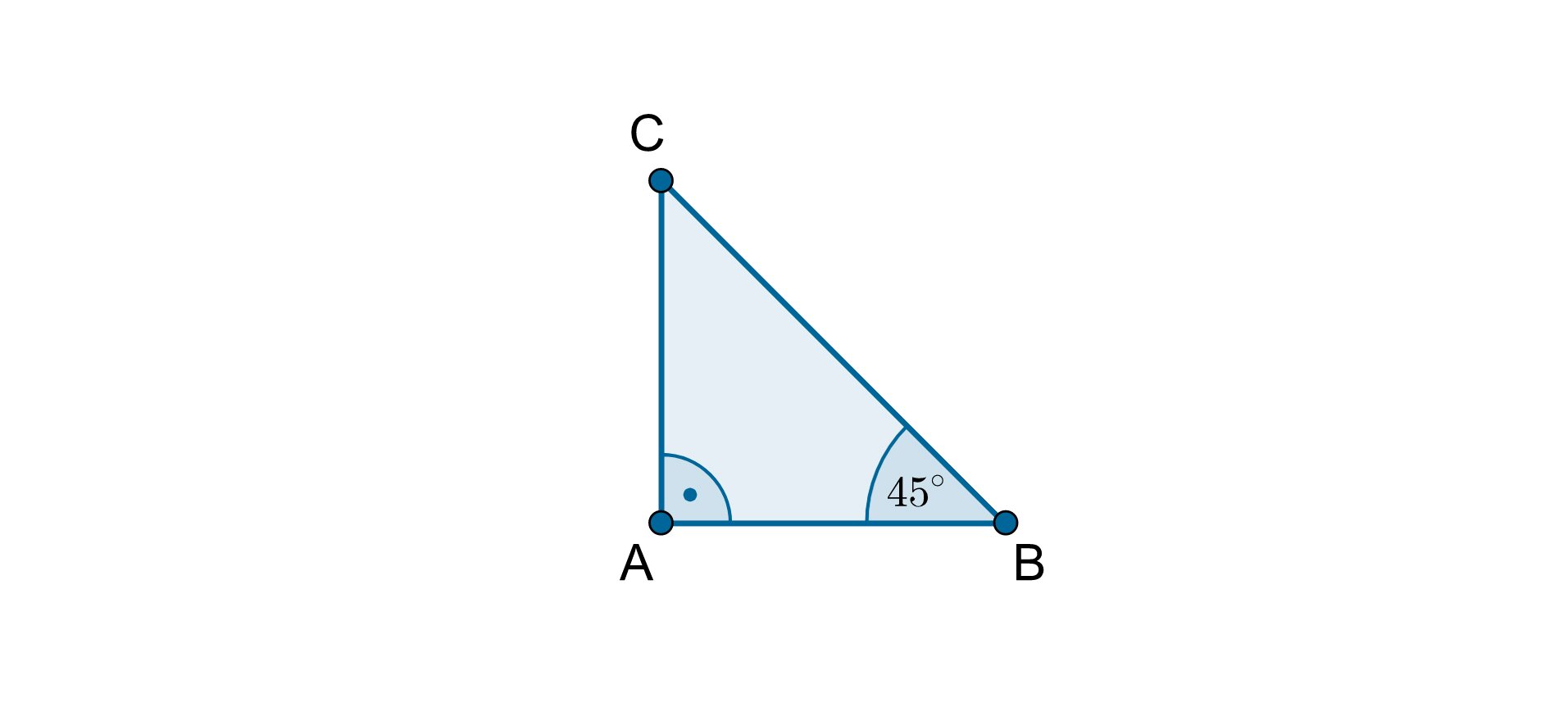
Ilustracja przedstawia trójkąt prostokątny A B C, w którym kąt prosty znajduje się przy wierzchołku A. Boki A B i A C są przyprostokątnymi, a bok B C jest przeciwprostokątną tego trójkąta. Kąt A B C ma miarę 45 stopni. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Rx54icBucecfO

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 7

RrpQjDr45E75l

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Zauważ, że kąt ostry w tym równoległoboku ma miarę $45 °$ , więc wysokość opuszczona na dłuższy bok tworzy trójkąt, którego kąty mają miary $90 °$ , $45 °$ i $45 °$ .

Ćwiczenie 8

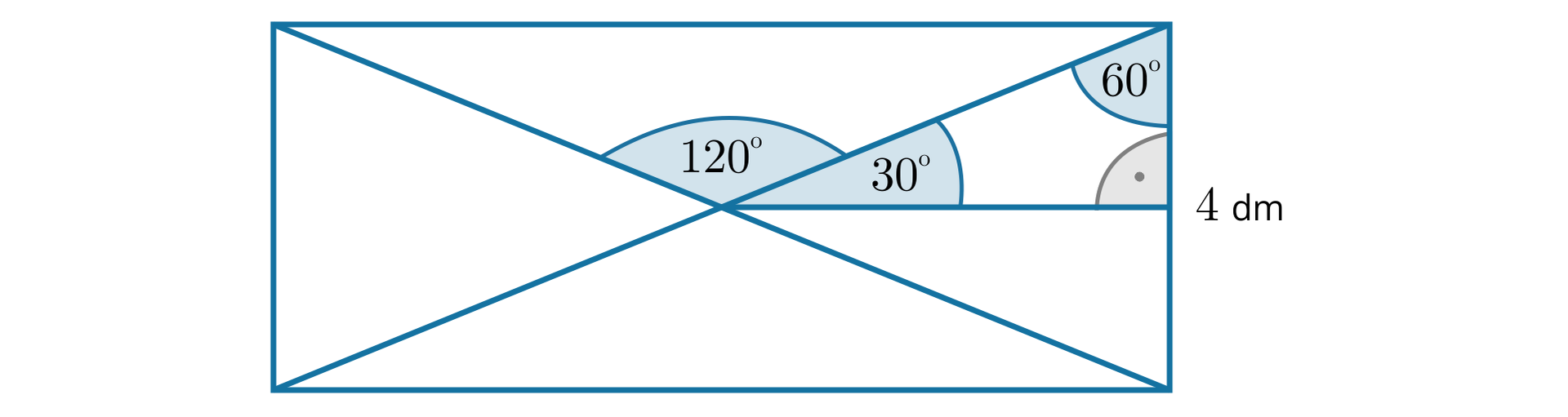
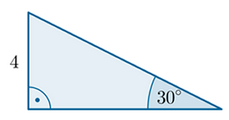
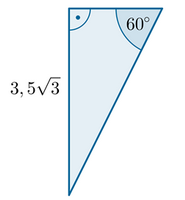
Zapoznaj się z poniższym rysunkiem, na którym znajdują się trzy trójkąty.

R1Xa1S2LN1eyN

Trójkąt prostokątny z kątem o mierze 30°, na przeciw którego znajduje się przyprostokątna o długości 4. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R12S05xqFapif

Trójkąt prostokątny z kątem o mierze 60°, na przeciw którego znajduje się przyprostokątna o długości 3,53. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1Tlk6pdlhCb5

Trójkąt prostokątny z kątem o mierze 30° oraz z przeciwprostokątną długości 10. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RzB1oK4SGycjG

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 9

Zapoznaj się z poniższym rysunkiem trójkąta.

RVYDxGMe1D3QR1

Rysunek trójkąta prostokątnego o przyprostokątnych równych 9 i k oraz przeciwprostokątnej a. Bok k leży naprzeciw kąta 30 stopni. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1FsoTN2lMPLk

$k = 3 \sqrt{3}$
$a = 18$
$a - k = \sqrt{2}$
$k = 3 \sqrt{2}$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 10

RhxOVJiiplB9h

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Zauważ, że kąty ostre w tym trójkącie mają miary $30 °$ i $60 °$ .

Ćwiczenie 11

Zapoznaj się z poniższym rysunkiem trójkąta.

R1IoqMD8YRvQ41

Rysunek trójkąta prostokątnego o przyprostokątnych y oraz dwa pierwiastki z trzech. Wysokość x opuszczona na przeciwprostokątną trójkąta. Kąt zewnętrzny przy przyprostokątnej y jest równy 120 stopni. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R17kI4VXkSk4l

$x + y = 2 \sqrt{3}$
$x + y = \frac{\sqrt{3}}{2}$
$x + y = 4 \sqrt{3}$
$x + y = 2 + \sqrt{3}$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 12

Punkty: $E$ , $F$ , $G$ są środkami boków trójkąta równobocznego $A B C$ . Punkt $D$ jest punktem przecięcia środkowych boków tego trójkąta i $|D E| = 2$ .

R1cWUK76EK2N11

Rysunek przedstawia trójkąt równoboczny A B C. Zaznaczono punkty E, F i G, które są środkami boków trójkąta. Odcinki A E, B F i C G są jednocześnie wysokościami trójkąta, środkowymi boków oraz dwusiecznymi kątów tego trójkąta. Punktem D oznaczono przecięcie boków A E, B F i C G tego trójkąta. Długość odcinka DE =2. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RWiGXcGOljt20

Połącz w pary wielokąty z odpowiadającymi im obwodami. trójkąt

E D B

Możliwe odpowiedzi: 1.

L = 3 \cdot 4 \sqrt{3} = 12 \sqrt{3}

, 2.

L = 6 + 4 \sqrt{3} + 2 \sqrt{3} = 6 + 6 \sqrt{3}

, 3.

L = 2 + 4 + 2 \sqrt{3} = 6 + 2 \sqrt{3}

, 4.

L = 2 + 2 + 2 \sqrt[]{3} + 2 \sqrt{3} = 4 + 4 \sqrt{3}

trójkąt

E A B

Możliwe odpowiedzi: 1.

L = 3 \cdot 4 \sqrt{3} = 12 \sqrt{3}

, 2.

L = 6 + 4 \sqrt{3} + 2 \sqrt{3} = 6 + 6 \sqrt{3}

, 3.

L = 2 + 4 + 2 \sqrt{3} = 6 + 2 \sqrt{3}

, 4.

L = 2 + 2 + 2 \sqrt[]{3} + 2 \sqrt{3} = 4 + 4 \sqrt{3}

trójkąt

A B C

Możliwe odpowiedzi: 1.

L = 3 \cdot 4 \sqrt{3} = 12 \sqrt{3}

, 2.

L = 6 + 4 \sqrt{3} + 2 \sqrt{3} = 6 + 6 \sqrt{3}

, 3.

L = 2 + 4 + 2 \sqrt{3} = 6 + 2 \sqrt{3}

, 4.

L = 2 + 2 + 2 \sqrt[]{3} + 2 \sqrt{3} = 4 + 4 \sqrt{3}

czworokąt

F D E C

Możliwe odpowiedzi: 1.

L = 3 \cdot 4 \sqrt{3} = 12 \sqrt{3}

, 2.

L = 6 + 4 \sqrt{3} + 2 \sqrt{3} = 6 + 6 \sqrt{3}

, 3.

L = 2 + 4 + 2 \sqrt{3} = 6 + 2 \sqrt{3}

, 4.

L = 2 + 2 + 2 \sqrt[]{3} + 2 \sqrt{3} = 4 + 4 \sqrt{3}

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 13

Rs2ygpC9jqCKU

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 14

RnaasMGOBCb1t

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Notatnik

Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.

R1b8OvSPUG8s3

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

7. Twierdzenie Pitagorasa

9. Dowody geometryczne