Własności figur geometrycznych na płaszczyźnie
7. Twierdzenie Pitagorasa
W Starożytnym Egipcie, ale też w Chinach, Babilonie i Mezopotamii wykorzystywano, tak zwany trójkąt egipski (trójkąt o proporcji boków ) do wyznaczania kąta prostego za pomocą sznurka lub liny, podzielonej na części. Prawdopodobnie Pitagoras odkrył tę zależność obserwując konstrukcje piramid zbudowanych na trójkącie egipskim, na przykład piramidy Chefrena w Egipcie.

Jednym z ważniejszych twierdzeń w matematyce jest twierdzenie zwane dzisiaj twierdzeniem Pitagorasa. Twierdzenie to prawdopodobnie znali już starożytni Egipcjanie, Chińczycy i Hindusi. Starożytni Grecy jego odkrycie i dowód przypisywali greckiemu matematykowi Pitagorasowi.
Pitagoras to grecki filozof i matematyk, urodzony około r. p.n.e. Założył szkołę filozoficzną, która przekształciła się w związek pitagorejski. Pitagoras i jego uczniowie zajmowali się wieloma dziedzinami wiedzy. Dokonali też wielu odkryć matematycznych, np. udowodnili, że suma kątów w trójkącie jest równa kątowi półpełnemu. Jako pierwsi wyodrębnili liczby parzyste i nieparzyste, odkryli liczby niewymierne, wprowadzili pojęcie podobieństwa figur. Sformułowali zasady budowy wielościanów foremnych.
Uruchom aplet i wykonaj zawarte w nim polecenia.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DHN0O84Hn
Twierdzenie to można sformułować też inaczej, wykorzystując zależność między długościami boków trójkąta prostokątnego.
Jeżeli i są długościami przyprostokątnych, zaś długością przeciwprostokątnej w trójkącie prostokątnym, to zachodzi związek

O dowodach twierdzenia Pitagorasa
Znanych jest wiele dowodów twierdzenia Pitagorasa, zarówno geometrycznych, jak i algebraicznych. Oryginalne dowody tego twierdzenia podało wiele znanych postaci historycznych, niezwiązanych bezpośrednio z matematyką, np. jeden z prezydentów Stanów Zjednoczonych James Garfield (Dżejms Garfild), włoski artysta Leonardo da Vinci (Leonardo da Vinci), francuski pisarz Ernest Renan (Ernest Reną).
Uruchom aplet i wykonaj zawarte w nim polecenia.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DHN0O84Hn
Zapoznaj się z poniższym apletem, w którym pokazany jest kolejny przykład dowodu twierdzenia Pitagorasa.
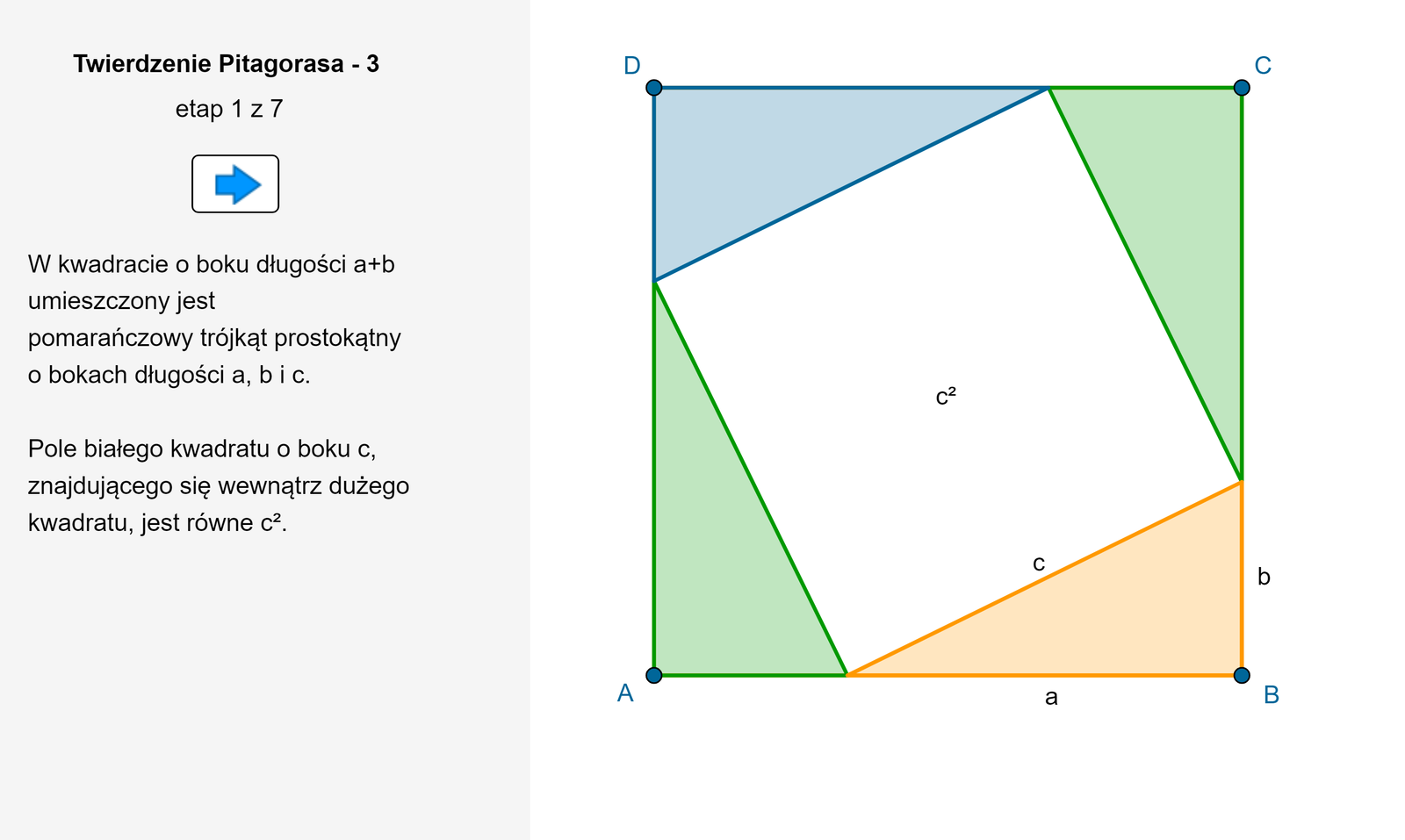
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DHN0O84Hn
Zapoznaj się z apletem przedstawiającym jeszcze jeden dowód twierdzenia Pitagorasa.
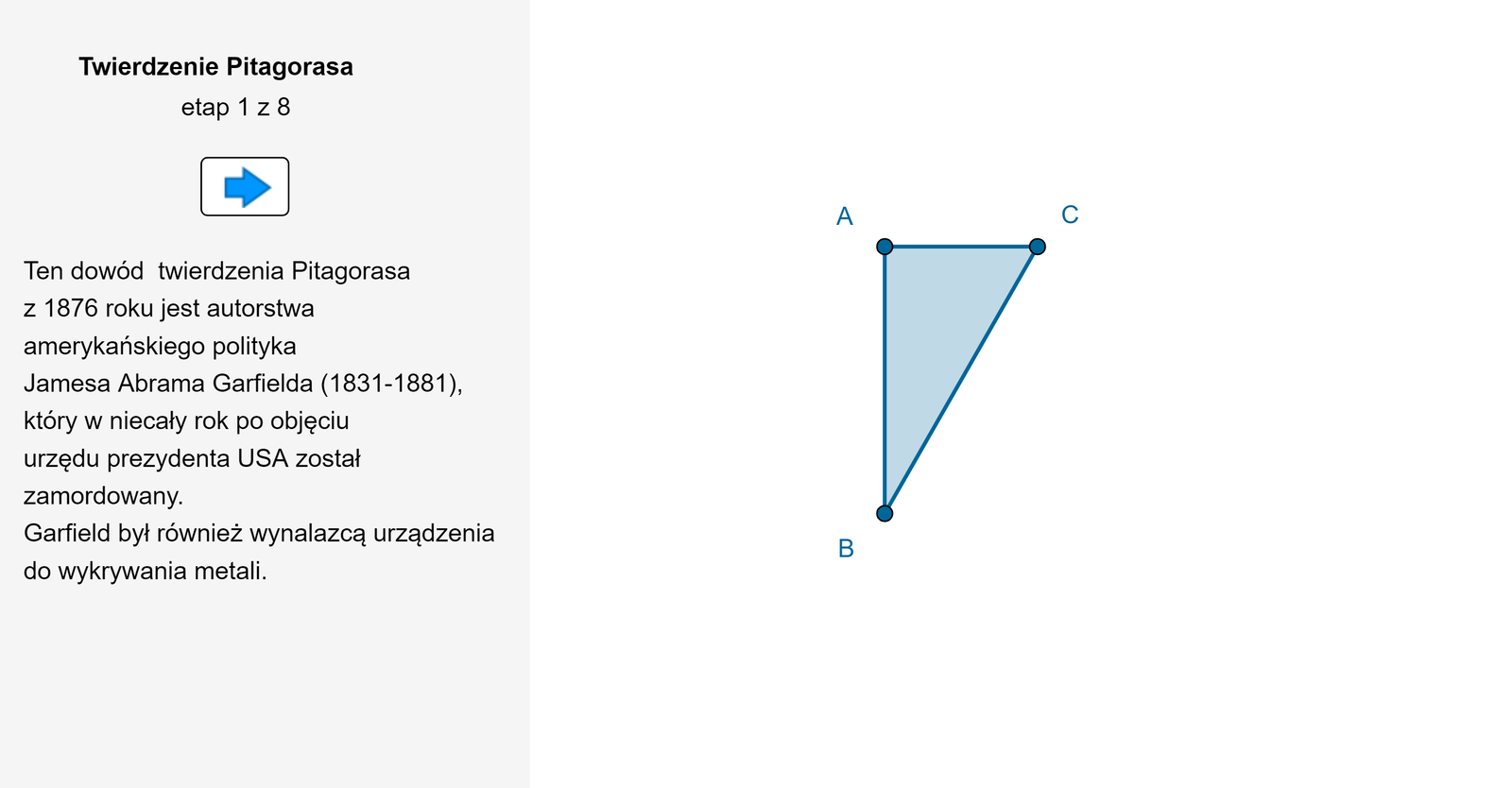
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DHN0O84Hn
Sprawdź, czy dla trójkąta ostrokątnego zachodzi teza twierdzenia Pitagorasa. Sformułuj wniosek.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DHN0O84Hn
Elementy kwadratów zbudowanych na dwóch bokach trójkąta ostrokątnego nie mieszczą się w kwadracie zbudowanym na najdłuższym boku, więc nie zachodzi teza twierdzenia Pitagorasa.
Można udowodnić, że suma kwadratów długości dwóch boków trójkąta jest równa kwadratowi długości najdłuższego boku tylko w przypadku trójkątów prostokątnych. Dla trójkątów ostrokątnych oraz trójkątów rozwartokątnych równość ta nie zachodzi.
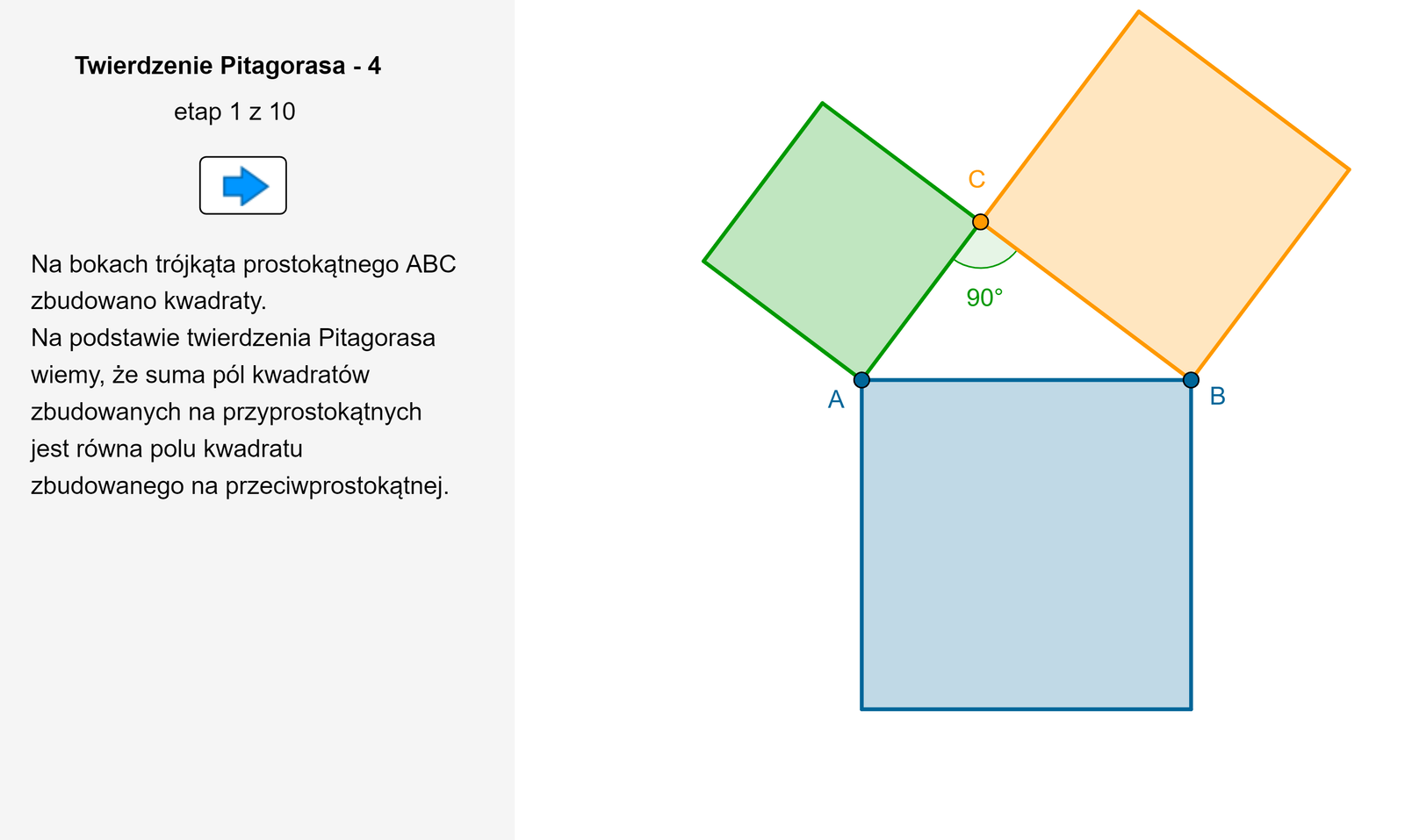
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DHN0O84Hn
Jeżeli na bokach trójkąta prostokątnego zbudujemy dowolne wielokąty podobne (czyli takie, że jeden z nich jest obrazem drugiego w pewnej skali), to suma pól tych wielokątów, które są zbudowane na przyprostokątnych, jest równa polu tego wielokąta, który jest zbudowany na przeciwprostokątnej.
Zmieniaj odpowiednio kształt i wielkość wielokątów zbudowanych na bokach trójkąta prostokątnego. Sprawdź, czy dla pól tych wielokątów spełniony jest związek między polami wielokątów, wynikający z twierdzenia Pitagorasa.
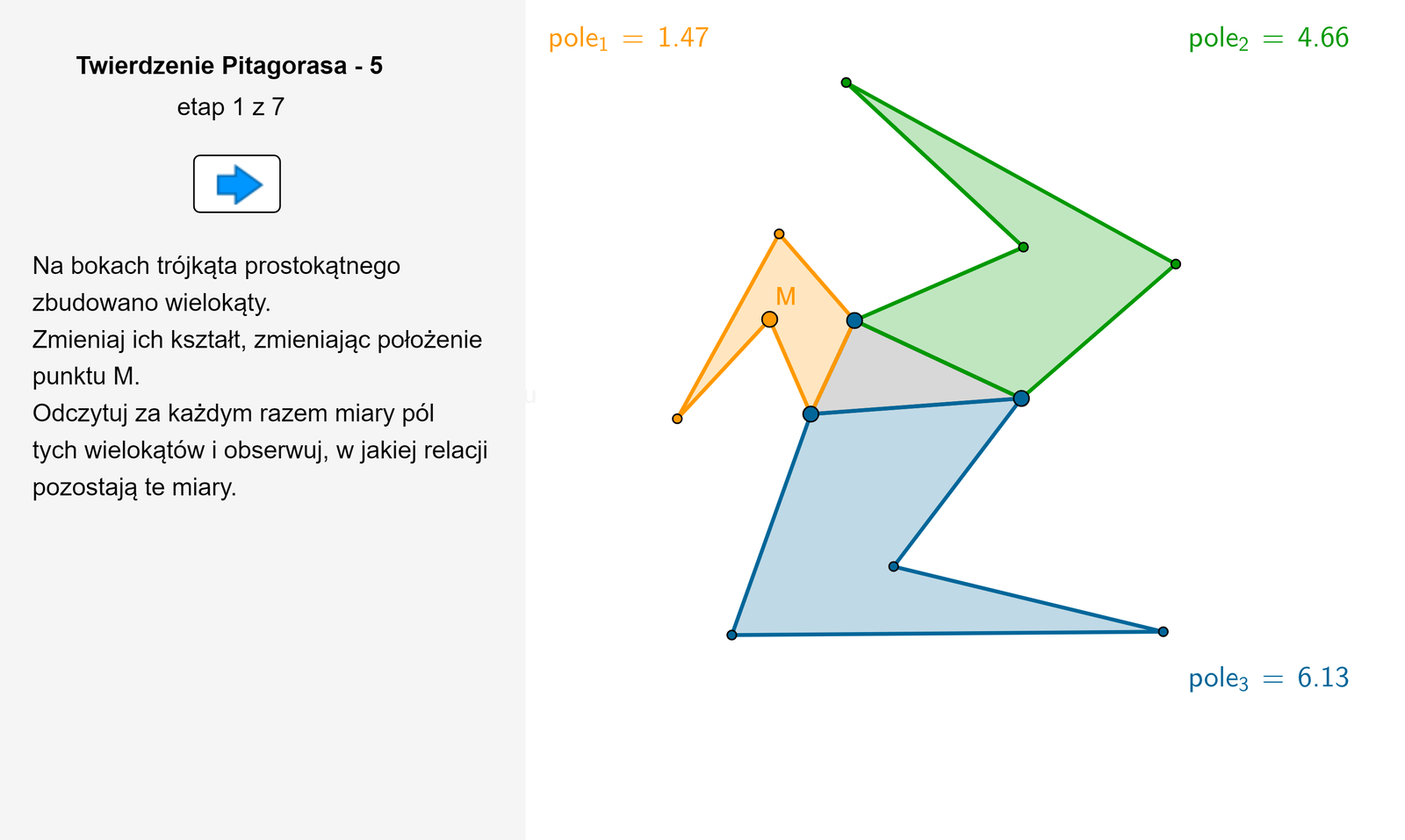
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DHN0O84Hn
Korzystając z twierdzenia Pitagorasa, można obliczyć długość jednego z boków trójkąta prostokątnego, mając dane długości dwóch pozostałych boków.
W trójkącie prostokątnym długości przyprostokątnych są równe i . Znajdźmy długość przeciwprostokątnej tego trójkąta.

Zapisujemy równość wynikającą z twierdzenia Pitagorasa, z której wyznaczamy długość przeciwprostokątnej.
Równanie
ma dwa rozwiązania lub . Długość boku trójkąta wyraża się liczbą dodatnią, zatem uwzględniamy tylko rozwiązanie dodatnie
Przeciwprostokątna trójkąta ma długość .
Jedna z przyprostokątnych trójkąta prostokątnego ma długość , a przeciwprostokątna ma długość . Oblicz długość drugiej przyprostokątnej.

Oznaczamy – długość drugiej przyprostokątnej, . Korzystamy z twierdzenia Pitagorasa.
Druga z przyprostokątnych ma długość .
W trójkącie prostokątnym dwa boki mają długości i . Znajdź długość trzeciego boku tego trójkąta.
Oznaczmy – szukaną długość boku trójkąta .
Długość boku znajdziemy, korzystając z twierdzenia Pitagorasa.
Rozpatrzymy dwa przypadki:
przypadek | przypadek |
|---|---|
Bok, którego długości szukamy, jest przyprostokątną trójkąta. | Bok, którego długości szukamy jest przeciwprostokątną trójkąta. |
Długość trzeciego boku trójkąta jest równa lub .
W podanym twierdzeniu wskaż założenie i tezę. Czy twierdzenie jest prawdziwe?
Jeżeli liczba naturalna dodatnia jest wielokrotnością , to jest podzielna przez
.Jeżeli pole kwadratu jest równe , to jego obwód jest równy .
Jeżeli punkt leży w układzie współrzędnych na osi , to jego druga współrzędna jest równa .
Jeżeli wielokąt jest trapezem, to jego przekątne zawsze przecinają się pod kątem prostym.
Sformułuj podane twierdzenie, korzystając ze schematu „jeżeli … to”.
Pole kwadratu o boku długości jest równe .
W trójkącie równobocznym każdy kąt ma miarę .
Liczba naturalna podzielna przez cztery jest liczbą parzystą.
Pole kwadratu zbudowanego na przeciwprostokątnej wynosi , a pole kwadratu zbudowanego na krótszej przyprostokątnej wynosi . Wynika stąd, że obwód tego trójkąta wynosi 1. , 2. , 3. , 4. , 5. , 6. , pole 1. , 2. , 3. , 4. , 5. , 6. .Pola kwadratów zbudowanych na przyprostokątnych wynoszą kolejno oraz . Wynika stąd, że obwód tego trójkąta wynosi 1. , 2. , 3. , 4. , 5. , 6. , pole 1. , 2. , 3. , 4. , 5. , 6. .Pole kwadratu zbudowanego na przeciwprostokątnej wynosi , a pole kwadratu zbudowanego na krótszej przyprostokątnej wynosi . Wynika stąd, że obwód tego trójkąta wynosi 1. , 2. , 3. , 4. , 5. , 6. , pole 1. , 2. , 3. , 4. , 5. , 6. .
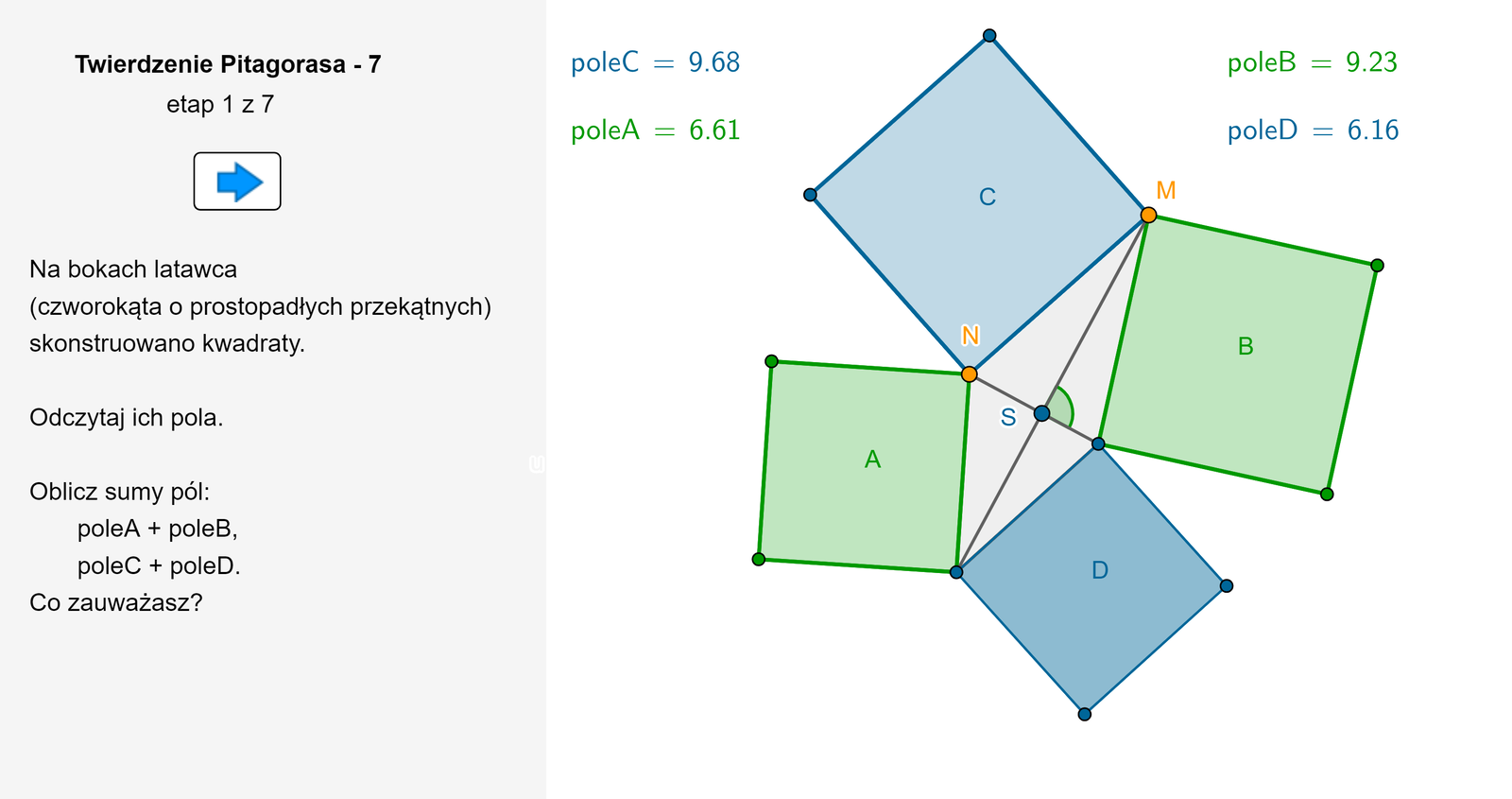
Rysunek przedstawia deltoid (latawiec), czyli czworokąt, którego przekątne są prostopadłe. Na bokach latawca zbudowano kwadraty.
Zmieniaj położenie punktu , również tak, aby uzyskać trójkąt prostokątny. W każdym przypadku porównuj sumy pól kwadratów leżących naprzeciw siebie. Co zauważasz?
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DHN0O84Hn
Dokończ zdanie, wybierając poprawną odpowiedź.
Jeden z boków trójkąta wyraża się liczbą, która nie jest wymierna, gdy: Możliwe odpowiedzi: 1. , , 2. , , 3. , , 4. ,
Losujemy dwie liczby naturalne , ze zbioru liczb naturalnych od do . Liczby
, są długościami przyprostokątnych trójkąta. Znajdź długość przeciwprostokątnej dla trzech przykładowych par wylosowanych liczb.
Notatnik
Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.