Reguła, na podstawie której określa się liczbę wszystkich możliwych wyników doświadczenia losowego, polegającego na wykonaniu po kolei $n$ czynności, z których pierwsza może zakończyć się na jeden z $k_1$ sposobów, druga – na jeden z $k_2$ sposobów, trzecia – na jeden z $k_3$ sposobów i tak dalej do tej czynności, która może zakończyć się na jeden z $k_n$ sposobów. Liczba ta jest równa $k_1·k_2·k_3·\dots ·k_n$.

Obliczymy, ile jest możliwych wyników doświadczenia polegającego na:
a) dwukrotnym rzucie symetryczną, sześcienną kostką do gry,
b) trzykrotnym rzucie symetryczną monetą.
Rozwiązanie:
a) Jeżeli rzucamy jeden raz symetryczną, sześcienną kostką do gry, to możemy otrzymać jeden z sześciu różnych wyników: $1$, $2$, $3$, $4$, $5$, $6$. Wobec tego, liczba wszystkich wyników przy dwukrotnym rzucie symetryczną sześcienną kostką do gry wynosi:
$6·6=36$
b) Jeżeli rzucamy jeden raz symetryczną monetą, to możemy otrzymać jeden z dwóch różnych wyników: orła lub reszkę. Wobec tego, liczba wszystkich wyników przy trzykrotnym rzucie symetryczną monetą wynosi:
$2·2·2=8$

Obliczymy, na ile sposobów można rozmieścić:
a) $8$ kul w $4$ szufladach, przy czym kule i szuflady rozróżniamy,
b) $4$ kule w $8$ szufladach, przy czym kule i szuflady rozróżniamy.
Rozwiązanie:
a) Ponieważ mamy rozmieścić $8$ kul w $4$ szufladach, zatem każda kula może trafić do szuflad na $4$ różne sposoby. Wobec tego, wszystkich możliwości jest:
$4·4·4·4·4·4·4·4=65536$
b) Ponieważ mamy rozmieścić $4$ kule w $8$ szufladach, zatem każda kula może trafić do szuflad na $8$ różnych sposobów. Wobec tego wszystkich możliwości jest:
$8·8·8·8=4096$

Szyfr do sejfu tworzymy z trzech cyfr wybranych spośród następujących: $1$, $2$, $3$, $4$, $5$, $6$, $7$, przy czym cyfry te mogą się powtarzać. Obliczymy, ile jest takich szyfrów.
Rozwiązanie:
Zauważmy, że na każdym z trzech miejsc szyfru możemy wpisać jedną z siedmiu cyfr.
Wobec tego liczba wszystkich możliwych szyfrów jest równa:
$7·7·7=343$

Obliczymy, ile jest:
a) wszystkich liczb czterocyfrowych, w których zapisie nie występuje cyfra zero i cyfry mogą się powtarzać,
b) wszystkich liczb czterocyfrowych o powtarzających się cyfrach, jeśli pierwsza cyfra jest nieparzysta, a pozostałe cyfry są parzyste.
Rozwiązanie:
a) Ponieważ w rozpatrywanych liczbach czterocyfrowych nie występuje cyfra $0$, zatem wszystkich liczb czterocyfrowych, w których cyfry się powtarzają jest:
$9·9·9·9=6561$
b) W rozpatrywanej liczbie pierwsza cyfra musi być nieparzysta, zatem możemy wybrać jedną z $5$ cyfr: $1$, $3$, $5$, $7$, $9$. Następne trzy cyfry muszą być parzyste, więc wybieramy z cyfr: $0$, $2$, $4$, $6$, $8$. Ponieważ cyfry mogą się powtarzać, zatem takich liczb jest:
$5·5·5·5=625$

Obliczymy, na ile sposobów:
a) $5$ osób może wysiąść z windy, która zatrzymuje się na $6$ piętrach,
b) $6$ osób może wysiąść z windy, która zatrzymuje się na $5$ piętrach.
Rozwiązanie:
a) Liczba sposobów, na które $5$ osób może wysiąść z windy, która zatrzymuje się na $6$ piętrach wynosi:
$6·6·6·6·6=7776$
b) Liczba sposobów, na które $6$ osób może wysiąść z windy, która zatrzymuje się na $5$ piętrach wynosi:
$5·5·5·5·5·5=15625$

Z urny, w której znajduje się $11$ kul, w tym $6$ białych i $5$ kul czarnych losujemy dwie kule ze zwracaniem. Wyznaczymy, ile jest możliwości wylosowania kul o różnych kolorach.
Rozwiązanie:
Przedstawmy rozwiązanie zadania za pomocą drzewa. Niech $B$ oznacza kulę białą, a $CZ$ kulę czarną.

R1RvW93m810sx

Z jednego punktu wspólnego poprowadzone są dwie linie w kolorze niebieskim. Nad linią po lewej stronie zapisana jest cyfra 6, nad linią po prawej 5. Na końcu linii z liczbą 6 znajduje się kółko w kolorze białym, z literą B w środku. Na końcu linii z liczbą 5 znajduje się czarne kółko, z oznaczeniem CZ w środku. Po prawej stronie napis: losowanie pierwszej kuli. Od obu kółek poprowadzone są po dwie linie. Nad linią po lewej stronie zapisana jest cyfra 6, nad linią po prawej 5. Na końcu linii z liczbą 6 znajduje się kółko w kolorze białym, z literą B w środku. Na końcu linii z liczbą 5 znajduje się czarne kółko, z oznaczeniem CZ w środku. Po prawej stronie napis: Losowanie drugiej kuli.

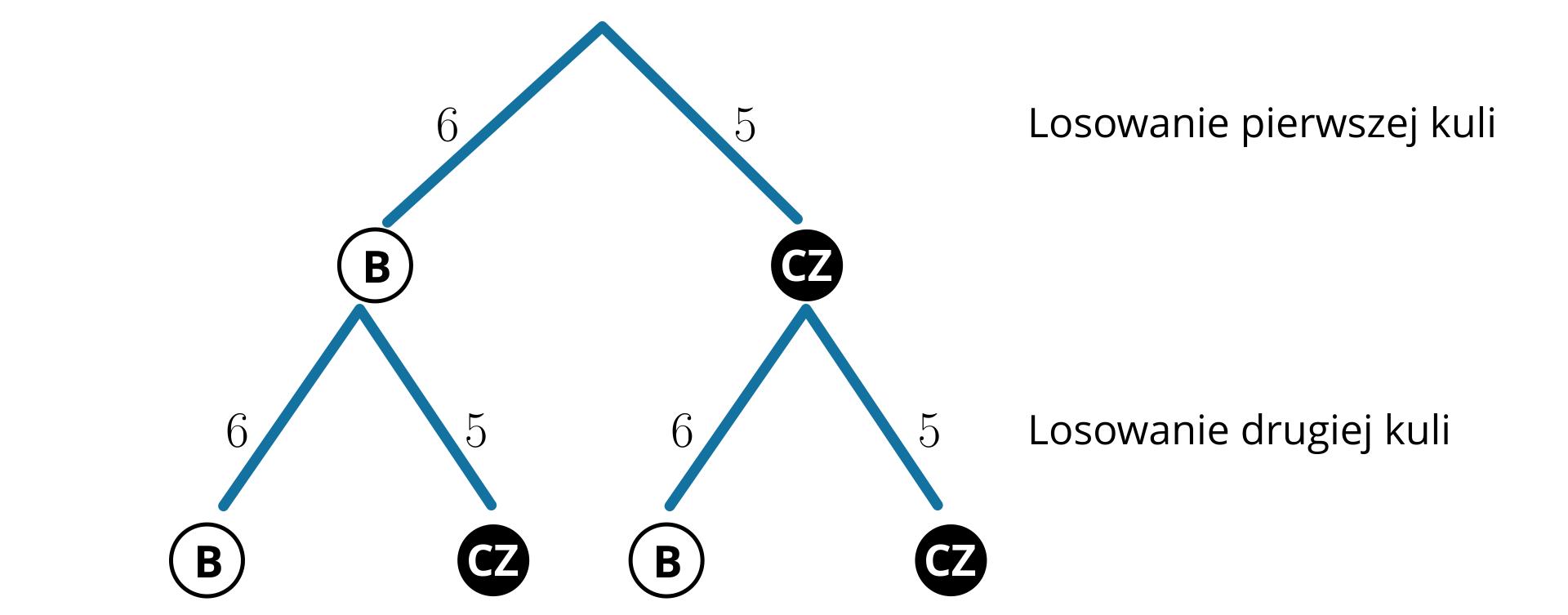
W poniższym schemacie przedstawiono drzewko stochastyczne ilustrujące możliwości wylosowania czarnej i białej kuli w dwóch kolejnych losowaniach ze zwracaniem. Literą B oznaczono sytuację, w której wylosowana kula ma kolor biały, natomiast literami C Z oznaczono sytuację, w której wylosowana kula ma kolor czarny. Lista elementów:

• Nazwa kategorii: START
  Na tym etapie jest 6 kul białych i 5 kul czarnych.
  Elementy należące do kategorii START

  • Nazwa kategorii: B ($\mathrm{I}$ losowanie).
    Na tym etapie jest 6 kul białych i 5 kul czarnych.
    Elementy należące do kategorii B ($\mathrm{I}$ losowanie)

    • Nazwa kategorii: B ($\mathrm{II}$ losowanie).

    • Nazwa kategorii: C Z ($\mathrm{II}$ losowanie).

  • Nazwa kategorii: C Z ($\mathrm{I}$ losowanie).
    Na tym etapie jest 6 kul białych i 5 kul czarnych.
    Elementy należące do kategorii C Z ($\mathrm{I}$ losowanie)

    • Nazwa kategorii: B ($\mathrm{II}$ losowanie). Na tym etapie jest 7 białych kul.

    • Nazwa kategorii: C Z ($\mathrm{II}$ losowanie) Na tym etapie jest 7 czarnych kul.

Ponieważ losujemy dwie kule ze zwracaniem, zatem do rozwiązania zadania bierzemy dwie możliwości:

$\mathrm{I}$. Ze wszystkich kul wylosujemy najpierw kulę białą, wrzucamy ją do puli wszystkich i wybieramy kulę czarną. Takich możliwości jest:
$6·5=30$
$\mathrm{II}$. Ze wszystkich kul wylosujemy najpierw kulę czarną, wrzucamy ją do puli wszystkich i wybieramy kulę białą. Takich możliwości jest:
$5·6=30$
Wobec tego, stosując regułę dodawania, liczba wszystkich możliwych wyników doświadczenia losowego, polegającego na wylosowaniu ze zwracaniem kul o różnych kolorach wynosi:
$6·5+5·6=30+30=60$

Z talii $52$ kart losujemy ze zwracaniem dwie karty. Obliczymy, ile jest możliwych wyników wybrania co najmniej jednego trefla.

Rozwiązanie:
W talii $52$ kart jest $13$ trefli oraz $39$ kart w pozostałych kolorach. Oznaczmy przez $T$ – karty w kolorze trefl, a przez $P$ – karty w pozostałych kolorach. Przedstawmy doświadczenie losowe za pomocą drzewa:

Rtl5IhqNZitrm

Z jednego punktu wspólnego poprowadzone są dwie linie w kolorze niebieskim. Nad linią po lewej stronie zapisana jest liczba 13, nad linią po prawej 39. Na końcu linii z liczbą 13 znajduje się kółko w kolorze różowym, z literą T w środku. Na końcu linii z liczbą 39 znajduje się niebieskie kółko, z literą P w środku. Po lewej stronie napis: I wybór. Od obu kółek poprowadzone są po dwie linie. Nad linią po lewej stronie zapisana jest liczba 13, nad linią po prawej 39. Na końcu linii z liczbą 13 znajduje się kółko w kolorze różowym, z literą T w środku. Na końcu linii z liczbą 39 znajduje się niebieskie kółko, z literą P w środku. Po lewej stronie napis: II wybór.

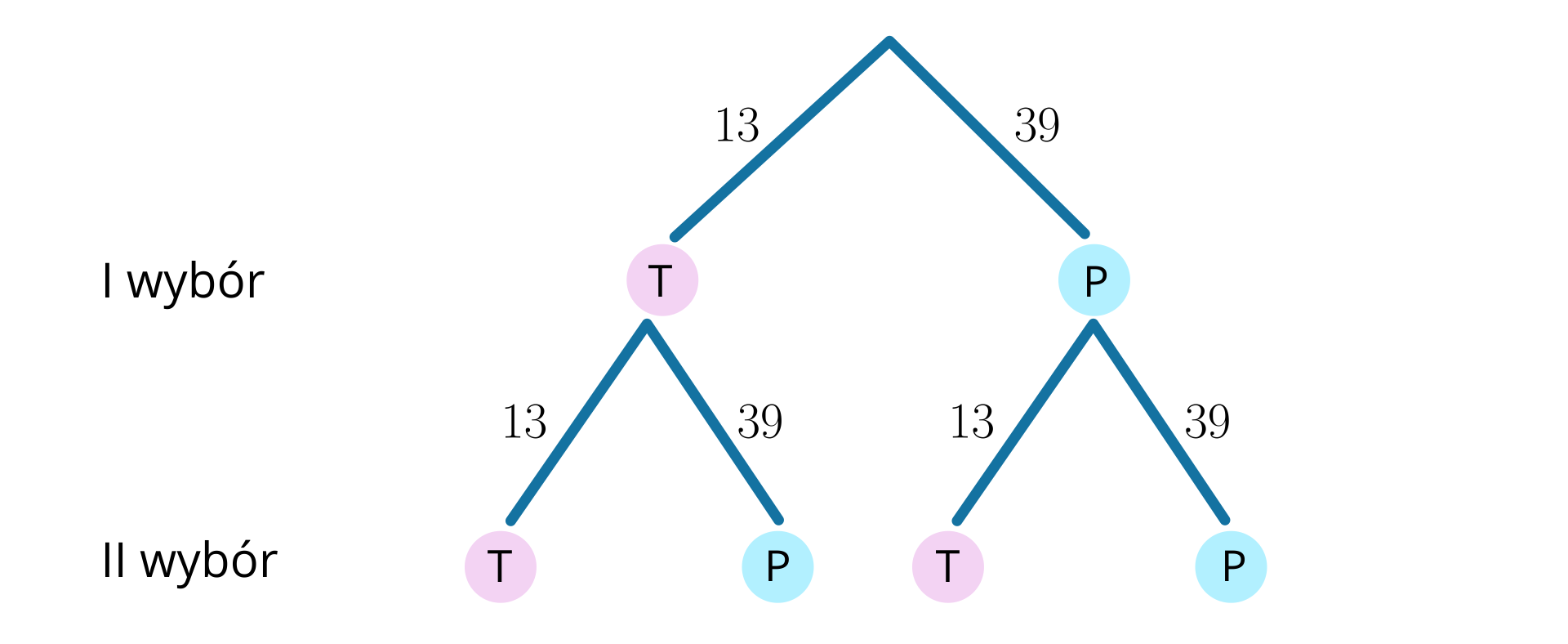
W poniższym schemacie przedstawiono drzewko stochastyczne ilustrujące możliwości wylosowania karty w kolorze trefl i wylosowania karty w innym kolorze w dwóch kolejnych losowaniach bez zwracania. Literą T oznaczono sytuację, w której wylosowana karta jest treflem, natomiast literą P oznaczono sytuację, w której wylosowana karta ma inny kolor. Lista elementów:

• Nazwa kategorii: START
  Na tym etapie mamy 13 trefli i 39 kart pozostałego koloru.
  Elementy należące do kategorii START

  • Nazwa kategorii: T ($\mathrm{I}$ losowanie)
    Na tym etapie mamy 13 trefli i 39 kart pozostałego koloru.
    Elementy należące do kategorii T ($\mathrm{I}$ losowanie)

    • Nazwa kategorii: T ($\mathrm{II}$ losowanie)

    • Nazwa kategorii: P ($\mathrm{II}$ losowanie)

  • Nazwa kategorii: P ($\mathrm{I}$ losowanie)
    Na tym etapie mamy 13 trefli i 39 kart pozostałego koloru.
    Elementy należące do kategorii P ($\mathrm{I}$ losowanie)

    • Nazwa kategorii: T ($\mathrm{II}$ losowanie)

    • Nazwa kategorii: P ($\mathrm{II}$ losowanie)

Jeżeli wylosujemy dwa trefle, to liczba wyników wynosi:
$13·13=169$.
Jeżeli wylosujemy jednego trefla, to liczba wyników wynosi:
$13·39+39·13=507+507=1014$
Wobec tego, jeżeli losujemy dwie karty ze zwracaniem i mamy wybrać co najmniej jednego trefla, to liczba wszystkich możliwych wyników wynosi:
$169+1014=1183$

dział matematyki, zajmujący się zbiorami skończonymi oraz odwzorowaniami między nimi

procedura, którą można powtarzać wielokrotnie, mająca określony zbiór wyników

przy wyborze pewnego elementu z dwóch zbiorów, z których pierwszy ma $m$ elementów, a drugi $n$ elementów oraz żaden element nie jest wspólny dla obu tych zbiorów, można to zrobić na $m+n$ sposobów