Prędkość i jej jednostki. Odczytywanie prędkości i drogi z wykresów
Bardzo często używasz pojęć szybkość lub prędkość. Mówisz: „Ten samochód porusza się szybciej, a tamten – wolniej (albo jeden porusza się z dużą prędkością, a drugi – z małą)”. Kiedy spacerujesz, poruszasz się z mniejszą prędkością, niż kiedy biegniesz po boisku. Kiedy obserwujesz wskazania prędkościomierza w samochodzie, widzisz, że się one zmieniają. Czy zastanawiałeś się, czym jest prędkość?

uzasadnić na podstawie przykładów, że ruch ciał jest pojęciem względnym;
podać przykłady układów odniesienia dla danego ruchu;
podać, w jakich sytuacjach używamy pojęcia „punkt materialny”;
wymienić wielkości opisujące ruch;
dokonać klasyfikacji ruchów ze względu na ich tor.
odróżniać prędkość średnią od prędkości chwilowej;
wzorów na prędkość średnią i chwilową;
posługiwać wykresami zależności prędkości od czasu oraz drogi od czasu;
wyrażać prędkość w różnych jednostkach.
1. Prędkość średnia i prędkość chwilowa
Kiedy obserwujesz przejeżdżające samochody, możesz zauważyć, że niektóre z nich pokonują te same odcinki drogi w krótszym czasie niż inne auta. Mówisz wówczas, że niektóre samochody poruszały się z większą prędkością. Kiedy jednak opisujesz ruch tych samochodów, widzisz również, że jedne z nich mogą jechać w jedną stronę, a inne – w stronę przeciwną, ale wzdłuż tej samej drogi. Aby opisać ich ruch, nie wystarczy więc powiedzieć, że prędkość wynosi np. 60 km/h. Istotne jest to, wzdłuż jakiej drogi i w którą stronę poruszał się samochód, czyli ważne są: kierunek (prosta, wzdłuż której samochód się porusza) i zwrot (w którą stronę tego kierunku porusza się auto). Prędkość jest wielkością wektorową – ma wartość, kierunek i zwrot. Jeżeli nie zależy ci na pełnym opisie ruchu ciała, to używasz pojęcia wartość prędkości. Jest to rzecz jasna wartość wektora prędkości.
– wartość, którą uzyskamy, gdy drogę przebytą przez ciało podzielimy przez czas jej przebycia.
Jeżeli przyjmiemy następujące oznaczenia:
– średnia wartość prędkości;
– droga przebyta z tą wartością prędkość;
– czas trwania ruchu (czas przebycia tej drogi);
to otrzymamy zależność:
Gdy mówimy, że samochód poruszał się z prędkością o średniej wartości 50 km/h, nie mamy wcale na myśli tego, że jego prędkość na każdym odcinku przebytej drogi była stała i wynosiła dokładanie 50 km/h. Prędkość w czasie jazdy na pewno wielokrotnie ulegała zmianie – samochód jechał raz szybciej, raz wolniej, być może zatrzymał się na skrzyżowaniu, żeby ustąpić pierwszeństwa przejazdu. Prędkościomierz w samochodzie pokazuje wartość prędkości, którą auto ma w danej chwili ruchu. Jest to prędkość chwilowaprędkość chwilowa.
– prędkość ciała w danej chwili ruchu.
Rekord świata w sprincie (w 2009 r.) to przebycie 100‑metrowego odcinka w czasie 9,58 s. Wiadomo jednak, że sprinter po starcie nie porusza się od razu z maksymalną prędkością. Na starcie prędkość biegacza wynosi zero, a potem stopniowo rośnie. Maksymalna wartość uzyskana jest po pokonaniu ok. 2/3 dystansu. Wynosi wtedy 45 km/h, czyli 12,5 m/s. Gdyby sprinter biegł cały czas z maksymalną prędkością, to dystans 100 m przebyłby w 8 sekund.
Oblicz średnią wartość prędkości rekordzisty (Usaina Bolta) podczas rekordowego biegu.
Różnice wartości prędkości ciał poruszających się w przyrodzie
W przyrodzie możemy zaobserwować ruchy odbywające się z różnymi prędkościami, np. dryft kontynentów odbywa się z prędkością ok. , a światło w próżni porusza się z prędkością ok. . Jak widać, różnice prędkości mogą być ogromne.
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/D16qgGvX3
Rekord w pływaniu na 100 m stylem dowolnym w 2009 r. należał do Brazylijczyka Césaro Cielo Filho i wynosił 46,91 s. Oblicz prędkość średnią, jaka pozwoliła mu wówczas na ustanowienie rekordu świata i wskaż prawidłową odpowiedź.
- 2,13
- 2,00
- 2,20
- 2,21
- 2,15
- 2,19
- 2,07
- 2,10
- 2,17
Oblicz średnią prędkość rowerzysty, który podzielił swoją trasę na trzy odcinki. Pierwszy, o długości 10 km, pokonał w 0,5 h, drugi, mający 30 km, przebył w ciągu 2 h. Trzeci odcinek, który miał 5 km, przejechał w 0,5 h. Prędkość wyraź zarówno w , jak i w . Niezbędne obliczenia wykonaj w zeszycie.
Rozwiązanie:
Dane:
Szukane:
Wzory:
Obliczenia:
Wyrażenie obliczonej prędkości w :
Odpowiedź: Średnia prędkość rowerzysty wyniosła .
2. Wyrażanie prędkości w różnych jednostkach
Wartość prędkości można podawać w różnych jednostkach. Jednostką prędkości w układzie SI jest metr na sekundę . Czasami ze względu na duże wartości prędkości, jakie osiągają np. samochody, wygodniej jest wyrażać prędkość pojazdu w . Bywa, że chcemy wiedzieć, ile metrów ciało przebywa przez jedną sekundę albo jedną minutę (ślimak przebywa kilka centymetrów w ciągu 1 minuty). W jaki sposób można przeliczyć jedną jednostkę prędkości na inną? Jest na to bardzo prosty sposób.
Przykładowo: dane ciało poruszało się z prędkością o wartości . Jeśli chcemy wyrazić tę wartość w metrach na sekundę, to musimy odpowiedzieć sobie na dwa pytania:
ile metrów przypada na jeden kilometr?
ile sekund zawiera jedna godzina?
Oczywiście, i .
Gdy zamienimy kilometr na metry, a godzinę – na sekundy, to po wykonaniu obliczeń otrzymamy:
Dzięki zamianie jednostek i prostym obliczeniom otrzymalismy prędkość wyrażoną w jednostkach układu SI, czyli w .
Podobnie postępujemy, gdy chcemy wyrazić np. w . Podczas przekształcania jednostek zawsze należy zastanowić się, jaką częścią nowej jednostki jest stara jednostka danej wielkości fizycznej.
W przeliczaniu jednostek pomocna jest poniższa aplikacja.
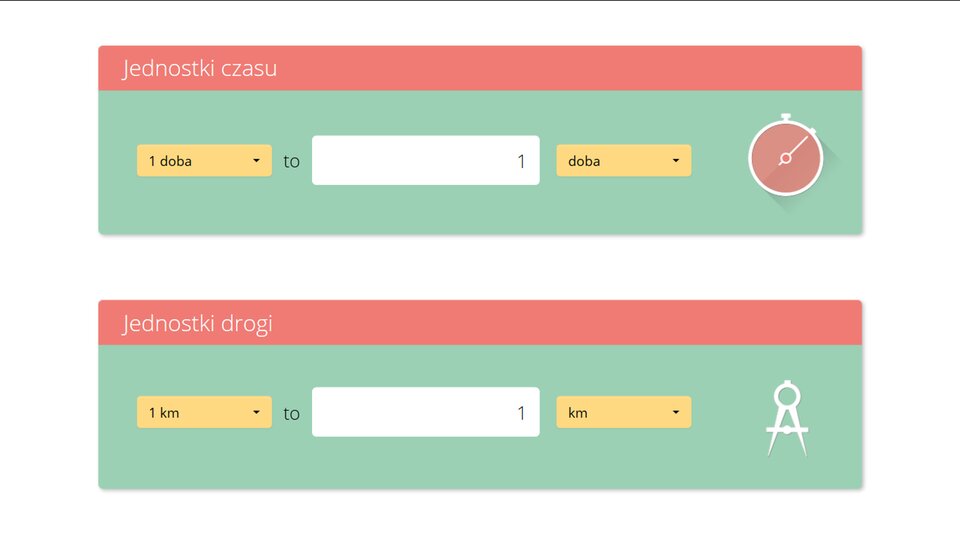
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/D16qgGvX3
Dopasuj do siebie takie same wartości prędkości wyrażone w różnych jednostkach.
<span aria-label="zero przecinek jeden pięć początek ułamka, km, mianownik, s, koniec ułamka" role="math"><math><mrow><mn>0,15</mn><mtext> </mtext><mfrac><mn>km</mn><mn>s</mn></mfrac></mrow></math></span>, <span aria-label="dwadzieścia początek ułamka, m, mianownik, s, koniec ułamka" role="math"><math><mrow><mn>20</mn><mtext> </mtext><mfrac><mn>m</mn><mn>s</mn></mfrac></mrow></math></span>, <span aria-label="sto dziewięćdziesiąt dwa początek ułamka, cm, mianownik, doba, koniec ułamka" role="math"><math><mrow><mn>192</mn><mtext> </mtext><mfrac><mn>cm</mn><mn>doba</mn></mfrac></mrow></math></span>, <span aria-label="zero przecinek zero jeden początek ułamka, m, mianownik, s, koniec ułamka" role="math"><math><mrow><mn>0,01</mn><mtext> </mtext><mfrac><mn>m</mn><mn>s</mn></mfrac></mrow></math></span>, <span aria-label="pięćdziesiąt cztery początek ułamka, km, mianownik, h, koniec ułamka" role="math"><math><mrow><mn>54</mn><mtext> </mtext><mfrac><mn>km</mn><mn>h</mn></mfrac></mrow></math></span>
3. Wykres zależności wartości prędkości i drogi od czasu
Wielkości fizyczne opisujące zjawiska lub procesy fizyczne wygodniej jest przedstawiać w formie graficznej. Kiedy opisujemy ruch, najczęściej przedstawiamy graficznie zależność przebytej drogi od czasu s(t), a także sporządzamy wykresy ilustrujące zależność wartości prędkości od czasu v(t).
Przebyta droga, czas i prędkość to wielkości ściśle ze sobą związane. Aby się o tym przekonać, zagraj w grę. Spróbuj przetrwać na torze wyścigowym i jednocześnie obserwuj, jak zmieniają się droga i prędkość twojego ruchu.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/D16qgGvX3
Na podstawie poniższego wykresu uzupełnij zdania.
Bieg odbywał się na dystansie ............ m. Biegacz pokonał swój dystans w czasie ............ s. Sportowiec w czasie 8 sekund przebył drogę ............ metrów.
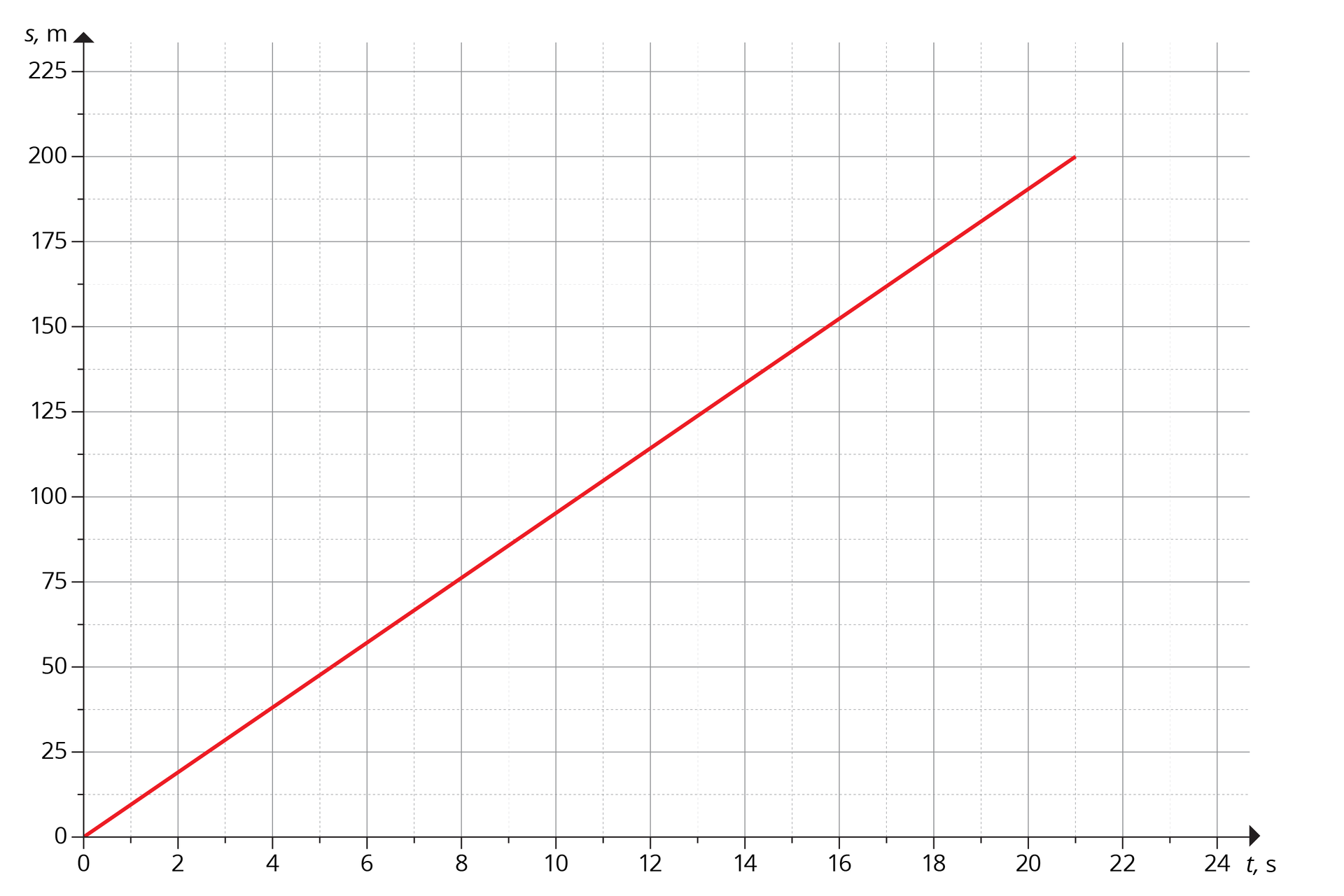
Podsumowanie
Jeżeli drogę przebytą przez ciało podzielimy przez czas jej przebycia, to obliczymy średnią wartość prędkości. Oblicza się ją za pomocą wzoru:
gdzie:
– prędkość średnia;
– droga przebyta przez ciało;
– czas przebycia drogi (przedział czasu).
Prędkość chwilowa to prędkość ciała w danej chwili ruchu (w bardzo krótkim przedziale czasu). Jeśli dokonujemy pomiarów prędkości w długim przedziale czasu, to prędkość średnia zwykle znacznie różni się od prędkości chwilowych. Gdy przedział czasu jest bardzo mały (dąży do zera), to prędkość średnia zbliża się do prędkości chwilowej.
Aby przedstawić graficznie zależności pomiędzy wielkościami fizycznymi opisującymi zjawiska lub procesy, posługujemy się wykresami. Wykres zależności drogi od czasu opisujemy jako s(t), a zależność wartości prędkości od czasu – jako v(t). Wykresy niosą wiele interesujących informacji dotyczących przebiegu zjawisk fizycznych. Zawsze, jeśli to możliwe, korzystaj z wykresów!
Na podstawie poniższego wykresu oblicz prędkość trzech ciał na poszczególnych etapach trwania ruchu (w przedziałach 0–4 sekund oraz 4–6 sekund). Jaka jest zależność pomiędzy kątem nachylenia wykresu do osi czasu a wartością prędkości ciał na danym odcinku drogi?

Na podstawie poniższego wykresu oblicz drogę przebytą przez ciała M, N i O oraz ich średnią prędkość.
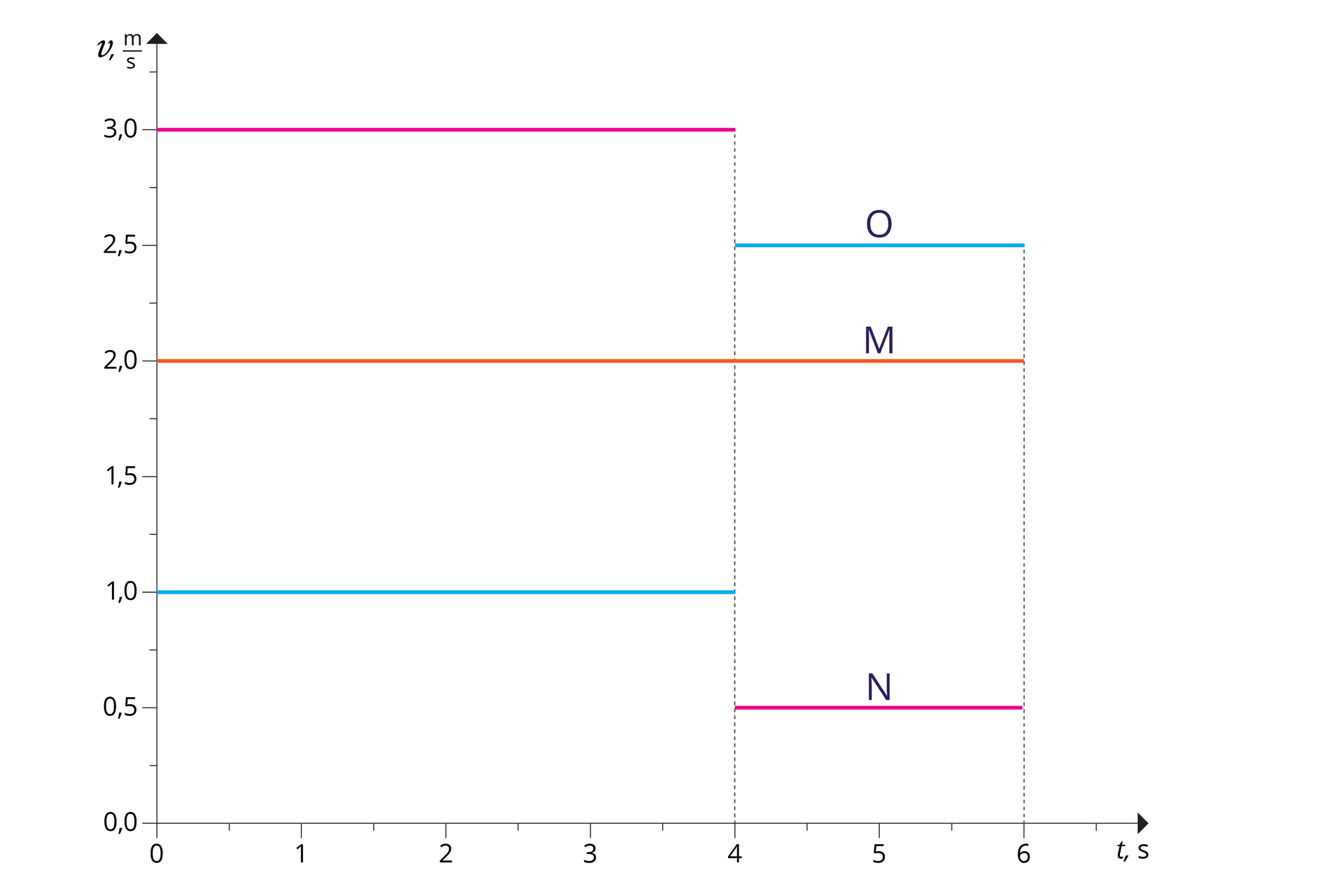
Przelicz wartość prędkości na odpowiednie jednostki:
…
…
…
…
Pomiary w fizyce. Niepewność pomiaru. Przeliczanie wielokrotności i podwielokrotnościPomiary w fizyce. Niepewność pomiaru. Przeliczanie wielokrotności i podwielokrotności
Ruch i spoczynek. Względność ruchuRuch i spoczynek. Względność ruchu
Zadania podsumowujące
Uzupełnij luki.
Królik przebiegł 100 m w czasie 8 s. Wartość jego prędkości wynosiła ............ .
Samochód przejechał 2 km w czasie 0,05 h. Jego wartość prędkości wynosiła ............ .
Samolot myśliwski przeleciał 2000 m w czasie 0,24 min. Jego wartość prędkości wynosiła ............ .