Przykład 1

Zdarza się, że w wypowiedziach dotyczących przewidywania wyniku jakiegoś zdarzenia szacowany jest wynik tego zdarzenia. Spotykamy się więc z następującymi sformułowaniami „po pierwszym meczu nasze szanse na awans oceniam na $75$ procent” czy „sądzę, że moje szanse na pierwszą nagrodę są mniejsze niż jeden do dziesięciu”, czy też „jestem przekonany, że zachwyt przy ocenie naszej oferty wyrazi co najmniej dwóch na trzech klientów naszego sklepu”.
Podając liczby: $\frac{3}{4}$ , $\frac{1}{10}$ , $\frac{2}{3}$ oceniamy, na ile zajście zdarzenia, którego wynik nie jest znany, jest zbliżone do prawdy (prawdopodobne).

W tym rozdziale wprowadzimy umowy, które pozwolą nam obliczać prawdopodobieństwa zdarzeń w pewnych nieskomplikowanych sytuacjach przy zastosowaniu formalnie opisanych metod. W przykładach będziemy analizować wyniki doświadczeń losowych.

Przykład 2

Każdy z nas spotkał się z sytuacją, w której przy podjęciu pewnej decyzji wybieramy wynik losowania. Na przykład w amerykańskiej zawodowej lidze koszykówki NBA nabór nowych zawodników odbywa się w tak zwanej loterii draftowej. Według obowiązujących przepisów przystępuje do niej $14$ zespołów z najgorszym bilansem zwycięstw z poprzedniego sezonu, przy czym zespoły te są ustawiane w kolejności od najgorszego bilansu do najlepszego. W tej loterii losuje się spośród $1000$ kul, przy czym $250$ z nich przydzielonych jest pierwszemu zespołowi z tego zestawienia, $199$ – drugiemu, a $138$ – trzeciemu itd. W ten sposób najgorszy zespół ma $25 %$ szans na wylosowanie pierwszego numeru. Powiemy więc, że prawdopodobieństwo, że najgorszy zespół wylosuje pierwszy numer w loterii draftowej jest równe $\frac{1}{4}$ .
Jednak największe szanse nie gwarantują pierwszego numeru w takiej loterii. W $2008$ roku pierwszy numer w drafcie wylosowała drużyna Chicago Bulls, która w losowaniu miała przydzielone $17$ kul. Zatem przed losowaniem ocenilibyśmy prawdopodobieństwo, że właśnie ta drużyna wylosuje pierwszy numer jako równe $\frac{17}{1000}$ .

Pojęcie prawdopodobieństwa

R138vRb8FndWA1

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1Pnzh2kUgJD11

RMJplr7CJEyUM1

RqBE4zhYpWDnL1

RP3en70RFs5SG1

RPDoHpXSlkZr81

RUAPY9AwGG0Pg1

iz3aPJUGz3_d5e145

Przykład 3

W pewnej szóstej klasie dawno temu spotkali się trzej uczniowie: Janek, Piotrek i Andrzej. Zdarzyło się, że wszyscy korzystali z obiadów w szkolnej stołówce. Do każdego obiadu był tam serwowany deser. Na początku roku szkolnego Janek zaproponował Piotrkowi następującą zabawę: „Do końca roku szkolnego będziemy przychodzili na obiady. Niech w tym czasie o podziale naszych deserów zdecyduje los. Codziennie przed obiadem Andrzej rzuci dwa razy monetą. Jeśli raz wypadnie orzeł i raz wypadnie reszka, to ja zjem dwa desery: twój i mój. Jeśli dwa razy wypadnie orzeł, to Ty zjesz te dwa desery. Natomiast jeśli wypadnie dwa razy reszka, to każdy zje swój deser. Jak widzisz, umowa jest uczciwa, bo poza tymi trzema przypadkami innego wyniku dwóch rzutów monetą nie ma, a patrząc na te przypadki łącznie, każdy z nas ma równe szanse. Ja w jednym przypadku dostanę dwa desery, w drugim – żadnego, a w trzecim – jeden. I ty także: w jednym przypadku dostaniesz dwa desery, w innym – żadnego, a w jeszcze innym – jeden. Nie pomyśl sobie, że w zmowie z Andrzejem szykujemy jakąś sztuczkę z monetą. Gdybyś chciał, to możemy się umówić, że monetę do rzucania będziemy wybierali wspólnie, a przy rzucaniu będziemy się zmieniali. To jak, zgadzasz się na taki układ? Mielibyśmy niezłą zabawę przed obiadem.”
Piotrek chwilę pomyślał, a następnie odmówił. Od razu też wytłumaczył Jankowi, dlaczego uważa, że taka umowa wcale nie jest uczciwa.

Podamy argumenty, które przemawiają za tym, że Piotrek powinien odrzucić pomysł Janka.
Dwukrotny rzut monetą to doświadczenie, które polega na wykonaniu po kolei dwóch czynności. Każda z nich może skończyć się na jeden z dwóch sposobów: albo wypadnie orzeł, albo wypadnie reszka. Na podstawie reguły mnożenia stwierdzamy, że liczba wszystkich możliwych wyników dwukrotnego rzutu kostką jest równa

2 \cdot 2 = 4 .

Wszystkie wyniki takiego doświadczenia można przedstawić w tabeli

Tabela. Dane
$I$ rzut/ $II$ rzuty	Orzeł	Reszka
orzeł	(orzeł, orzeł)	(orzeł, reszka)
reszka	(reszka, orzeł)	(reszka, reszka)

Lub za pomocą drzewa:

RUurLeg8NNmaM1

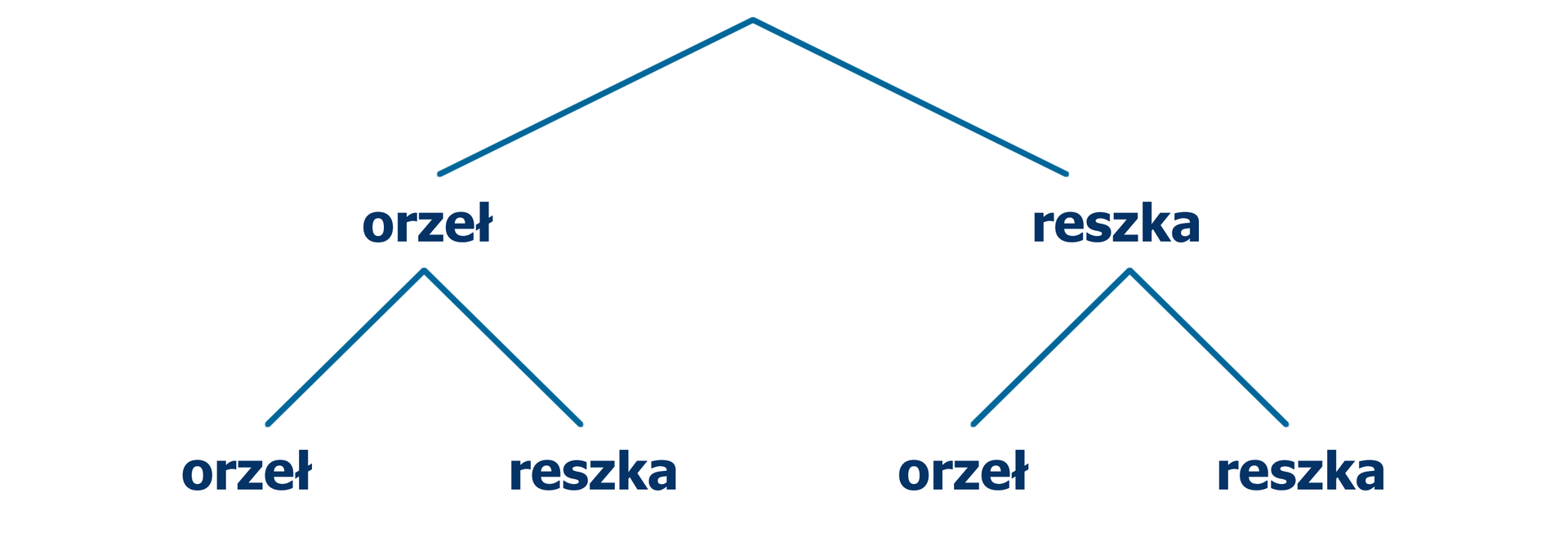
Rysunek schematu w postaci drzewa, który ilustruje wyniki doświadczenia dwukrotnego rzutu monetą. Pierwszy rzut – odchodzą dwie gałęzie: orzeł i reszka. Od gałęzi orzeł w drugim rzucie odchodzą gałęzie: orzeł i reszka. Od gałęzi reszka w drugim rzucie odchodzą gałęzie: orzeł i reszka. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Z tabeli możemy też odczytać dwuelementowe ciągi, które opisują wszystkie możliwe wyniki dwukrotnego rzutu monetą:
(orzeł, orzeł), (orzeł, reszka), (reszka, orzeł), (reszka, reszka).
Są więc dokładnie cztery możliwe wyniki dwukrotnego rzutu monetą. Pewnie i bez powyższego opisu potrafi to uzasadnić każdy, kto zrozumiał podstawowe zasady obowiązujące w kombinatoryce (omawialiśmy je w poprzednich rozdziałach).
Typowa moneta znajdująca się w obiegu może być uznana za symetryczną. Oznacza to, że przy dużej liczbie rzutów taką monetą średnio połowa z nich skończy się wyrzuceniem orła, a połowa – reszki. Zatem i każdy z czterech wyników dwukrotnego rzutu monetą będzie wypadał średnio tak samo często, jak każdy z pozostałych.

Wracamy do zabawy opisanej w poprzednim przykładzie. Jak już zauważyliśmy: wbrew sugestiom Janka mamy do rozpatrzenia nie trzy, a cztery przypadki. Popatrzmy na rozdział deserów w każdym z tych przypadków:

(orzeł, orzeł) – Piotrek zje dwa desery, Janek – żadnego,
(orzeł, reszka) – Piotrek nie zje żadnego deseru, a Janek zje dwa,
(reszka, orzeł) – Piotrek nie zje żadnego deseru, a Janek zje dwa,
(reszka, reszka) – Piotrek zje jeden deser i Janek zje jeden deser.

Wobec tego w ciągu kolejnych czterech dni, kiedy chłopcy mają do rozdzielenia $8$ deserów, $5$ deserów zje Janek, a tylko trzy – Piotrek. Zatem kontynuowanie przez dłuższy czas losowego wyboru deserów metodą zaproponowaną przez Janka jest dla Piotrka zdecydowanie niekorzystne.

Podając te wartości, oceniliśmy jedynie szanse każdego z chłopców na otrzymanie deseru. Nie należy się jednak spodziewać, że w ciągu dowolnie wybranych czterech dni, przy takiej metodzie losowego rozdziału deserów, Piotrek dostanie dokładnie $3$ z ośmiu możliwych do otrzymania. Natomiast przy przeprowadzeniu większej liczby powtórzeń tego doświadczenia liczba deserów przeznaczonych dla Piotrka będzie zbliżała się do pewnej wartości, którą nazywamy prawdopodobieństwem zdarzenia, że w wyniku podanej metody przydziału deser dostanie Piotrek.
Można formalnie wykazać, że $3$ to oczekiwana liczba deserów, które w ciągu czterech dni otrzyma Piotrek, gdyby zastosował się do metody zaproponowanej przez Janka. Metody matematyczne, których do tego celu należałoby użyć, stosowane są w rachunku prawdopodobieństwa.

Przykład 4

Każdy oficjalny mecz piłki nożnej zaczyna się od losowania drużyny, która rozpocznie rozgrywkę. Sędzia rzuca wtedy monetą, przy czym robi to w taki sposób, żeby nikt nie miał wątpliwości, że wynik takiego losowania będzie przypadkowy. Przed takim losowaniem jesteśmy przekonani, że obie zainteresowane drużyny mają równe szanse rozpoczęcia gry od środka boiska.
Za każdym razem takie losowanie uznamy więc za doświadczenie losowe.
Kilkuosobową grę w karty rozpoczyna się od wyboru osoby rozdającej. Chcemy, aby metoda wyboru dawała równe szanse każdemu z graczy. Jednym ze sposobów jest losowanie przez każdego z graczy jednej karty z pełnej talii. Zazwyczaj rozdającym zostaje ta osoba, która wylosuje kartę najniższą według rangi w danej grze.
Taki wybór osoby rozdającej uznamy także za doświadczenie losowe.
Przypuśćmy, że o wyborze kapitana w przypadkowo dobranej pięcioosobowej drużynie koszykówki chcemy zadecydować losowo – możemy to zrobić, przygotowując wcześniej losy. Wystarczy w tym celu wziąć pięć takich samych kartek papieru, cztery pozostawić puste, a na jednej z nich postawić umówiony znak lub napisać słowo „kapitan”. Następnie złożyć kartki w podobny sposób i wrzucić do takiego pojemnika, z którego gracze losują po jednej kartce, nie widząc wybieranego przedmiotu. Kapitanem zostaje ten z nich, który wylosuje wyróżnioną kartkę.

W prezentowanych w tym rozdziale przykładach będziemy zajmować się doświadczeniami, które (podobnie jak przywołane powyżej) możemy uznać za losowe. Przedmioty używane w opisywanych doświadczeniach są powszechnie dostępne, więc każdy może samodzielnie takie doświadczenie przeprowadzić tyle razy, ile tylko uzna za stosowne. Naszym głównym zadaniem będzie jednak takie opisanie modelu przeprowadzanego doświadczenia, aby dla ustalenia prawdopodobieństwa otrzymania konkretnego wyniku wystarczyło zrozumienie podstawowych zasad rządzących rachunkiem prawdopodobieństwa.

Wprowadzimy podstawowe pojęcia, którymi będziemy się posługiwać przy obliczaniu prawdopodobieństw.

Każdy możliwy wynik, który może pojawić się w doświadczeniu losowym, będziemy nazywać zdarzeniem elementarnym.

Przykład 5

W doświadczeniu losowym, polegającym na dwukrotnym rzucie symetryczną monetą, rozróżnimy cztery zdarzenia elementarne:

„za pierwszym razem wypadł orzeł, a za drugim razem wypadł orzeł”, co w skrócie zapiszemy jako dwuelementowy ciąg wyników (orzeł, orzeł),
„za pierwszym razem wypadł orzeł, a za drugim razem wypadła reszka”, co w skrócie zapiszemy jako (orzeł, reszka),
„za pierwszym razem wypadła reszka i za drugim razem wypadł orzeł”, co w skrócie zapiszemy jako (reszka, orzeł),
„za pierwszym razem wypadła reszka i za drugim razem wypadła reszka”, co w skrócie zapiszemy jako (reszka, reszka).

W omawianym doświadczeniu używaliśmy monety symetrycznej, więc spodziewamy się, że przy dużej liczbie powtórzeń każde z wypisanych powyżej zdarzeń elementarnych pojawi się z podobną średnią częstością. Uznajemy zatem, że wszystkie te zdarzenia elementarne są jednakowo prawdopodobne.
Zbiór wszystkich zdarzeń elementarnych będziemy oznaczali za pomocą dużej greckiej litery $Ω$ (omega).
Fakt, że w rozpatrywanym doświadczeniu zbiór zdarzeń elementarnych
$Ω = {$ (orzeł, orzeł), (orzeł, reszka), (reszka, orzeł), (reszka, reszka)}
liczy cztery elementy, zapiszemy symbolicznie $| Ω | = 4$ .

W rozwiązaniach kilku kolejnych przykładowych zadań będziemy wypisywali zdarzenia elementarne i na tej podstawie określali zbiór $Ω$ wszystkich zdarzeń elementarnych i liczbę jego elementów.

iz3aPJUGz3_d5e284

Zdarzenie

Definicja: Zdarzenie

Dowolny podzbiór zbioru $Ω$ będziemy nazywać zdarzeniem, a elementy takiego podzbioru będziemy nazywać zdarzeniami elementarnymi sprzyjającymi temu zdarzeniu.
Zbiór pusty, czyli zdarzenie, któremu nie sprzyja żadne zdarzenie elementarne, nazywamy zdarzeniem niemożliwym.
Zbiór $Ω$ , czyli zdarzenie, któremu sprzyja każde zdarzenie elementarne, nazywamy zdarzeniem pewnym.

Przykład 6

Ponieważ w doświadczeniu rozpatrywanym w poprzednim przykładzie zbiór $Ω$ ma cztery elementy, to różnych zdarzeń w tym doświadczeniu jest $2^{4} = 16$ (tyle jest bowiem wszystkich podzbiorów czteroelementowego zbioru $Ω)$ .
Przykładowymi zdarzeniami w doświadczeniu losowym, polegającym na dwukrotnym rzucie symetryczną monetą są:

$A = {$ (orzeł, reszka), (reszka, orzeł)}. Takiemu zdarzeniu sprzyjają dwa zdarzenia elementarne, więc zapiszemy, że $| A | = 2$ . Zdarzenie to można byłoby opisać słownie, np. tak: $A -$ zdarzenie polegające na tym, że wypadło tyle samo orłów, co reszek.
$B = {$ (orzeł, orzeł), (orzeł, reszka), (reszka, orzeł)}. Temu zdarzeniu sprzyjają trzy zdarzenia elementarne, zatem $| B | = 3$ . Zdarzenie to można byłoby opisać słownie, np. tak: $B -$ zdarzenie polegające na tym, że wypadł co najmniej jeden orzeł.
$C = {$ (reszka, reszka)}. Temu zdarzeniu sprzyja jedno zdarzenie elementarne, stąd $| C | = 1$ . Zdarzenie to można byłoby opisać słownie, np. tak: $C -$ zdarzenie polegające na tym, że wypadło mniej orłów niż reszek.

Rozpatrzmy zdarzenia opisane słownie:

$D -$ zdarzenie polegające na tym, że wypadło trzy razy więcej orłów niż reszek. Zbiór $D$ jest pusty – nie ma zdarzeń elementarnych, które sprzyjają temu zdarzeniu. Zdarzenie $D$ jest więc niemożliwe.
$E -$ zdarzenie polegające na tym, że wypadła parzysta liczba orłów. Zdarzeniu $E$ sprzyjają dwa zdarzenie elementarne: (orzeł, orzeł), (reszka, reszka), zatem zapiszemy $E = {$ (orzeł, orzeł), (reszka, reszka) $}$ , a co za tym idzie: $| E | = 2 .$
$F$ – zdarzenie, że wypadły co najwyżej dwie reszki. Zdarzeniu $F$ sprzyjają wszystkie zdarzenia elementarne, zatem zapiszemy $F = Ω$ . Oznacza to, że $F$ jest zdarzeniem pewnym.

Fakt, że zdarzenie $A$ jest podzbiorem zbioru zdarzeń elementarnych $Ω$ zapisujemy też, używając symbolu zawierania zbiorów: $A \subset Ω$ .

Określimy teraz, jak będziemy obliczać prawdopodobieństwo w tak zwanym schemacie klasycznym.

Klasyczna definicja prawdopodobieństwa

Twierdzenie: Klasyczna definicja prawdopodobieństwa

Rozpatrzmy doświadczenie losowe, w którym wszystkie zdarzenia elementarne są jednakowo prawdopodobne, a $Ω$ jest zbiorem wszystkich zdarzeń elementarnych.
Prawdopodobieństwem $P (A)$ zdarzenia $A \subset Ω$ nazywamy wówczas iloraz liczby zdarzeń elementarnych sprzyjających zdarzeniu $A$ przez liczbę wszystkich zdarzeń elementarnych:

P (A) = \frac{|A|}{|Ω|} .

Przykład 7

W doświadczeniu losowym polegającym na dwukrotnym rzucie symetryczną monetą wszystkie zdarzenie elementarne są jednakowo prawdopodobne. Zatem obliczając prawdopodobieństwa zdarzeń, możemy skorzystać z definicji klasycznej. Obliczymy w ten sposób prawdopodobieństwa zdarzeń opisanych w poprzednim przykładzie.
Przypomnijmy, że w tym doświadczeniu $| Ω | = 4$ . Oznacza to, że:

jeżeli $A = {($ orzeł, reszka), (reszka, orzeł $)}$ , to $P (A) = \frac{|A|}{|Ω|} = \frac{2}{4} = \frac{1}{2}$ ,
jeżeli $B = {($ orzeł, orzeł), (orzeł, reszka), (reszka, orzeł $)}$ , to $P (B) = \frac{|B|}{|Ω|} = \frac{3}{4}$ ,
jeżeli $C = {($ reszka, reszka $)}$ , to $P (C) = \frac{|C|}{|Ω|} = \frac{1}{4}$ ,
jeżeli $D$ to zdarzenie, że wypadło trzy razy więcej orłów niż reszek, to $D = \emptyset$ , stąd $P (D) = \frac{|D|}{|Ω|} = \frac{0}{4} = 0$ ,
jeżeli $E$ to zdarzenie, że wypadła parzysta liczba orłów, to $E = {($ orzeł, orzeł), (reszka, reszka $)}$ , stąd $P (E) = \frac{|E|}{|Ω|} = \frac{2}{4} = \frac{1}{2}$ ,
jeżeli F to zdarzenie, że wypadły co najwyżej dwie reszki, to $F = Ω$ , stąd $P (F) = \frac{|F|}{|Ω|} = \frac{4}{4} = 1$ .

Warto zapamiętać dwa wnioski wynikające z klasycznej definicji prawdopodobieństwa:

$P (\emptyset) = \frac{|\emptyset|}{|Ω|} = \frac{0}{|Ω|} = 0$ , co oznacza, że prawdopodobieństwo zdarzenia niemożliwego jest równe $0$ ,
$P (Ω) = \frac{|Ω|}{|Ω|} = 1$ , co oznacza, że prawdopodobieństwo zdarzenia pewnego jest równe $1$ .

iz3aPJUGz3_d5e415

Własności prawdopodobieństwa

Przykład 8

W kopercie znajduje się $11$ kartek, ponumerowanych od $1$ do $11$ . Z tej koperty wybieramy losowo jedną kartkę. Obliczymy prawdopodobieństwo otrzymania:

liczby podzielnej przez $4$ ,
liczby niepodzielnej przez $4$ .

Za zdarzenie elementarne w takim doświadczeniu przyjmujemy wylosowanie jednej spośród $11$ kartek. Ponieważ wylosowana kartka jest jednoznacznie przypisana do zapisanego na niej numeru, więc nie doprowadzimy do żadnych nieporozumień, kiedy zbiór wszystkich zdarzeń elementarnych zapiszemy skrótowo

Ω = \{1,2, 3,4, 5,6, 7,8, 9,10,11\} .

Mamy więc $|Ω| = 11$ .
Oznaczmy
$A$ – zdarzenie polegające na tym, że wylosowano liczbę podzielną przez $4$ ,
$B$ – zdarzenie polegające na tym, że wylosowano liczbę niepodzielną przez $4$ .
Wszystkie zdarzenia elementarne są jednakowo prawdopodobne, wobec tego przy obliczaniu prawdopodobieństw zdarzeń $A, B, C$ skorzystamy z definicji klasycznej.

Wśród liczb ze zbioru $Ω$ znajdujemy liczby podzielne przez $4$ – są to $4$ oraz $8$ , zatem możemy zapisać skrótowo, że $A = \{4, 8\}$ . Oznacza to, że są dwa zdarzenia elementarne, które sprzyjają zdarzeniu $A$ , więc $|A| = 2$ . Stąd $P (A) = \frac{|A|}{|Ω|} = \frac{2}{11}$ .
Wśród liczb ze zbioru $Ω$ znajdujemy wszystkie liczby niepodzielne przez $4$ . Zapisujemy zbiór zdarzeń elementarnych sprzyjających zdarzeniu $B :$ $B = \{1,2, 3,5, 6,7, 9,10,11\}$ . Stąd $|B| = 9$ , a więc

P (B) = \frac{|B|}{|Ω|} = \frac{9}{11} .

Zauważmy, że do opisanego zbioru $B$ należą wszystkie zdarzenia elementarne, które nie sprzyjają zdarzeniu $A$ (możemy też powiedzieć, że zbiór $B$ jest dopełnieniem zbioru $A$ do zbioru $Ω)$ .
Taką zależność między dwoma zdarzeniami opisuje się za pomocą pojęcia zdarzenia przeciwnego.

zdarzenie przeciwne

Definicja: zdarzenie przeciwne

Zdarzeniem przeciwnym do zdarzenia $A$ , należącego do zbioru zdarzeń elementarnych $Ω$ , nazywamy takie zdarzenie $A’$ należące do $Ω$ , któremu sprzyjają wszystkie zdarzenia elementarne, które nie sprzyjają zdarzeniu $A$ .
Z tej definicji wynika, że również zdarzenie $A$ jest zdarzeniem przeciwnym do $A’$ .

Zauważmy, że ponieważ zdarzenia $A$ i $A’$ są rozłączne $(A \cap A' = \emptyset)$ oraz ich sumą jest zbiór wszystkich zdarzeń elementarnych $Ω (A \cup A' = Ω)$ , więc liczba wszystkich zdarzeń elementarnych jest sumą liczb zdarzeń elementarnych sprzyjających zdarzeniu $A$ oraz zdarzeń elementarnych sprzyjających zdarzeniu $A’$ .

|Ω| = |A| + |A'|

Jeśli obie strony otrzymanej równości podzielimy przez liczbę dodatnią $|Ω|$ , to otrzymamy

\frac{|Ω|}{|Ω|} = \frac{|A|}{|Ω|} + \frac{|A'|}{|Ω|}

Ponieważ $A$ oraz $A’$ są zdarzeniami ze zbioru $Ω$ , więc liczba $\frac{|A|}{|Ω|}$ to prawdopodobieństwo zdarzenia $A$ , natomiast liczba $\frac{|A'|}{|Ω|}$ to prawdopodobieństwo zdarzenia $A’$ . Stąd

P (A) + P (A') = 1 .

Prawdziwe jest zatem twierdzenie.

o prawdopodobieństwie zdarzenia przeciwnego

Twierdzenie: o prawdopodobieństwie zdarzenia przeciwnego

Załóżmy, że $A$ jest zdarzeniem ze zbioru zdarzeń elementarnych $Ω$ . Wtedy prawdopodobieństwo zdarzenia $A’$ , przeciwnego do $A$ , wyraża się wzorem

P (A') = 1 - P (A) .

Przykład 9

Załóżmy, że w pewnym doświadczeniu losowym dane jest zdarzenie $A$ oraz zachodzi równość $3 \cdot P (A) = 7 \cdot P (A')$ , gdzie $A’$ jest zdarzeniem przeciwnym do $A$ . Obliczymy prawdopodobieństwo zdarzenia $A$ .
Przekształcamy równość daną w treści zadania, korzystając z zależności między $P (A')$ i $P (A)$

3 \cdot P (A) = 7 \cdot (1 - P (A))

3 \cdot P (A) = 7 - 7 \cdot P (A)

10 \cdot P (A) = 7

Stąd wynika, że

P (A) = \frac{7}{10} .

Przykład 10

Ze zbioru dwucyfrowych liczb naturalnych wybieramy losowo jedną liczbę. Obliczymy prawdopodobieństwo, że otrzymana liczba jest podzielna przez $6$ lub przez $10$ .
Za zdarzenie elementarne w takim doświadczeniu przyjmujemy wylosowanie jednej spośród 90 dwucyfrowych liczb naturalnych. Zbiór wszystkich zdarzeń elementarnych zapiszemy

Ω = \{10, 11, 12, . . ., 99\}

sposób $I$

Wypisujemy wszystkie zdarzenia elementarne, które sprzyjają zdarzeniu „otrzymana liczba jest podzielna przez $6$ lub przez $10$ ”:
$\{10, 12, 18, 20, 24, 30, 36, 40, 42, 48, 50, 54, 60, 66, 70, 72, 78, 80, 84, 90, 96\}$ .
Jest ich $21$ .
Korzystając z definicji klasycznej, stwierdzamy więc, że szukane prawdopodobieństwo jest równe $\frac{21}{90} = \frac{7}{30}$ .

sposób $II$

Oznaczmy:
$A$ – zdarzenie, że wylosowano liczbę podzielną przez 6,
$B$ – zdarzenie, że wylosowano liczbę podzielną przez 10.
Zatem
$A = \{12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84, 90, 96\}$ ,
$B = \{10, 20, 30, 40, 50, 60, 70, 80, 90\}$ .
Zdarzenie, którego prawdopodobieństwo mamy obliczyć: „otrzymana liczba jest podzielna przez $6$ lub przez $10$ ”, to suma zdarzeń $A$ oraz $B$ .
Zdarzenia A i B nie są rozłączne, a ich część wspólna to zdarzenie

A \cap B = \{30, 60, 90\}

Przy obliczeniu zadanego prawdopodobieństwa skorzystamy ze wzoru na liczbę elementów sumy dwóch zbiorów

|A \cup B| = |A| + |B| - |A \cap B|

Ponieważ $|A| = 15, |B| = 9$ i $|A \cap B| = 3$ , to $|A \cup B| = |A| + |B| - |A \cap B| = 15 + 9 - 3 = 21$ .
Oznacza to, że prawdopodobieństwo zdarzenia $A \cup B$ jest równe

P (A \cup B) = \frac{|A \cup B|}{|Ω|} = \frac{21}{90} = \frac{7}{30} .

Zauważmy, że dla dowolnych zdarzeń $A, B$ ze zbioru zdarzeń elementarnych $Ω$ ze wzoru na liczbę elementów sumy dwóch zbiorów

|A \cup B| = |A| + |B| - |A \cap B|

wynika, że

\frac{|A \cup B|}{|Ω|} = \frac{|A|}{|Ω|} + \frac{|B|}{|Ω|} - \frac{|A \cap B|}{|Ω|} .

Ponieważ $A \cup B$ oraz $A \cap B$ są również zdarzeniami ze zbioru $Ω$ , więc na mocy definicji klasycznej otrzymujemy zależność

P (A \cup B) = P (A) + P (B) - P (A \cap B)

Prawdziwe jest więc twierdzenie.

o prawdopodobieństwie sumy dwóch zdarzeń

Twierdzenie: o prawdopodobieństwie sumy dwóch zdarzeń

Załóżmy, że $A$ oraz $B$ są zdarzeniami ze zbioru zdarzeń elementarnych $Ω$ . Wtedy prawdopodobieństwo sumy $A \cup B$ zdarzeń $A$ oraz $B$ wyraża się wzorem

P (A \cup B) = P (A) + P (B) - P (A \cap B),

gdzie $A \cap B$ to zdarzenie, które jest iloczynem (częścią wspólną) zdarzeń $A, B$ .

Przykład 11

Załóżmy, że w pewnym doświadczeniu dane są zdarzenia $A$ i $B$ , przy czym ich prawdopodobieństwa są równe odpowiednio $\frac{2}{7}$ i $\frac{3}{11}$ . W tym doświadczeniu pewne jest zdarzenie, że zajdzie zdarzenie $A’$ lub zdarzenie $B’$ (gdzie $A’$ oraz $B’$ oznaczają zdarzenia przeciwne do zdarzeń odpowiednio $A$ i $B$ ). Obliczymy prawdopodobieństwo zdarzenia, że zajdzie jednocześnie zdarzenie $A’$ i zdarzenie $B’$ .
Obliczamy

P (A') = 1 - P (A) = 1 - \frac{2}{7} = \frac{5}{7}

oraz

P (B') = 1 - P (B) = 1 - \frac{3}{11} = \frac{8}{11} .

Z treści zadania wiemy, że $P (A' \cup B') = 1$ , a mamy obliczyć prawdopodobieństwo zdarzenia $A' \cap B'$ . Korzystając z twierdzenia o prawdopodobieństwie sumy, zapisujemy $P (A' \cup B') = P (A ') + P (B ') - P (A' \cap B')$ . Stąd prawdopodobieństwo zdarzenia, że zajdzie jednocześnie zdarzenie $A’$ i zdarzenie $B’$ jest równe

P (A' \cap B') = P (A') + P (B') - P (A^{'} \cup B^{'}) = \frac{5}{7} + \frac{8}{11} - 1 = \frac{34}{77} .

Przykład 12

Wśród $216$ uczniów klas maturalnych pewnej szkoły ponadgimnazjalnej przeprowadzono sondaż na temat poczytności dwóch tygodników: „Widoki” oraz „Rokowania”. Okazało się, że tygodnik „Widoki” czytają $144$ osoby, tygodnik „Rokowania” czytają $132$ osoby, a oba te tygodniki czyta $80$ osób.
Obliczymy prawdopodobieństwo p zdarzenia, że osoba wybrana losowo z tej grupy nie czyta żadnego z tych tygodników.
Za zdarzenie elementarne przyjmujemy wylosowanie jednej osoby z grupy ankietowanych uczniów. Zatem $|Ω| = 216$ .
Oznaczmy

$A$ – zdarzenie polegające na tym, że wylosowana osoba czyta tygodnik „Widoki”,
$B$ – zdarzenie, że wylosowana osoba czyta tygodnik „Rokowania”.

|A \cup B| = |A| + |B| - |A \cap B| = 144 + 132 - 80 = 196

Stąd

|Ω| - |A \cup B| = 216 - 196 = 20

to liczba osób, które nie czytają żadnego z tych tygodników.
Oznacza to, że szukane prawdopodobieństwo jest równe

p = \frac{20}{216} = \frac{5}{54} .

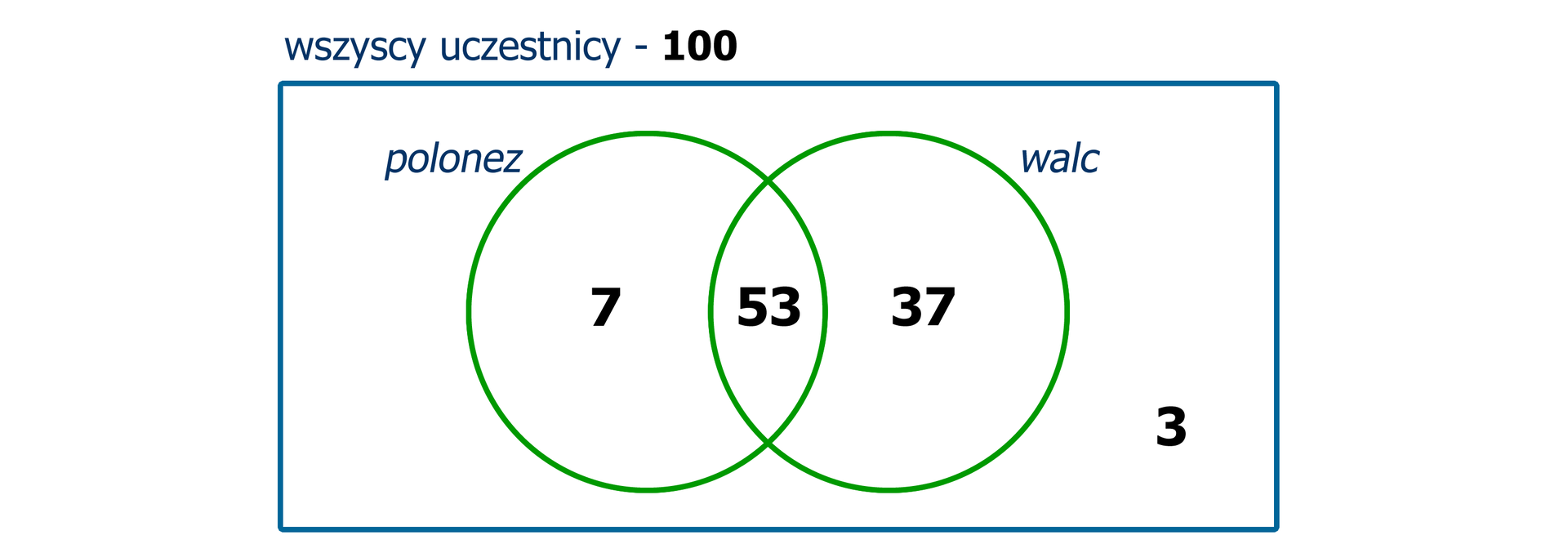
Zależności między liczbami uczniów w tym zadaniu można przedstawić schematycznie za pomocą diagramu.

Rw31ak66N3u2o1

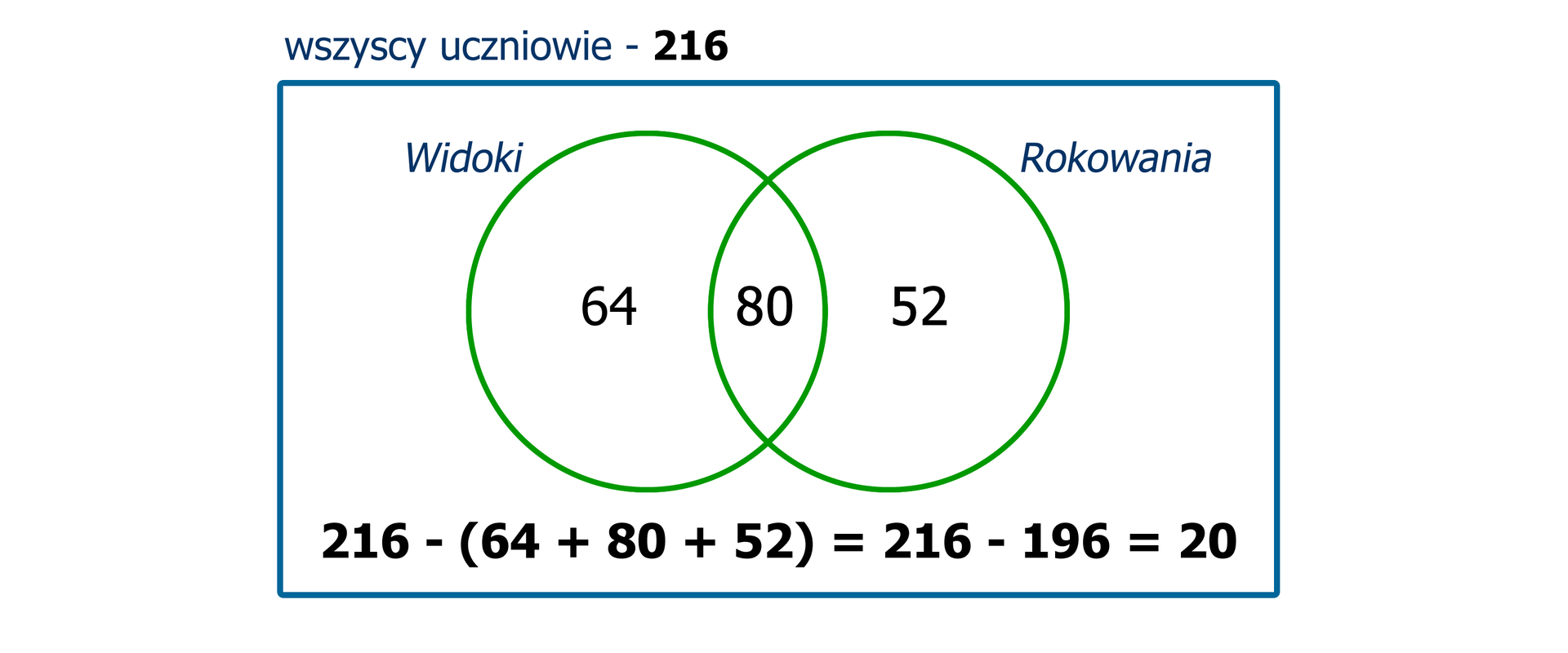
Rysunek dwóch okręgów, które ilustrują zbiory uczniów czytających tygodniki Widoki i Rokowania. Zbiór Widoki zawiera elementy – 64 i 80. Zbiór Rokowania zawiera elementy – 52 i 80. Część wspólna zbiorów 80. Zapis: wszystkich uczniów 216. Działanie: 216 -(64 + 80 +52) =216 -196 =20 — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Wpisaliśmy w nim po kolei

liczbę uczniów, którzy czytają oba tygodniki: $80$ ,
liczbę uczniów, którzy czytają tygodnik „Widoki” i nie czytają tygodnika „Rokowania”: $144 - 80 = 64$ ,
liczbę uczniów, którzy czytają tygodnik „Rokowania” i nie czytają tygodnika „Widoki”: $132 - 80 = 52$ ,
liczbę uczniów, którzy nie czytają żadnego z tych dwóch tygodników: $216 - (64 + 80 + 52) = 20$ .

Przykład 13

Z pudełka zawierającego $8$ kul ponumerowanych od $1$ do $8$ losujemy jednocześnie dwie kule. Obliczymy prawdopodobieństwo zajścia takiego zdarzenia $A$ , że suma wylosowanych liczb jest równa $11$ .
Przedstawimy dwa sposoby opisu zbioru zdarzeń elementarnych w tym doświadczeniu.

sposób $I$

Ponieważ z pudełka zawierającego $8$ kul losujemy jednocześnie dwie kule, więc zdarzenie elementarne zapisujemy jako dwuelementowy podzbiór $\{a, b\}$ zbioru $\{1, 2, 3, 4, 5, 6, 7, 8\}$ . Zatem zdarzeń elementarnych jest tyle, ile dwuelementowych podzbiorów zbioru ośmioelementowego, stąd

|Ω| = \frac{8 \cdot 7}{2} = 28

Zdarzeniu, że suma wylosowanych liczb jest równa $11$ , sprzyjają następujące $3$ zdarzenia elementarne: $\{3, 8\}$ , $\{4, 7\}$ , $\{5, 6\}$ . Wobec tego $|A| = 3$ , co oznacza, że

P (A) = \frac{3}{28} .

sposób $II$

Ponieważ dodawanie jest przemienne, więc suma nie zmieni się, kiedy rozróżnimy kule ze względu na kolejność, w której zostały wylosowane. Każde zdarzenie elementarne zapisujemy wtedy jako dwuelementowy ciąg $(a, b)$ , gdzie $a, b$ są różnymi elementami ze zbioru $\{1, 2, 3, 4, 5, 6, 7, 8\}$ numerów kul znajdujących się w pudełku. Wszystkich zdarzeń elementarnych jest więc

|Ω| = 8 \cdot 7 = 56 .

Zdarzeniu, że suma wylosowanych liczb jest równa $11$ sprzyjają następujące zdarzenia elementarne: $(3, 8)$ , $(4, 7)$ , $(5, 6)$ , $(6, 5)$ , $(7, 4)$ , $(8, 3)$ . Stąd $|A| = 6$ , co oznacza, że

P (A) = \frac{6}{56} = \frac{3}{28} .

iz3aPJUGz3_d5e752

Doświadczenia dwuetapowe - metoda drzewa

Przykład 14

Uczniowie trzeciej klasy otrzymali do rozwiązania zestaw $50$ zadań powtórzeniowych z matematyki. Zadania były ponumerowane od $1$ do $50$ . Pewna ich część to zadania kodowane, a pozostałe to zadania zamknięte.
Ania rozwiązała wszystkie te zadania w ciągu dwóch dni. Pierwszego dnia rozwiązała $60 %$ zadań zestawu, przy czym połowę tych zadań stanowiły zadania kodowane. Wśród zadań rozwiązanych przez Anię drugiego dnia co piąte było kodowane.
Obliczymy, jakie jest prawdopodobieństwo p zdarzenia, że przy losowaniu zadania z tego zestawu otrzymamy zadanie kodowane.

sposób $I$

Za zdarzenie elementarne w opisanym doświadczeniu przyjmujemy wylosowanie jednego spośród $50$ zadań.
Obliczenia liczby zadań kodowanych przeprowadzimy w dwóch etapach.

Obliczymy liczbę zadań rozwiązanych w każdym dniu przez Anię: w pierwszym dniu Ania rozwiązała $60 % \cdot 50 = 30$ zadań, a więc w drugim dniu Ania rozwiązała $20$ zadań (to jest $40 %$ wszystkich).
Obliczymy liczbę zadań kodowanych rozwiązanych przez dziewczynkę pierwszego dnia oraz drugiego dnia.

Pierwszego dnia dziewczynka rozwiązała $15$ zadań kodowanych (jest to połowa z $30$ zadań rozwiązanych w tym dniu), natomiast drugiego dnia Ania rozwiązała $\frac{1}{5} \cdot 20 = 4$ zadania kodowane.
Wobec tego wszystkich zadań kodowanych jest w tym zestawie $15 + 4 = 19$ .
Mamy model klasyczny (zdarzenia elementarne są jednakowo prawdopodobne), co oznacza, że szukane prawdopodobieństwo jest równe

p = \frac{19}{50} .

sposób $II$

Zauważmy, że połowa z $\frac{3}{5}$ wszystkich zadań to zadania kodowane rozwiązane przez Anię pierwszego dnia, a $\frac{1}{5}$ z $\frac{2}{5}$ wszystkich zadań to zadania kodowane rozwiązane przez Anię drugiego dnia.
Zatem zadania kodowane stanowią $\frac{19}{50}$ wszystkich zadań (jak to jest pokazane na diagramie), co oznacza, że szukane prawdopodobieństwo jest równe $p = \frac{19}{50}$ .

R1GRTMDpgcIIJ1

Rysunek prostokąta, który ilustruje prawdopodobieństwo zdarzenia, że przy losowaniu zadania z zestawu otrzymamy zadanie kodowane. Prostokąt podzielony na dwie części: dzień I (trzy piąte) i dzień II (dwie piąte). Zapis: zadania kodowane. Działanie: p = trzy piąte razy jedna druga + dwie piąte razy jedna piąta = dziewiętnaście pięćdziesiątych. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Przebieg omawianego doświadczenia można też przedstawić schematycznie w postaci drzewa. Rozróżnimy dwa etapy: $(1)$ wybór dnia, w którym zadanie zostało rozwiązane, $(2)$ wybór typu zadania rozwiązanego w danym dniu.
Na rysunku poniżej pogrubioną linią zaznaczyliśmy gałęzie odpowiadające wynikom: wylosowano zadanie kodowane rozwiązane pierwszego dnia (na niebiesko), wylosowano zadanie kodowane rozwiązane drugiego dnia (na pomarańczowo).

R12Dhg3RFfbPF1

Rysunek schematu w postaci drzewa, który ilustruje prawdopodobieństwo zdarzenia, że przy losowaniu zadania z zestawu otrzymamy zadanie kodowane. Dwie gałęzie: trzy piąte (dzień I) i dwie piąte (dzień II). Od gałęzi dzień I odchodzą dwie gałęzie : jedna druga (kodowane/ dzień I) i jedna druga (testowe/ dzień I). Od gałęzi dzień II odchodzą dwie gałęzie: jedna piąta (kodowane/ dzień II) i cztery piąte (testowe/ dzień II). — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Na każdej gałęzi zapisaliśmy też, jakie jest prawdopodobieństwo wyboru danej opcji na konkretnym etapie doświadczenia.
Zbierając te informacje, zauważymy zasadę, według której obliczamy szukane prawdopodobieństwo, idąc po każdej z pogrubionych gałęzi. Obliczamy iloczyn prawdopodobieństw zdarzeń z kolejnych etapów, a następnie obliczamy sumę uzyskanych iloczynów:

p = \frac{3}{5} \cdot \frac{1}{2} + \frac{2}{5} \cdot \frac{1}{5}

Stąd

p = \frac{19}{50} .

W kolejnym przykładzie pokażemy, jak umiejętności związane z obliczaniem prawdopodobieństwa można wykorzystać do analizowania informacji, jakimi jesteśmy zasypywani przez media wykorzystywane przez reklamodawców.

Przykład 15

Statystyki pokazują, że w pewnym kraju $1$ osoba na $1000$ jest nosicielem pewnego groźnego wirusa. Firma XMed ogłosiła, że opracowała badanie pozwalające skutecznie rozpoznać nosicielstwo tego wirusa. Przedstawiciele tej firmy przypominają, że nosiciel wirusa może stać się źródłem zakażenia dla osób przebywających w jego otoczeniu i wrażliwych na infekcje, dlatego też wykrywanie oraz leczenie nosicieli wirusów jest społecznie pożądane. Podano przy tym, że po przeprowadzeniu badania opracowanego przez XMed wirus zostanie prawidłowo wykryty u nosiciela w $99,9 %$ przypadków, a w $99 %$ przypadków da się jednoznacznie określić, że badana osoba nie jest nosicielem wirusa.
Ustalimy, czy na podstawie tych danych jesteśmy w stanie ocenić skuteczność badania opracowanego przez XMed.
W tym celu obliczymy najpierw, jakie jest prawdopodobieństwo, że badanie opracowane przez XMed wykryje nosicielstwo.
Załóżmy, że wybieramy losowo obywatela tego kraju. Z treści zadania wynika, że

prawdopodobieństwo zdarzenia, że wylosujemy nosiciela wirusa, jest równe $\frac{1}{1000}$ ,
prawdopodobieństwo zdarzenia, że wylosujemy osobę, która nie jest nosicielem wirusa, jest równe $\frac{999}{1000}$ ,
prawdopodobieństwo tego, że w wyniku badania wirus zostanie wykryty u nosiciela, jest równe $\frac{999}{1000}$ ,
prawdopodobieństwo tego, że w wyniku badania wirus zostanie wykryty u osoby, która nie jest nosicielem, jest równe $\frac{1}{100}$ .

Zapiszmy te prawdopodobieństwa na drzewku.

R1MFEbOg3LfsG1

Rysunek schematu w postaci drzewa, który ilustruje doświadczenie wykrycia nosiciela wirusa. Dwie gałęzie: osoba nie jest nosicielem – dziewięćset dziewięćdziesiąt dziewięć tysięcznych i osoba jest nosicielem – jedna tysięczna. Od gałęzi osoba nie jest nosicielem odchodzą dwie gałęzie: jedna setna – nie jest nosicielem/ badanie pozytywne i dziewięćdziesiąt dziewięć setnych – nie jest nosicielem/ badanie negatywne. Od gałęzi osoba jest nosicielem odchodzą dwie gałęzie: dziewięćset dziewięćdziesiąt dziewięć tysięcznych – nosiciel/ badanie pozytywne i jedna tysięczna – nosiciel/ badanie negatywne. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Wobec tego prawdopodobieństwo p zdarzenia, że badanie wykryje nosicielstwo, jest równe
$p = \frac{1}{1000} \cdot \frac{999}{1000} + \frac{999}{1000} \cdot \frac{1}{100} = \frac{1}{1000} \cdot \frac{999}{1000} + \frac{999}{1000} \cdot \frac{10}{1000} = \frac{999 \cdot (1 + 10)}{1000 \cdot 1000} = \frac{999 \cdot 11}{1000 \cdot 1000} = 0,01098 . . . \approx 0,011$ .
Zatem o nosicielstwie dowiaduje się po badaniu średnio jedenaście osób na tysiąc.
Postawmy się w sytuacji osoby, która po badaniu otrzymała informację, że jest nosicielem wirusa. Ustalimy, na ile ta informacja jest wiarygodna – w tym celu obliczymy, jakie jest prawdopodobieństwo tego, że osoba, która na podstawie badania została uznana za nosiciela, jest rzeczywiście nosicielem wirusa.

Załóżmy, że kraj opisany w treści zadania ma milion mieszkańców. Wtedy na podstawie danych z treści zadania $1000$ z nich to nosiciele wirusa, a $999000$ to osoby, które nie są nosicielami.
W wyniku badania przeprowadzonego przez XMed:
$999$ z $1000$ nosicieli dowie się o tym fakcie (wirus zostanie prawidłowo wykryty u nosiciela w $99,9 %$ przypadków),
$9990$ spośród $999000$ pozostałych osób również zostanie zdiagnozowanych jako nosiciele wirusa (w $99 %$ przypadków da się jednoznacznie określić, że badana osoba nie jest nosicielem wirusa), a przecież żadna z nich nosicielem nie jest.
Dyskwalifikująca dla skuteczności tego badania jest jednak proporcja tych dwóch grup osób, które otrzymały informację o nosicielstwie: jest wśród nich 10 razy więcej osób, które nie są nosicielami wirusa!
Wobec tego prawdopodobieństwo zdarzenia, że osoba, która w wyniku badania firmy XMed dowie się o nosicielstwie jest rzeczywiście nosicielem wirusa, jest równe $\frac{1}{11}$ . To zdecydowanie za mało, żeby uznać to badanie za skuteczne.

iz3aPJUGz3_d5e894

classicmobile

Ćwiczenie 1

W pewnej klasie jest $3$ razy więcej chłopców niż dziewcząt. Losujemy jedną osobę z tej klasy. Prawdopodobieństwo zdarzenia, że wylosujemy dziewczynkę jest równe

RZH3cPO8iUVJw

$\frac{1}{4}$
$\frac{1}{3}$
$\frac{3}{7}$
$\frac{3}{4}$

static

Ćwiczenie 1

W pewnej klasie jest $3$ razy więcej chłopców niż dziewcząt. Losujemy jedną osobę z tej klasy. Prawdopodobieństwo zdarzenia, że wylosujemy dziewczynkę jest równe

RO5keiOaxXT2p

$\frac{1}{4}$
$\frac{1}{3}$
$\frac{3}{7}$
$\frac{3}{4}$

classicmobile

Ćwiczenie 2

Ze zbioru $\{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12\}$ wybieramy losowo jedną liczbę. Oznaczmy przez p prawdopodobieństwo otrzymania liczby podzielnej przez $5$ . Wówczas

Rs334eSf10IKh

$p > \frac{1}{5}$
$p = \frac{1}{5}$
$p = \frac{1}{6}$
$p < \frac{1}{6}$

static

Ćwiczenie 2

Ze zbioru $\{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12\}$ wybieramy losowo jedną liczbę. Oznaczmy przez p prawdopodobieństwo otrzymania liczby podzielnej przez $5$ . Wówczas

RMeOlvfS7RN6f

$p > \frac{1}{5}$
$p = \frac{1}{5}$
$p = \frac{1}{6}$
$p < \frac{1}{6}$

classicmobile

Ćwiczenie 3

Ze zbioru dwucyfrowych liczb naturalnych losujemy jedną liczbę. Prawdopodobieństwo zdarzenia, że będzie to liczba o sumie cyfr równej $16$ , jest równe

R11wlUyGPUJp4

$\frac{16}{90}$
$\frac{1}{16}$
$\frac{3}{89}$
$\frac{1}{30}$

static

Ćwiczenie 3

Ze zbioru dwucyfrowych liczb naturalnych losujemy jedną liczbę. Prawdopodobieństwo zdarzenia, że będzie to liczba o sumie cyfr równej $16$ , jest równe

R1BfmnZOTdtw9

$\frac{16}{90}$
$\frac{1}{16}$
$\frac{3}{89}$
$\frac{1}{30}$

classicmobile

Ćwiczenie 4

Rzucamy dwa razy symetryczną sześcienną kostką do gry. Prawdopodobieństwo zdarzenia, że dwukrotnie otrzymamy liczbę oczek mniejszą od $3$ , jest równe

R1cYwtuMUa2SK

$\frac{1}{18}$
$\frac{1}{9}$
$\frac{2}{9}$
$\frac{2}{3}$

static

Ćwiczenie 4

Rzucamy dwa razy symetryczną sześcienną kostką do gry. Prawdopodobieństwo zdarzenia, że dwukrotnie otrzymamy liczbę oczek mniejszą od $3$ , jest równe

R1bYHALkdxIHk

$\frac{1}{18}$
$\frac{1}{9}$
$\frac{2}{9}$
$\frac{2}{3}$

classicmobile

Ćwiczenie 5

Ze zbioru $\{1, 2, 3, 4, 5, 6, 7, 8\}$ losujemy dwa razy po jednej liczbie ze zwracaniem. Oznaczmy przez $p$ prawdopodobieństwo wylosowania pary liczb, których iloczyn jest podzielny przez $7$ . Wówczas

R1aafe1expLb0

$p = \frac{7}{64}$
$p = \frac{7}{32}$
$p = \frac{15}{64}$
$p = \frac{1}{4}$

static

Ćwiczenie 5

RmgpE6liEsRzC

$p = \frac{7}{64}$
$p = \frac{7}{32}$
$p = \frac{15}{64}$
$p = \frac{1}{4}$

classicmobile

Ćwiczenie 6

Rzucamy $3$ razy symetryczną monetą. Prawdopodobieństwo zajścia zdarzenia, że dokładnie raz wyrzucimy orła, jest równe

RnIrhMSGnrG39

$p = \frac{1}{8}$
$p = \frac{1}{4}$
$p = \frac{1}{3}$
$p = \frac{3}{8}$

static

Ćwiczenie 6

Rzucamy $3$ razy symetryczną monetą. Prawdopodobieństwo zajścia zdarzenia, że dokładnie raz wyrzucimy orła, jest równe

RAIIVwgf6VYSt

$p = \frac{1}{8}$
$p = \frac{1}{4}$
$p = \frac{1}{3}$
$p = \frac{3}{8}$

classicmobile

Ćwiczenie 7

Załóżmy, że w pewnym doświadczeniu losowym dane jest zdarzenie $A$ , ponadto $A’$ jest zdarzeniem przeciwnym do $A$ oraz zachodzi równość $2 \cdot P (A) = 3 \cdot P (A')$ . Stąd prawdopodobieństwo zajścia zdarzenia $A$ jest równe

RfTt0msZU2dtT

$\frac{3}{5}$
$\frac{2}{3}$
$\frac{1}{3}$
$\frac{2}{5}$

static

Ćwiczenie 7

R18d5RuVtqRwT

$\frac{3}{5}$
$\frac{2}{3}$
$\frac{1}{3}$
$\frac{2}{5}$

classicmobile

Ćwiczenie 8

Rzucamy dwa razy symetryczną sześcienną kostką do gry. Prawdopodobieństwo zajścia zdarzenia, że otrzymamy sumę oczek podzielną przez $7$ lub przez $11$ , jest równe

RZs9vLeG3zPTA

$\frac{1}{18}$
$\frac{1}{9}$
$\frac{2}{9}$
$\frac{1}{4}$

static

Ćwiczenie 8

Rzucamy dwa razy symetryczną sześcienną kostką do gry. Prawdopodobieństwo zajścia zdarzenia, że otrzymamy sumę oczek podzielną przez $7$ lub przez $11$ , jest równe

R9lDDfvTbrQyV

$\frac{1}{18}$
$\frac{1}{9}$
$\frac{2}{9}$
$\frac{1}{4}$

classicmobile

Ćwiczenie 9

W każdym z dziewięciu pojemników znajduje się para kul: jedna biała, a druga – czerwona. Z każdego z tych dziewięciu pojemników losujemy jedną kulę. Oznaczmy przez $p$ prawdopodobieństwo zdarzenia, że wśród wylosowanych kul będzie tyle samo czerwonych, co białych. Wówczas

RxG2djsLp0qVM

$p < \frac{1}{5}$
$p = \frac{1}{5}$
$p = \frac{5}{32}$
$p > \frac{5}{32}$

static

Ćwiczenie 9

RvtRPXKN3MYSD

$p < \frac{1}{5}$
$p = \frac{1}{5}$
$p = \frac{5}{32}$
$p > \frac{5}{32}$

classicmobile

Ćwiczenie 10

W pewnej klasie stosunek liczby dziewcząt do liczby chłopców jest równy $7 : 11$ . Losujemy osiem osób z tej klasy. Prawdopodobieństwo tego, że dwie z nich urodziły się w tym samym dniu tygodnia, jest

R1pUxsrligeZ5

mniejsze od $\frac{1}{4}$
równe $\frac{1}{4}$
równe $\frac{1}{2}$
większe od $\frac{1}{2}$

static

Ćwiczenie 10

R6QAENU37Od3h

mniejsze od $\frac{1}{4}$
równe $\frac{1}{4}$
równe $\frac{1}{2}$
większe od $\frac{1}{2}$

iz3aPJUGz3_d5e1374

Ćwiczenie 11

W pudełku znajduje się $17$ kul, ponumerowanych od $1$ do $17$ . Z tego pudełka losujemy jedną kulę. Oblicz prawdopodobieństwo otrzymania:

kuli z numerem podzielnym przez $5$
kuli z nieparzystym numerem dwucyfrowym

$\frac{3}{17}$
$\frac{4}{17}$

Jest $17$ wszystkich możliwych wyników losowania.

Zapisujemy numery kul, które są podzielne przez $5$ : $\{5, 10, 15\}$ . Są więc $3$ takie kule, zatem szukane prawdopodobieństwo jest równe $\frac{3}{17}$ .
Zapisujemy numery kul, które mają numer dwucyfrowy i nieparzysty: $\{11, 13, 15, 17\}$ . Są więc $4$ takie kule, co oznacza, że szukane prawdopodobieństwo jest równe $\frac{4}{17}$ .

Ćwiczenie 12

W pudełku znajduje się $130$ losów, wśród których jest pewna liczba wygrywających. Prawdopodobieństwo zdarzenia, że wybierając z tego pudełka jeden los, wyciągniemy los wygrywający, jest równe $\frac{1}{26}$ . Oblicz, ile jest losów pustych w tym pudełku.

$125$

Oznaczmy przez $n$ liczbę losów wygrywających. Ponieważ prawdopodobieństwo wylosowania losu wygrywającego jest równe $\frac{1}{26}$ , więc wszystkich losów w tej loterii jest $26 n$ . Otrzymujemy więc równanie $26 n = 130$ , stąd $n = 5$ . Oznacza to, że losów pustych jest $130 - 5 = 125$ .

Ćwiczenie 13

Ze zbioru $\{1, 2, 3, . . ., 39, 40\}$ dodatnich liczb całkowitych, które nie są większe od $40$ , wybieramy losowo jedną liczbę. Oblicz prawdopodobieństwo $p$ otrzymania:

liczby mniejszej od $30$
liczby dwucyfrowej.
liczby podzielnej przez $7$
liczby, która nie dzieli się przez $4$

$p = \frac{29}{40}$
$p = \frac{31}{40}$
) $p = \frac{5}{40} = \frac{1}{8}$
$p = \frac{30}{40} = \frac{3}{4}$

W zbiorze $\{1, 2, 3, . . ., 39, 40\}$ jest $40$ liczb.

Zapisujemy zbiór liczb mniejszych od $30$ : ${1, 2, 3, . . ., 29}$ . Jest ich $29$ , zatem $p = \frac{29}{40}$ .
Zapisujemy zbiór liczb dwucyfrowych: ${10, 11, 12, . . ., 40}$ . Jest ich $40 - 9 = 31$ , zatem $p = \frac{31}{40}$ .
Wypisujemy wszystkie liczby podzielne przez $7$ : ${7, 14, 21, 28, 35}$ . Jest ich $5$ , zatem $p = \frac{5}{40} = \frac{1}{8}$ .
Wypisujemy wszystkie liczby podzielne przez $4$ : ${4, 8, 12, 16, 28, 24, 28, 32, 36, 40}$ . Jest ich $10$ , zatem liczb niepodzielnych przez $4$ jest $30$ , stąd $p = \frac{30}{40} = \frac{3}{4}$ . Uwaga. Wśród $4$ kolejnych liczb całkowitych dokładnie jedna jest podzielna przez $4$ . Ponieważ dany zbiór liczb da się podzielić na $10$ rozłącznych podzbiorów tak, że w każdym z tych podzbiorów są $4$ kolejne liczby całkowite, więc szukane prawdopodobieństwo $p$ jest równe $\frac{3}{4}$ .

Ćwiczenie 14

W auli pewnej szkoły wszyscy uczniowie klas trzecich będą pisać próbny egzamin maturalny. Na liście egzaminowanych jest: $36$ uczniów klasy $3 a$ , w tym $16$ dziewczynek, $35$ uczniów klasy $3 b$ , w tym $14$ dziewczynek, $31$ uczniów klasy $3 c$ , w tym $12$ dziewczynek oraz $38$ uczniów klasy $3 d$ , w tym $35$ dziewczynek. Dla każdego ucznia przygotowano jeden stolik, a stoliki ponumerowano kolejnymi liczbami, zaczynając od $1$ . Przed wejściem do auli uczniowie mają losować numer stolika, przy którym będą pisali ten próbny egzamin. Oblicz prawdopodobieństwo zdarzenia, że numer $1$ wylosuje:

osoba z klasy $3 a$
osoba z klasy $3 b$ lub z klasy $3 c$
dziewczynka z klasy $3 d$
chłopiec

$\frac{9}{35}$
$\frac{33}{70}$
$\frac{1}{4}$
$\frac{9}{20}$

Wszystkich egzaminowanych uczniów jest $36 + 35 + 31 + 38 = 140$ .

W klasie $3 a$ jest $36$ osób, więc szukane prawdopodobieństwo jest równe $\frac{36}{140} = \frac{9}{35}$ .
Łącznie w klasach $3 b$ oraz $3 c$ jest $35 + 31 = 66$ uczniów, więc szukane prawdopodobieństwo jest równe $\frac{66}{140} = \frac{33}{70}$ .
W klasie $3 d$ jest $35$ dziewczynek, więc szukane prawdopodobieństwo jest równe $\frac{35}{140} = \frac{1}{4}$ .
Ponieważ dziewczynek jest $16 + 14 + 12 + 35 = 77$ , więc chłopców jest $140 - 77 = 63$ . Zatem szukane prawdopodobieństwo jest równe $\frac{63}{140} = \frac{9}{20}$ .

Ćwiczenie 15

Ze zbioru dwucyfrowych liczb naturalnych wybieramy losowo jedną liczbę. Oblicz prawdopodobieństwo $p$ tego, że

wylosujemy liczbę, której iloczyn cyfr jest równy $24$
wylosujemy liczbę, której suma cyfr jest mniejsza niż $17$
wylosujemy liczbę, której suma cyfr jest parzysta
wylosujemy liczbę, której iloczyn cyfr jest parzysty

$p = \frac{2}{45}$
$p = \frac{29}{30}$
$p = \frac{1}{2}$
$p = \frac{13}{18}$

Jest $90$ wszystkich liczb dwucyfrowych.

Wypisujemy te liczby dwucyfrowe, których iloczyn cyfr jest równy $24 :$ ${38, 46, 64, 83}$ . Zatem są $4$ takie liczby, stąd $p = \frac{4}{90} = \frac{2}{45}$ .
Zauważmy, że $18$ to największa możliwa suma cyfr liczby dwucyfrowej. Wypiszmy więc te liczby dwucyfrowe, których suma cyfr jest równa $17$ lub $18 : {89, 98, 99}$ . Oznacza to, że dla każdej z pozostałych $90 - 3 = 87$ liczb dwucyfrowych suma cyfr jest mniejsza od $17$ , zatem $p = \frac{87}{90} = \frac{29}{30}$ .
Zauważmy, że suma cyfr liczby dwucyfrowej jest parzysta wtedy i tylko wtedy, gdy jej obie cyfry są tej samej parzystości. Liczb dwucyfrowych, które mają obie cyfry parzyste, jest $4 \cdot 5 = 20$ , a liczb dwucyfrowych, które mają obie cyfry nieparzyste, jest $5 \cdot 5 = 25$ . Zatem jest $20 + 25 = 45$ takich liczb, stąd $p = \frac{45}{90} = \frac{1}{2}$ . Uwaga. W każdej dziesiątce liczb dwucyfrowych, które mają ustaloną cyfrę dziesiątek, jest dokładnie $5$ liczb, których cyfra jedności ma tę samą parzystość, co cyfra dziesiątek. Ponieważ zbiór naturalnych liczb dwucyfrowych da się podzielić na $9$ rozłącznych podzbiorów dziesięcioelementowych z ustaloną cyfrą dziesiątek, więc szukane prawdopodobieństwo $p$ jest równe $\frac{5}{10} = \frac{1}{2}$ .
Iloczyn cyfr liczby dwucyfrowej jest nieparzysty wtedy i tylko wtedy, gdy obie cyfry tej liczby są nieparzyste. Takich liczb jest $5 \cdot 5 = 25$ . Zatem dla każdej z pozostałych $90 - 25 = 65$ liczb iloczyn cyfr jest parzysty, więc $p = \frac{65}{90} = \frac{13}{18}$ .

iz3aPJUGz3_d5e1616

Ćwiczenie 16

$100$ uczniów klas trzecich brało udział w balu studniówkowym. Na początku tej imprezy zaplanowane były dwa tańce: polonez i walc. Poloneza zatańczyło $60$ osób, natomiast walca zatańczyło $90$ osób. Wiadomo też, że oba te tańce klasyczne zatańczyły $53$ osoby. Oblicz prawdopodobieństwo $p$ zdarzenia, polegającego na tym, że osoba wybrana losowo spośród uczestników balu nie zatańczyła żadnego z tych dwóch tańców.

$p = \frac{3}{100}$

Sposób $I$
Za zdarzenie elementarne przyjmujemy wynik losowania jednej osoby spośród $100$ uczniów uczestniczących w balu studniówkowym. Oznaczmy:
$A$ – zdarzenie polegające na wylosowaniu osoby, która zatańczyła poloneza,
$B$ – zdarzenie polegające na wylosowaniu osoby, która zatańczyła walca.
Wówczas $|A| = 60$ , $|B| = 90$ , $|A \cap B| = 53$ . Stąd wynika, że liczba osób, które zatańczyły choć jeden z tańców, jest równa $|A \cup B| = |A| + |B| - |A \cap B| = 60 + 90 - 53 = 97$ . Zatem na tym balu były $3$ osoby, które nie zatańczyły żadnego z dwóch tańców klasycznych. Oznacza to, że prawdopodobieństwo p zdarzenia polegającego na tym, że osoba wybrana losowo spośród uczestników balu nie zatańczyła żadnego z tych dwóch tańców, jest równe $p = \frac{3}{100}$ .
Sposób $II$
Rysujemy diagram z uwzględnieniem podziału wszystkich $100$ uczestników na grupy.
RuCLKtZY4eg5I1
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Stwierdzamy na tej podstawie, że wśród uczestników było $7 + 53 + 37 = 97$ osób, które zatańczyły przynajmniej jeden z dwóch tańców klasycznych. Wynika stąd, że $3$ osoby nie zatańczyły żadnego z tych dwóch tańców, stąd $p = \frac{3}{100}$ .

Ćwiczenie 17

W klasie trzeciej jest $35$ uczniów. W każdy piątek, w dodatkowych zajęciach z matematyki bierze udział $30$ z nich, a w każdy wtorek $17$ uczniów tej klasy bierze udział w dodatkowych zajęciach z geografii. Wiadomo też, że $4$ spośród uczniów tej klasy nie bierze udziału w żadnym z tych dwóch dodatkowych rodzajów zajęć. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że osoba wybrana losowo spośród uczniów tej klasy bierze udział zarówno w dodatkowych zajęciach z geografii, jak i z matematyki.

$p = \frac{16}{35}$

Sposób $I$
Za zdarzenie elementarne przyjmujemy wynik losowania jednej osoby spośród 35 uczniów klasy trzeciej. Stąd $|Ω| = 35$ .
Oznaczmy:
$A$ – zdarzenie polegające na wylosowaniu osoby, która uczestniczy w dodatkowych zajęciach z matematyki,
$B$ – zdarzenie polegające na wylosowaniu osoby, która uczestniczy w dodatkowych zajęciach z geografii.
Wówczas $|A| = 30$ , $|B| = 17$ . Ponieważ $4$ uczniów z tej klasy nie bierze udziału ani w zajęciach z matematyki, ani w zajęciach z geografii, więc liczba osób, które biorą udział w choć jednym z tych rodzajów zajęć, jest równa $|A \cup B| = 35 - 4 = 31$ . Zatem liczba uczniów tej klasy, którzy uczęszczają zarówno na dodatkowe zajęcia z matematyki, jak i na dodatkowe zajęcia z geografii, jest równa $|A \cap B| = |A| + |B| - |A \cup B| = 30 + 17 - 31 = 16$ . Wobec tego szukane prawdopodobieństwo jest równe
$P (A \cap B) = \frac{|A \cap B|}{|Ω|} = \frac{16}{35}$ .
Sposób $II$
Oznaczamy przez $n$ liczbę uczniów, którzy biorą udział w obydwu rodzajach zajęć. Rysujemy diagram z uwzględnieniem podziału wszystkich $35$ uczestników na grupy.
RPkNcY6BkVbAu1
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Stwierdzamy na tej podstawie, że $30 - n + n + 17 - n + 4 = 35$ , stąd $n = 16$ . Zatem szukane prawdopodobieństwo jest równe $\frac{16}{35}$ .

Ćwiczenie 18

W pewnym doświadczeniu losowym dane jest zdarzenie $A$ , natomiast $A’$ jest zdarzeniem przeciwnym do $A$ . Oblicz prawdopodobieństwo zdarzenia $A$ , wiedząc, że

$P (A) = 4 \cdot P (A')$
$2 \cdot P (A') = 7 \cdot P (A)$
$P (A) = P (A') + \frac{3}{17}$
$3 \cdot P (A) + 7 \cdot P (A') = 5 \frac{2}{5}$

$P (A) = \frac{4}{5}$
$P (A) = \frac{2}{9}$
$P (A) = \frac{10}{17}$
$P (A) = \frac{2}{5}$

Ponieważ $P (A') = 1 - P (A)$ , więc $P (A) = 4 \cdot P (A') = 4 \cdot (1 - P (A)) = 4 - 4 \cdot P (A)$ , stąd $P (A) = \frac{4}{5}$ .
Ponieważ $P (A') = 1 - P (A)$ , więc $2 \cdot P (A') = 2 \cdot (1 - P (A)) = 7 \cdot P (A)$ , stąd $P (A) = \frac{2}{9}$ .
Ponieważ $P (A') = 1 - P (A)$ , więc $P (A) = P (A') + \frac{3}{17} = 1 - P (A) + \frac{3}{17}$ , stąd $P (A) = \frac{10}{17}$ .
Ponieważ $P (A) + P (A') = 1$ , więc $3 \cdot P (A) + 7 \cdot P (A') = 7 \cdot (P (A) + P (A')) - 4 \cdot P (A) = 7 - 4 \cdot P (A) = 5 \frac{2}{5}$ , stąd $4 \cdot P (A) = 1 \frac{3}{5}$ , czyli $P (A) = \frac{2}{5}$ .

Ćwiczenie 19

W pewnym doświadczeniu losowym $A$ i $B$ są zdarzeniami, $A’$ jest zdarzeniem przeciwnym do $A, B’$ jest zdarzeniem przeciwnym do $B$ .

Oblicz $P (A \cup B)$ , wiedząc, że zdarzenia $A$ i $B$ są rozłączne oraz $P (A') = \frac{3}{4}$ , $P (B') = 0,61$ .
Oblicz $P (A \cap B)$ , wiedząc, że $P (A \cup B) = \frac{2}{3}$ , $P (A') = \frac{1}{2}$ , $P (B') = \frac{3}{4}$ .

$P (A \cup B) = 0,64$
$P (A \cap B) = \frac{1}{12}$

Ponieważ zbiory $A$ i $B$ są rozłączne, więc $P (A \cup B) = P (A) + P (B)$ . Obliczamy: $P (A) = 1 - P (A') = \frac{1}{4}$ , $P (B) = 1 - P (B') = 0,39$ , stąd $P (A \cup B) = P (A) + P (B) = \frac{1}{4} + 0,39 = 0,64$ .
Obliczamy: $P (A) = 1 - P (A') = \frac{1}{2}$ , $P (B) = 1 - P (B') = \frac{1}{4}$ . Ponieważ $P (A \cup B) = P (A) + P (B) - P (A \cap B)$ , więc $P (A \cap B) = P (A) + P (B) - P (A \cup B) = \frac{1}{2} + \frac{1}{4} - \frac{2}{3} = \frac{1}{12}$ .

Ćwiczenie 20

W kopercie znajduje się $10$ kartek, ponumerowanych od $1$ do $10$ . Z tej koperty losujemy dwa razy po jednej kartce ze zwracaniem. Oblicz prawdopodobieństwo otrzymania:

dwóch kartek o różnych numerach,
takich dwóch kartek, że iloraz numeru na pierwszej kartce przez numer na drugiej kartce jest liczbą całkowitą.

$\frac{9}{10}$
$\frac{27}{100}$

Sposób $I$ (schemat klasyczny). W tym doświadczeniu jest $10 \cdot 10 = 100$ wszystkich zdarzeń elementarnych.

Zliczanie liczby zdarzeń elementarnych sprzyjających przeprowadzimy na dwa sposoby.
Sposób $I$
Ponieważ kartka wylosowana za drugim razem musi mieć inny numer od tej, która została wylosowana za pierwszym razem, więc różne numery wylosowanych kartek można otrzymać na $10 \cdot 9 = 90$ sposobów.
Sposób $II$
Jest $10$ sposobów wylosowania dwa razy tej samej kartki, więc mamy $100 - 10 = 90$ możliwości wylosowania pary kartek o różnych numerach. Zatem szukane prawdopodobieństwo jest równe $\frac{90}{100} = \frac{9}{10}$ . Uwaga. Niezależnie od tego, jaki numer ma kartka wylosowana za pierwszym razem, kartka wylosowana za drugim razem ma w jednym przypadku ten sam numer, a w pozostałych dziewięciu przypadkach jej numer różni się od tego na pierwszej kartce. Oznacza to, że szukane prawdopodobieństwo jest równe $\frac{9}{10}$ .
Zauważmy, że jeżeli numer na pierwszej kartce jest podzielny przez numer na drugiej kartce, to możemy otrzymać iloraz równy

$1$ (jest $10$ takich możliwości),
$2$ (jest $5$ takich możliwości),
$3$ (są $3$ takie możliwości),
$4$ lub $5$ (za każdym razem są $2$ możliwości),
$6, 7, 8, 9$ lub $10$ (za każdym razem jest $1$ taka możliwość).

Zatem wszystkich zdarzeń sprzyjających jest $10 + 5 + 3 + 2 \cdot 2 + 5 \cdot 1 = 27$ , więc szukane prawdopodobieństwo jest równe $\frac{27}{100}$ . Uwaga. Łączną liczbę wielokrotności każdego z elementów danego zbioru można obliczyć, używając symbolu części całkowitej: $⌊\frac{10}{1}⌋ + ⌊\frac{10}{2}⌋ + ⌊\frac{10}{3}⌋ + ⌊\frac{10}{4}⌋ + ⌊\frac{10}{5}⌋ + ⌊\frac{10}{6}⌋ + ⌊\frac{10}{7}⌋ + ⌊\frac{10}{8}⌋ + ⌊\frac{10}{9}⌋ + ⌊\frac{10}{10}⌋ .$
Sposób $II$
Rysujemy drzewo z uwzględnieniem wszystkich gałęzi, które prowadzą do sytuacji sprzyjającej danemu zdarzeniu. Na tej podstawie obliczamy szukane prawdopodobieństwa.
Sposób $III$
Rysujemy tabelę $10 x 10$ i dla każdego z podpunktów zaznaczamy w niej pola odpowiadające zdarzeniom elementarnym sprzyjającym konkretnemu zdarzeniu. Na tej podstawie obliczamy szukane prawdopodobieństwa.

Ćwiczenie 21

Rzucamy dwa razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo $p$ zdarzenia, że

największa wyrzucona liczba oczek jest równa $1$ lub $2$ , lub $3$ .
największa wyrzucona liczba oczek jest równa $5$ .

$p = \frac{1}{4}$
$p = \frac{1}{4}$

Sposób $I$ (schemat klasyczny).
W tym doświadczeniu jest $6 \cdot 6 = 36$ wszystkich zdarzeń elementarnych.

Największa wyrzucona liczba oczek nie jest większa od $3$ , gdy w obu rzutach wypadnie liczba oczek nie większa od $3$ . Mamy więc $3 \cdot 3 = 9$ zdarzeń elementarnych sprzyjających, więc $p = \frac{9}{36} = \frac{1}{4}$ .
Rozumując podobnie jak w rozwiązaniu podpunktu $a)$ , stwierdzamy, że
jest $5 \cdot 5 = 25$ zdarzeń elementarnych sprzyjających zdarzeniu, że największa wyrzucona liczba oczek jest równa $1, 2, 3, 4$ lub $5$ ,
jest $4 \cdot 4 = 16$ zdarzeń elementarnych sprzyjających zdarzeniu, że największa wyrzucona liczba oczek jest równa $1, 2, 3$ lub $4$ .
Oznacza to, że jest $5^{2} - 4^{2} = 9$ zdarzeń elementarnych sprzyjających zdarzeniu, że największa wyrzucona liczba oczek jest równa $5$ . Stąd $p = \frac{9}{36} = \frac{1}{4}$ .

Sposób $II$
Rysujemy tabelę $6 x 6$ i dla każdego z podpunktów zaznaczamy w niej pola odpowiadające zdarzeniom elementarnym sprzyjającym konkretnemu zdarzeniu. Na tej podstawie obliczamy szukane prawdopodobieństwa.
Sposób $III$
Rysujemy drzewo z uwzględnieniem wszystkich gałęzi, które prowadzą do sytuacji sprzyjającej danemu zdarzeniu. Na tej podstawie obliczamy szukane prawdopodobieństwa.

iz3aPJUGz3_d5e1893

Ćwiczenie 22

Losujemy dwa wierzchołki spośród wszystkich wierzchołków siedmiokąta foremnego. Oblicz prawdopodobieństwo zdarzenia, że wylosujemy w ten sposób końce pewnej przekątnej tego wielokąta.

$\frac{2}{3}$

Za zdarzenie elementarne przyjmujemy wynik jednoczesnego losowania dwóch wierzchołków spośród siedmiu. Zatem każde zdarzenie elementarne to dwuelementowy podzbiór zbioru siedmioelementowego, więc wszystkich zdarzeń elementarnych jest $\frac{7 \cdot 6}{2} = 21$ . Ponieważ ten wielokąt ma $\frac{7 \cdot (7 - 3)}{2} = 14$ przekątnych, więc szukane prawdopodobieństwo jest równe $\frac{14}{21} = \frac{2}{3}$ .
Uwaga. Wybrany wierzchołek siedmiokąta foremnego można połączyć sześcioma odcinkami z każdym z pozostałych wierzchołków tego siedmiokąta. Wśród tych sześciu odcinków: dwa to boki siedmiokąta, a cztery to jego przekątne. Zatem szukane prawdopodobieństwo jest równe $\frac{4}{6} = \frac{2}{3}$ .

Ćwiczenie 23

Ze zbioru liczb $\{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11\}$ losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo:

zdarzenia $A$ , polegającego na wylosowaniu dwóch liczb, z których pierwsza jest o $2$ lub o $3$ mniejsza od drugiej.
zdarzenia $B$ , polegającego na wylosowaniu dwóch liczb, których iloczyn jest podzielny przez $10$ .
zdarzenia $C$ , polegającego na wylosowaniu dwóch liczb, których suma jest podzielna przez $7$ .
zdarzenia $D$ , polegającego na wylosowaniu dwóch liczb, których suma kwadratów jest podzielna przez $3$ .

$P (A) = \frac{17}{121}$
$P (B) = \frac{29}{121}$
$P (C) = \frac{17}{121}$
$P (D) = \frac{9}{121}$

Sposób $I$
(schemat klasyczny). Za zdarzenie elementarne w takim doświadczeniu przyjmujemy wynik dwukrotnego losowania jednej liczby ze zbioru jedenastoelementowego ze zwracaniem. Każde zdarzenie elementarne możemy więc zapisać jako dwuelementowy ciąg $(a, b)$ , gdzie $a, b$ są elementami ze zbioru $\{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11\}$ . Oznaczmy przez $Ω$ zbiór zdarzeń elementarnych. Wszystkich zdarzeń elementarnych jest więc $|Ω| = 1 1^{2} = 121$ .

Oznaczmy pierwszą wylosowaną liczbę przez $n$ i zauważmy, że jeśli $n = 1, 2, . . ., 8$ , to zdarzenia elementarne $(n, n + 2)$ oraz $(n, n + 3)$ sprzyjają zdarzeniu $A$ . W pozostałych przypadkach jest tylko jedno sprzyjające zdarzenie elementarne: $(9, 11)$ . Wobec tego $|A| = 8 \cdot 2 + 1 = 17$ , stąd na mocy definicji klasycznej otrzymujemy $P (A) = \frac{17}{121}$ .
Zliczanie zdarzeń elementarnych sprzyjających zdarzeniu $B$ podzielimy na następujące rozłączne przypadki:
$-$ jeżeli pierwszą wylosowaną liczbą będzie $1, 3, 7, 9$ lub $11$ , to drugą wylosowaną liczbą musi być $10$ – łącznie jest więc w tym przypadku $5$ zdarzeń elementarnych sprzyjających B,
$-$ jeżeli pierwszą wylosowaną liczbą będzie $2, 4, 6$ lub $8$ , to drugą wylosowaną liczbą musi być $5$ lub $10$ – łącznie jest więc w tym przypadku $4 \cdot 2 = 8$ zdarzeń elementarnych sprzyjających $B,$
$-$ jeżeli pierwszą wylosowaną liczbą będzie $5$ , to drugą wylosowaną liczbą musi być $2, 4, 6, 8$ , lub $10$ – łącznie jest więc w tym przypadku $5$ zdarzeń elementarnych sprzyjających $B$ ,
$-$ jeżeli pierwszą wylosowaną liczbą będzie $10$ , to druga wylosowana liczba może być dowolna – łącznie jest więc w tym przypadku $11$ zdarzeń elementarnych sprzyjających $B$ .
Wobec tego $|B| = 5 + 8 + 5 + 11 = 29$ , stąd na mocy definicji klasycznej otrzymujemy $P (B) = \frac{29}{121}$ .
Zliczanie zdarzeń elementarnych sprzyjających zdarzeniu $C$ podzielimy na trzy rozłączne przypadki:
$-$ suma wylosowanych liczb jest równa $7$ – w tym przypadku jest $6$ zdarzeń elementarnych sprzyjających $C$ ,
$-$ suma wylosowanych liczb jest równa $14$ – w tym przypadku jest $9$ zdarzeń elementarnych sprzyjających $C$ ,
$-$ suma wylosowanych liczb jest równa $21$ – w tym przypadku są $2$ zdarzenia elementarne sprzyjające $C$ .
Wobec tego $|C| = 6 + 9 + 2 = 17$ , stąd na mocy definicji klasycznej otrzymujemy $P (C) = \frac{17}{121}$ .
Ponieważ reszta z dzielenia przez $3$ kwadratu każdej liczby całkowitej niepodzielnej przez $3$ jest równa $1$ , więc suma kwadratów dwóch liczb całkowitych jest podzielna przez $3$ wtedy i tylko wtedy, gdy obie te liczby dzielą się przez $3$ . W zbiorze $\{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11\}$ są dokładnie trzy liczby podzielne przez $3 : 3, 6$ oraz $9$ . Wobec tego zdarzeń elementarnych sprzyjających D jest $|D| = 3 \cdot 3 = 9$ , stąd na mocy definicji klasycznej otrzymujemy $P (D) = \frac{9}{121}$ .

Sposób $II$
Rysujemy drzewo z uwzględnieniem wszystkich gałęzi, które prowadzą do sytuacji sprzyjającej danemu zdarzeniu. Na tej podstawie obliczamy szukane prawdopodobieństwa.
Sposób $III$
Rysujemy tabelę $11 x 11$ i dla każdego z podpunktów zaznaczamy w niej pola odpowiadające zdarzeniom elementarnym sprzyjającym konkretnemu zdarzeniu. Na tej podstawie obliczamy szukane prawdopodobieństwa.

Ćwiczenie 24

Rzucamy dwa razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo takiego zdarzenia $A$ , że w pierwszym rzucie wypadnie liczba oczek większa niż w drugim i iloczyn liczb wyrzuconych oczek będzie podzielny przez $4$ .

$P (A) = \frac{1}{6}$

Sposób $I$
(schemat klasyczny). Za zdarzenie elementarne w takim doświadczeniu przyjmujemy wynik dwukrotnego rzutu kostką sześcienną. Zbiór zdarzeń elementarnych $Ω$ jest zatem zbiorem par $(a, b)$ takich, że a, b są elementami ze zbioru $\{1, 2, 3, 4, 5, 6\}$ . Wszystkich zdarzeń elementarnych jest więc $|Ω| = 6^{2} = 36$ . Wypisujemy zdarzenia elementarne, które sprzyjają zdarzeniu $A$ : $(4, 1)$ , $(4, 2)$ , $(4, 3)$ , $(5, 4)$ , $(6, 2)$ , $(6, 4)$ . Oznacza to, że $|A| = 6$ , stąd $P (A) = \frac{6}{36} = \frac{1}{6}$ .
Sposób $II$
Rysujemy tabelę $6 x 6$ i zaznaczamy w niej pola odpowiadające zdarzeniom elementarnym sprzyjającym zdarzeniu $A$ . Na tej podstawie obliczamy szukane prawdopodobieństwo.
Sposób $III$
Rysujemy drzewo z uwzględnieniem wszystkich gałęzi, które prowadzą do sytuacji sprzyjającej danemu zdarzeniu. Na tej podstawie obliczamy szukane prawdopodobieństwo.

Ćwiczenie 25

Z pojemnika, w którym jest $20$ losów: $3$ wygrywające oraz $17$ pustych, losujemy dwa razy po jednym losie bez zwracania. Oblicz prawdopodobieństwo p zdarzenia, że oba wylosowane losy będą wygrywające.

$p = \frac{3}{190}$

Sposób $I$
(schemat klasyczny). Za zdarzenie elementarne w takim doświadczeniu przyjmujemy wynik dwukrotnego losowania ze zbioru dwudziestu losów bez zwracania. Oznaczmy przez $w_{1}, w_{2}, w_{3}$ losy wygrywające, a przez $p_{1}, p_{2}, p_{3}, . . ., p_{17}$ – losy puste. Każde zdarzenie elementarne możemy zapisać jako dwuelementowy ciąg $(a, b)$ , gdzie a, b są różnymi elementami z dwudziestoelementowego zbioru $\{w_{1}, w_{2}, w_{3}, p_{1}, p_{2}, p_{3}, . . ., p_{17}\}$ . Wszystkich zdarzeń elementarnych jest więc $20 \cdot 19 = 380$ . Zdarzeniu, że oba wylosowane losy będą wygrywające sprzyja $3 \cdot 2 = 6$ następujących zdarzeń elementarnych: $(w_{1}, w_{2})$ , $(w_{1}, w_{3})$ , $(w_{2}, w_{1})$ , $(w_{2}, w_{3})$ , $(w_{3}, w_{1})$ , $(w_{3}, w_{2})$ . Stąd $p = \frac{6}{380} = \frac{3}{190}$ .
Sposób $II$
Rysujemy drzewo z uwzględnieniem wszystkich gałęzi, które prowadzą do sytuacji sprzyjającej danemu zdarzeniu. Na tej podstawie obliczamy szukane prawdopodobieństwo.
Sposób $III$
Rysujemy tabelę $20 x 20$ . Ponieważ losujemy bez zwracania, więc odrzucamy z tabeli $20$ pól leżących na przekątnej. Z pozostałych $380$ pól wybieramy te, które odpowiadają zdarzeniom elementarnym sprzyjającym danemu zdarzeniu. Na tej podstawie obliczamy szukane prawdopodobieństwo.

Uwaga. W tym doświadczeniu za zdarzenie elementarne możemy przyjąć dwuelementowy podzbiór $\{a, b\}$ dwudziestoelementowego zbioru $\{w_{1}, w_{2}, w_{3}, p_{1}, p_{2}, p_{3}, . . ., p_{17}\}$ . Wszystkich zdarzeń elementarnych jest wtedy $\frac{19 \cdot 20}{2} = 190$ . Zdarzeniu, że oba wylosowane losy będą wygrywające sprzyjają następujące $3$ zdarzenia elementarne: $\{w_{1}, w_{2}\}$ , $\{w_{1}, w_{3}\}$ , $\{w_{2}, w_{3}\}$ . Stąd $p = \frac{3}{190}$ .

Ćwiczenie 26

W kopercie jest $15$ kartek ponumerowanych liczbami od $1$ do $15$ . Z tej koperty losujemy jednocześnie dwie kartki. Oblicz prawdopodobieństwo zdarzenia:

$A$ – iloczyn liczb na wylosowanych kartkach jest nieparzysty,
$B$ – suma liczb na wylosowanych kartkach jest nieparzysta.

$P (A) = \frac{4}{15}$
$P (B) = \frac{8}{15}$

Sposób $I$
Za zdarzenie elementarne w takim doświadczeniu przyjmujemy wynik jednoczesnego losowania dwóch kartek spośród piętnastu. Zatem każde zdarzenie elementarne to dwuelementowy podzbiór $\{a, b\}$ piętnastoelementowego zbioru $\{1, 2, 3, . . ., 15\}$ . Wszystkich zdarzeń elementarnych jest więc $|Ω| = \frac{15 \cdot 14}{2} = 105$ .

W przypadku zdarzenia A każda z dwóch wylosowanych kartek musi mieć numer nieparzysty, a kartek z numerem nieparzystym jest $8$ . Zatem zdarzeniu A sprzyja $|A| = \frac{8 \cdot 7}{2} = 28$ zdarzeń elementarnych, stąd $P (A) = \frac{28}{105} = \frac{4}{15}$ .
W przypadku $B$ jedna z wylosowanych kartek musi mieć numer nieparzysty, a druga – parzysty. Ponieważ kartek z numerem nieparzystym jest $8$ , a z numerem parzystym – $7$ , więc zdarzeniu $B$ sprzyja $|B| = 8 \cdot 7 = 56$ zdarzeń elementarnych. Oznacza to, że $P (B) = \frac{56}{105} = \frac{8}{15}$ .
Uwaga. Mimo, że w treści zadania jest mowa o jednoczesnym losowaniu dwóch kartek, to jednak za zdarzenie elementarne w tym doświadczeniu można przyjąć dwuelementowy ciąg $(a, b)$ , gdzie $a, b \in \{1, 2, 3, . . ., 15\}$ oraz $a \neq b$ . Narzucona w ten sposób kolejność wylosowanych kartek nie ma wpływu ani na sumę, ani na iloczyn liczb na wylosowanych kartkach, ponieważ te działania są przemienne. Tym sposobem wszystkich zdarzeń elementarnych jest tyle, ile dwuelementowych ciągów ze zbioru $\{1, 2, 3, . . ., 15\}$ bez powtórzeń, stąd $|Ω| = 15 \cdot 14 = 210$ . Wówczas:

zdarzeń elementarnych sprzyjających zdarzeniu $A$ jest tyle, ile dwuelementowych ciągów ze zbioru $\{1, 3, 5, 7, 9, 11, 13, 15\}$ bez powtórzeń, stąd $|A| = 8 \cdot 7 = 56$ , co oznacza, że $P (A) = \frac{56}{210} = \frac{4}{15}$ .
zdarzeniu $B$ sprzyja każde zdarzenie elementarne, w którym wylosowane liczby są różnej parzystości. Zatem możliwe są dwa rozłączne przypadki:
$-$ pierwsza wylosowana liczba jest parzysta i druga - jest nieparzysta
$-$ pierwsza wylosowana liczba jest nieparzysta i druga - jest parzysta.
Wobec tego $|A| = 7 \cdot 8 + 8 \cdot 7 = 112$ , stąd $P (B) = \frac{112}{210} = \frac{8}{15}$ .
Mając powyższe na uwadze, można przebieg analizowanego doświadczenia zilustrować za pomocą:
$-$ drzewa, uwzględniając wszystkie gałęzie, które prowadzą do sytuacji sprzyjającej danemu zdarzeniu,
$-$ tabeli $15$ na $15$ , w której odrzucamy $15$ pól leżących na przekątnej. Z pozostałych $210$ pól wybieramy te, które odpowiadają zdarzeniom elementarnym sprzyjającym danemu zdarzeniu.
Na tej podstawie obliczamy szukane prawdopodobieństwo.

Ćwiczenie 27

W klasie jest $35$ uczniów, przy czym chłopców jest o $3$ mniej niż dziewczynek. Losujemy dwie osoby z tej klasy. Oblicz prawdopodobieństwo zdarzenia, że wśród wylosowanych osób będzie co najmniej jedna dziewczynka.

$\frac{95}{119}$

Za zdarzenie elementarne przyjmujemy wynik losowania $2$ osób spośród $35$ . Zatem każde zdarzenie elementarne to dwuelementowy podzbiór ze zbioru $35$ uczniów tej klasy. Wszystkich zdarzeń elementarnych jest więc $|Ω| = \frac{35 \cdot 34}{2} = 595$ . Obliczamy, że w tej klasie jest $16$ chłopców i $19$ dziewczynek. Rozpatrzmy zdarzenie $A$ polegające na tym, że wśród wylosowanych osób będzie co najmniej jedna dziewczynka. Wtedy zdarzeniem przeciwnym do $A$ jest takie zdarzenie $A’$ , że wśród wylosowanych osób nie będzie żadnej dziewczynki. To oznacza, że $|A '| = \frac{16 \cdot 15}{2} = 120$ , a więc $P (A ') = \frac{120}{595} = \frac{24}{119}$ . Stąd $P (A) = 1 - P (A ') = 1 - \frac{24}{119} = \frac{95}{119}$ .

iz3aPJUGz3_d5e2127

Ćwiczenie 28

W talii $52$ kart do brydża jest po $13$ kart w każdym z czterech kolorów: trefl, karo, kier, pik. W każdym kolorze jest jeden as, a także trzy figury: król, dama, walet oraz $9$ kart numerowanych od $2$ do $10$ . Z takiej talii $52$ kart losujemy dwa razy po jednej karcie bez zwracania. Oblicz prawdopodobieństwo p zdarzenia, że obie wylosowane karty będą figurami. Zapisz wynik w postaci ułamka nieskracalnego.

$p = \frac{11}{221}$

Sposób $I$ (schemat klasyczny).
Za zdarzenie elementarne w takim doświadczeniu przyjmujemy wynik dwukrotnego losowania ze zbioru $52$ kart bez zwracania. Każde zdarzenie elementarne możemy zapisać jako dwuelementowy ciąg $(a, b)$ , gdzie $a, b$ są różnymi elementami ze zbioru $52$ kart. Wszystkich zdarzeń elementarnych jest więc $52 \cdot 51 = 2652$ . Wśród $52$ kart w tej talii jest $4 \cdot 3 = 12$ figur. Zatem zdarzeniu, że obie wylosowane karty będą figurami, sprzyjają $12 \cdot 11 = 132$ zdarzenia elementarne. Stąd $p = \frac{132}{2652} = \frac{11}{221}$ .
Sposób $II$
Rysujemy drzewo z uwzględnieniem wszystkich gałęzi, które prowadzą do sytuacji sprzyjającej danemu zdarzeniu. Na tej podstawie obliczamy szukane prawdopodobieństwo.
Uwaga. W tym doświadczeniu za zdarzenie elementarne możemy przyjąć dwuelementowy podzbiór $\{a, b\}$ zbioru 52 kart. Wszystkich zdarzeń elementarnych jest wtedy $\frac{52 \cdot 51}{2} = 1326$ . Zdarzeniu, że obie wylosowane karty będą figurami, sprzyja wówczas $\frac{12 \cdot 11}{2} = 66$ zdarzeń elementarnych. Stąd $p = \frac{66}{1326} = \frac{11}{221}$ .

Ćwiczenie 29

W pudełku znajdują się kule, przy czym co dziesiąta z nich jest biała, a każda z pozostałych ma kolor czerwony lub kolor zielony. Przy losowaniu jednej kuli z tego pudełka prawdopodobieństwo wylosowania kuli czerwonej lub zielonej jest trzy razy większe niż prawdopodobieństwo wylosowania kuli czerwonej lub białej. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że przy losowaniu jednej kuli z tego pudełka wylosujemy kulę zieloną.

$\frac{7}{10}$

Rozpatrzmy doświadczenie polegające na losowaniu jednej kuli z tego pudełka. Oznaczmy:

$B$ – zdarzenie, że wylosowano kulę białą,
$C$ – zdarzenie, że wylosowano kulę czerwoną,
$Z$ – zdarzenie, że wylosowano kulę zieloną.

Zdarzenia $B, C$ oraz $Z$ są parami rozłączne, a zdarzenie, że zajdzie $B$ lub $C$ , lub $Z$ jest pewne, stąd $P (B \cup C \cup Z) = 1$
Z treści zadania wynika, że $P (B) = \frac{1}{10}$ oraz $P (C \cup Z) = 3 \cdot P (B \cup C)$ . Wynika stąd, że $P (C \cup Z) = 1 - P (B) = \frac{9}{10}$ , co oznacza, że $P (B \cup C) = \frac{1}{3} \cdot P (C \cup Z) = \frac{1}{3} \cdot \frac{9}{10} = \frac{3}{10}$ . Ponieważ $P (B \cup C) = P (B) + P (C)$ , więc $P (C) = \frac{3}{10} - \frac{1}{10} = \frac{2}{10}$ . Wobec tego $P (Z) = P (C \cup Z) - P (C) = \frac{9}{10} - \frac{2}{10} = \frac{7}{10}$ .

Ćwiczenie 30

Rzucamy trzy razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia $A$ – dokładnie raz wypadnie szóstka.

$P (A) = \frac{25}{72}$

Każde zdarzenie elementarne możemy zapisać jako trzyelementowy ciąg $(a, b, c)$ , gdzie $a, b, c$ są liczbami ze zbioru ${1, 2, 3, 4, 5, 6}$ wyników rzutu kostką sześcienną. Wszystkich zdarzeń elementarnych jest więc $|Ω| = 6^{3} = 216$ . Zliczanie zdarzeń elementarnych sprzyjających $A$ rozkładamy na dwa etapy:

obliczamy, na ile sposobów można wybrać rzut, w którym wypadła szóstka: wybieramy jeden rzut z $3$ , więc można to zrobić na $3$ sposoby,
obliczamy, ile jest wyników pozostałych rzutów: w każdym z pozostałych dwóch rzutów mamy do wyboru jeden z pięciu wyników: $1, 2, 3, 4$ lub $5$ , zatem jest $5 \cdot 5 = 25$ takich możliwości.

Wobec tego $|A| = 3 \cdot 5^{2} = 75$ . Stąd $P (A) = \frac{75}{216} = \frac{25}{72}$ .

Ćwiczenie 31

W kopercie jest $5$ kartek ponumerowanych liczbami naturalnymi od $1$ do $5$ . Losujemy z tej koperty po kolei $5$ kartek, a wyniki kolejnych losowań notujemy jeden za drugim, zapisując w ten sposób liczbę pięciocyfrową. Oblicz prawdopodobieństwo, że w wyniku takiego postępowania zapiszemy liczbę, w której:

suma każdych dwóch sąsiednich cyfr będzie nieparzysta,
cyfry $1$ oraz $2$ będą zapisane na sąsiednich miejscach.

$\frac{1}{10}$
$\frac{2}{5}$

Każde zdarzenie elementarne to pięcioelementowy ciąg bez powtórzeń $(a, b, c, d, e)$ , gdzie $a, b, c, d, e$ są liczbami ze zbioru ${1, 2, 3, 4, 5}$ . Wszystkich zdarzeń elementarnych jest więc $|Ω| = 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 120$ .

Oznaczmy: $A$ – zdarzenie, że otrzymaliśmy liczbę pięciocyfrową, w której suma każdych dwóch sąsiednich cyfr jest nieparzysta. W tym przypadku kolejne pary elementów ciągu $(a, b, c, d, e)$ muszą być liczbami różnej parzystości. Jest to możliwe wtedy i tylko wtedy, gdy $a, c$ oraz $e$ będą liczbami wybranymi bez powtórzeń ze zbioru ${1, 3, 5}$ , natomiast $b$ oraz $d$ będą różnymi liczbami ze zbioru ${2, 4}$ .
Wobec tego $|A| = (3 \cdot 2 \cdot 1) \cdot (2 \cdot 1) = 12$ , stąd $P (A) = \frac{12}{120} = \frac{1}{10}$ .
Oznaczmy: $B$ – zdarzenie, że otrzymaliśmy liczbę pięciocyfrową, w której cyfry $1$ oraz $2$ są zapisane na sąsiednich miejscach. W rozpatrywanych ciągach $(a, b, c, d, e)$ cyfry $1, 2$ można wtedy zapisać na $4$ sposoby: jako $a, b$ lub jako $b, c$ , lub jako $c, d$ , lub jako $d, e$ . W każdym z tych przypadków cyfry $1, 2$ rozmieszczamy na przydzielonych im miejscach na $2$ sposoby, a pozostałe trzy cyfry rozmieszczamy na trzech pozostałych miejscach na $3 \cdot 2 \cdot 1 = 6$ sposobów. Zatem $|B| = 4 \cdot 2 \cdot 6 = 48$ , stąd $P (B) = \frac{48}{120} = \frac{2}{5}$ .

Ćwiczenie 32

Rzucamy trzy razy symetryczną sześcienną kostką do gry. Rozstrzygnij, które zdarzenie jest wtedy bardziej prawdopodobne: $A$ – wypadła suma oczek równa $11$ czy $B$ – wypadła suma oczek równa $12$ .

Uwaga. W literaturze to zadanie jest znane jako paradoks/problem kawalera de’Mere.
$P (A) = \frac{27}{216} > P (B) = \frac{25}{216}$

wypadła jedna jedynka, jedna czwórka oraz jedna szóstka – jest $3 \cdot 2 \cdot 1 = 6$ takich zdarzeń elementarnych,
wypadła jedna jedynka oraz dwie piątki – są $3$ takie zdarzenia elementarne,
wypadła jedna dwójka, jedna trójka oraz jedna szóstka – jest $3 \cdot 2 \cdot 1 = 6$ takich zdarzeń elementarnych,
wypadła jedna dwójka, jedna czwórka oraz jedna piątka – jest $3 \cdot 2 \cdot 1 = 6$ takich zdarzeń elementarnych,
wypadły dwie trójki oraz jedna piątka – są $3$ takie zdarzenia elementarne,
wypadła jedna trójka oraz dwie czwórki – są $3$ takie zdarzenia elementarne.

Wobec tego $|A| = 6 + 3 + 6 + 6 + 3 + 3 = 27$ , stąd $P (A) = \frac{27}{216}$ .
Sumę $12$ możemy otrzymać na $6$ sposobów:

wypadła jedna jedynka, jedna piątka oraz jedna szóstka – jest $3 \cdot 2 \cdot 1 = 6$ takich zdarzeń elementarnych,
wypadła jedna dwójka, jedna czwórka oraz jedna szóstka – jest $3 \cdot 2 \cdot 1 = 6$ takich zdarzeń elementarnych,
wypadła jedna dwójka oraz dwie piątki – są $3$ takie zdarzenia elementarne,
wypadły dwie trójki oraz jedna szóstka – są $3$ takie zdarzenia elementarne,
wypadła jedna trójka, jedna czwórka oraz jedna piątka – jest $3 \cdot 2 \cdot 1 = 6$ takich zdarzeń elementarnych,
wypadły trzy czwórki – jest $1$ takie zdarzenie elementarne.

Wobec tego $|B| = 6 + 6 + 3 + 3 + 6 + 1 = 25$ , stąd $P (B) = \frac{25}{216}$ .
Oznacza to, że $P (A) > P (B)$ .

Ćwiczenie 33

W pewnej grze losowej zakreślamy $6$ liczb wybranych ze zbioru ${1, 2, 3, . . ., 49}$ . Wybrane liczby są następnie porównywane z sześcioma wylosowanymi z tego samego zbioru przez maszynę losującą. Oblicz prawdopodobieństwo $p$ tego, że zakreślając $6$ liczb trafisz główną wygraną, czyli prawidłowo wytypujesz wszystkie $6$ wylosowanych numerów.

$p = \frac{1}{13983816}$

Każde zdarzenie elementarne to wybór sześcioelementowego podzbioru ze zbioru $49$ liczb $\{1, 2, 3, . . ., 49\}$ . Wszystkich zdarzeń elementarnych jest więc $|Ω| = (\begin{array}{l} 49 \\ 6 \end{array}) = \frac{49!}{6! \cdot 43!} = \frac{49 \cdot 48 \cdot 47 \cdot 46 \cdot 45 \cdot 44}{6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1} = 13 983 816$ . Prawidłowo wytypować wygraną można, oczywiście, tylko na $1$ sposób, więc $p = \frac{1}{13983816}$ (szansa $1$ do prawie $14$ milionów).

Zadania

Klasyczna definicja prawdopodobieństwa (treść rozszerzona)

Klasyczna definicja prawdopodobieństwa. Własności prawdopodobieństwa. Obliczanie prawdopodobieństw zdarzeń losowych

Pojęcie prawdopodobieństwa

Własności prawdopodobieństwa

Doświadczenia dwuetapowe - metoda drzewa