Wielokąty, koła i okręgi
9. Koła i okręgi
Wiele osób zapewne zgodzi się ze stwierdzeniem: Pizza jest najbardziej matematycznym jedzeniem na świecie. Jest ku temu kilka powodów. Najważniejszym z nich jest fakt, że sama w sobie stanowi wykres kołowy ilości pizzy, która pozostała do zjedzenia. Nie mniej istotną jest obserwacja, iż w samej nazwie posiada ona przedrostek „pi”, zaś liczba pojawia się we wzorach opisujących zależność obwodu oraz pola pizzy od jej promienia.
Koło jest figurą wyjątkową. Przy ustalonym obwodzie jest figurą posiadającą największe pole. Podobną cechę ma bańka mydlana. Ma ona kształt kuli (a dokładniej sfery). Przy ustalonej powierzchni ma największą objętość.
Materiał zawiera podstawowe pojęcia związane z okręgiem i kołem. Utrwalisz zdobytą wiedzę, wykonując ćwiczenia. Test końcowy, pomoże Ci określić stopień ukształtowanych umiejętności dotyczących własności kół i okręgów oraz wzajemnego położenia dwóch okręgów.
Okrąg
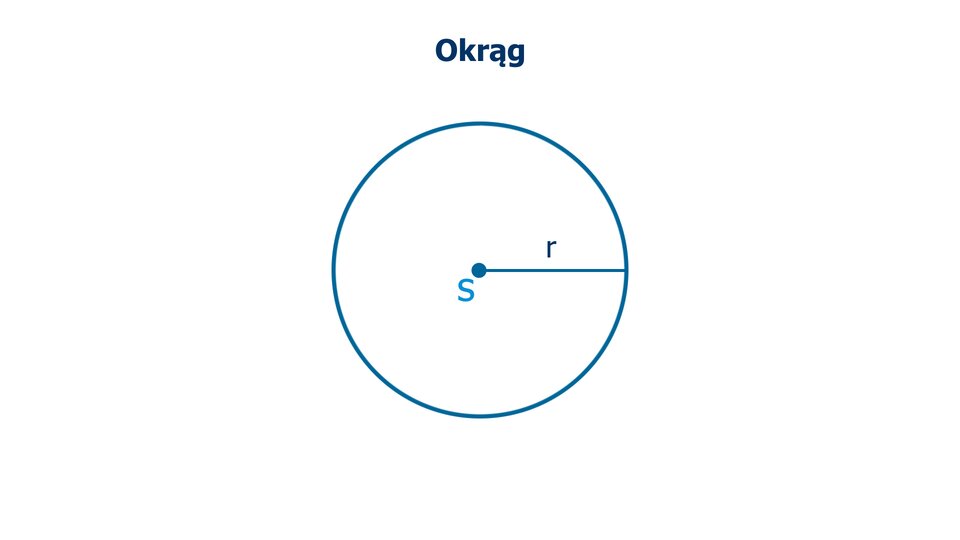
Okręgiem nazywamy figurę złożoną ze wszystkich punktów płaszczyzny równo oddalonych od ustalonego punktu zwanego środkiem okręgu.
Film dostępny pod adresem /preview/resource/R1RmphvuqzJHo
Animacja przedstawia rysowanie okręgu z punktem S w jego środku oraz z odległością r od punktu S do okręgu.

Punkty okręgu są jednakowo oddalone od jego środka. Tę odległość oraz odcinek łączący punkt na okręgu ze środkiem okręgu nazywamy promieniem okręgu.
Narysujemy okrąg za pomocą cyrkla.

Film dostępny pod adresem /preview/resource/RkhUO4KQGf2y5
Animacja przedstawia konstrukcję okręgu za pomocą cyrkla.
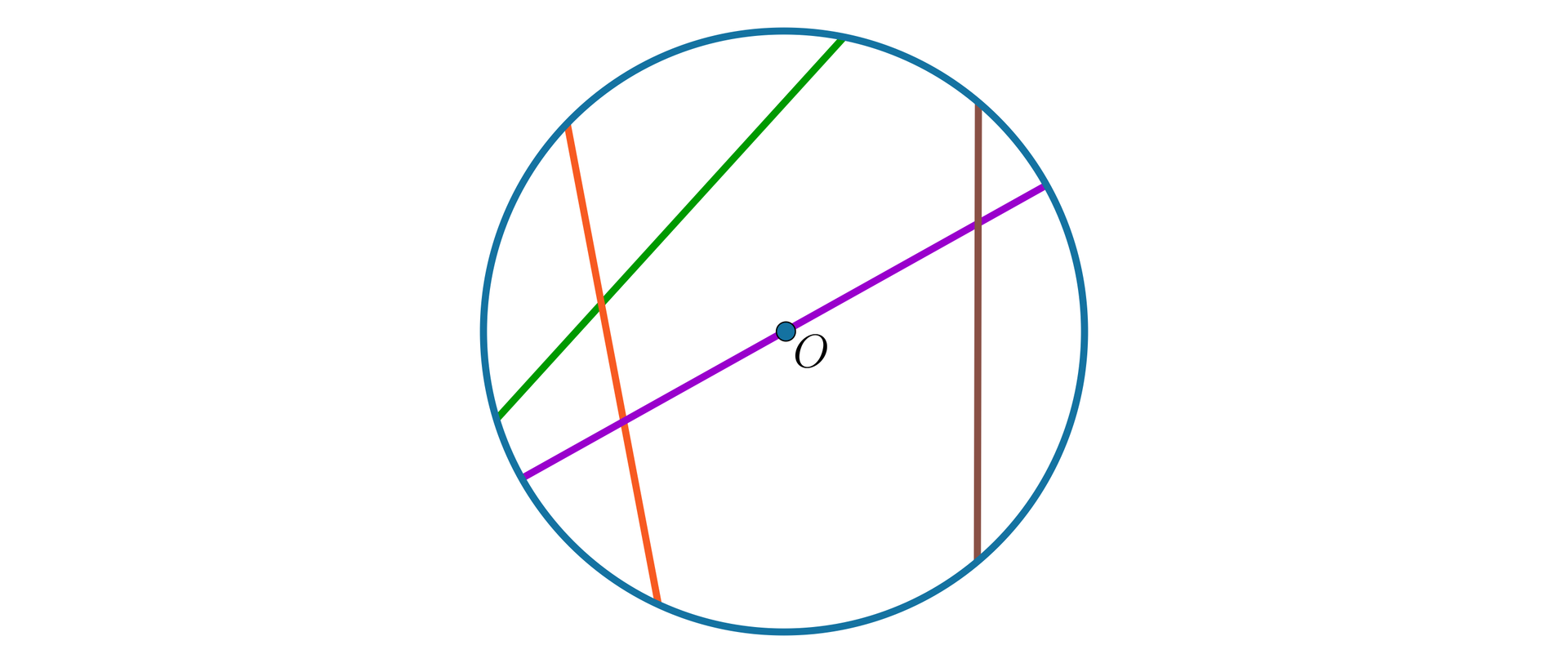
Każdy odcinek, którego końce leżą na okręgu, nazywamy cięciwą okręgu.
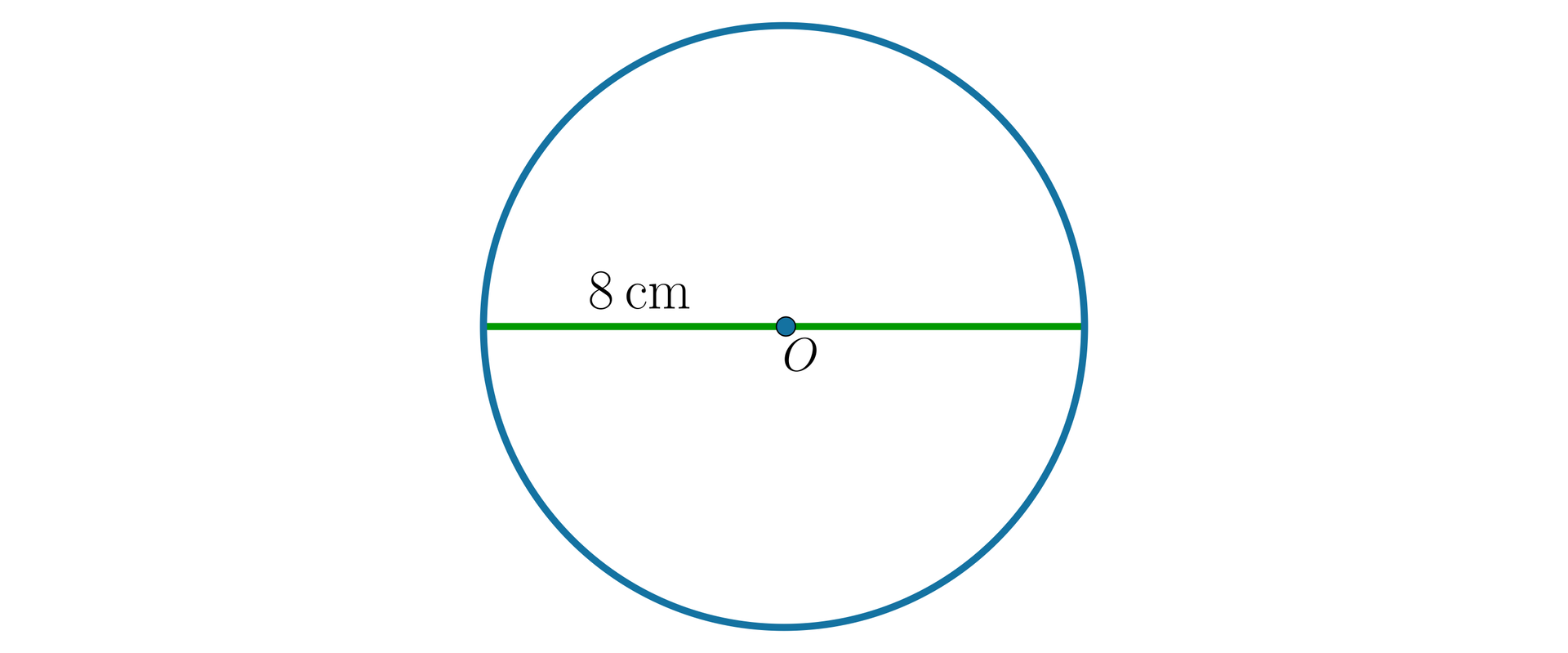
Cięciwę, która przechodzi przez środek okręgu, nazywamy średnicą okręgu.

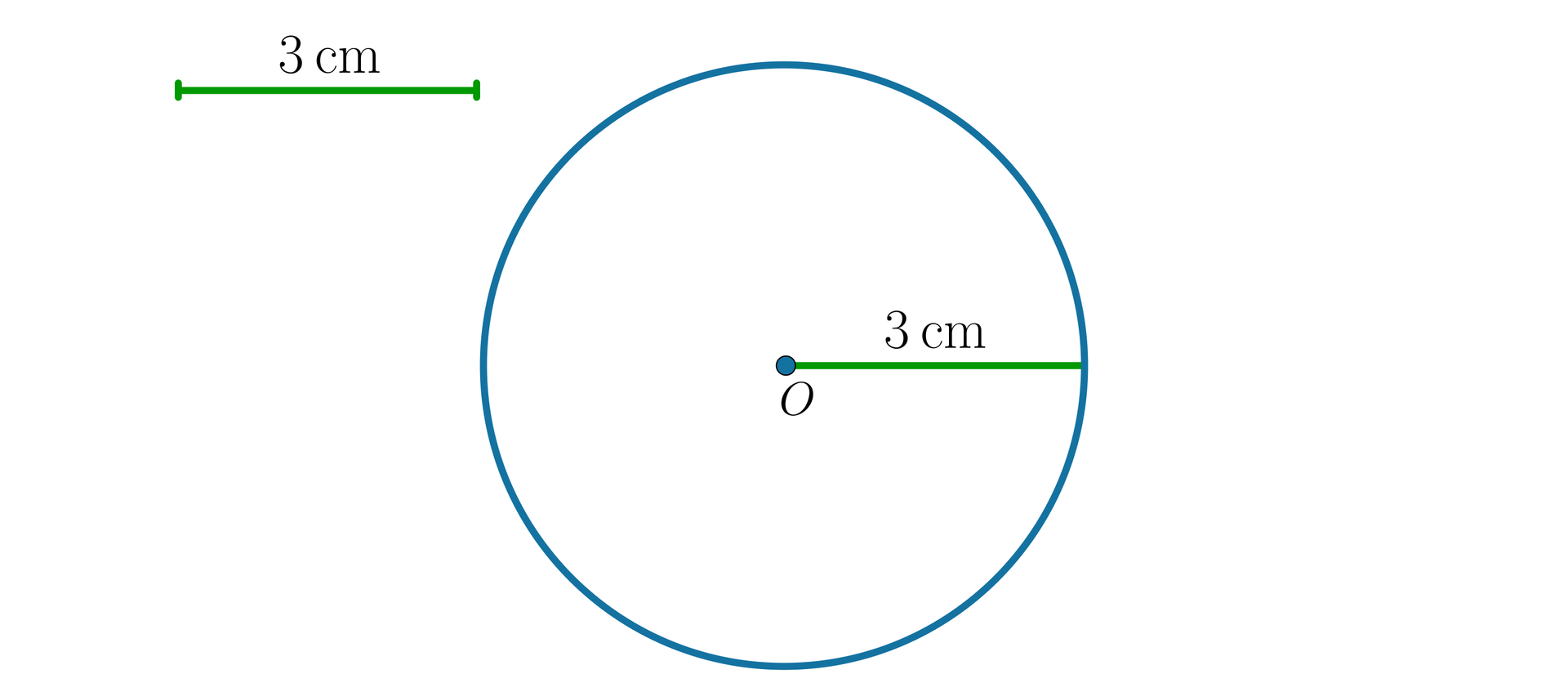
Odcinek łączący środek okręgu z punktem leżącym na okręgu nazywamy promieniem okręgu.
Oznaczamy go najczęściej małą literą .

Koło
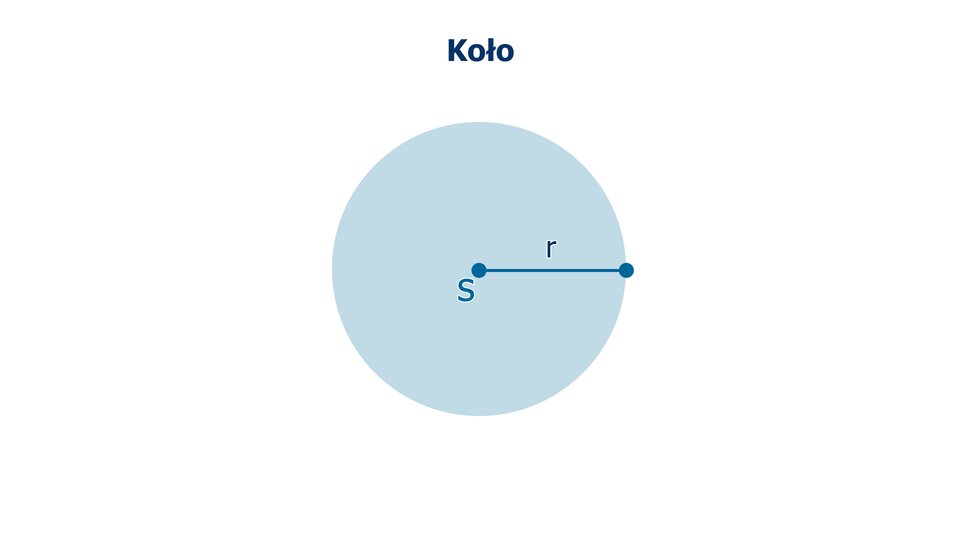
Kołem o środku w punkcie i promieniu nazywamy figurę zbudowaną ze wszystkich punktów płaszczyzny, których odległość od punktu jest mniejsza bądź równa promieniowi.
Film dostępny pod adresem /preview/resource/RubxIVsX9Zz51
Animacja przedstawia rysowanie koła o środku w punkcie S i promieniu r.
Czy wiesz czym różni się koło od okręgu? Co nazywamy promieniem, a co średnicą okręgu? Ile cięciw może mieć koło? A okrąg? Czy środek okręgu należy do okręgu? A środek koła czy należy do koła? Czy okrąg ma „grubość”?
Film dostępny pod adresem /preview/resource/RdSCBwIHgGn5s
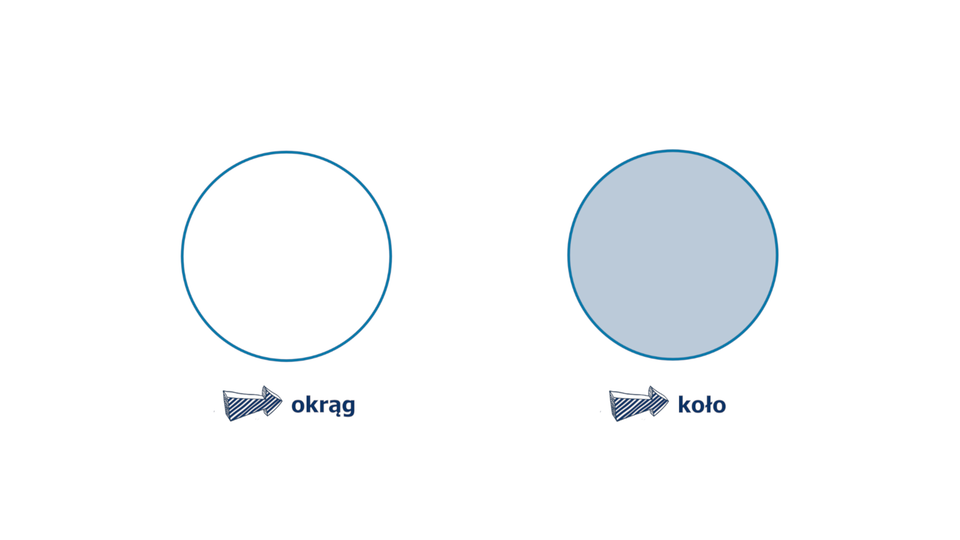
Zestawienie koła i okręgu.
Pamiętaj pomiędzy kołem i okręgiem jest zasadnicza różnica. Okrąg jest brzegiem koła.
Elementy koła
Film dostępny pod adresem /preview/resource/R18Ifh3WKLyYK
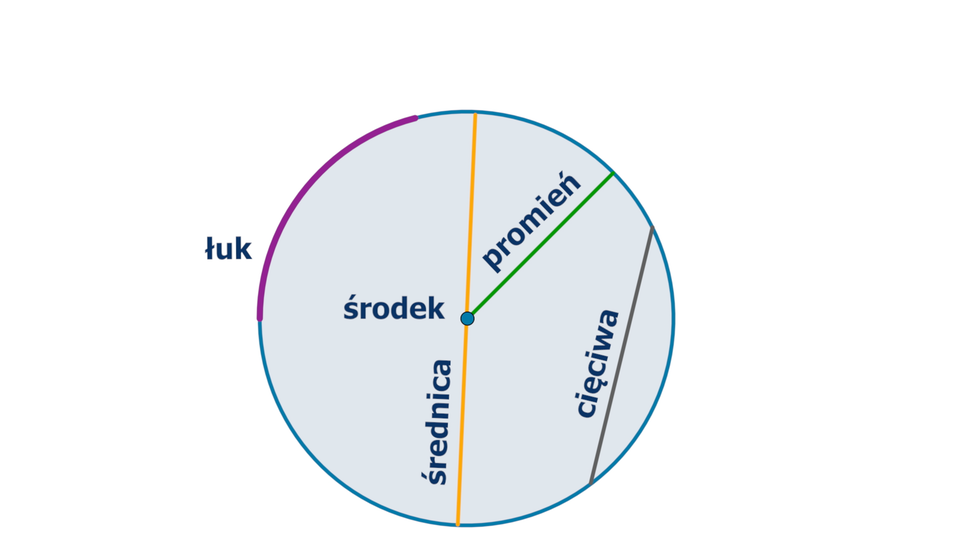
Animacja przedstawia koło oraz wyróżnione w nim szczególne elementy.
Promień koła – odcinek łączący środek koła z punktem leżącym na okręgu, będącym brzegiem tego koła. Promień to również długość tego odcinka.
Cięciwa koła – odcinek łączący dwa punkty leżące na okręgu, będącym brzegiem tego koła.
Średnica koła – odcinek łączący dwa punkty leżące na okręgu, będącym brzegiem tego koła, przechodzący przez środek koła. Średnica to najdłuższa cięciwa. Ma ona długość dwóch promieni.
Łuk – część okręgu wyznaczona przez dwa punkty leżące na tym okręgu.
Zapoznaj się z apletem i wykonaj polecenia.
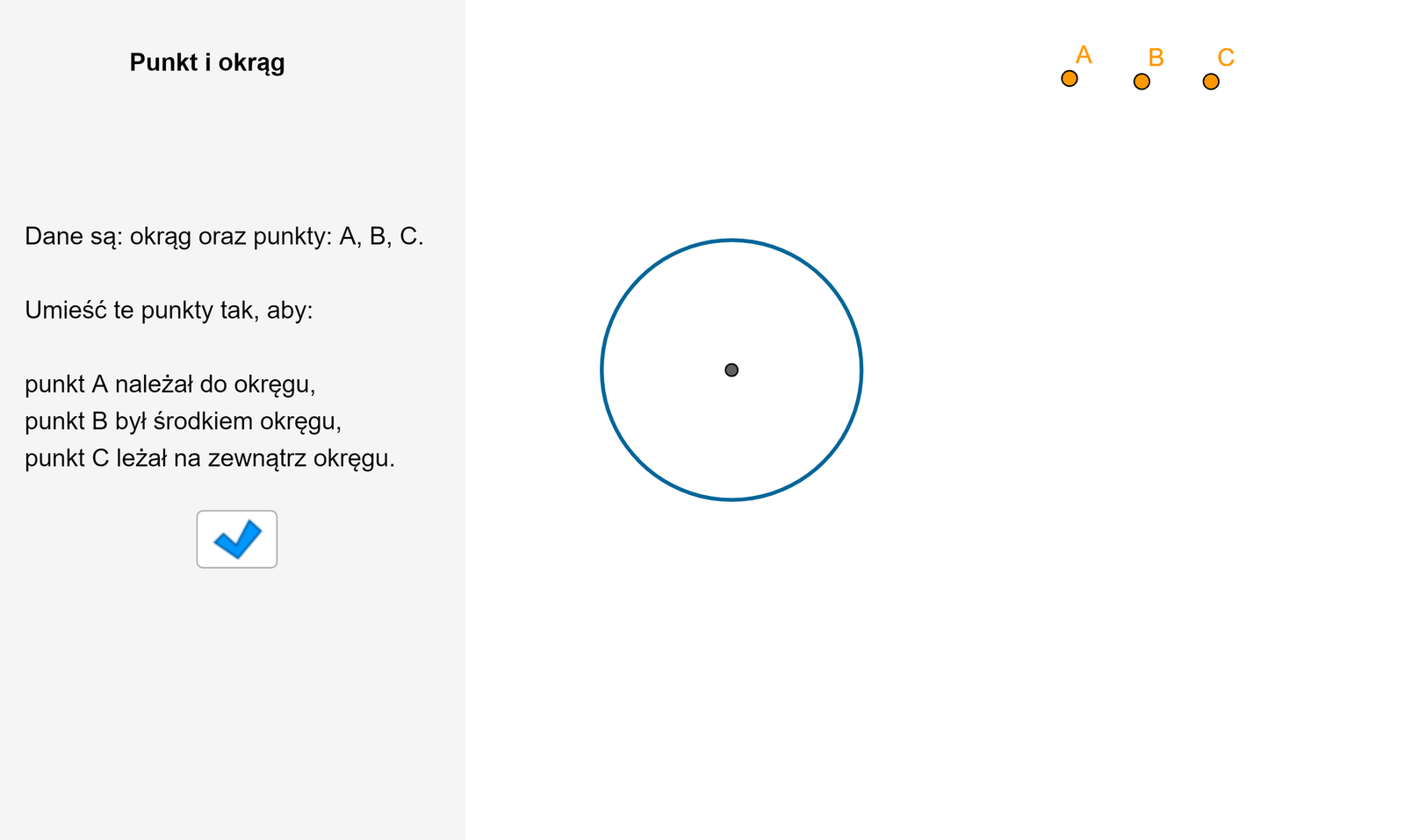
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/D1ATnae4O
Narysuj okrąg oraz trzy cięciwy niebędące średnicami oraz jedną cięciwę będącą średnicą tego okręgu.
Narysuj okrąg i odcinek łączący środek okręgu z dowolnym punktem na okręgu. Ile razy ten odcinek jest krótszy od średnicy okręgu?
dwa razy, trzy razy, cztery razy
Odcinek łączący środek okręgu z punktem leżącym na okręgu jest ...................... krótszy od średnicy tego okręgu.
Do każdego z pytań wybierz prawidłową odpowiedź.
Tak, Nie, Nie, Nie, Tak, Nie, Nie, Tak, Tak, Tak, Tak, Tak, Nie, Tak, Nie, Tak, Nie, Nie
a) Czy promień okręgu jest dwa razy dłuższy od średnicy okręgu? ............
b) Czy promień okręgu jest dwa razy krótszy od średnicy okręgu? ............
c) Czy średnica okręgu jest dwa razy krótsza od promienia okręgu? ............
d) Czy średnica okręgu jest dwa razy dłuższa od promienia okręgu? ............
e) Czy każda cięciwa okręgu jest krótsza od jego średnicy? ............
f) Czy wszystkie promienie okręgu są jednakowej długości? ............
g) Czy cięciwą nazywamy każdy odcinek, którego końce leżą na okręgu? ............
h) Czy średnicą nazywamy każdą cięciwę, która przechodzi przez środek okręgu? ............
i) Czy średnica okręgu jest większa od każdej cięciwy niebędącej średnicą? ............
Narysuj okrąg o średnicy .
Opisz konstrukcję okręgu o średnicy .
Narysuj odcinek długości , a następnie okrąg o promieniu .
Dany jest odcinek o długości . Opisz, jak narysować okrąg o o promieniu .
Narysuj odcinek długości . Następnie narysuj okrąg:
Dany jest odcinek długości . Opisz, jak narysować okrąg:
o środku w punkcie i promieniu ,
o środku w punkcie i promieniu .
Policz, ile kół jest przedstawionych na poniższym rysunku.


Skonstruuj koło o promieniu równym .
Opisz konstrukcję koła o promieniu równym .
Skonstruuj koło i okrąg o promieniu .
Opisz konstrukcję koła i okręgu o promieniu .
Zapoznaj się z apletem i wykonaj polecenia.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/D1ATnae4O
b) Brzeg koła jest 1. dłuższa, 2. promień, 3. środek, 4. promień, 5. krótsza, 6. średnica, 7. cięciwa, 8. środkiem, 9. środek, 10. średnicą, 11. środek, 12. promień, 13. średnica, 14. średnica, 15. okręgiem, 16. promieniem.
c) Odcinek łączący środek koła z punktem leżącym na brzegu koła to 1. dłuższa, 2. promień, 3. środek, 4. promień, 5. krótsza, 6. średnica, 7. cięciwa, 8. środkiem, 9. środek, 10. średnicą, 11. środek, 12. promień, 13. średnica, 14. średnica, 15. okręgiem, 16. promieniem.
d) Średnica koła jest dwa razy 1. dłuższa, 2. promień, 3. środek, 4. promień, 5. krótsza, 6. średnica, 7. cięciwa, 8. środkiem, 9. środek, 10. średnicą, 11. środek, 12. promień, 13. średnica, 14. średnica, 15. okręgiem, 16. promieniem od promienia koła.
e) Dwie cięciwy przecięły się w środku koła. Każda z tych cięciw to 1. dłuższa, 2. promień, 3. środek, 4. promień, 5. krótsza, 6. średnica, 7. cięciwa, 8. środkiem, 9. środek, 10. średnicą, 11. środek, 12. promień, 13. średnica, 14. średnica, 15. okręgiem, 16. promieniem koła.
Wybierz.
okręgiem, cięciwa, środek, średnica, środkiem, promieniem, krótsza, środek, średnica, środek, dłuższa, średnicą, średnica, promień, promień, promień
a) Najdłuższą cięciwą koła jest .....................
b) Brzeg koła jest .....................
c) Odcinek łączący środek koła z punktem leżącym na brzegu koła to .....................
d) Średnica koła jest dwa razy .................... od promienia koła.
e) Dwie cięciwy przecięły się w środku koła. Każda z tych cięciw to .................... koła.
Uzupełnij zdanie. Koza wygryzła trawę w kole o średnicy Tu uzupełnij i o promieniu Tu uzupełnij .
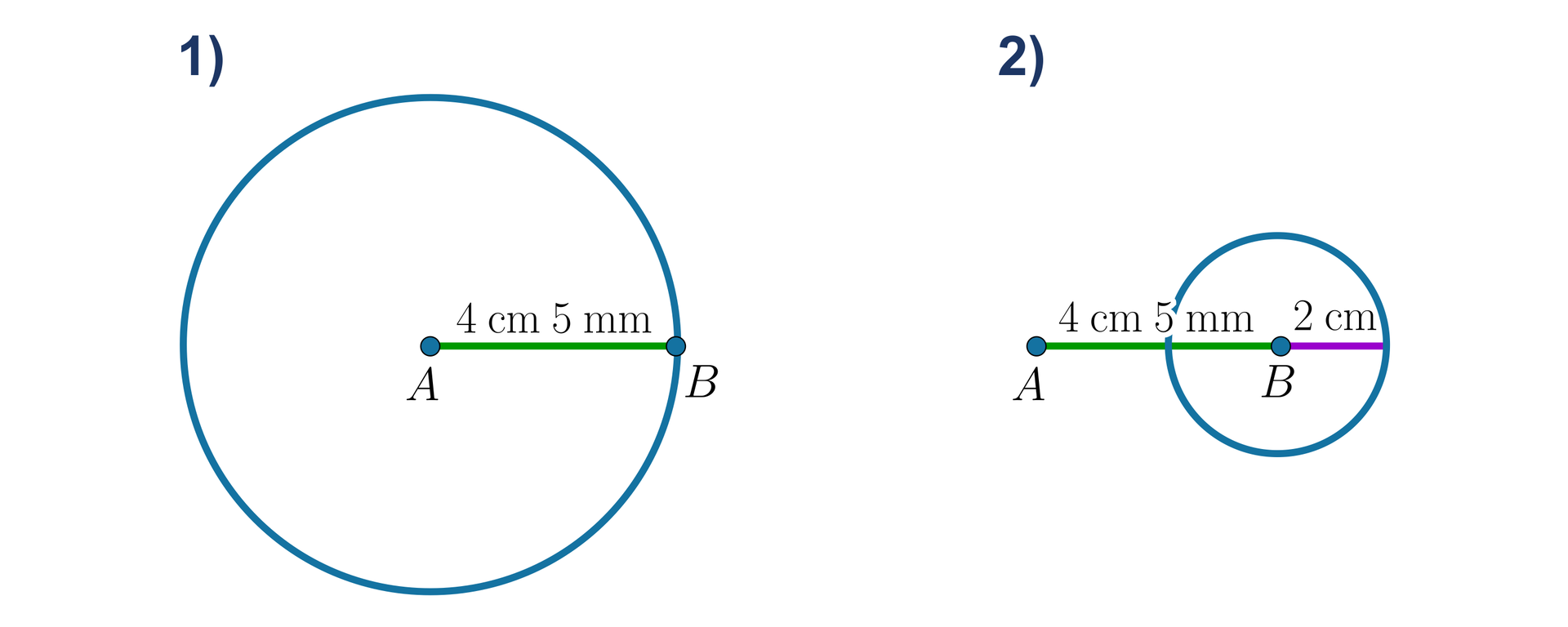
Promień jednego z okręgów ma długość , drugiego zaś . Jaka jest odległość między środkami tych okręgów? Zaznacz poprawną odpowiedź.

Promień jednego z okręgów ma długość , drugiego zaś . Jaka jest odległość między środkami tych okręgów, jeżeli okręgi się przecinają, a szerokość tego przecięcia wynosi ? Zaznacz poprawną odpowiedź.
Poniżej narysowano siedem okręgów.

Który element na rysunku uznasz za koło, a który za okrąg?
Który element monety uznasz za koło, a który za okrąg?

Za pomocą cyrkla narysuj poniższe kwiatki.
R9G7q8VuND5qX1  Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.Zaprojektuj wzorek zbudowany z okręgów.
Opisz, jak za pomocą okręgów można skonstruować rysunek kwiatka.
Narysuj okrąg o środku w punkcie i promieniu . Zaznacz na okręgu dwa różne punkty i .
Jaką długość ma średnica tego okręgu?
Jaką długość ma odcinek ?
Jaką największą długość może mieć odcinek ?
Okrąg o środku w punkcie i promieniu to zbiór wszystkich punktów płaszczyzny, których odległość od punktu Możliwe odpowiedzi: 1. jest równa ., 2. jest mniejsza lub równa ., 3. jest większa lub równa ., 4. jest równa .
- jest równa
- jest mniejsza lub równa
- jest większa lub równa
- jest równa
Koło o środku w punkcie i promieniu to zbiór wszystkich punktów płaszczyzny, których odległość od punktu Możliwe odpowiedzi: 1. jest równa ., 2. jest mniejsza lub równa ., 3. jest większa lub równa ., 4. jest równa .
- jest równa
- jest mniejsza lub równa
- jest większa lub równa
- jest równa
Promieniem okręgu nazywamy Możliwe odpowiedzi: 1. każdą z cięciw., 2. każdy odcinek, którego jednym końcem jest środek okręgu, a drugi leży na okręgu., 3. każdy odcinek, którego końce leżą na okręgu., 4. każdą z cięciw, która przechodzi przez środek okręgu.
- każdą z cięciw
- każdy odcinek, którego jednym końcem jest środek okręgu, a drugi leży na okręgu
- każdy odcinek, którego końce leżą na okręgu
- każdą z cięciw, która przechodzi przez środek okręgu
Średnicą okręgu nazywamy Możliwe odpowiedzi: 1. każdą z cięciw., 2. odcinek, którego jednym końcem jest środek okręgu, a drugi leży na okręgu., 3. cięciwę, do której należy środek okręgu., 4. każdy odcinek, którego końce leżą na okręgu.
- każdą z cięciw
- odcinek, którego jednym końcem jest środek okręgu, a drugi leży na okręgu
- cięciwę, do której należy środek okręgu
- każdy odcinek, którego końce leżą na okręgu
Cięciwą okręgu nazywamy Możliwe odpowiedzi: 1. odcinek równy długości połowy średnicy., 2. każdy odcinek, którego jednym końcem jest środek okręgu, a drugi leży na okręgu., 3. połowę średnicy., 4. każdy odcinek, którego końce leżą na okręgu.
- odcinek równy długości połowy średnicy
- każdy odcinek, którego jednym końcem jest środek okręgu, a drugi leży na okręgu
- połowę średnicy
- każdy odcinek, którego końce leżą na okręgu
- Tak, ponieważ dwa boki trójkąta są równe promieniowi okręgu.
- Nie, ponieważ trójkąt jest prostokątny.
- Tak, ponieważ trójkąt jest prostokątny.
- Nie, ponieważ dwa boki trójkąta są równe promieniowi okręgu.
Ile różnych okręgów może przechodzić przez dwa różne punkty?
A przez trzy? A przez cztery? Uzasadnij odpowiedź.
Koła i okręgi
Test wiadomości z materiału „Koła i okręgi”.
Notatnik
Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.