Słowniczek
Jeżeli dwa trójkąty mają odpowiadające sobie boki równe, to te trójkąty są przystające.

Jeżeli to trójkąt jest przystający do trójkąta .
Zapisujemy symbolicznie
Jeżeli dwa boki i kąt zawarty pomiędzy nimi w jednym trójkącie, są równe dwóm bokom i kątowi zawartemu między nimi w drugim trójkącie, to te trójkąty są przystające.

Jeżeli to trójkąt jest przystający do trójkąta
Jeżeli bok i dwa przyległe do niego kąty w jednym trójkącie są odpowiednio równe bokowi i dwóm przyległym do niego kątom drugiego trójkąta, to trójkąty te są przystające.

Jeżeli i , to trójkąt jest przystający do trójkąta .
Deltoidem nazywamy czworokąt, którego jedna z przekątnych leży na jego osi symetrii.

Jeżeli dwie proste przecięte są trzecią prostą i utworzone w ten sposób kąty odpowiadające są równe, to proste te są równoległe.
Jeżeli dwie proste przecięte są trzecią prostą i utworzone w ten sposób kąty naprzemianległe są równe, to proste te są równoległe.
Dwusieczną kąta trójkąta nazywamy półprostą o początku w wierzchołku tego kąta, która dzieli ten kąt na dwa kąty o jednakowych miarach.

Dwusieczną kąta nazywamy półprostą o początku w wierzchołku tego kąta, która dzieli ten kąt na dwa kąty o jednakowych miarach.

Figurę nazywamy osiowosymetryczną, jeżeli istnieje taka prosta , iż każdy punkt figury po przekształceniu w symetrii względem prostej należy do figury . Weźmy trzy przykładowe punkty i znajdźmy obrazy , , tych punktów w symetrii względem prostej .
Prostą nazywamy osią symetrii figury .

Film dostępny na portalu epodreczniki.pl
Animacja
Figurę nazywamy środkowosymetryczną, jeżeli istnieje taki punkt , że obraz każdego punktu figury w symetrii względem punktu też należy do tej figury. Punkt nazywamy wtedy środkiem symetrii figury .

Figury, które mają ten sam kształt i tę samą wielkość nazywamy przystającymi.
Jednomianem nazywamy wyrażenie algebraiczne, które jest liczbą, literą lub iloczynem liczb i liter.
Jednomianami podobnymi nazywamy jednomiany, w których występują takie same czynniki literowe w tej samej potędze.
Jednomiany podobne różnią się współczynnikiem liczbowym lub kolejnością czynników. Jednomiany podobne występujące w sumie algebraicznej nazywamy wyrazami podobnymi sumy algebraicznej.
Dwie półproste o wspólnym początku rozcinają płaszczyznę na dwie części. Każdą z tych części, wraz z tymi półprostymi nazywamy kątem.
Wierzchołkiem kąta nazywamy wspólny początek obu półprostych, a każdą z półprostych nazywamy ramieniem kąta.
Proste i są przecięte prostą
Kąty: i , i i oraz i to pary kątów odpowiadających.
Kąty i oraz i to pary kątów naprzemianległych wewnętrznych.
Kąty i oraz i to pary kątów naprzemianległych zewnętrznych.
Rgeu2bwtCJ8GF1
Kąty przyległe to dwa kąty wypukłe, które mają jedno ramię wspólne, a pozostałe ramiona dopełniają się do prostej.
Kąty wierzchołkowe to dwa kąty wypukłe, które mają wspólny wierzchołek i przedłużeniem ramion jednego kąta są odpowiednie ramiona drugiego kąta.
R17EFmv3QSulO1 Na przykład i na rysunku są kątami przyległymi. Pary kątów wierzchołkowych to i oraz i
Jeżeli dwie proste równoległe przetniemy trzecią prostą, to tak utworzone kąty odpowiadające są równe.
R1I2tUoI64raX1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.Jeżeli dwie proste równoległe przetniemy trzecią prostą, to tak utworzone kąty naprzemianległe wewnętrzne są równe oraz kąty naprzemianległe zewnętrzne są równe.
R18ZZPCMdXMZf1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Dwa kąty o równych miarach są przystające.
Kąty wierzchołkowe mają równe miary.
Kąty, których miara jest mniejsza od lub równa nazywamy kątami wypukłymi.
Kąty, których miara jest większa od , ale mniejsza od , to kąty wklęsłe.
RHzS3D7shCIkp1  Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Kątem zewnętrznym trójkąta nazywamy każdy kąt przyległy do kąta wewnętrznego tego trójkąta.

– kąty zewnętrzne, przyległe do kąta
Kołem o środku w punkcie i promieniu nazywamy zbiór tych punktów płaszczyzny, których odległość od punktu jest mniejsza bądź równa .

– koło o środku w punkcie i promieniu
Liczba przeciwna do danej liczby to taka liczba , że zachodzi równość
Liczba spełnia dane równanie, jeżeli po podstawieniu jej w miejsce niewiadomej i wykonaniu działań po obu stronach równania, otrzymamy prawdziwą równość liczbową.
Mówimy, że liczba spełnia daną nierówność, jeżeli po wstawieniu jej w miejsce niewiadomej i wykonaniu wskazanych działań otrzymamy nierówność liczbową prawdziwą.
Na przykład:
Sprawdzimy, czy liczba spełnia nierówność
Podstawmy w miejsce
Nierówność jest prawdziwa.
Liczba spełnia daną nierówność. Liczba jest jednym z rozwiązań nierówności.
Liczba wymierna to liczba, którą można przedstawić w postaci ułamka gdzie i są liczbami całkowitymi i .
Liczbę naturalną większą od nazywamy liczbą pierwszą, jeżeli jej jedynymi dzielnikami są liczby i . Liczby naturalne większe od , które nie są liczbami pierwszymi nazywamy liczbami złożonymi. Liczby i nie są ani liczbami pierwszymi, ani złożonymi.
Liczbami wymiernymi są liczby naturalne, całkowite i ułamki.

Najmniejszą wspólną wielokrotnością liczb naturalnych dodatnich i (oznaczamy nazywamy najmniejszą liczbę naturalną dodatnią, która jest podzielna przez liczbę i liczbę .
Największym wspólnym dzielnikiem dodatnich liczb naturalnych i (oznaczamy nazywamy największą liczbę naturalną, która jest jednocześnie dzielnikiem liczby i liczby .
Nierówności nazywamy równoważnymi, jeżeli posiadają ten sam zbiór rozwiązań.
Nierównością pierwszego stopnia z jedną niewiadomą nazywamy nierówność, w której występuje dokładnie jedna niewiadoma w pierwszej potędze.
Na przykład
W dowolnym trójkącie długość każdego boku jest mniejsza od sumy długości pozostałych boków.
Z odcinków o długościach można zbudować trójkąt wtedy i tylko wtedy, gdy
Obrazem figury w symetrii środkowej jest figura do niej przystająca.
Obrazem figury w symetrii osiowej jest figura do niej przystająca.
Obwód wielokąta to suma długości wszystkich jego boków.
Część prostej zawartej między dwoma punktami, wraz z tymi punktami, to odcinek.
Odległość między dwiema dowolnymi liczbami na osi liczbowej jest równa długości odcinka łączącego punkty odpowiadające tym liczbom.
Odległość środka okręgu wpisanego w wielokąt od każdego z boków tego wielokąta jest równa promieniowi tego okręgu.
Liczba odwrotna do danej liczby , to taka liczba , że
Odwrotnością liczby , gdzie jest liczba .
Okręgiem o środku w punkcie i promieniu nazywamy zbiór tych wszystkich punktów płaszczyzny, których odległość od punktu jest równa .

– okrąg ośrodku w punkcie i promieniu
Jeżeli na okręgu leżą wszystkie wierzchołki trójkąta, to taki okrąg nazywamy okręgiem opisanym na trójkącie. O trójkącie mówimy, że jest wpisany w okrąg.

Na każdym trójkącie można opisać okrąg. Środek tego okręgu leży na przecięciu symetralnych boków tego trójkąta.
Jeśli każdy z boków wielokąta jest styczny do okręgu, to ten wielokąt nazywamy opisanym na okręgu. Okrąg nazywamy wtedy wpisanym w wielokąt.
Punkt, w którym przecinają się proste zawierające wysokości trójkąta nazywamy ortocentrum trójkąta i oznaczamy go najczęściej dużą literą .
Pole równoległoboku jest równe iloczynowi wysokości równoległoboku i długości podstawy, do której ta wysokość została poprowadzona.

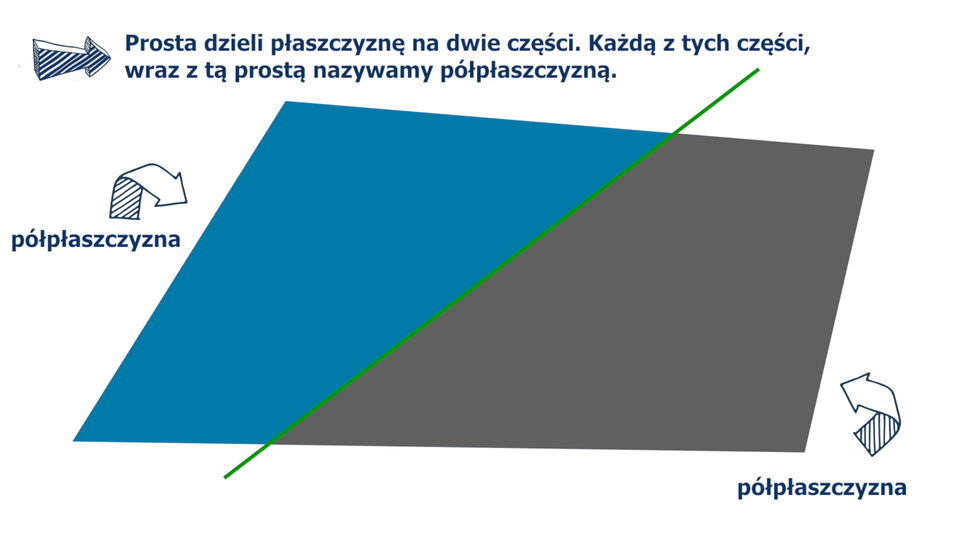
Prosta dzieli płaszczyznę na dwie części. Każdą z nich wraz z tą prostą nazywamy półpłaszczyzną. Prosta ta jest brzegiem każdej z tych półpłaszczyzn.
Film dostępny na portalu epodreczniki.pl
Animacja
Jeden procent to jedna setna.
Jeden promil to jedna tysięczna.
Równość postaci dla nazywamy proporcją.
Wyrazy i nazywają się skrajnymi, a wyrazy i środkowymi.
Przez jeden punkt przechodzi nieskończenie wiele prostych.
Przez dwa różne punkty przechodzi dokładnie jedna prosta.
Przekątna wielokąta to odcinek łączący dwa wierzchołki tego wielokąta, nieleżące przy tym samym boku.
Niech będzie liczbą naturalną większą od .
Wielokąt o – bokach ma przekątnych.
Dwa kwadraty są przystające, jeżeli ich boki są równe lub równe są ich przekątne.

Dwusieczne kątów trójkąta przecinają się w jednym punkcie.

Redukcją wyrazów podobnych nazywamy przekształcenie sumy algebraicznej polegające na wykonaniu dodawania lub odejmowania wyrazów podobnych. W wyniku redukcji wyrazów podobnych, otrzymujemy prostszą postać sumy algebraicznej.
Kąt, którego miara jest mniejsza od , ale większa od , nazywamy kątem ostrym.
Kąt, którego miara jest równa , nazywamy kątem prostym.
Kąt, którego miara jest większa od , ale mniejsza od , nazywamy kątem rozwartym.
RMy9sLyDS4AHh1 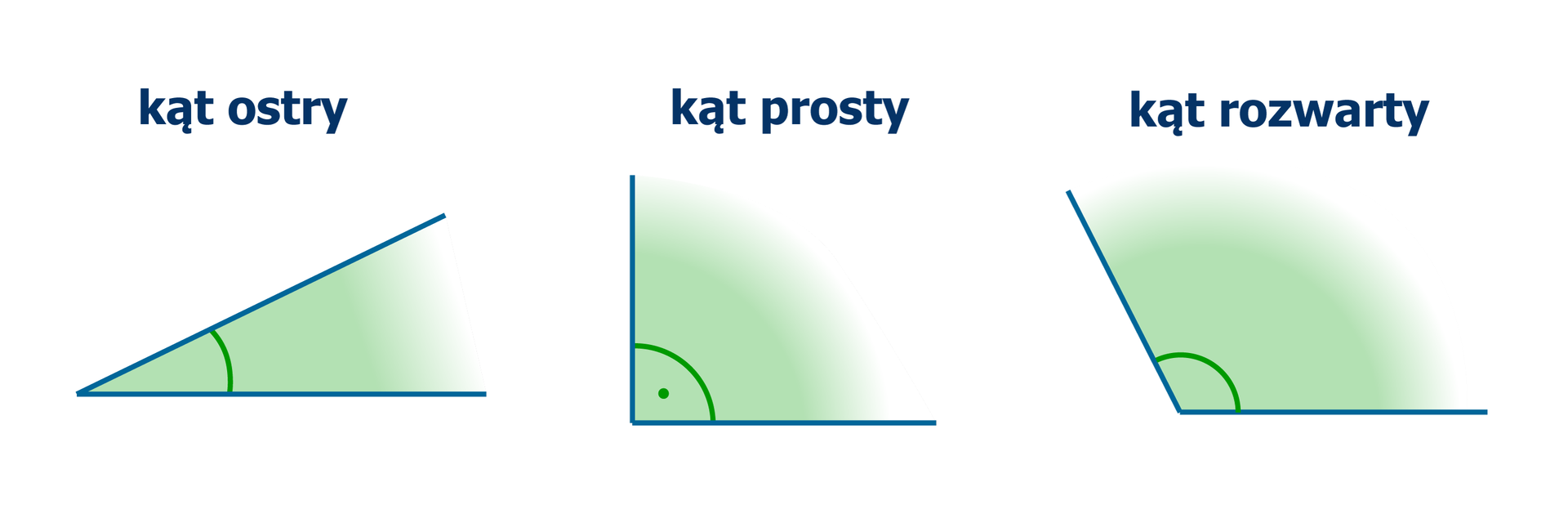 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Jeśli w równoległoboku wszystkie boki są równe, to równoległobok nazywamy rombem.
Liczbę, która spełnia dane równanie nazywamy rozwiązaniem lub pierwiastkiem równania.
Każdy ułamek zwykły ma rozwinięcie dziesiętne skończone lub nieskończone okresowe.
Mówimy, że równania z tymi samymi niewiadomymi są równoważne wtedy i tylko wtedy, gdy posiadają taki sam zbiór rozwiązań.
Równaniem nazywamy równość dwóch wyrażeń algebraicznych, z których w przynajmniej jednym występuje co najmniej jedna zmienna, zwana niewiadomą.
Na przykład:
Równaniem pierwszego stopnia z jedną niewiadomą (liniowym) nazywamy równanie, w którym niewiadoma występuje w pierwszej potędze.
Na przykład
Równanie, które nie ma rozwiązania nazywamy równaniem sprzecznym.
Równanie, które jest spełnione przez każdą liczbę rzeczywistą nazywamy równaniem tożsamościowym.
Równaniem z jedną niewiadomą nazywamy równość dwóch wyrażeń algebraicznych, w których występuje dokładnie jedna niewiadoma.
Na przykład
Czworokąt, który ma dwie pary boków równoległych, nazywamy równoległobokiem.

Prostą mającą dwa punkty wspólne z okręgiem nazywamy sieczną okręgu.
Stosunkiem dwóch wielkości nazywamy iloraz odpowiadających sobie wartości tych wielkości. Zapisuje się go zwykle w postaci ilorazu liczb naturalnych.
Prostą mającą dokładnie jeden punkt wspólny z okręgiem nazywamy styczną do okręgu.
Sumą algebraiczną nazywamy wyrażenie, które jest sumą jednomianów. Jednomiany te nazywamy wyrazami sumy.
Wyrażenie algebraiczne, w którym występuje odejmowanie jednomianów, jest także sumą algebraiczną, ponieważ odejmowanie możemy zastąpić dodawaniem jednomianów przeciwnych.
Suma miar kątów leżących przy jednym z ramion trapezu jest równa .
Niech będzie liczbą naturalną większą od .
Suma miar kątów – kąta jest równa .
Suma miar kątów trójkąta jest równa

Symetralna odcinka to prosta prostopadła do tego odcinka, przechodząca przez jego środek.

.
Punkt jest symetryczny do punktu względem prostej jest obrazem punktu w symetrii względem prostej jeżeli
punkty i leżą na prostej prostopadłej do prostej
punkty i leżą po przeciwnych stronach prostej
odległość punktu od prostej jest taka sama jak odległość punktu od prostej
R12dDiQfZbTbG1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.Jeżeli punkt leży na prostej to .
Rp0GSY70nQzAN1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.Symetrię względem prostej nazywamy symetrią osiową.
Punkt jest symetryczny do punktu względem punktu jest obrazem punktu w symetrii względem punktu jeżeli
leży na prostej po przeciwnej stronie punktu niż punkt
jego odległość od punktu jest równa odległości punktu od punktu .
Symetrię względem punktu nazywamy symetrią środkową.
Środek ciężkości trójkąta dzieli każdą z środkowych tego trójkąta w stosunku , licząc od wierzchołka.

Środkową boku trójkąta nazywamy odcinek łączący wierzchołek trójkąta ze środkiem przeciwległego boku. Trójkąt ma trzy środkowe.
Jeśli czworokąt ma co najmniej jedną parę boków równoległych, to nazywamy go trapezem.

Boki równoległe trapezu nazywamy jego podstawami, zaś dwa pozostałe boki to ramiona trapezu.
Trapez, w którym przynajmniej jeden kąt ma miarę nazywamy trapezem prostokątnym.

W trapezie prostokątnym ramię prostopadłe do podstawy jest zarazem wysokością.
Trapez, którego ramiona są równe i niebędący równoległobokiem nazywamy trapezem równoramiennym.

Wartość bezwzględna liczby jest to odległość liczby od zera na osi liczbowej.

Film dostępny na portalu epodreczniki.pl
Animacja przedstawia dwie osie liczbowe z zaznaczonymi punktami od -6 do 6. Na pierwszej osi zaznaczona odległość liczby 5 od liczby 0, równa 5. Zapis: wartość bezwzględna z liczby 5 =5. Na drugiej osi zaznaczona odległość liczby -4 od liczby 0, równa 4. Zapis: wartość bezwzględna z liczby -4 =4.
Dwie wielkości są odwrotnie proporcjonalne, jeżeli wraz ze wzrostem jednej z nich pewną ilość razy, druga maleje tyle samo razy.
Dwie zmienne wielkości dodatnie nazywamy wprost proporcjonalnymi, jeżeli iloraz odpowiadających sobie wartości tych wielkości jest stały.
Wielokątem foremnym nazywamy wielokąt, który ma wszystkie boki równe i wszystkie kąty równe.

Wielokąty przystające mają odpowiadające sobie boki równej długości oraz równe miary odpowiadających sobie kątów.

Liczbę, która występuje na początku uporządkowanego jednomianu nazywamy współczynnikiem liczbowym tego jednomianu.
Wysokością trójkąta nazywamy odcinek łączący wierzchołek trójkąta z prostą, zawierającą przeciwległy bok i prostopadły do tej prostej. Trójkąt ma trzy wysokości.

Zbiór rozwiązań nierówności jest to zbiór wszystkich liczb, które spełniają daną nierówność.
Zbiór wszystkich liczb spełniających dane równanie nazywamy zbiorem rozwiązań równania.







