Wiesz już, że radioaktywne jądra pierwiastków wysyłają promieniowanie $α$ , $β$ i $γ$ . Co się dzieje z jądrami atomów promieniotwórczych? Jakie zmiany w nich zachodzą? Co powstaje w wyniku tych przemian? Jak szybko odbywają się te zmiany? Oprócz pierwiastków radioaktywnych występujących w przyrodzie pojawiają się nowe – są nimi np. odpady promieniotwórcze powstające w elektrowniach jądrowych. Jak długo te odpady pozostaną radioaktywne i będą stanowić zagrożenie? Czytajcie dalej, a znajdziecie odpowiedzi na te pytania.

RebVQP6wVYkpU1

Zdjęcie przedstawia kamienny krąg Stonehenge widziany z odległości kilkudziesięciu metrów. Krąg zajmuje całą szerokość kadru, otaczają go tylko trawa i niebo. Na skraju kadru widoczna jest pomiędzy głazami niewielka grupa ludzi zapewniająca skalę porównawczą dla skał liczących do dziewięciu metrów wysokości. — Na początku XX wieku fizyków fascynowała stała obecność helu w związkach pierwiastków promieniotwórczych. Badania tego fenomenu doprowadziły do odkrycia przewidzianego wcześniej teoretycznie zjawiska przemiany promieniotwórczej pierwiastków. Obecnie wykorzystuje się je m.in. do datowania, czyli określania wieku próbek, znalezisk i monumentów takich jak Stonehenge, który – jak się okazało po badaniach metodą radiowęglową przeprowadzonych w 2008 roku – budowany był stopniowo od około 3100 do 1600 roku p.n.e.

Już potrafisz

stwierdzić, co to jest promieniowanie jądrowe, i wymienić jego najważniejsze rodzaje;
podać definicję promieniowania jonizującego;
wymienić właściwości fizyczne promieniowania alfa, beta i gamma.

Nauczysz się

podawać definicję aktywności pierwiastka;
prawa rozpadu promieniotwórczego;
obliczać liczbę jąder, które jeszcze nie uległy rozpadowi promieniotwórczemu;
podawać definicję czasu połowicznego rozpadu promieniotwórczego;
zapisywać równania przemian jądrowych i przewidywać, jakie nowe jądra powstają w procesie rozpadu promieniotwórczego.

i7e8cV1qjf_d5e164

1. Prawo rozpadu promieniotwórczego

Rozpad promieniotwórczy zachodzi zgodnie z prawem, które nosi nazwę prawa rozpadu promieniotwórczego. Warto podkreślić, że termin ten odnosi się do samorzutnych przemian jąder macierzystych w jądra pochodne. Proces ten jest naturalny i ma charakter statystyczny. Nie możemy przewidzieć, kiedy konkretne jądro ulegnie rozpadowi. Liczba rozpadów będzie tym większa, im większa będzie ilość substancji radioaktywnej i im dłuższy czas będziemy rozpatrywać. Prawo rozpadu dotyczy także izotopów promieniotwórczych uzyskiwanych sztucznie w wyniku reakcji jądrowych.

Można zapisać stosunkowo prostą zależność:

$∆ N = - λ \cdot N (t) \cdot ∆ t$ ,

Oznacza ona, że liczba jąder rozpadających się w czasie $∆ t$ jest proporcjonalna ( $λ$ – współczynnik proporcjonalności zwany stałą rozpadu) do liczby atomów w próbce i do czasu trwania rozpadu. Próbka zawierająca dwa razy więcej jąder danego pierwiastka będzie wysyłać dwa razy więcej cząstek $α$ lub $β$ w tym samym czasie. Oznacza to, że dwa razy więcej jąder będzie ulegać rozpadowi. Znak „ $-$ ” oznacza, że liczba jąder się zmniejsza.

Zapamiętaj!

Wyrażenie:

A (t) = \frac{∆N}{∆t}

nazywamy aktywnością promieniotwórczą. Aktywność oznacza liczbę przemian jądrowych w danej ilości substancji, które zachodzą w określonej jednostce czasu.

Jednostką aktywności promieniotwórczej jest jeden bekerel (Bq):

1 Bq = \frac{1 rozpad}{1 s}

Zapamiętaj!

Aktywność promieniotwórcza jest równa jednemu bekerelowi, jeśli w czasie jednej sekundy następuje jeden rozpad promieniotwórczy.

Polecenie 1

Oblicz aktywność bryłki nieznanej substancji, w której dochodzi do 139 rozpadów promieniotwórczych w ciągu godziny.

My sami i nasze otoczenie stanowimy źródło promieniowania korpuskularnego (wysyłanie cząstek). Poniższa tabela podaje aktywność naturalnych pierwiastków i źródeł (w bekerelach).

Aktywność promieniotwórcza wybranych źródeł naturalnych w odniesieniu do jednostki masy lub objętości
Źródło	Aktywność promieniotwórcza
banan	$125 \frac{Bq}{kg}$
mleko	$50 \frac{Bq}{l}$
woda morska	$12 \frac{Bq}{l}$
granit	$7000 \frac{Bq}{kg}$
5‑letnie dziecko (20 kg)	$600 Bq$
dorosła osoba (70 kg)	$10 000 Bq$

Na podstawie zależności:

$∆ N = - λ \cdot N_{} \cdot ∆ t$

i definicji aktywności, możemy zapisać, że:

$A = λ \cdot N (t)$

Jeżeli liczba jąder radioaktywnych maleje (a tak jest zawsze), to maleje również aktywność promieniotwórcza danej substancji.

R1WhWzxkgsMvR1

Aktywność pierwiastka promieniotwórczego

Aby opisać, jak zmienia się liczba jąder danego pierwiastka z upływem czasu, wygodnie jest wprowadzić pewne pojęcie.

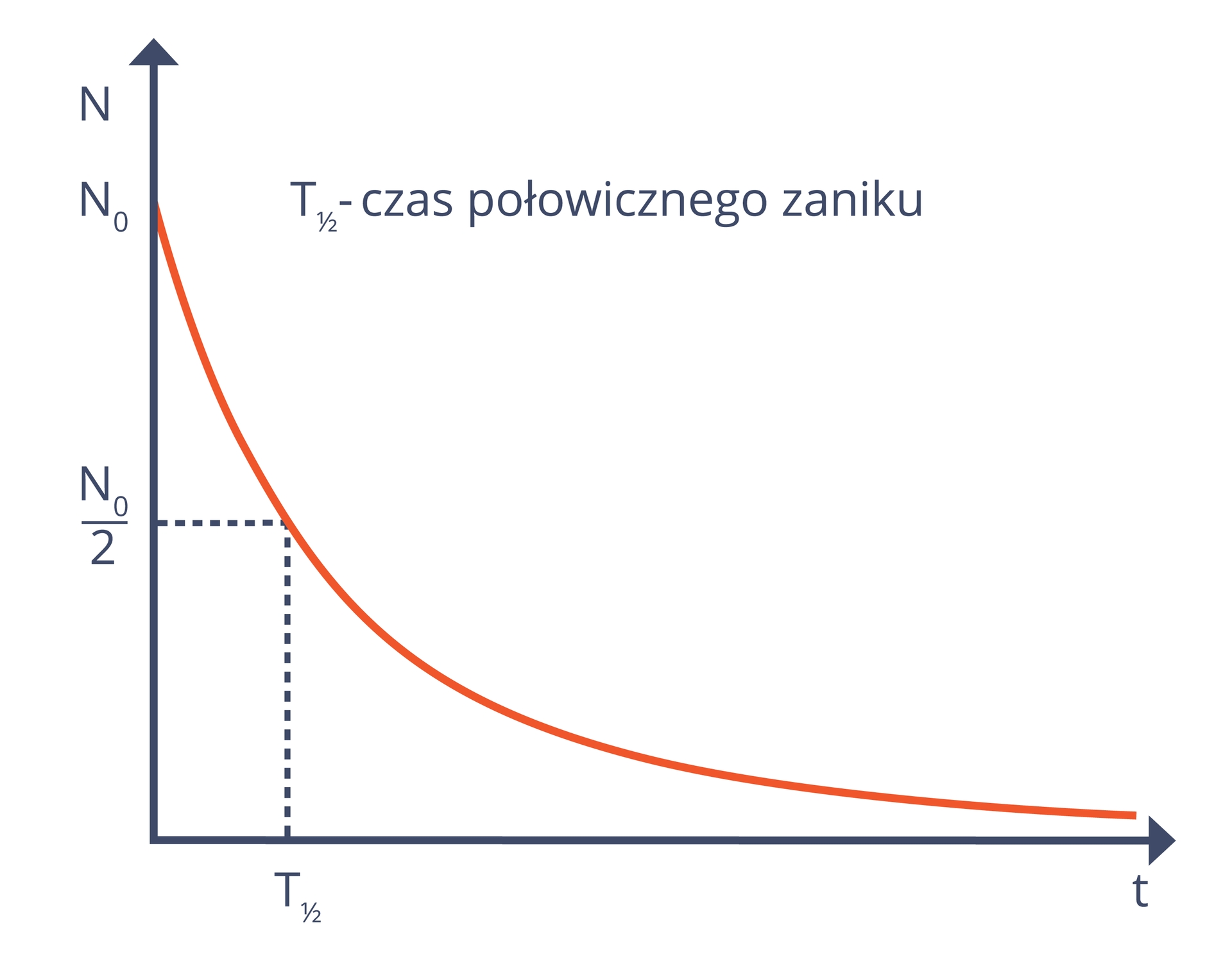
Czas, po upływie którego w próbce pozostała połowa początkowej liczby jąder, to okresem połowicznego rozpaduokres połowicznego rozpaduokresem połowicznego rozpadu (niekiedy nazywany okresem połowicznego zaniku). Czas połowicznego zaniku oznaczamy jako „ $T_{1 / 2}$ ” lub po prostu „ $T$ ”. Po upływie czasu równego dwóm okresom połowicznego zaniku zostaje $1 / 4$ jąder w stosunku do ich liczby początkowej, po trzech okresach połowicznego zaniku – $1 / 8$ itd.

Czas połowicznego rozpadu wybranych źródeł promieniotwórczych
Źródło promieniotwórcze	Czas połowicznego rozpadu $(T_{1 / 2})$	Rodzaj rozpadu
${}_{86}^{222}{Rn}$	$3,82$ dni	$α$
${}_{6}^{14}C$	$5730$ lat	$β$
${}_{53}^{131}J$	$8,1$ dni	$β$
${}_{92}^{235}U$	$7,1 \cdot 10^{8}$ lat	$α$
${}_{90}^{232}{Th}$	$1,4 \cdot 10^{10}$ lat	$α$

Czas połowicznego zaniku jąder atomów jest różny dla różnych izotopów. Może być równy zarówno bilionowym częściom sekundy, jak i miliardom lat.

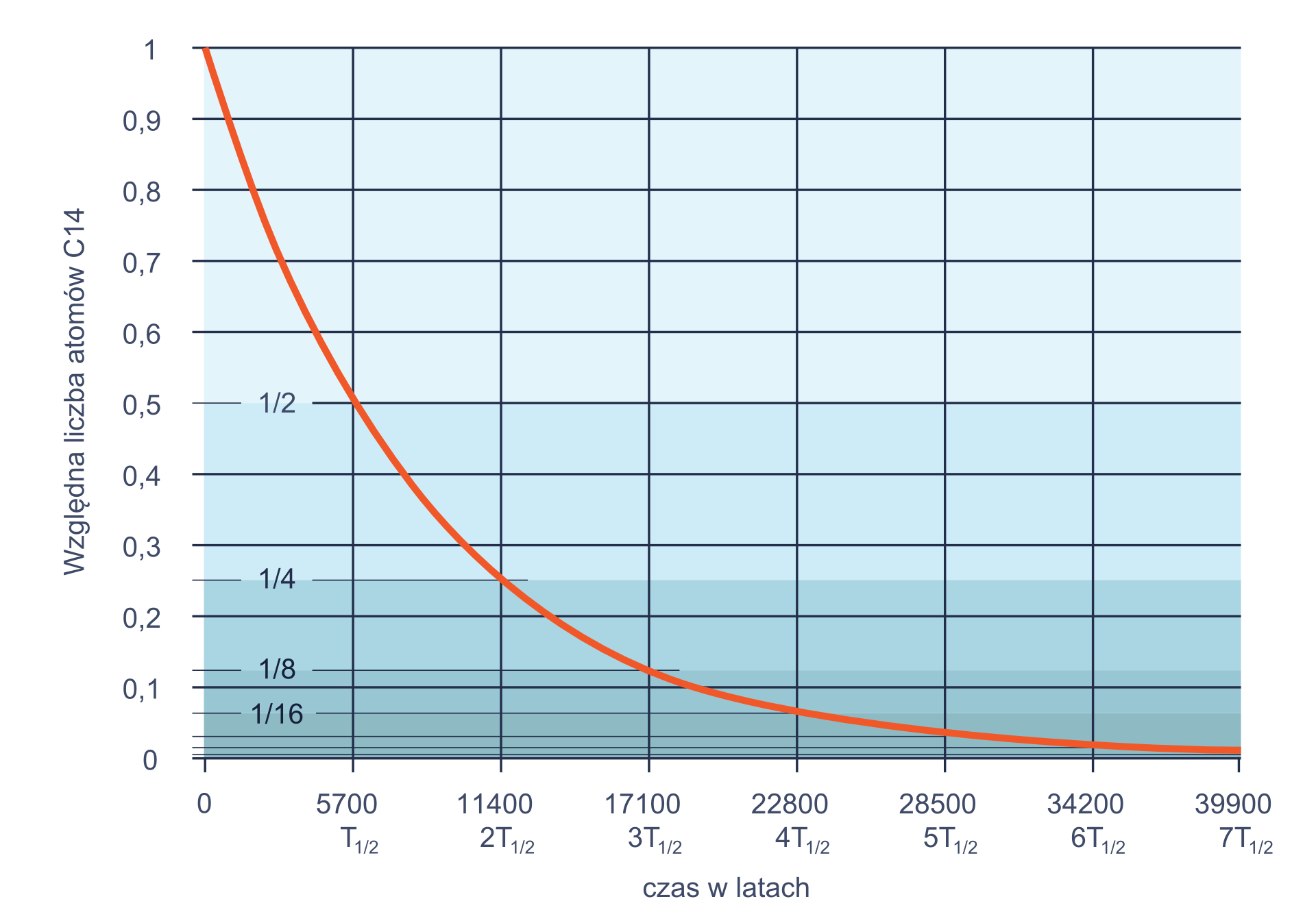
W naukach takich jak historia, archeologia, biologia i geologia ważną rolę odgrywa nietrwały izotop węgla ${}^{14}C$ , którego czas połowicznego zaniku wynosi 5730 lat. Izotop węgla ${}^{14}C$ stanowi niewielką domieszkę całej zawartości atomów węgla w materii i jeśli zmierzymy zawartość tego izotopu w danym organizmie lub przedmiocie, możemy oszacować datę powstania przedmiotu bądź śmierci organizmu.

Polecenie 2

Okres połowicznego zaniku pewnego izotopu wynosi 4 godziny. Uzupełnij poniższą tabelkę.

Rozpad izotopu promieniotwórczego w funkcji czasu
Czas [h]	$0$	$4$	$8$	$12$	$16$	$20$	$24$	$28$
Liczba jąder	$6,4 \cdot 10^{10}$

Narysuj wykres zależności liczby jąder, które uległy rozpadowi, od czasu trwania rozpadu dla tego izotopu.

Wyprowadzenie dokładnej zależności liczby jąder od czasu wymaga wiedzy na poziomie matematyki wyższej. Ale jeśli skorzystamy z pojęcia okresu połowicznego zaniku, to możemy otrzymać taką zależność w prosty sposób. Zapisz, jaka część początkowej liczby jąder pozostanie po upływie kolejnych okresów.
Na początku było $N_{0}$ , potem kolejno: $\frac{N_{0}}{2}$ , $\frac{N_{0}}{4}$ , $\frac{N_{0}}{8}$ , $\frac{N_{0}}{16}$ , $\frac{N_{0}}{32}$ . Jak zapewne zauważyliście, możemy ten ciąg zapisać jako: $N_{0}$ , $\frac{N_{0}}{2^{1}}$ , $\frac{N_{0}}{2^{2}}$ , $\frac{N_{0}}{2^{3}}$ , $\frac{N_{0}}{2^{4}}$ , $\frac{N_{0}}{2^{5}}$ , a to z kolei da się uprościć do postaci (biorąc pod uwagę, ile okresów połowicznego zaniku upłynęło):

$N = \frac{N_{0}}{2^{n}}$ ,

gdzie $n$ jest liczbą okresów połowicznego zaniku, które upłynęły od momentu rozpoczęcia procesu. Oczywiście:

n = \frac{t}{T_{1 / 2}}

i ostatecznie:

N (t) = N_{0} ∙ 2^{- \frac{t}{T_{1 / 2}}}

Ostatnia zależność pozwoli na obliczenie liczby jąder w dowolnym czasie. Potrzebne do tego będą kalkulator naukowy albo arkusz kalkulacyjny.

R1dRxZTtgFkVp1

Prawo rozpadu promieniotwórczego — Rozpad promieniotwórczy izotopu węgla ${}^{14}C$

Polecenie 3

Uzasadnij, dlaczego zamiast $N$ i $N_{0}$ nie można używać mas próbek $m (t)$ i $m_{0}$ .

Polecenie 4

Czas połowicznego zaniku pewnego pierwiastka wynosi 110 minut. Wykaż, że po 330 minutach pozostanie w tej próbce 12,5% jąder tego pierwiastka (w stosunku do stanu początkowego). Czy masa końcowa całej próbki będzie stanowiła 12,5% początkowej masy tej próbki? Dlaczego?

i7e8cV1qjf_d5e343

2. Reguły przesunięć

Pierwiastki, które emitują promieniowanie jądrowe $α$ i $β$ , ulegają przemianom jądrowym, co prowadzi do zamiany tych pierwiastków w inne pierwiastki, o czym mówi reguła przesunięć.

Na początku 1913 r. kilku fizyków (w tym Polak Kazimierz Fajans pracujący w Niemczech) sformułowało tzw.regułę przesunięćreguła przesunięćregułę przesunięć, określaną obecnie mianem reguły przesunięć Soddy’ego‑Fajansa. Podczas rozpadu $α$ przybiera ona poniższą postać:

{}_{Z}^{A}X \to {}_{2}^{4}{α + {}_{Z - 2}^{A - 4}Y}

Kiedy jądro pierwiastka X emituje cząstkę $α$ , przekształca się w jądro pierwiastka $Y$ , który ma o dwa ładunki dodatnie w jądrze mniej w porównaniu z pierwiastkiem X. Oznacza to, że nowy pierwiastek w stosunku do wyjściowego jest przesunięty o dwa miejsca w stronę mniejszych liczb porządkowych, a o cztery zmniejsza się jego liczba masowa.

W przypadku rozpadu $β$ następuje zwiększenie ładunku jądra, a nowy pierwiastek jest przesunięty o jedno miejsce w stronę większych liczb porządkowych:

${}_{Z}^{A}X \to {}_{- 1}^{0}{β + {}_{Z + 1}^{A}Y}$ ,

Zapis ${}_{- 1}^{0}β$ oznacza cząstkę o praktycznie (w stosunku do masy nukleonów) zerowej masie i ładunku ujemnym.

Co właściwie dzieje się w jądrze atomowym podczasrozpadu βi7e8cV1qjf_d655e198rozpadu β?

Ciekawostka

Neutrino to jedna z najbardziej tajemniczych cząstek elementarnych. Nie ma ładunku elektrycznego, a masa spoczynkowa tej cząstki jest bliska zeru. Oddziałuje wyjątkowo słabo z materią. Neutrina można rejestrować tylko pośrednio, na podstawie obserwacji rezultatów oddziaływań tych cząstek z jądrami atomów. Gdy neutrino zostanie wychwycone przez jądro, co statystycznie jest bardzo mało prawdopodobne, ulega rozpadowi, którego efekty możemy zaobserwować w specjalnych detektorach.

Ciekawostka

Istnienie neutrin teoretycznie przewidział PauliWolfgang PauliPauli w 1930 r. Podcza analizy rozkładu energii elektronów w rozpadzie beta, stwierdził, że w tym procesie często brakuje znacznej części początkowej wartości energii. Jak zapewne pamiętasz, w fizyce obowiązuje zasada zachowania energii: suma energii ciał w układzie przed procesem musi równać się sumie ich energii po zakończeniu procesu. W 1930 r. uważano, że w rozpadzie beta nie była spełniona zasada zachowania energii albo że istniała jeszcze jedna, trudno wykrywalna cząstka, która unosiła ze sobą część początkowej energii układu.

Eksperymentalne potwierdzenie hipotezy Pauliego o istnieniu neutrina nastąpiło dopiero w 1956 r.

RwHB61AVhJU6t1

Szereg promieniotwórczy uranowo-radowy. Czasami nowo powstałe jądro jest niestabilne i ulega kolejnym rozpadom tak długo, dopóki w efekcie przemian nie powstanie jądro stabilne

Reguły przesunięć wyjaśniły wiele niezrozumiałych dotąd zjawisk, obserwowanych podczas badania właściwości różnych pierwiastków. Jednak dopiero odkrycie neutronu ostatecznie rozwiązało zagadkę istnieniaizotopówizotopizotopów.

Warto podkreślić, że w powyższych równaniach przemian jądrowych obowiązują dwie zasady. Jedna to znana już wcześniejzasada zachowania ładunkuzasada zachowania ładunkuzasada zachowania ładunku. Zarówno w rozpadzie $α$ , jak i $β$ suma ładunków przed rozpadem jest równa sumie ładunków cząstek po rozpadzie. Drugą zasadę sformułujemy jako zasadę zachowania liczby nukleonów.

Przykład 1

Rad ${}_{88}^{226}{Ra}$ ulega rozpadowi $α$ . Schemat rozpadu jest następujący:

{}_{88}^{226}{Ra} \to {}_{2}^{4}{He + {}_{86}^{222}{Rn}}

Skorzystaliśmy tu z obu wymienionych wyżej zasad: suma ładunków przed rozpadem jest równa $88$ , suma po rozpadzie również wynosi $86 + 2 = 88$ . Suma nukleonów po rozpadzie to $4 + 222 = 226,$ czyli tyle samo co przez rozpadem.

Przykład 2

Jeden z izotopów kobaltu ${}_{27}^{60}{Co}$ emituje cząstki $β$ . Zapis rozpadu jest następujący:

{}_{27}^{60}{Co} \to {}_{- 1}^{0}{β + {}_{28}^{60}Y}

Liczba nukleonów jest stała i wynosi $60$ , suma ładunków przed rozpadem wynosi $27$ i tyle samo po rozpadzie: $- 1 + 28 = 27$ .

Wukładzie okresowymukład okresowyukładzie okresowym sprawdzamy, że pierwiastkiem $Y$ jest nikiel.

Przykładem rozpadu, w którym powstaje pozyton, jest rozpad jednego z izotopów fosforu: ${}_{15}^{30}P \to {}_{+ 1}^{0}{β + {}_{14}^{30}{Si}}$ . Sprawdź, czy spełnione są zasady zachowania wymienione wyżej. Zapiszcie ogólny schemat takiego rozpadu.

Polecenie 5

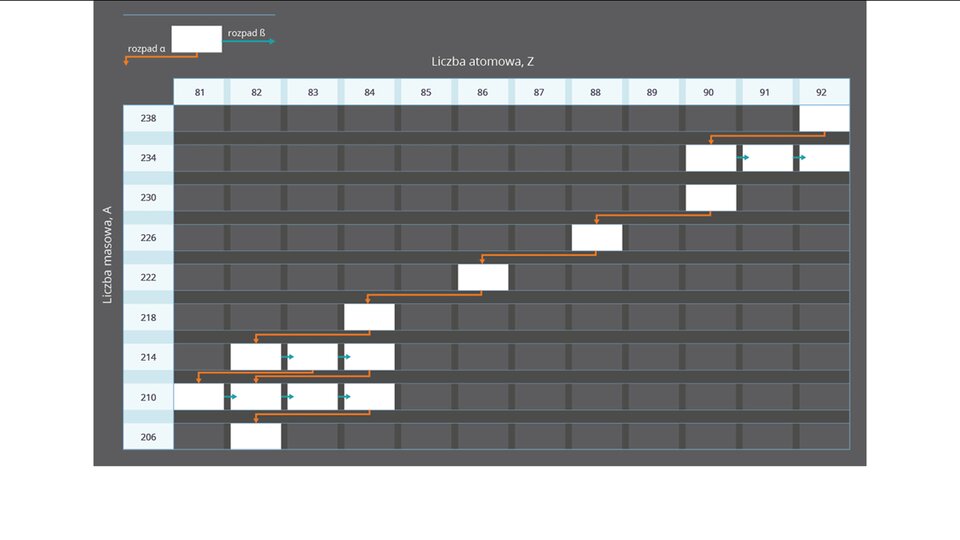
Na podstawie wykresu rozpadów dla szeregu uranowo‑radowego, zapisz kolejne rozpady, zaczynając od izotopu ${}^{238}U$ i kończąc na izotopie polonu ${}^{218}{Po}$ .

i7e8cV1qjf_d655e198

i7e8cV1qjf_d5e471

Podsumowanie

Izotopy promieniotwórcze dzielimy na stabilne (trwałe) i nietrwałe. Czas życia izotopów nietrwałych (promieniotwórczych) jest krótki, a podczas rozpadu emitują one promieniowanie $α$ , $β$ lub $γ$ .
W celu określenia stopnia radioaktywności pierwiastka wprowadzono pojęcie aktywności. Wyrażenie $A (t) = \frac{∆N}{∆t}$ nazywamy aktywnością danej próbki. Oznacza ono liczbę rozpadających się jąder w jednostce czasu (szybkość rozpadów). Aktywność ta jest proporcjonalna do aktualnej liczby jąder danego pierwiastka: $A (t) = λ \cdot N (t)$ . Ponieważ liczba jąder radioaktywnych maleje w wyniku rozpadów (a tak jest zawsze), to aktywność spada.
Jednostką aktywności promieniotwórczej jest 1 bekerel ( $Bq$ ):

1 Bq = \frac{1 rozpad}{1 s}

Aktywność promieniotwórcza jest równa jednemu bekerelowi, jeśli w czasie jednej sekundy następuje jeden rozpad promieniotwórczy.
Czas, po upływie którego w próbce pozostała połowa początkowej liczby jąder, to okres połowicznego zaniku (niekiedy nazywany również czasem połowicznego rozpadu). Oznaczamy go $T$ lub (częściej) $T_{1 / 2}$ .
Za pomocą pojęcia okresu połowicznego zaniku możemy zapisać prawo rozpadu w następującej formie:

N (t) = N_{0} \cdot 2^{- \frac{t}{T_{1 / 2}}}

R1WjG0K56MsnO1

Rozpad promieniotwórczy — Prawo rozpadu promieniotwórczego

Rozpady $α$ i $β$ podlegają regułom przesunięć (regułom Soddy’ego‑Fajansa).
Rozpad $α$ : ${}_{Z}^{A}X \to {}_{2}^{4}{α + {}_{Z - 2}^{A - 4}Y}$ .
Rozpad $β$ : ${}_{Z}^{A}X \to {}_{- 1}^{0}{β + {}_{Z + 1}^{A}Y}$ ,
Promieniowanie $γ$ (gamma) powstaje podczas rozpadów $α$ lub $β$ i jest skutkiem uwolnienia przez jądro nadmiaru energii w formie kwantów promieniowania elektromagnetycznego o bardzo dużej energii.

i7e8cV1qjf_d5e536

Zadanie podsumowujące moduł

Ćwiczenie 1

RJuJZWRYmLQ0v1

Które z poniższych stwierdzeń są prawdziwe, a które nie?

	Prawda	Fałsz
Czas połowicznego zaniku to czas, w którym rozpadnie się połowa jąder w danej próbce.	□	□
W każdym rozpadzie alfa następuje zmniejszenie się ładunku jądra.	□	□
Szybkość rozpadu promieniotwórczego to inaczej aktywność próbki.	□	□
W wyniku rozpadu beta następuje zmniejszenie się liczby protonów w jądrze.	□	□

Źródło: Dariusz Kajewski <dariusz.kajewski@up.wroc.p>, licencja: CC BY 3.0.

i7e8cV1qjf_d5e568

Praca domowa

Polecenie 6.1

Jądro powstałe w wyniku rozpadu może być dalej niestabilne i ulegać dalszym rozpadom. Jądro atomu uranu ${}_{92}^{238}U$ rozpada się tak, że powstaje jądro innego izotopu uranu ${}_{92}^{234}U$ . Jakie cząstki zostały wypromieniowane w tych rozpadach i ile ich było?

Polecenie 6.2

W przyrodzie istnieją tzw. szeregi promieniotwórcze. Dzieje się tak dlatego, że (tak jak w przykładzie powyżej) nowo powstałe jądro jest niestabilne i ulega kolejnym rozpadom tak długo, aż w efekcie przemian nie powstanie jądro stabilne. Fragment jednego z szeregów może być zapisany w następujący sposób:
${}_{88}^{226}{Ra} \to {}_{86}^{222}{Rn \to {}_{84}^{218}{Po}} \to {}_{82}^{214}{Pb \to} {}_{83}^{214}{X \to {}_{84}^{214}{Po \to}} {}_{82}^{210}{Pb \to {}_{83}^{210}{X \to {}_{84}^{210}{Po}}}$
Skorzystaj z układu okresowego i rozszyfruj pierwiastek X.

Zapisz wszystkie przejścia od jednego jądra do kolejnego i zidentyfikuj emitowaną cząstkę.

Polecenie 6.3

Odszukaj w internecie inne szeregi promieniotwórcze. Przeanalizuj ich przebieg, sprawdź, co jest produktem końcowym.

Polecenie 6.4

W czasie równym okresowi połowicznego zaniku połowa jąder ulega rozpadowi. A co stanie się w czasie połowy okresu połowicznego zaniku? W odpowiedzi wykorzystaj wykres zależności liczby jąder od czasu dla pierwiastków radioaktywnych.

i7e8cV1qjf_d5e644

Słowniczek

aktywność pierwiastka

– szybkość rozpadów promieniotwórczych izotopu obliczana jako iloraz liczby jąder ( $∆ N$ ), które uległy rozpadowi, i czasu ( $∆ t$ ), w którym ten rozpad nastąpił.

czas połowicznego rozpadu

patrz: okres połowicznego rozpaduokres połowicznego rozpaduokres połowicznego rozpadu

izotopy stabilne

– nieradioaktywne izotopy lub pierwiastki promieniotwórcze o długim czasie rozpadu.

neutrino

– cząstka niezwykle trudna do wykrycia, słabo oddziałująca z materią, obojętna elektrycznie, mająca masę spoczynkową bliską zeru; w 1930 r. istnienie neutrina przewidział Wolfgang Pauli; doświadczalne potwierdzenie istnienia tej cząstki nastąpiło dopiero w 1956 r.

okres połowicznego rozpadu (okres połowicznego zaniku)

– czas, po upływie którego w próbce pozostaje połowa początkowej liczby jąder.

reguła przesunięć

– reguła pozwalająca określić, w jaki sposób ulega zmianie liczba masowa (A) i liczba atomowa (Z) jądra izotopu przomieniotwórczego ulegają zmianie w czasie rozpadu alfa i beta.

układ okresowy

– tabela będąca zestawieniem wszystkich znanych pierwiastków chemicznych, uporządkowanych zgodnie z rosnącą wartością ich liczby atomowej.

zasada zachowania ładunku

– zasada, która wyraża doświadczalnie obserwowany fakt, że sumaryczny ładunek elektryczny układu (elektrycznie izolowanego) nie zmienia się mimo przemian, którym ten układ ulega.

zasada zachowania liczby nukleonów

– zasada mówiąca o tym, że podczas przemiany jądrowej liczba nukleonów nie ulega zmianie.

i7e8cV1qjf_d5e824

Biogram

Wolfgang Pauli

RWLpGFRGkKYcG1

Wolfgang Pauli

25.04.1900–15.12.1958

Prace Wolfganga Pauliego przyczyniły się do rozwoju mechaniki kwantowej, teorii cząstek elementarnych i kwantowej teorii pola. Fizyk postulował w 1931 r. istnienie neutrina. Największe osiągnięcie tego naukowca to bez wątpienia tzw. zakaz Pauliego – zasada opisująca sposób obsadzania stanów kwantowych w układach fermionów.

izotop1

Jądro atomowe i jego składniki

Dlaczego jądro jest trwałe – deficyt masy i energia wiązania

Przemiany jądrowe

1. Prawo rozpadu promieniotwórczego

2. Reguły przesunięć

Podsumowanie

Zadanie podsumowujące moduł

Praca domowa

Słowniczek

Biogram

Wolfgang Pauli