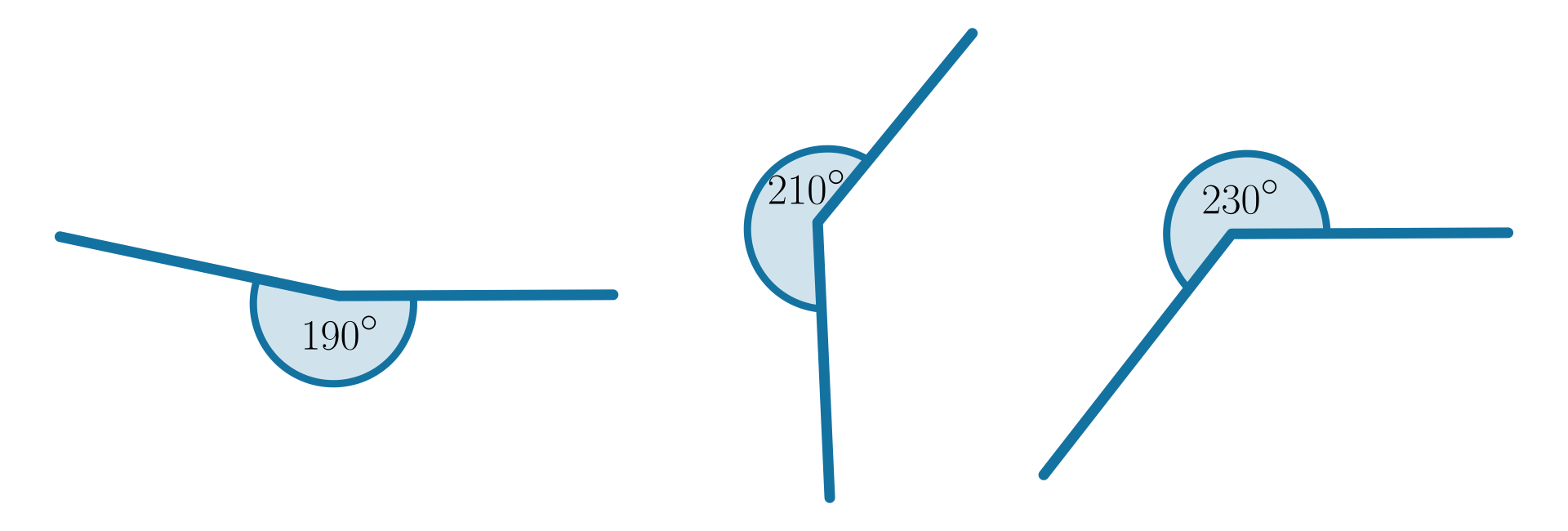R1c8xFmkB8ZSI
Ilustracja przedstawia oszklony dach budynku w kształcie trójkąta równoramiennego.

Proste, odcinki i kąty

Źródło: dostępny w internecie: hjrivas z Pixabay, domena publiczna.

4. Kąty i ich rodzaje

Z kątami mamy do czynienia nie tylko w szkolnej matematyce. Możemy dopatrzeć się wielu kątów w budynkach mieszkalnych i innych budowlach, na posadzkach i różnych ozdobach.
Kąt od dawnych czasów stosowany jest również w detalach architektonicznych, np. zwieńczających budowlę.
Od wielkości kąta zastosowanego przez projektantów zależy niekiedy bezpieczeństwo ludzi, na przykład zbyt ostry zakręt na drodze może być przyczyną wielu wypadków.

Wiemy, że niektóre ulice naszych miast mogą leżeć względem siebie prostopadle lub równoległe. A jak opisać układ ulic, które nie są do siebie ani równoległe, ani prostopadłe? Można to uczynić, korzystając z własności kątów. Co to jest kąt, z jakich elementów się składa i jakie są rodzaje kątów, dowiesz się, analizując treści zawarte w tym materiale. Zdobytą wiedzę zastosujesz, rozwiązując zamieszczone tu ćwiczenia.

Kąt
Definicja: Kąt

Dwie półproste o wspólnym początku rozcinają płaszczyznę na dwie części. Każdą z tych części, wraz z tymi półprostymi, nazywamy kątem.

Wierzchołek kąta
Definicja: Wierzchołek kąta

Wierzchołkiem kąta nazywamy wspólny początek obu półprostych, a każdą z  półprostych nazywamy ramieniem kąta.

Przykład 1

Zapoznaj się z animacją  przedstawiającą elementy budowy kąta.

R18fA6CgZK6QL1
Animacja przedstawiająca elementy budowy kąta.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Film dostępny pod adresem /preview/resource/R18fA6CgZK6QL

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Animacja przedstawiająca elementy budowy kąta.

Ważne!

  • W kącie wyróżniamy: wierzchołek kąta, ramiona kąta oraz wnętrze kąta.

  • Ramiona kąta to dwie półproste o wspólnym początku.

  • Wierzchołek kąta to punkt.

Rodzaje kątów

Zapoznaj się z poniższą animacją przedstawiającą rodzaje kątów.

R1b2jguuJTLuo
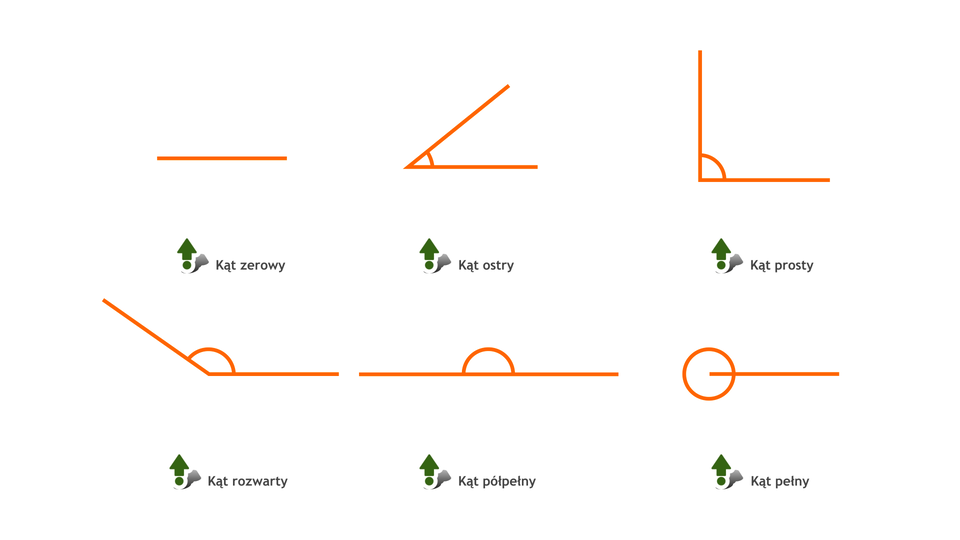
Animacja przedstawia wszystkie możliwe rodzaje kątów.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Film dostępny pod adresem /preview/resource/R1b2jguuJTLuo

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Animacja przedstawia wszystkie możliwe rodzaje kątów.

Ważne!

Kąt zerowy, ostry, prosty, rozwarty i półpełny to kąty wypukłe. Kąt, którego miara jest większa od 180° i mniejsza od 360° to kąt wklęsły.

1
R7Ft3GAwvHsmC
Grafika prezentująca możliwe rodzaje kątów.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

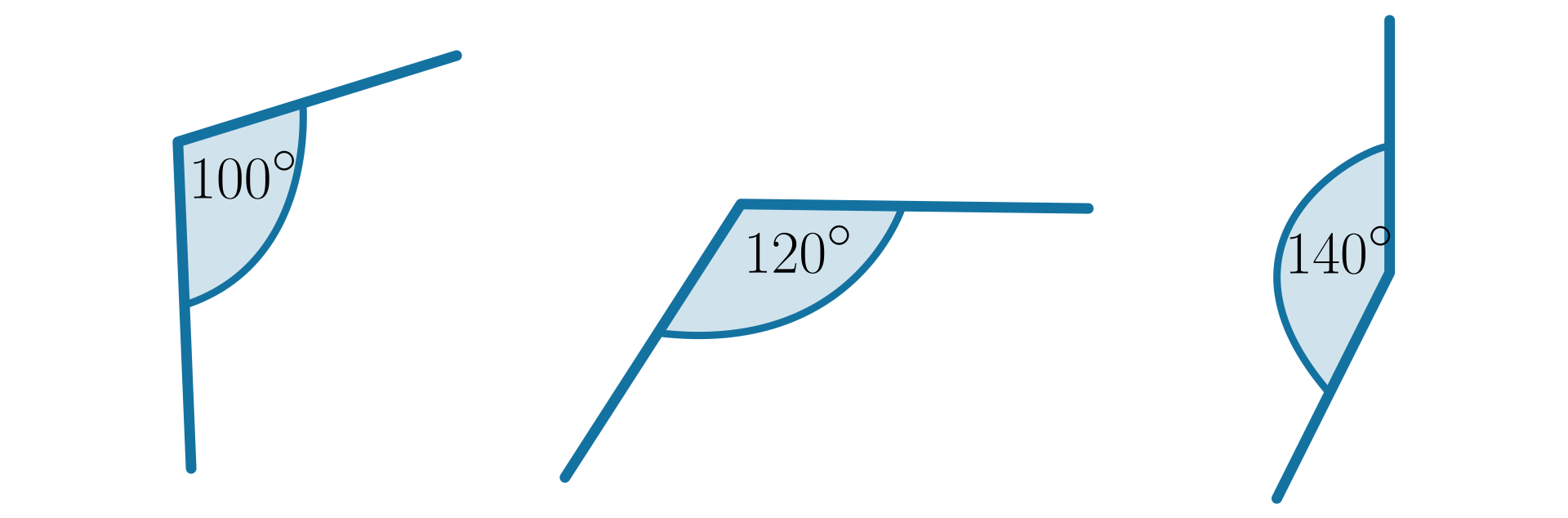
Ilustracja przedstawia podział kątów. Kąty dzielimy na:

  • zerowe, czyli takie, które mają miarę 0 stopni,

  • ostre, czyli takie, które mają miarę większą niż 0 stopni i mniejszą niż 90 stopni,

  • proste, czyli takie, które mają miarę 90 stopni,

  • rozwarte, czyli takie, które mają miarę większą niż 90 stopni i mniejszą niż 180 stopni,

  • półpełne, czyli takie, które mają miarę 180 stopni,

  • wklęsłe, czyli takie, które mają miarę większą niż 180 stopni i mniejszą niż 360 stopni,

  • pełne, czyli takie, które mają miarę 360 stopni.

Podsumujmy informacje o rodzajach kątów ze wskazaniem przykładów z naszego ortoczenia.

R1BrYaIfCCwVN1
Animacja przedstawia podstawowe rodzaje kątów.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Film dostępny pod adresem /preview/resource/R1BrYaIfCCwVN

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Animacja przedstawia podstawowe rodzaje kątów.

Rózne rodzaje kątów wystepują w architekturze i sztuce.

Już wiesz
R1MkzuBp7bkN61
Animacja pokazuje, że z różnymi rodzajami kątów spotykamy się w życiu codziennym. Możemy je zaobserwować na przykład w architekturze miast.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Film dostępny pod adresem /preview/resource/R1MkzuBp7bkN6

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Animacja pokazuje, że z różnymi rodzajami kątów spotykamy się w życiu codziennym. Możemy je zaobserwować na przykład w architekturze miast.

Przykład 2

Zapoznaj się z animacją przedstawiającą porównywanie kątów.

R8nO7kqmkL5wl1
Animacja przedstawia w jaki sposób możemy porównać ze sobą dwa kąty.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Film dostępny pod adresem /preview/resource/R8nO7kqmkL5wl

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Animacja przedstawia w jaki sposób możemy porównać ze sobą dwa kąty.

R3xmNre0Zki5T
Ćwiczenie 1
Uzupełnij podpisy elementów kąta na poniższej ilustracji. Przeciągnij odpowiednie słowa w brakujące luki.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1CmmQU5Ygvah
Ćwiczenie 1
Zaznacz wszystkie elementy kąta. Możliwe odpowiedzi: 1. ramię kąta, 2. wierzchołek kąta, 3. podstawa kąta, 4. przekątna kąta, 5. miara kąta
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RTbn2n72WrNKa1
Ćwiczenie 2
Uzupełnij definicję kąta i jego opis. 1. Dwie półproste o wspólnym początku podzieliły płaszczyznę na dwa obszary. Jeden z tych obszarów wraz z półprostymi nazywamy 1. miarę, 2. ramiona, 3. wierzchołek, 4. dowolne, 5. BC@@BA, 6. kątem, 7. CBA, 8. łukiem, 9. BA@@BC.
2. W kącie ABC: półproste 1. miarę, 2. ramiona, 3. wierzchołek, 4. dowolne, 5. BC@@BA, 6. kątem, 7. CBA, 8. łukiem, 9. BA@@BC i 1. miarę, 2. ramiona, 3. wierzchołek, 4. dowolne, 5. BC@@BA, 6. kątem, 7. CBA, 8. łukiem, 9. BA@@BC to 1. miarę, 2. ramiona, 3. wierzchołek, 4. dowolne, 5. BC@@BA, 6. kątem, 7. CBA, 8. łukiem, 9. BA@@BC kąta.
3. Punkt B, czyli wspólny początek półprostych, to 1. miarę, 2. ramiona, 3. wierzchołek, 4. dowolne, 5. BC@@BA, 6. kątem, 7. CBA, 8. łukiem, 9. BA@@BC kąta.
4. Kąt ABC można też nazwać kątem 1. miarę, 2. ramiona, 3. wierzchołek, 4. dowolne, 5. BC@@BA, 6. kątem, 7. CBA, 8. łukiem, 9. BA@@BC.
5. Kąt ABC zaznaczono na rysunku 1. miarę, 2. ramiona, 3. wierzchołek, 4. dowolne, 5. BC@@BA, 6. kątem, 7. CBA, 8. łukiem, 9. BA@@BC Punkty A i C to 1. miarę, 2. ramiona, 3. wierzchołek, 4. dowolne, 5. BC@@BA, 6. kątem, 7. CBA, 8. łukiem, 9. BA@@BC punkty leżące na ramionach kąta.
6. Symbolem ∡ABC oznaczamy 1. miarę, 2. ramiona, 3. wierzchołek, 4. dowolne, 5. BC@@BA, 6. kątem, 7. CBA, 8. łukiem, 9. BA@@BC kąta.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 3
Rip3TSbjbUFll
Określi rodzaj poniższych kątów, a następnie przeciągnij i upuść odpowiednie nazwy kątów na grafikę.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R13Qz6lzTq2rK
Uzupełnij zdania, przeciągając w luki odpowiednie opisy kątów lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. Kąty o mierze do 90° nazywamy kątami 1. pełnymi, 2. półpełnymi, 3. ostrymi, 4. wklęsłymi, 5. prostymi, 6. rozwartymi.Kąty o mierze 90° nazywamy kątami 1. pełnymi, 2. półpełnymi, 3. ostrymi, 4. wklęsłymi, 5. prostymi, 6. rozwartymi.Kąty o mierze od 90° do 180° nazywamy kątami 1. pełnymi, 2. półpełnymi, 3. ostrymi, 4. wklęsłymi, 5. prostymi, 6. rozwartymi.Kąty o mierze 180° nazywamy kątami 1. pełnymi, 2. półpełnymi, 3. ostrymi, 4. wklęsłymi, 5. prostymi, 6. rozwartymi.Kąty o mierze od 180° do 360° nazywamy kątami 1. pełnymi, 2. półpełnymi, 3. ostrymi, 4. wklęsłymi, 5. prostymi, 6. rozwartymi.Kąty o mierze 360° nazywamy kątami 1. pełnymi, 2. półpełnymi, 3. ostrymi, 4. wklęsłymi, 5. prostymi, 6. rozwartymi.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1alwxsvn7iAP1
Ćwiczenie 4
Przyjrzyj się kątom narysowanym na kwadratowej siatce. Czy potrafisz bez mierzenia kątów, nie używając kątomierza, stwierdzić, ile mają stopni? Połącz opisy odpowiednich kątów z odpowiadającymi im grafikami.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Rzdbf1nyVXWHV
Ćwiczenie 4
ostry Możliwe odpowiedzi: 1. 189°, 2. 136°, 3. 234°, 4. 16°, 5. 58°, 6. 158°, 7. 179°, 8. 345°, 9. 45° rozwarty Możliwe odpowiedzi: 1. 189°, 2. 136°, 3. 234°, 4. 16°, 5. 58°, 6. 158°, 7. 179°, 8. 345°, 9. 45° wklęsły Możliwe odpowiedzi: 1. 189°, 2. 136°, 3. 234°, 4. 16°, 5. 58°, 6. 158°, 7. 179°, 8. 345°, 9. 45°
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
1
Ćwiczenie 5

Przesuwając punkt B, ustaw tak ramię kąta BSA, aby miara tego kąta była równa podanej wartości. Skorzystaj z kątomierza.

R1MOsavrqb7eG1
Animacja pokazuje kąt B S A. Zmieniając położenie jednego z ramion kąta, należy przy użyciu kątomierza, skonstruować nowy kąt B S A o podanej mierze.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/D6L0DLUy8

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R12jJLV00U3dm
Ułóż w odpowiedniej kolejności etapy rysowania kąta za pomocą kątomierza. Kliknij w lukę, aby rozwinąć listę i wybrać prawidłową odpowiedź.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RB1ZLXphrUjgE
Ćwiczenie 6
Uzupełnij zdania, przeciągając w luki odpowiednie liczby lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. Trójkąt ma wszystkie kąty wewnętrzne tej samej miary. Wynika stąd, że miara pojedynczego kąta wynosi 1. wklęsły, 2. ostry, 3. jeden, 4. rozwarty, 5. 90°, 6. trzy, 7. prostym, 8. 60°, 9. dwa, czyli jest to kąt 1. wklęsły, 2. ostry, 3. jeden, 4. rozwarty, 5. 90°, 6. trzy, 7. prostym, 8. 60°, 9. dwa.
Trójkąt prostokątny ma jeden z kątów równy mierze 1. wklęsły, 2. ostry, 3. jeden, 4. rozwarty, 5. 90°, 6. trzy, 7. prostym, 8. 60°, 9. dwa nazywany kątem1. wklęsły, 2. ostry, 3. jeden, 4. rozwarty, 5. 90°, 6. trzy, 7. prostym, 8. 60°, 9. dwa.
Trójkąt zbudowany z kątów 120°, 20° oraz 40° zawiera 1. wklęsły, 2. ostry, 3. jeden, 4. rozwarty, 5. 90°, 6. trzy, 7. prostym, 8. 60°, 9. dwa kąty ostre i kąt 1. wklęsły, 2. ostry, 3. jeden, 4. rozwarty, 5. 90°, 6. trzy, 7. prostym, 8. 60°, 9. dwa.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 6
R1CKn6rfvxcOV
Zaznacz wszystkie kąty, które nie są kątami prostymi. Rysunek sześciu kątów o różnych miarach. Pierwszy kąt ma miarę 85 stopni, drugi kąt ma miarę 25 stopni, trzeci kąt ma miarę 90 stopni, czwarty kąt ma miarę 90 stopni, piąty kąt ma miarę 30 stopni, szósty kąt ma miarę 60 stopni.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RE6QwLiwGRrhH
Zaznacz wszystkie miary kątów, które nie są kątami prostymi. Możliwe odpowiedzi: 1. 0°, 2. 60°, 3. 90°, 4. 180°
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 7

Narysuj kąt prosty i kąt ostry.

RZD7jdlkPEDJW
Szkicownik.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Podaj miary kąta prostego i kąta ostrego.

Ćwiczenie 8
R4cT5c1u7Vkkc
Zaznacz wszystkie kąty rozwarte. Rysunek sześciu kątów o różnych miarach. Pierwszy kąt ma miarę 90 stopni, drugi kąt ma miarę 20 stopni, trzeci kąt ma miarę 170 stopni, czwarty kąt ma miarę 150 stopni, piąty kąt ma miarę 140 stopni, szósty kąt ma miarę 90 stopni.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RnI6Ov29ZnoVC
Zaznacz wszystkie miary kątów, które są kątami rozwartymi. Możliwe odpowiedzi: 1. 100°, 2. 120°, 3. 170°, 4. 30°, 5. 90°, 6. 190°
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 9
R18JH5TPjhny91
Zadanie interaktywne.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RzqrSeFIFS3US
Przeciągnij i upuść w pustą lukę lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej nazwę kąta odpowiednią do jego miary. Kąt o mierze 120° to kąt 1. ostry, 2. pełny, 3. prosty, 4. ostry, 5. rozwarty, 6. rozwarty, 7. półpełny, 8. ostry, 9. rozwarty, 10. ostry, 11. prosty, 12. półpełny, 13. pełny, 14. rozwarty.Kąt o mierze 45° to kąt 1. ostry, 2. pełny, 3. prosty, 4. ostry, 5. rozwarty, 6. rozwarty, 7. półpełny, 8. ostry, 9. rozwarty, 10. ostry, 11. prosty, 12. półpełny, 13. pełny, 14. rozwarty.Kąt o mierze 60° to kąt 1. ostry, 2. pełny, 3. prosty, 4. ostry, 5. rozwarty, 6. rozwarty, 7. półpełny, 8. ostry, 9. rozwarty, 10. ostry, 11. prosty, 12. półpełny, 13. pełny, 14. rozwarty.Kąt o mierze 90° to kąt 1. ostry, 2. pełny, 3. prosty, 4. ostry, 5. rozwarty, 6. rozwarty, 7. półpełny, 8. ostry, 9. rozwarty, 10. ostry, 11. prosty, 12. półpełny, 13. pełny, 14. rozwarty.Kąt o mierze 360° to kąt 1. ostry, 2. pełny, 3. prosty, 4. ostry, 5. rozwarty, 6. rozwarty, 7. półpełny, 8. ostry, 9. rozwarty, 10. ostry, 11. prosty, 12. półpełny, 13. pełny, 14. rozwarty.Kąt o mierze 180° to kąt 1. ostry, 2. pełny, 3. prosty, 4. ostry, 5. rozwarty, 6. rozwarty, 7. półpełny, 8. ostry, 9. rozwarty, 10. ostry, 11. prosty, 12. półpełny, 13. pełny, 14. rozwarty.Kąt o mierze 160° to kąt 1. ostry, 2. pełny, 3. prosty, 4. ostry, 5. rozwarty, 6. rozwarty, 7. półpełny, 8. ostry, 9. rozwarty, 10. ostry, 11. prosty, 12. półpełny, 13. pełny, 14. rozwarty.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 10

Narysuj trzy kąty rozwarte.

R1ZyZ3ytlV7KH
Szkicownik.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Podaj miary trzech różnych kątów rozwartych.

RwYjaWBqpoeXG
Ćwiczenie 11
Przeciągnij i upuść w pustą lukę lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej odpowiedni tekst. Kąt rozwarty jest zawsze 1. mniejszy, 2. mniejszy, 3. mniejszy, 4. większy, 5. większy, 6. większy, 7. mniejszy, 8. większy od kąta ostrego.Kąt półpełny jest zawsze 1. mniejszy, 2. mniejszy, 3. mniejszy, 4. większy, 5. większy, 6. większy, 7. mniejszy, 8. większy od kąta rozwartegoKąt prosty jest zawsze 1. mniejszy, 2. mniejszy, 3. mniejszy, 4. większy, 5. większy, 6. większy, 7. mniejszy, 8. większy od kąta ostrego i 1. mniejszy, 2. mniejszy, 3. mniejszy, 4. większy, 5. większy, 6. większy, 7. mniejszy, 8. większy od kąta rozwartego.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 12
R2k5FSuUInXaG
Zaznacz kąty wklęsłe. Rysunek sześciu kątów o różnych miarach. Pierwszy kąt o mierze 90 stopni, drugi kąt o mierze 300 stopni, trzeci kąt o mierze 140 stopni, czwarty kąt o mierze 185 stopni, piąty kąt o mierze 180 stopni, szósty kąt o mierze 270 stopni.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RINVmwA9EjtAe
Zaznacz wszystkie miary kątów, które są kątami wklęsłymi. Możliwe odpowiedzi: 1. 250°, 2. 310°, 3. 190°, 4. 170°, 5. 360°, 6. 150°
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 13

Narysuj trzy kąty wklęsłe.

RKT4ihEDDWe8e
Szkicownik.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Podaj miary trzech różnych kątów wklęsłych.

1
Ćwiczenie 14

Uruchom aplet i postępuj zgodnie z poleceniem, określając rodzaj kąta PQR.

RQVSFRS9xmPsC1
Animacja pokazuje kąt P Q R. Należy dla różnych miar kątów podać jego rodzaj.

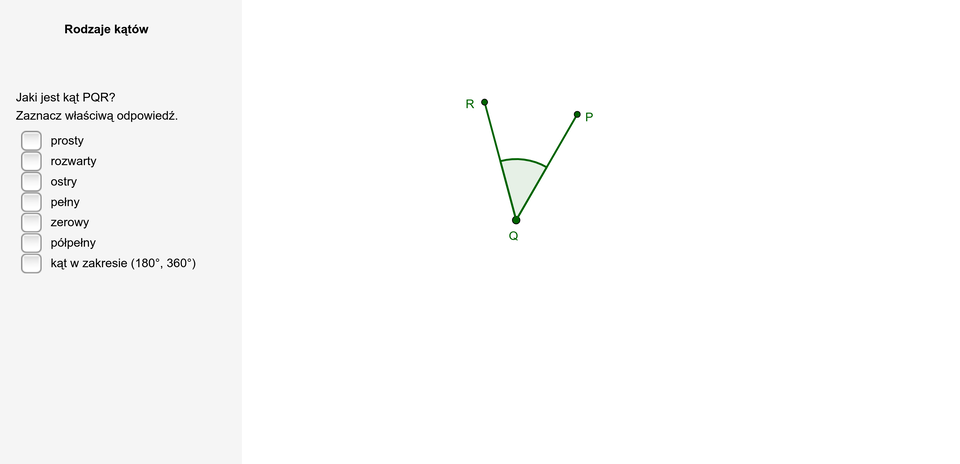
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/D6L0DLUy8

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RJuJOjalshVuv
Przeciągnij i upuść w pustą lukę lub kliknij w lukę i wybierz z listy rozwijalnej nazwę kąta odpowiednią do jego miary. Kąt o mierze 30° to kąt 1. rozwarty, 2. półpełny, 3. rozwarty, 4. półpełny, 5. wklęsły, 6. pełny, 7. ostry, 8. prosty, 9. pełny, 10. zerowy, 11. rozwarty.Kąt o mierze 110° to kąt 1. rozwarty, 2. półpełny, 3. rozwarty, 4. półpełny, 5. wklęsły, 6. pełny, 7. ostry, 8. prosty, 9. pełny, 10. zerowy, 11. rozwarty.Kąt o mierze 360° to kąt 1. rozwarty, 2. półpełny, 3. rozwarty, 4. półpełny, 5. wklęsły, 6. pełny, 7. ostry, 8. prosty, 9. pełny, 10. zerowy, 11. rozwarty.Kąt o mierze 0° to kąt 1. rozwarty, 2. półpełny, 3. rozwarty, 4. półpełny, 5. wklęsły, 6. pełny, 7. ostry, 8. prosty, 9. pełny, 10. zerowy, 11. rozwarty.Kąt o mierze 180° to kąt 1. rozwarty, 2. półpełny, 3. rozwarty, 4. półpełny, 5. wklęsły, 6. pełny, 7. ostry, 8. prosty, 9. pełny, 10. zerowy, 11. rozwarty.Kąt o mierze 200° to kąt 1. rozwarty, 2. półpełny, 3. rozwarty, 4. półpełny, 5. wklęsły, 6. pełny, 7. ostry, 8. prosty, 9. pełny, 10. zerowy, 11. rozwarty.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 15
R6SUN937nD7mA
Przeciągnij w luki na rysunku odpowiednie nazwy elementów oznaczonych na grafice.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R15ItI4SbmmLx
Jak nazywamy wspólny początek dwóch półprostych, które tworzą kąt? Zaznacz poprawną odpowiedź. Możliwe odpowiedzi: 1. Wierzchołek, 2. Ramię, 3. Wnętrze kąta
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 16
R1auNmaOY8f3I
Przeciągnij w luki na rysunku odpowiednie nazwy elementów oznaczonych na grafice.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1bycWQRkPLri
Jak nazywamy półproste, z których składa się kąt? Zaznacz poprawną odpowiedź. Możliwe odpowiedzi: 1. Ramiona, 2. Wierzchołki, 3. Wnętrza kąta
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 17

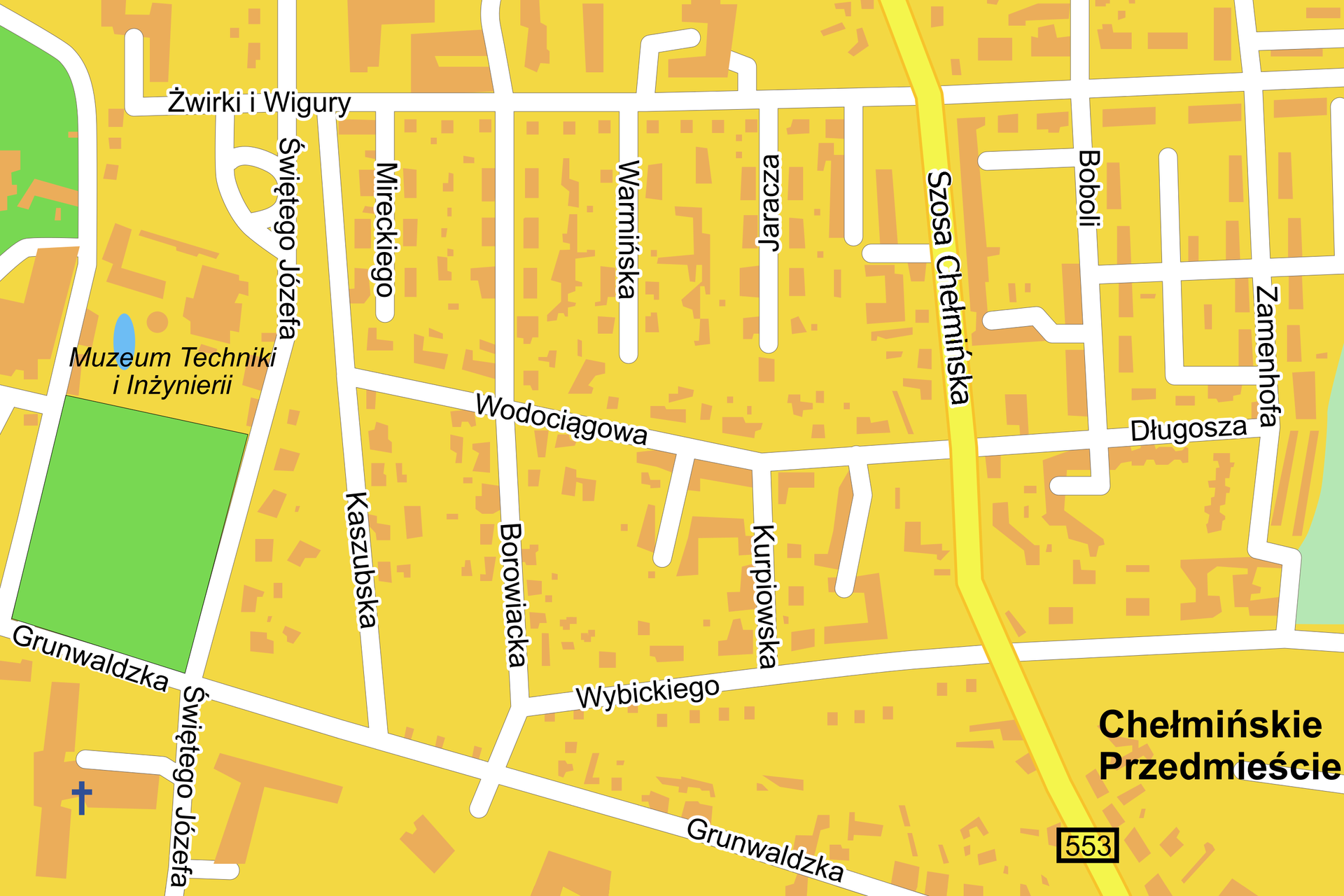
Oto fragment planu Torunia.

RfVbPvPdsu2UX1
Fragment planu Torunia.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1Hl6eBmwMaC8
Zaznacz wszystkie zdania prawdziwe. Możliwe odpowiedzi: 1. Ulice Borowiecka i Wybickiego przecinają się pod kątem ostrym., 2. Ulice Wodociągowa i Wigury przecinają się pod kątem rozwartym., 3. Ulice Wodociągowa i Kurpiowska przecinają się pod kątem rozwartym., 4. Ulice Zamenhofa i Długosza przecinają się pod kątem prostym.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RoafYkR0BspLI
Zaznacz wszystkie zdania prawdziwe. Możliwe odpowiedzi: 1. Ulice Wodociągowa i Kaszubska przecinają się pod kątem większym niż 90° i mniejszym niż 180°, czyli przecinają się pod kątem ostrym., 2. Ulice Zamenhofa i Długosza przecinają się pod kątem prostym, czyli przecinają się pod katem 90°., 3. Ulice Borowiecka i Wybickiego przecinają się pod kątem większym niż 0° i mniejszym niż 90°, czyli przecinają się pod kątem ostrym., 4. Ulice Wodociągowa i Kurpiowska przecinają się pod kątem większym niż 90° i mniejszym niż 180°, czyli przecinają się pod kątem rozwartym.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R3CdWqbxZ2jjM1
Ćwiczenie 18
Jaki kąt: ostry, prosty, rozwarty, półpełny, wklęsły czy pełny zakreśla wskazówka minutowa pomiędzy podanymi godzinami. Przeciągnij w luki odpowiednią nazwę kąta lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. Wskazówka minutowa pomiędzy godziną 10:00, a 10:25 zakreśla kąt 1. półpełny, 2. półpełny, 3. półpełny, 4. pełny, 5. prosty, 6. prosty, 7. prosty, 8. wklęsły, 9. prosty, 10. rozwarty, 11. rozwarty, 12. wklęsły, 13. półpełny, 14. wklęsły, 15. ostry, 16. rozwarty, 17. ostry, 18. ostry, 19. rozwarty, 20. ostry, 21. rozwarty, 22. półpełny, 23. półpełny, 24. wklęsły, 25. pełny, 26. wklęsły, 27. prosty, 28. prosty, 29. pełny, 30. pełny, 31. wklęsły, 32. ostry, 33. pełny, 34. pełny, 35. rozwarty, 36. ostry.
Wskazówka minutowa pomiędzy godziną 16:15, a 16:46 zakreśla kąt 1. półpełny, 2. półpełny, 3. półpełny, 4. pełny, 5. prosty, 6. prosty, 7. prosty, 8. wklęsły, 9. prosty, 10. rozwarty, 11. rozwarty, 12. wklęsły, 13. półpełny, 14. wklęsły, 15. ostry, 16. rozwarty, 17. ostry, 18. ostry, 19. rozwarty, 20. ostry, 21. rozwarty, 22. półpełny, 23. półpełny, 24. wklęsły, 25. pełny, 26. wklęsły, 27. prosty, 28. prosty, 29. pełny, 30. pełny, 31. wklęsły, 32. ostry, 33. pełny, 34. pełny, 35. rozwarty, 36. ostry.
Wskazówka minutowa pomiędzy godziną 18:47, a 19:02 zakreśla kąt 1. półpełny, 2. półpełny, 3. półpełny, 4. pełny, 5. prosty, 6. prosty, 7. prosty, 8. wklęsły, 9. prosty, 10. rozwarty, 11. rozwarty, 12. wklęsły, 13. półpełny, 14. wklęsły, 15. ostry, 16. rozwarty, 17. ostry, 18. ostry, 19. rozwarty, 20. ostry, 21. rozwarty, 22. półpełny, 23. półpełny, 24. wklęsły, 25. pełny, 26. wklęsły, 27. prosty, 28. prosty, 29. pełny, 30. pełny, 31. wklęsły, 32. ostry, 33. pełny, 34. pełny, 35. rozwarty, 36. ostry.
Wskazówka minutowa pomiędzy godziną 22:45, a 23:31 zakreśla kąt 1. półpełny, 2. półpełny, 3. półpełny, 4. pełny, 5. prosty, 6. prosty, 7. prosty, 8. wklęsły, 9. prosty, 10. rozwarty, 11. rozwarty, 12. wklęsły, 13. półpełny, 14. wklęsły, 15. ostry, 16. rozwarty, 17. ostry, 18. ostry, 19. rozwarty, 20. ostry, 21. rozwarty, 22. półpełny, 23. półpełny, 24. wklęsły, 25. pełny, 26. wklęsły, 27. prosty, 28. prosty, 29. pełny, 30. pełny, 31. wklęsły, 32. ostry, 33. pełny, 34. pełny, 35. rozwarty, 36. ostry.
Wskazówka minutowa pomiędzy godziną 05:07, a 05:37 zakreśla kąt 1. półpełny, 2. półpełny, 3. półpełny, 4. pełny, 5. prosty, 6. prosty, 7. prosty, 8. wklęsły, 9. prosty, 10. rozwarty, 11. rozwarty, 12. wklęsły, 13. półpełny, 14. wklęsły, 15. ostry, 16. rozwarty, 17. ostry, 18. ostry, 19. rozwarty, 20. ostry, 21. rozwarty, 22. półpełny, 23. półpełny, 24. wklęsły, 25. pełny, 26. wklęsły, 27. prosty, 28. prosty, 29. pełny, 30. pełny, 31. wklęsły, 32. ostry, 33. pełny, 34. pełny, 35. rozwarty, 36. ostry.
Wskazówka minutowa pomiędzy godziną 15:16, a 16:16 zakreśla kąt 1. półpełny, 2. półpełny, 3. półpełny, 4. pełny, 5. prosty, 6. prosty, 7. prosty, 8. wklęsły, 9. prosty, 10. rozwarty, 11. rozwarty, 12. wklęsły, 13. półpełny, 14. wklęsły, 15. ostry, 16. rozwarty, 17. ostry, 18. ostry, 19. rozwarty, 20. ostry, 21. rozwarty, 22. półpełny, 23. półpełny, 24. wklęsły, 25. pełny, 26. wklęsły, 27. prosty, 28. prosty, 29. pełny, 30. pełny, 31. wklęsły, 32. ostry, 33. pełny, 34. pełny, 35. rozwarty, 36. ostry.

Jaki kąt: ostry, prosty, rozwarty, półpełny, wklęsły czy pełny zakreśla wskazówka minutowa pomiędzy godzinami

ostry, wklęsły, rozwarty, pełny, rozwarty, rozwarty, wklęsły, ostry, ostry, półpełny, pełny, półpełny, rozwarty, pełny, półpełny, ostry, prosty, półpełny, wklęsły, prosty, pełny, ostry, pełny, wklęsły, wklęsły, ostry, rozwarty, prosty, rozwarty, półpełny, półpełny, wklęsły, pełny, prosty, prosty, prosty

a) 10:00, a 10:25? ......................
b) 16:15, a 16:46? ......................
c) 18:47, a 19:02? ......................
d) 22:45, a 23:31? ......................
e) 5:07, a 5:37? ......................
e)15:16, a 16:16? ......................

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RFInfrabY9KKB1
Ćwiczenie 19
Jaki kąt: ostry, prosty, rozwarty, półpełny, wklęsły, czy pełny zakreśla wskazówka minutowa pomiędzy podanymi godzinami. Przeciągnij w luki odpowiednią nazwę kąta lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. Wskazówka minutowa pomiędzy godziną 7:28, a 8:28 zakreśla kąt 1. wklęsły, 2. pełny, 3. pełny, 4. prosty, 5. półpełny, 6. prosty, 7. rozwarty, 8. ostry, 9. półpełny, 10. półpełny, 11. ostry, 12. prosty, 13. rozwarty, 14. prosty, 15. rozwarty, 16. wklęsły, 17. rozwarty, 18. ostry, 19. wklęsły, 20. pełny, 21. wklęsły, 22. prosty, 23. półpełny, 24. pełny, 25. rozwarty, 26. ostry, 27. pełny, 28. ostry, 29. półpełny, 30. wklęsły.
Wskazówka minutowa pomiędzy godziną 9:11, a 9:12 zakreśla kąt 1. wklęsły, 2. pełny, 3. pełny, 4. prosty, 5. półpełny, 6. prosty, 7. rozwarty, 8. ostry, 9. półpełny, 10. półpełny, 11. ostry, 12. prosty, 13. rozwarty, 14. prosty, 15. rozwarty, 16. wklęsły, 17. rozwarty, 18. ostry, 19. wklęsły, 20. pełny, 21. wklęsły, 22. prosty, 23. półpełny, 24. pełny, 25. rozwarty, 26. ostry, 27. pełny, 28. ostry, 29. półpełny, 30. wklęsły.
Wskazówka minutowa pomiędzy godziną 12:35, a 13:24 zakreśla kąt 1. wklęsły, 2. pełny, 3. pełny, 4. prosty, 5. półpełny, 6. prosty, 7. rozwarty, 8. ostry, 9. półpełny, 10. półpełny, 11. ostry, 12. prosty, 13. rozwarty, 14. prosty, 15. rozwarty, 16. wklęsły, 17. rozwarty, 18. ostry, 19. wklęsły, 20. pełny, 21. wklęsły, 22. prosty, 23. półpełny, 24. pełny, 25. rozwarty, 26. ostry, 27. pełny, 28. ostry, 29. półpełny, 30. wklęsły.
Wskazówka minutowa pomiędzy godziną 14:15, a 14:30 zakreśla kąt 1. wklęsły, 2. pełny, 3. pełny, 4. prosty, 5. półpełny, 6. prosty, 7. rozwarty, 8. ostry, 9. półpełny, 10. półpełny, 11. ostry, 12. prosty, 13. rozwarty, 14. prosty, 15. rozwarty, 16. wklęsły, 17. rozwarty, 18. ostry, 19. wklęsły, 20. pełny, 21. wklęsły, 22. prosty, 23. półpełny, 24. pełny, 25. rozwarty, 26. ostry, 27. pełny, 28. ostry, 29. półpełny, 30. wklęsły.
Wskazówka minutowa pomiędzy godziną 17:48, a 18:18 zakreśla kąt 1. wklęsły, 2. pełny, 3. pełny, 4. prosty, 5. półpełny, 6. prosty, 7. rozwarty, 8. ostry, 9. półpełny, 10. półpełny, 11. ostry, 12. prosty, 13. rozwarty, 14. prosty, 15. rozwarty, 16. wklęsły, 17. rozwarty, 18. ostry, 19. wklęsły, 20. pełny, 21. wklęsły, 22. prosty, 23. półpełny, 24. pełny, 25. rozwarty, 26. ostry, 27. pełny, 28. ostry, 29. półpełny, 30. wklęsły.

Jaki kąt: ostry, prosty, rozwarty, półpełny, wklęsły, czy pełny zakreśla wskazówka minutowa pomiędzy godzinami

wklęsły, wklęsły, rozwarty, ostry, wklęsły, prosty, pełny, prosty, ostry, półpełny, pełny, półpełny, półpełny, ostry, ostry, rozwarty, pełny, prosty, ostry, rozwarty, półpełny, pełny, prosty, rozwarty, półpełny, prosty, pełny, wklęsły, rozwarty, wklęsły

a) 7:28, a 8:28? ......................
b) 9:11, a 9:12? ......................
c) 12:35, a 13:24? ......................
d) 14:15, a 14:30? ......................
e) 17:48, a 18:18? ......................

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Notatnik

Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.

R1b8OvSPUG8s3
(Uzupełnij).
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
3. Mierzenie odcinków
5. Mierzenie kątów