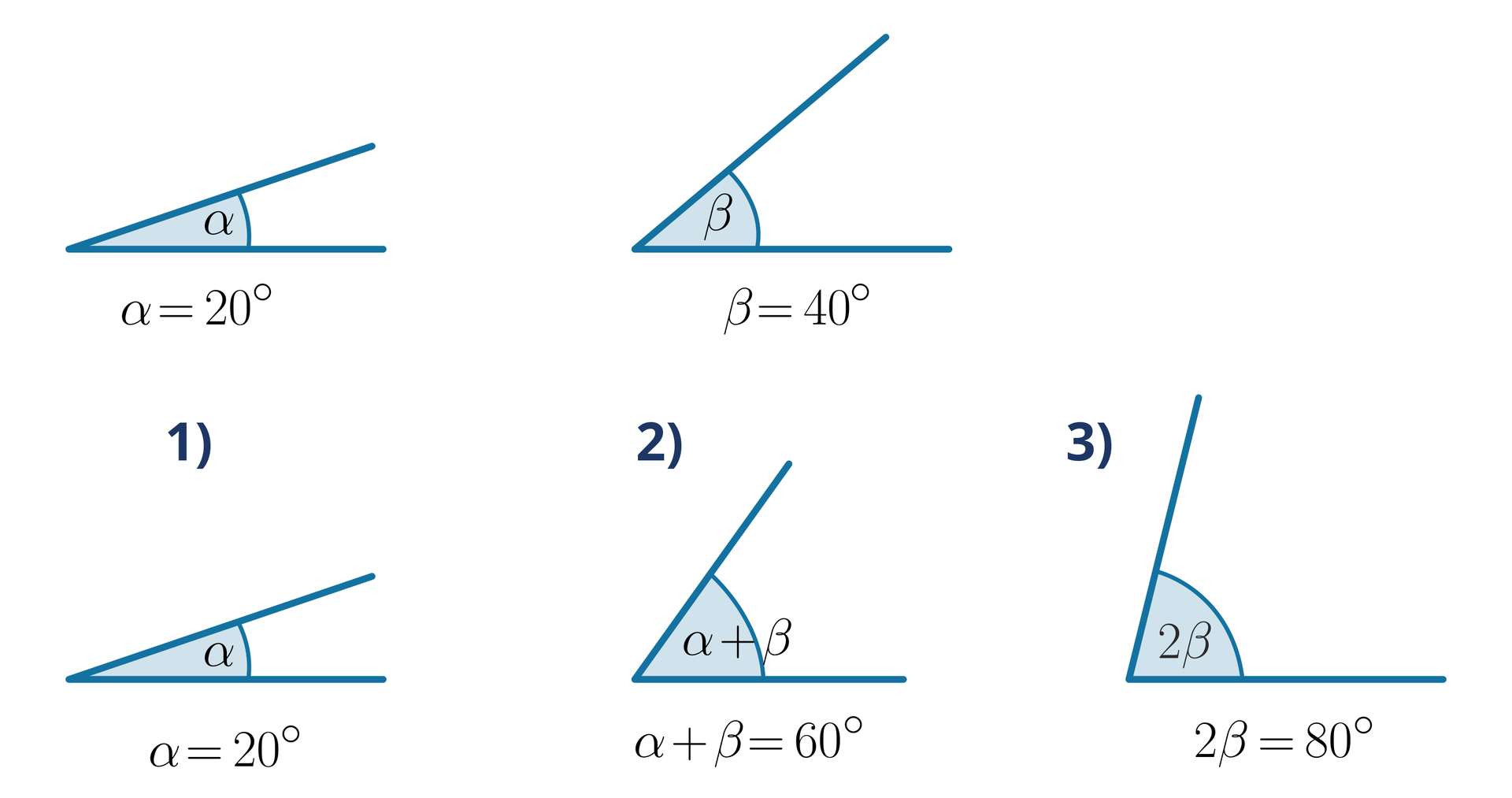Własności figur geometrycznych na płaszczyźnie
4. Przystawanie figur
Z pewnością niejednokrotnie zdarzyło Ci się zachwycać wyglądem pałacowych parkietów, na przykład takich, jak na poniższym rysunku.

Zazwyczaj można dostrzec w nich pewną regularność – w szczególności powtarzające się kształty i motywy. Są one także przedmiotem zainteresowania matematyków – to oni, aby uniknąć mówienia o układaniu parkietu, wprowadzili pojęcie parkietażu, czyli pokrycia płaszczyzny (a nawet powierzchni w przestrzeni) przylegającymi do siebie figurami (płytkami), najczęściej w kształcie wielokątów. Możemy mówić o parkietażach foremnych, gdy składają się one z wielokątów foremnych, których jednakowa liczba schodzi się w każdym wierzchołku, albo np. o parkietażach półforemnych, które składają się z różnych wielokątów foremnych o identycznych wierzchołkach.


Warto zauważyć, że można ułożyć parkiet (stworzyć parkietaż) pokrywając go motywem w kształcie dowolnego trójkąta. Wystarczy, że pierwszy z trójkątów odbijemy symetrycznie względem środka dowolnego z jego boków – powstaje wówczas równoległobok, który wystarczy odpowiednio przesuwać.

Użyte do powyższego pokrycia wielokąty są trójkątami przystającymi, które gwarantują powtarzalność i niewielką złożoność otrzymanego wzoru. Okazuje się jednak, co pokazują prace Mauritsa Cornelisa Eschera, że powtarzalność (przystawanie) jednego elementu nie musi wcale oznaczać prostoty całego ornamentu.

Analizując przykłady zawarte w tym materiale poznasz definicję, przykłady oraz własności figur przystających. Rozwiązując ćwiczenia – sprawdzisz ukształtowane umiejętności.
Figury przystające

Film dostępny pod adresem /preview/resource/R19X5vL6uJXe5
Animacja przedstawia jakie figury możemy nazywać figurami przystającymi.
Rysunek przedstawia cztery figury.
Porównaj kształty i wielkości tych figur. Co zauważasz?
Zapoznaj się z opisem poniższego apletu.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/D6YlKQGHV
Figurę zieloną, figurę czerwoną i figurę niebieską można nałożyć na figurę czarną tak, aby figury te pokrywały się.
Takie figury nazywamy przystającymi.
Figury, które mają ten sam kształt i tę samą wielkość nazywamy przystającymi.
Przykład figur przystających
R1WrhUWvH8aAx1  Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Obrazem figury w symetrii środkowej jest figura do niej przystająca.
Obrazem figury w symetrii osiowej jest figura do niej przystająca.

Film dostępny pod adresem /preview/resource/R1SGdAGx1OfZU
Animacja przedstawia jak wygląda obraz pewnej figury figury w symetrii osiowej i obraz tej figury w symetrii środkowej.
Przykłady figur przystających
Zastanówmy się, jakie długości muszą mieć promienie dwóch kół, aby te koła były przystające.
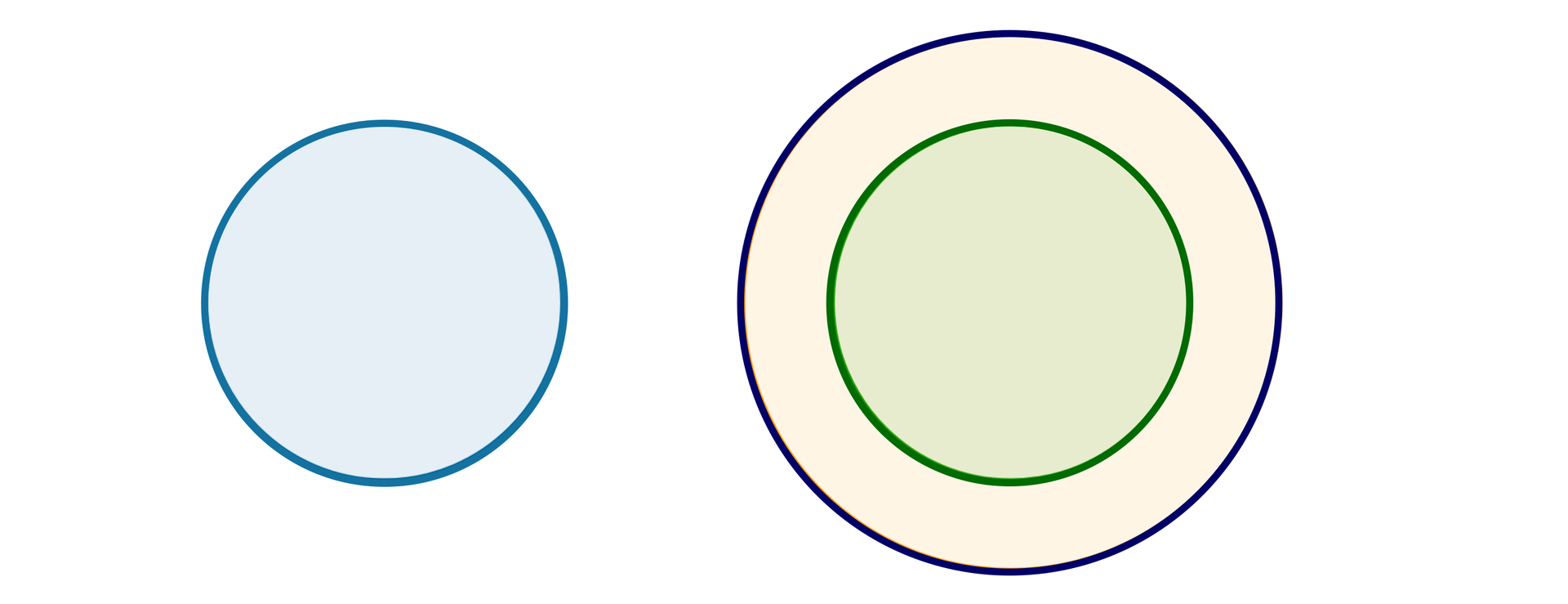
Dwa koła są przystające, jeśli mają równe promienie.
Dwa okręgi są przystające, jeśli mają równe promienie.
Na rysunku przedstawione są odcinki przystające. Zbadaj ich długości.
Wyciągnij wniosek i sformułuj warunek, jaki muszą spełniać dwa odcinki, aby były przystające.
Na rysunku przedstawione są odcinki przystające. Co można powiedzieć o ich długości? Wyciągnij wniosek i sformułuj warunek, jaki muszą spełniać dwa odcinki, aby były przystające.

Dwa odcinki są przystające wtedy i tylko wtedy, gdy mają równe długości.
Wskaż odcinki przystające.

Dwa kąty o równych miarach są przystające.
Wskaż pary kątów przystających.

Wskaż pary kątów przystających. Przyjmij, że oznacza kąt . Pierwszy kąt ma miarę , drugi kąt ma miarę , trzeci kąt ma miarę , czwarty kąt ma miarę , piąty kąt ma miarę i szósty kąt ma miarę .
Rysunki przedstawiają pary wielokątów przystających. Porównaj miary kątów i długości boków wielokątów każdej pary. Co zauważasz?

Wielokąty przystające mają odpowiadające sobie boki równej długości oraz równe miary odpowiadających sobie kątów.

Wielokąty na rysunku mają równe, odpowiadające sobie kąty. Zbadaj, czy są przystające.

Wielokąty są przystające tylko wtedy, kiedy kolejne kąty jednego wielokąta są równe kolejnym kątom drugiego, a boki położone między takimi samymi kątami w jednym i drugim wielokącie są równe.
Prostokąty i są przystające. Obwód prostokąta jest równy . Różnica długości i szerokości prostokąta jest równa . Ile wynosi pole prostokąta ?

Obwody prostokątów przystających są równe, zatem obwód prostokąta jest równy .
Oznaczmy: – szerokość prostokąta (w ), a – długość prostokąta (w ).
Zapisujemy i rozwiązujemy równanie, które pozwoli na obliczenie szerokości prostokąta .
Obliczamy długość prostokąta : .
Pole prostokąta wynosi
Pola prostokątów przystających są równe. Pole prostokąta jest więc równe .
Z figur przystających często tworzone są wzory na tapetach, posadzkach czy tkaninach.

Narysuj dwa przystające:
Opisz dwa przystające:
prostokąty,
romby,
równoległoboki.
Sformułuj warunek przystawania:
prostokątów,
kwadratów,
kół.
Wskaż pary figur przystających.

Zaproponuj sposób podziału kąta na kąty przystające.
Narysuj dowolny czworokąt. Skonstruuj odcinek równy sumie przekątnych tego czworokąta.
Dany jest pewien kwadrat. Chcemy skonstruować kwadrat do niego przystający. Czy wystarczy, że skonstruowany kwadrat będzie miał boki równe bokom podanego kwadratu?
Narysuj dwa dowolne kąty i . Skonstruuj kąt
przystający do kąta
Podaj przykład kątów i , a następnie odpowiedz na pytania:
Jaką miarę będzie miał kąt przystający do kąta ?
Jaką miarę będzie miał kąt ?
Jaką miarę będzie miał kąt ?
Narysuj dowolny siedmiokąt. Skonstruuj kąt przystający do największego kąta narysowanego siedmiokąta.
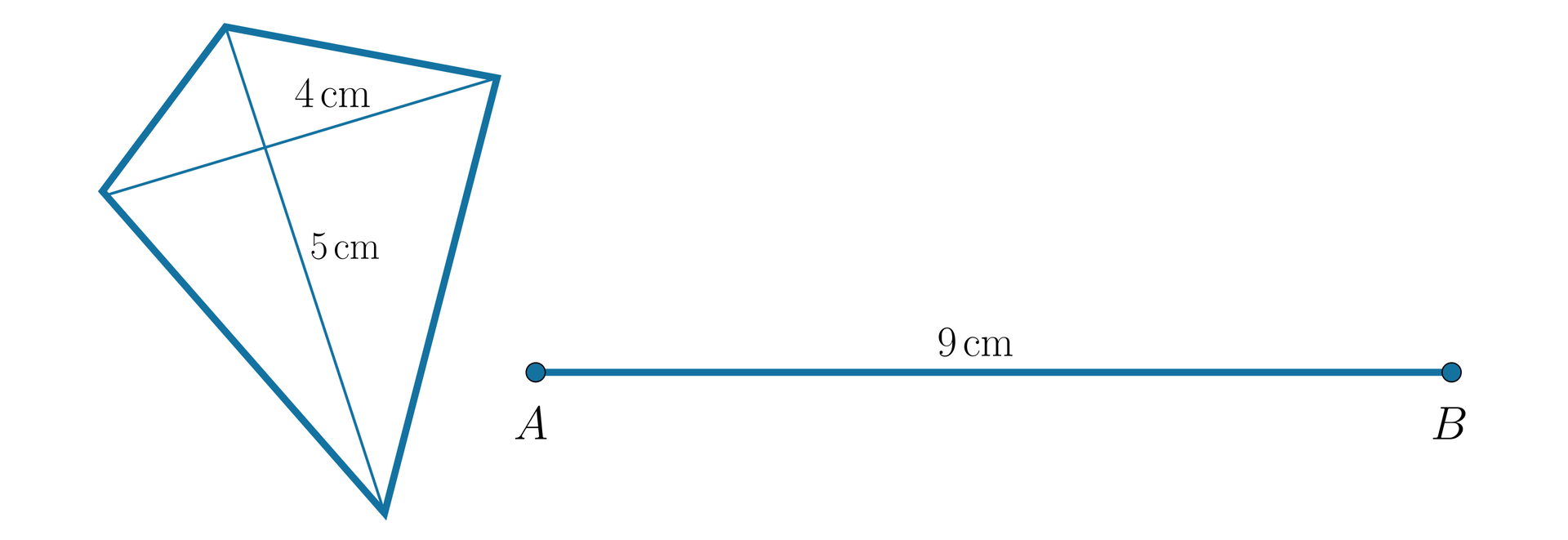
Czworokąty na rysunku są przystające. Oblicz miary ich kątów.

Narysuj trzy nieprzystające prostokąty, które mają jednakowe obwody.
Podaj wymiary trzech nieprzystających prostokątów, które mają jednakowe obwody.
Informacje do zadań 31, 32, 33
Taras w domu pana Bronka ma kształt taki, jak na rysunku. Przyjmijmy, że długość kratki jest równa .

Pan Bronek chce kupić na wyłożenie tarasu płytki terakoty w takim kształcie, aby po docięciu ich pozostało jak najmniej odpadów. Chciałby też, aby płytki miały jak największą powierzchnię. Zaproponuj, w jakim kształcie i o jakich wymiarach mogłyby być te płytki.
Notatnik
Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.