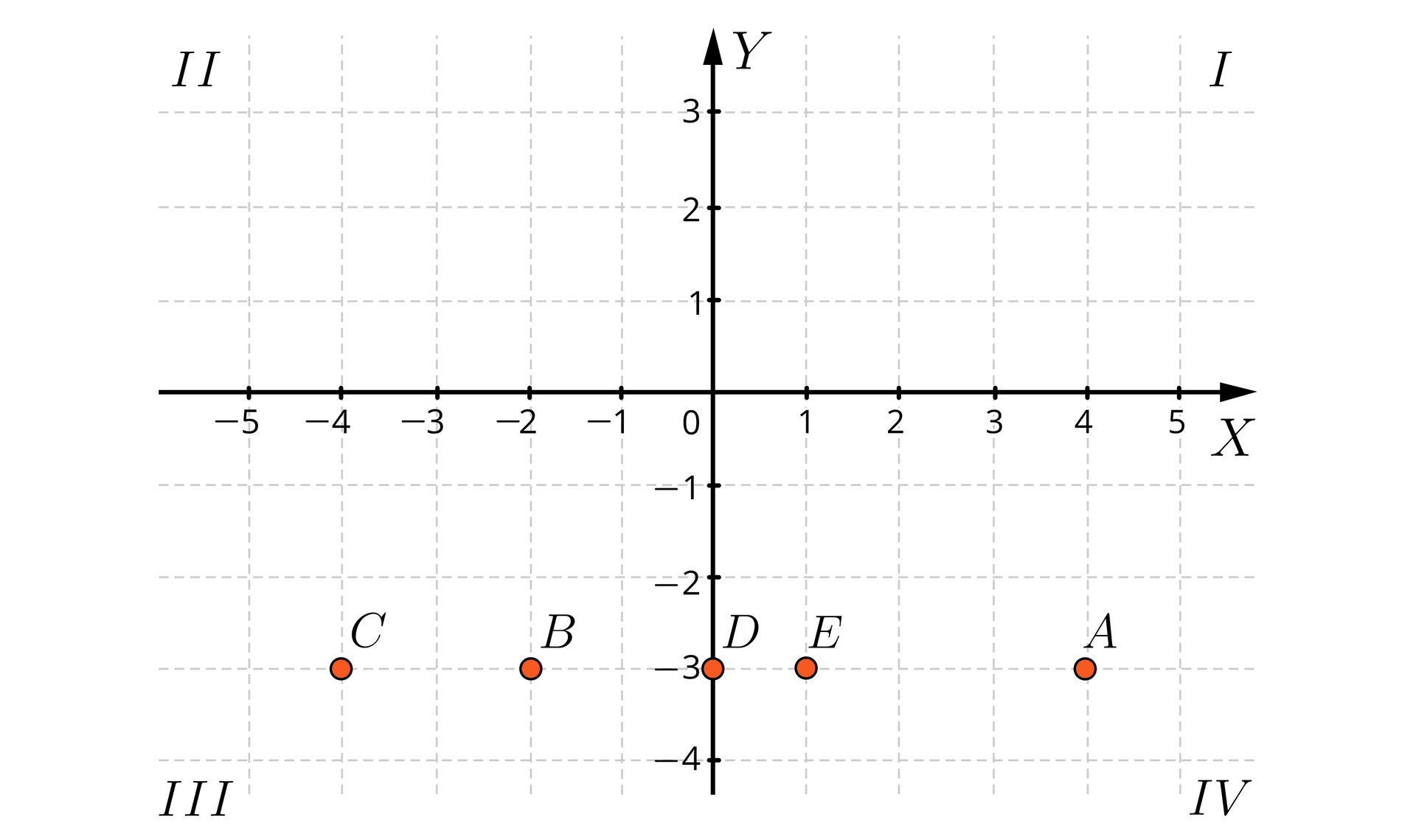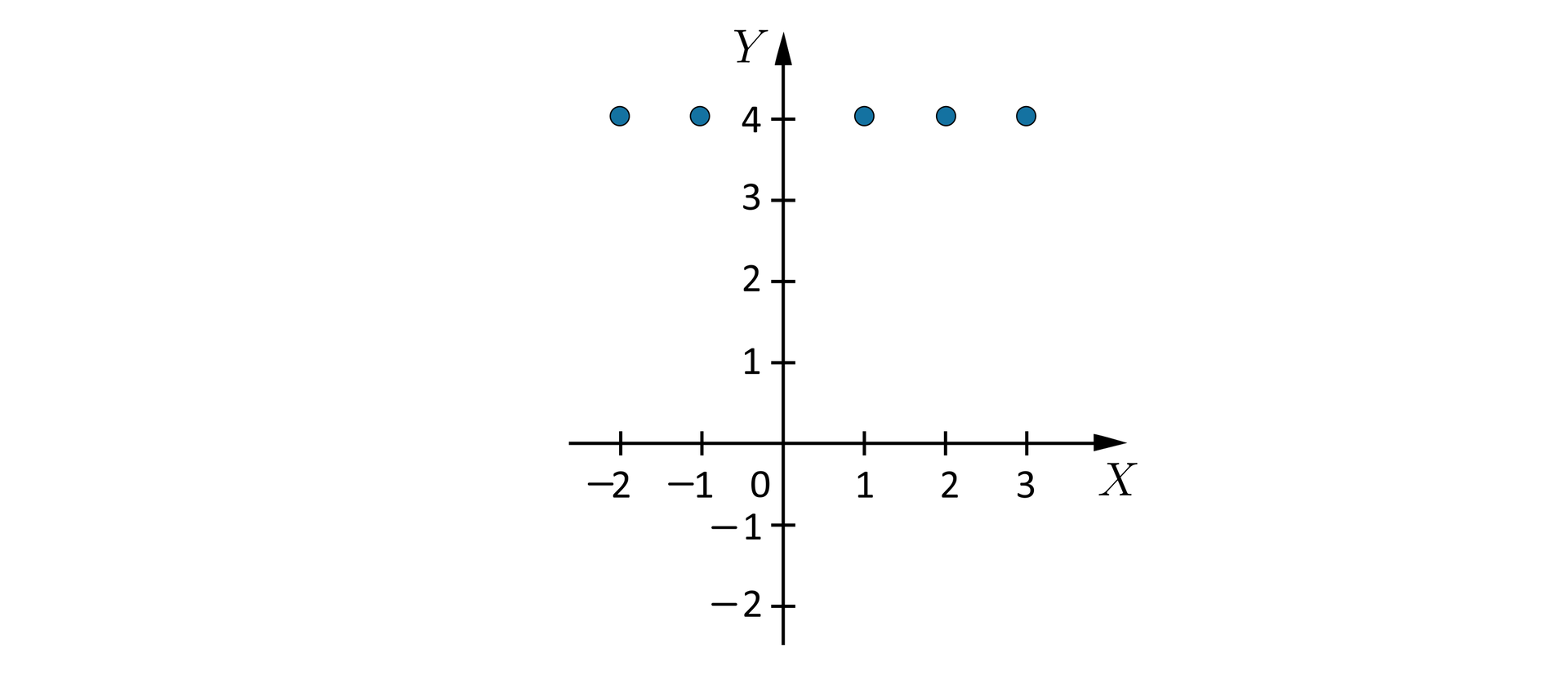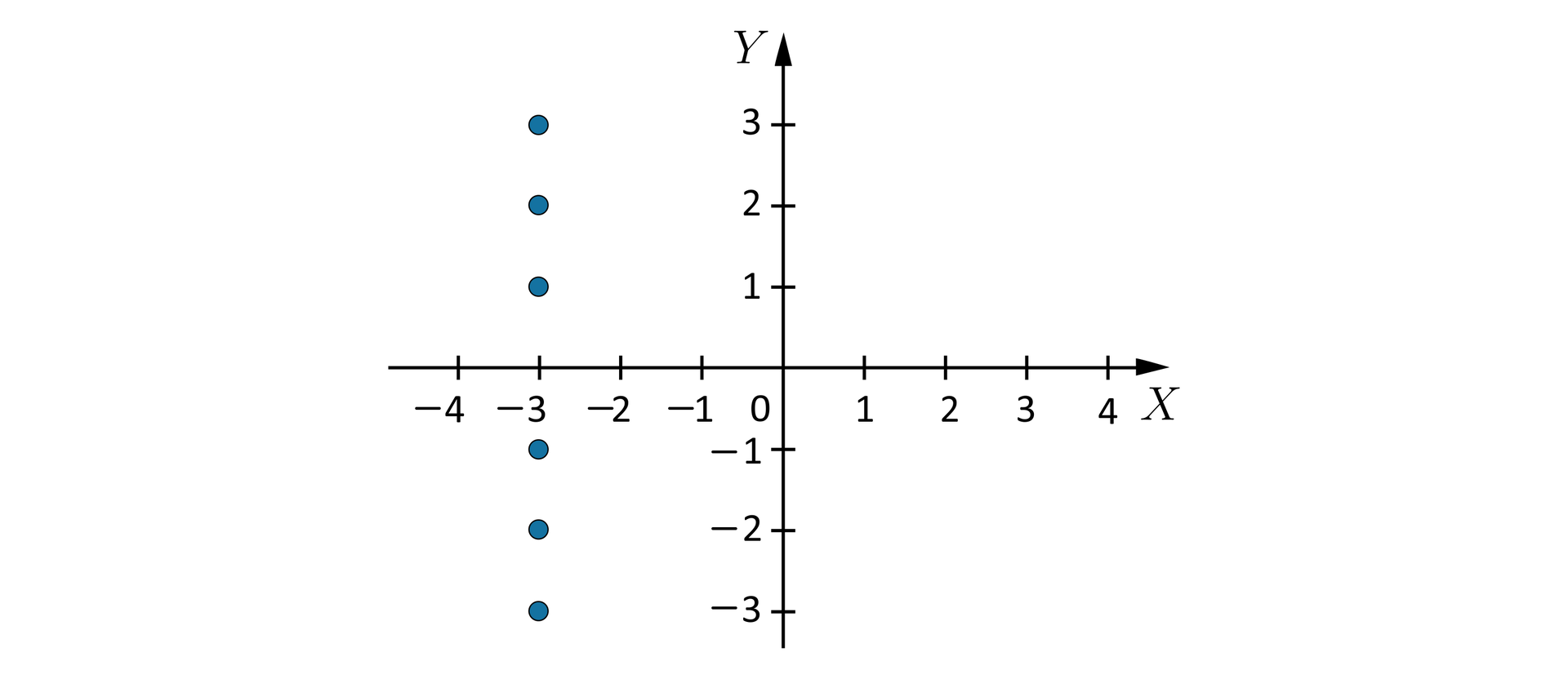Układ współrzędnych
2. Punkty kratowe w układzie współrzędnych
Podczas wpisywania haseł do naszej krzyżówki trzeba wiedzieć, gdzie wpisać pierwszą literę. Jej położenie opisano za pomocą liczby i litery, np. . Taki opis określa dokładnie położenie pola w diagramie.
Poziomo
– ,
– najmniejsza liczba trzycyfrowa,
– może być liczbowa,
– odcinek łączący sąsiednie wierzchołki wielokąta,
– figura przestrzenna.
Pionowo
– czworokąt o równych bokach,
– .
Położenie punktów na mapie
Geografowie określają położenie obiektów na kuli ziemskiej, korzystając z układu współrzędnych geograficznych, które wyznaczają południki, równoleżniki, równik i bieguny. Punkt zaznaczony na siatce geograficznej opisywany jest za pomocą pary liczb, nazywanej jego współrzędnymi geograficznymi. Pierwsza współrzędna to długość geograficzna, a druga – szerokość geograficzna. Punkt przecięcia południka zerowego z równikiem to początek układu współrzędnych.
W tej części materiału rozwiążesz zadania dotyczące położenia na mapie.
Współrzędne punktu to długości geograficznej wschodniej i szerokości geograficznej północnej.
W zapisie międzynarodowym: .
Odczytaj współrzędne geograficzne (szerokość i długość) następujących miejscowości:
Międzyrzec Podlaski,
Tarnów
Kraków

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/D91NVnRlI
Poruszając się w nieznanym terenie swoje położenie można określić posługując się np. planem okolicy. Opisz za pomocą pary uporządkowanej położenie na planie:
Wielkiego Stawu Polskiego,
Kościelca,
Opalonego Wierchu.
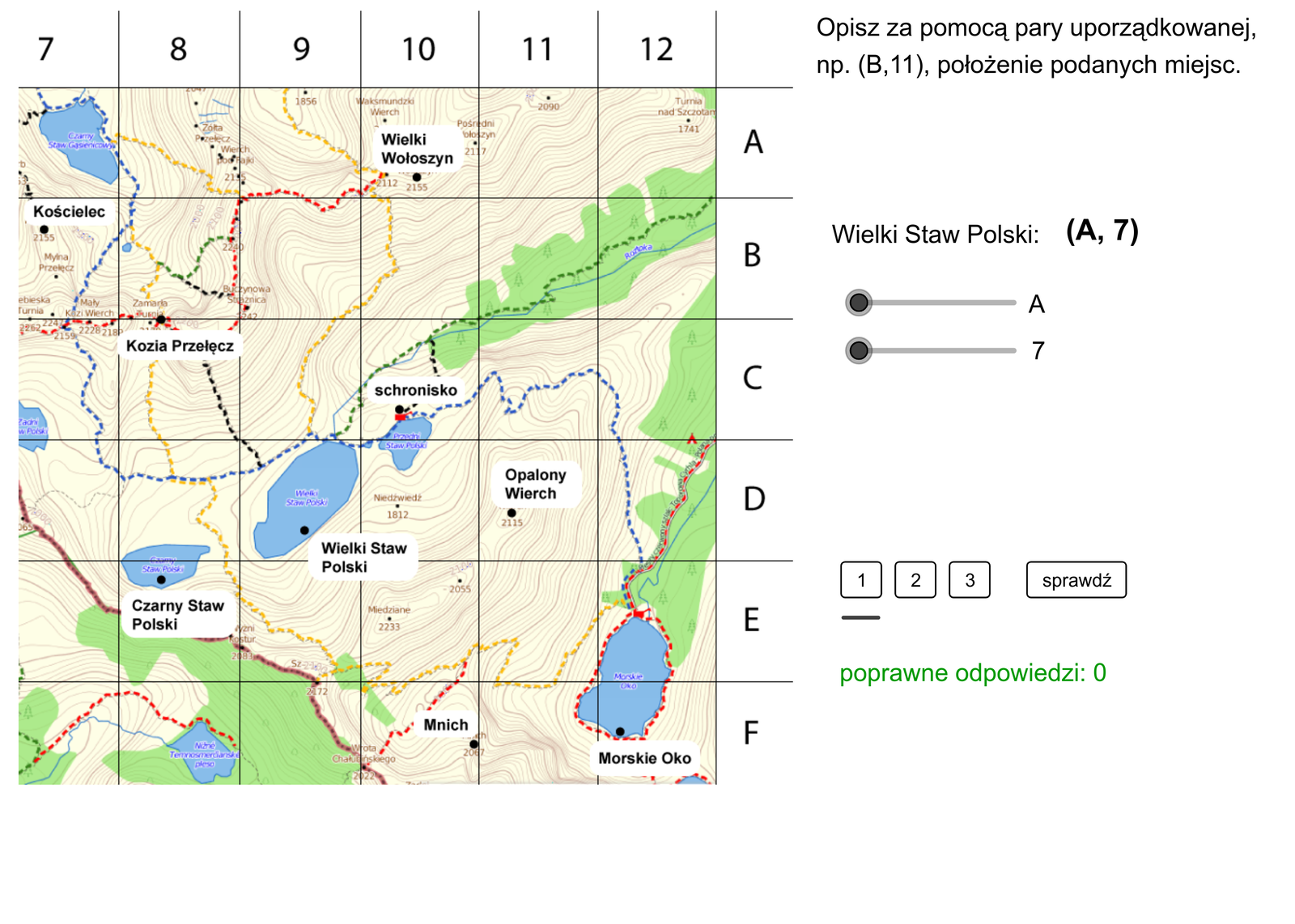
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/D91NVnRlI

2. 1. Wielki Staw Polski, 2. Kozia Przełęcz, 3. Kościelec, 4. schronisko, 5. Morskie Oko, 6. Wielki Wołoszyn, 7. Mnich, 8. Opalony Wierch, 9. Czarny Staw Polski,
3. 1. Wielki Staw Polski, 2. Kozia Przełęcz, 3. Kościelec, 4. schronisko, 5. Morskie Oko, 6. Wielki Wołoszyn, 7. Mnich, 8. Opalony Wierch, 9. Czarny Staw Polski.
W praktyce do szybkiego wyznaczania położenia obiektu (nawet poruszającego się) wykorzystuje się najczęściej Globalny System Nawigacji (GPS), który obejmuje swym zasięgiem całą kulę ziemską. System ten jest ogólnodostępny, z jego usług może korzystać każda osoba, która posiada odpowiedni odbiornik.
Układy współrzędnych stosuje się również w wielu innych dziedzinach wiedzy, np. w geodezji, fizyce (do opisywania ruchu ciał).
Kartezjański układ współrzędnych
Każdy punkt na osi liczbowej można opisać za pomocą liczby, czyli jego współrzędnej, np. , ma współrzędną .

Podobnie opisujemy położenie punktów na płaszczyźnie, ale punkty zaznaczamy w prostokątnym układzie współrzędnych.
W matematyce najczęściej posługujemy się układem współrzędnych, który tworzą dwie wzajemnie prostopadłe osie liczbowe. Punkt przecięcia tych prostych nazywany jest początkiem układu współrzędnych.

Oś pozioma (pierwsza oś) nazywana jest osią odciętych lub osią .
Oś pionowa (druga oś) nazywana jest osią rzędnych lub osią .
Prostokątny układ współrzędnych nazywany jest układem kartezjańskim od Kartezjusza (Rene Descartes’a), znakomitego siedemnastowiecznego francuskiego matematyka, przyrodnika i filozofa, którego uważa się za prekursora stosowania metod geometrycznych w zagadnieniach algebraicznych.
Powszechnie znana jest sentencja filozoficzna Kartezjusza „Myślę, więc jestem”.

Każdemu punktowi zaznaczonemu w układzie współrzędnych odpowiada uporządkowana para liczb nazywanych jego współrzędnymi.
Zapisujemy
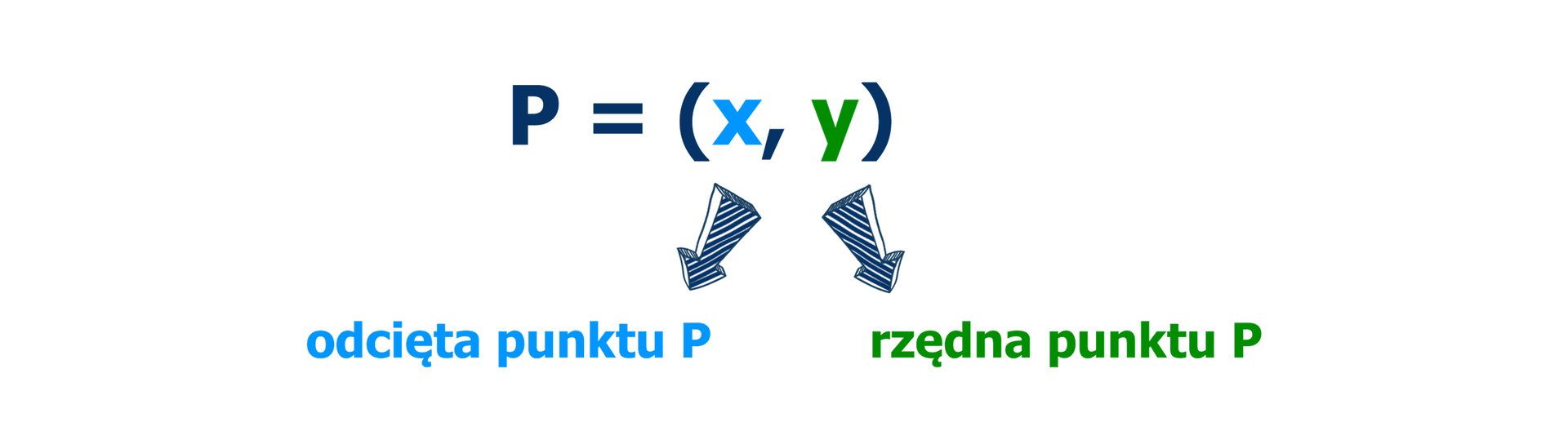
Pierwsza współrzędna określa położenie punktu względem osi , a druga – względem osi .
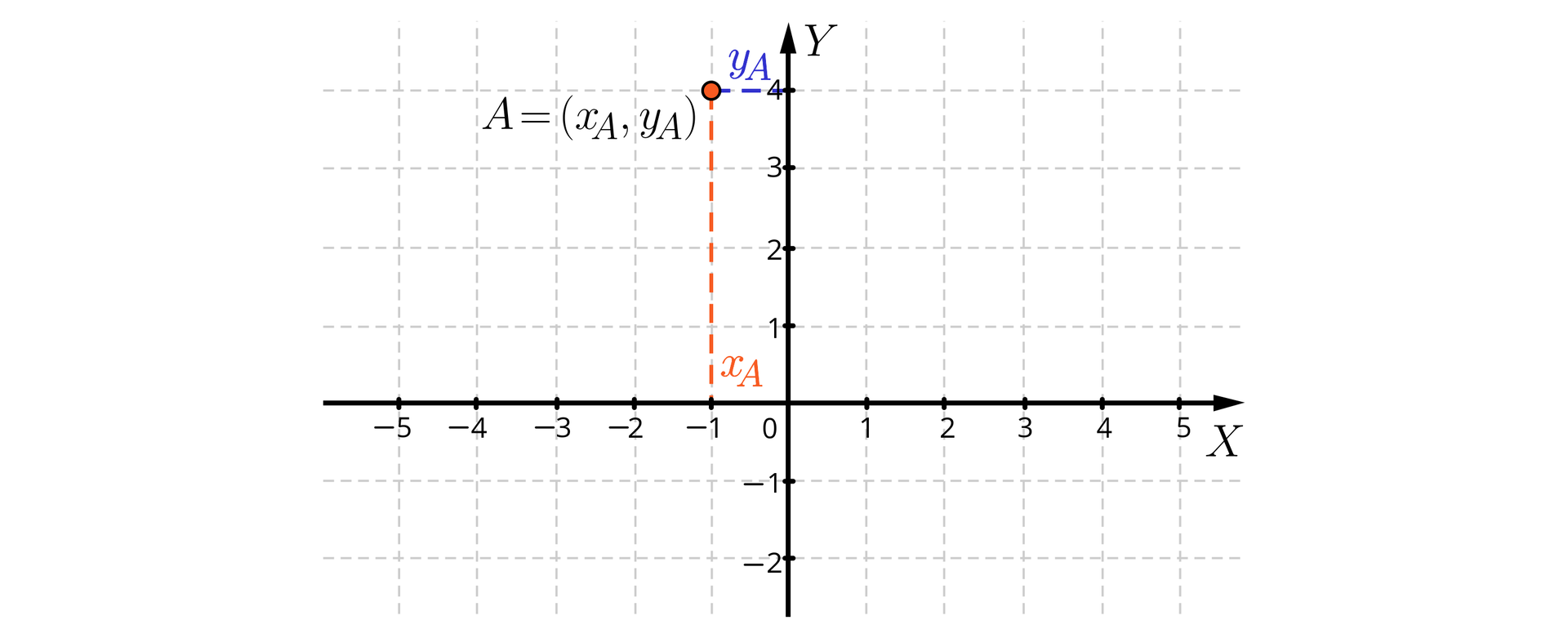
Aby wyznaczyć pierwszą współrzędną punktu , można zaznaczyć prostą prostopadłą do osi przechodzącą przez punkt . Liczba odpowiadająca punktowi, w którym ta prosta przecina oś , jest pierwszą współrzędną punktu – odciętą punktu .
Aby wyznaczyć drugą współrzędną punktu , można zaznaczyć prostą prostopadłą do osi , przechodzącą przez punkt . Liczba odpowiadająca punktowi, w którym ta prosta przecina oś , jest drugą współrzędną punktu – rzędną punktu .

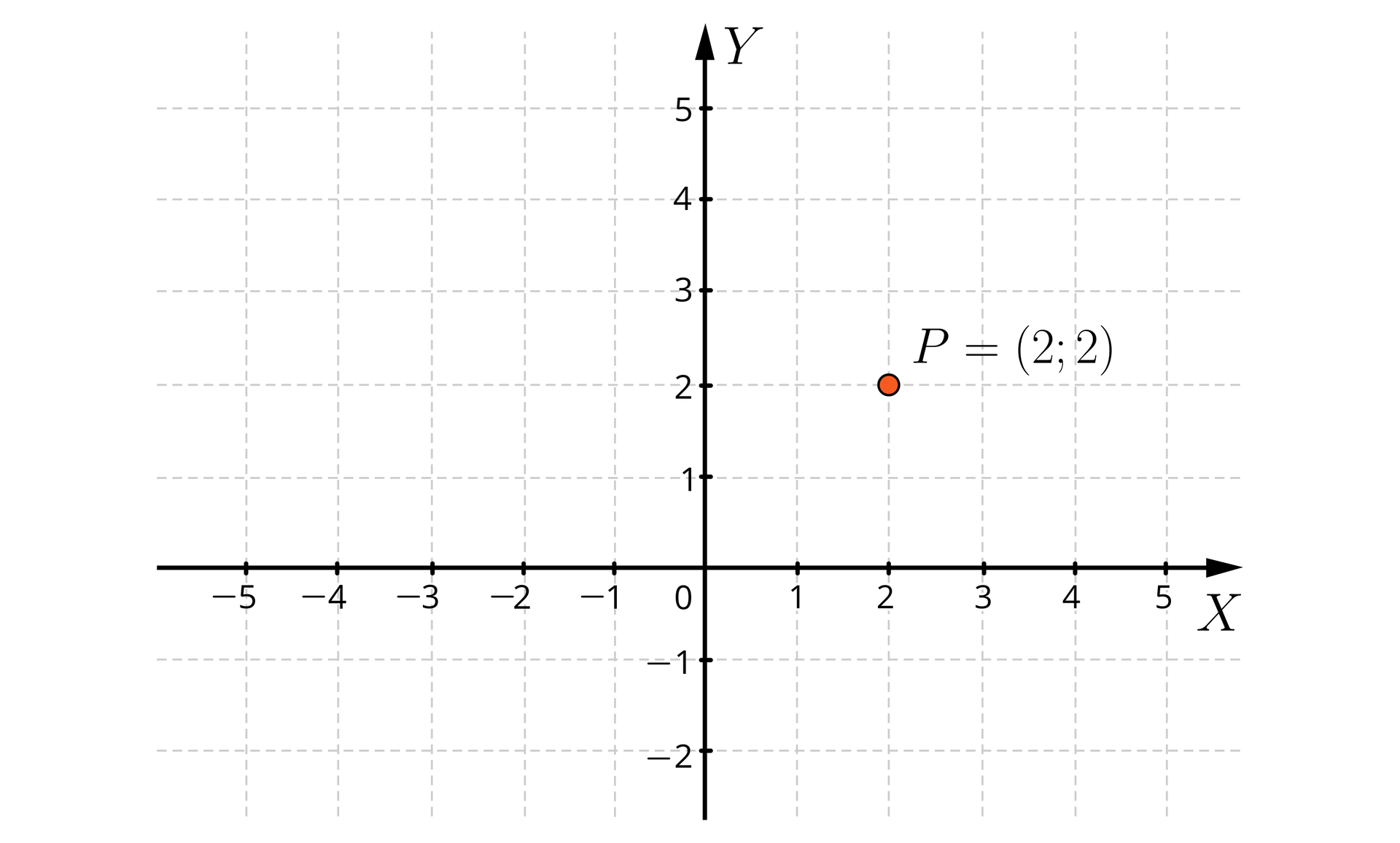
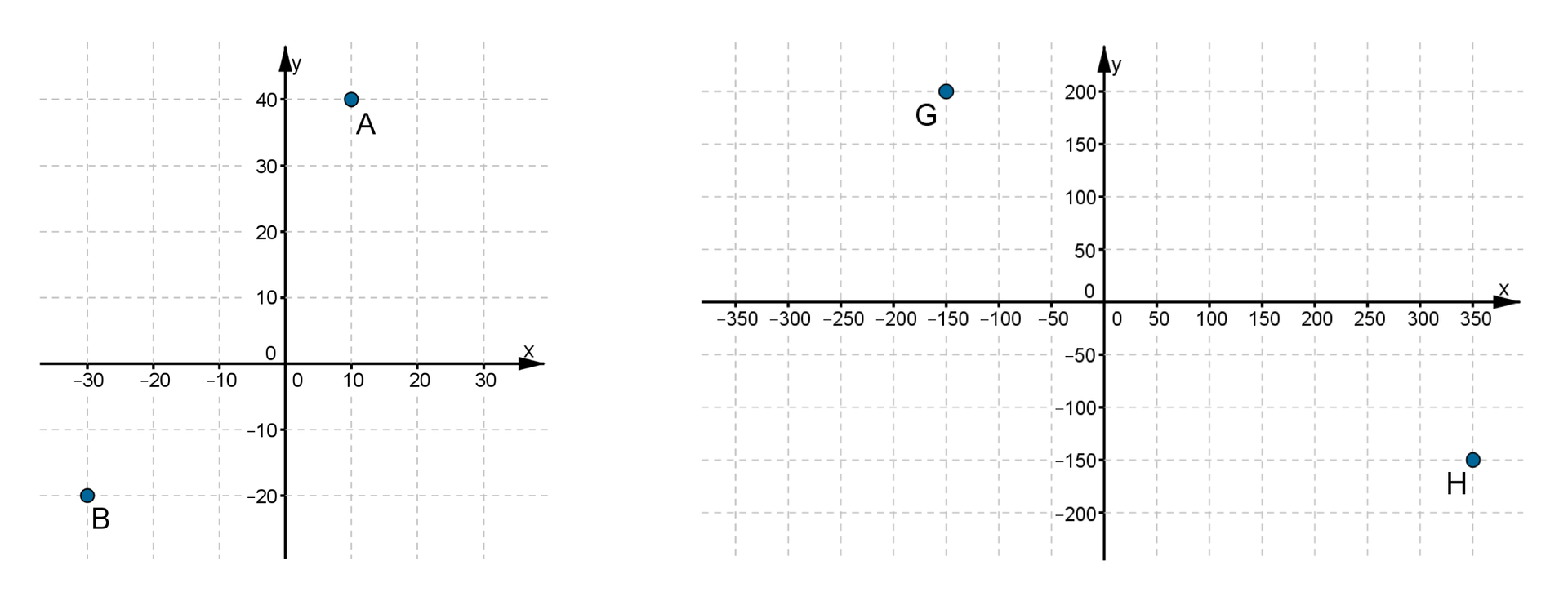
Współrzędne punktu : pierwsza współrzędna to , a druga to . Zapisujemy .
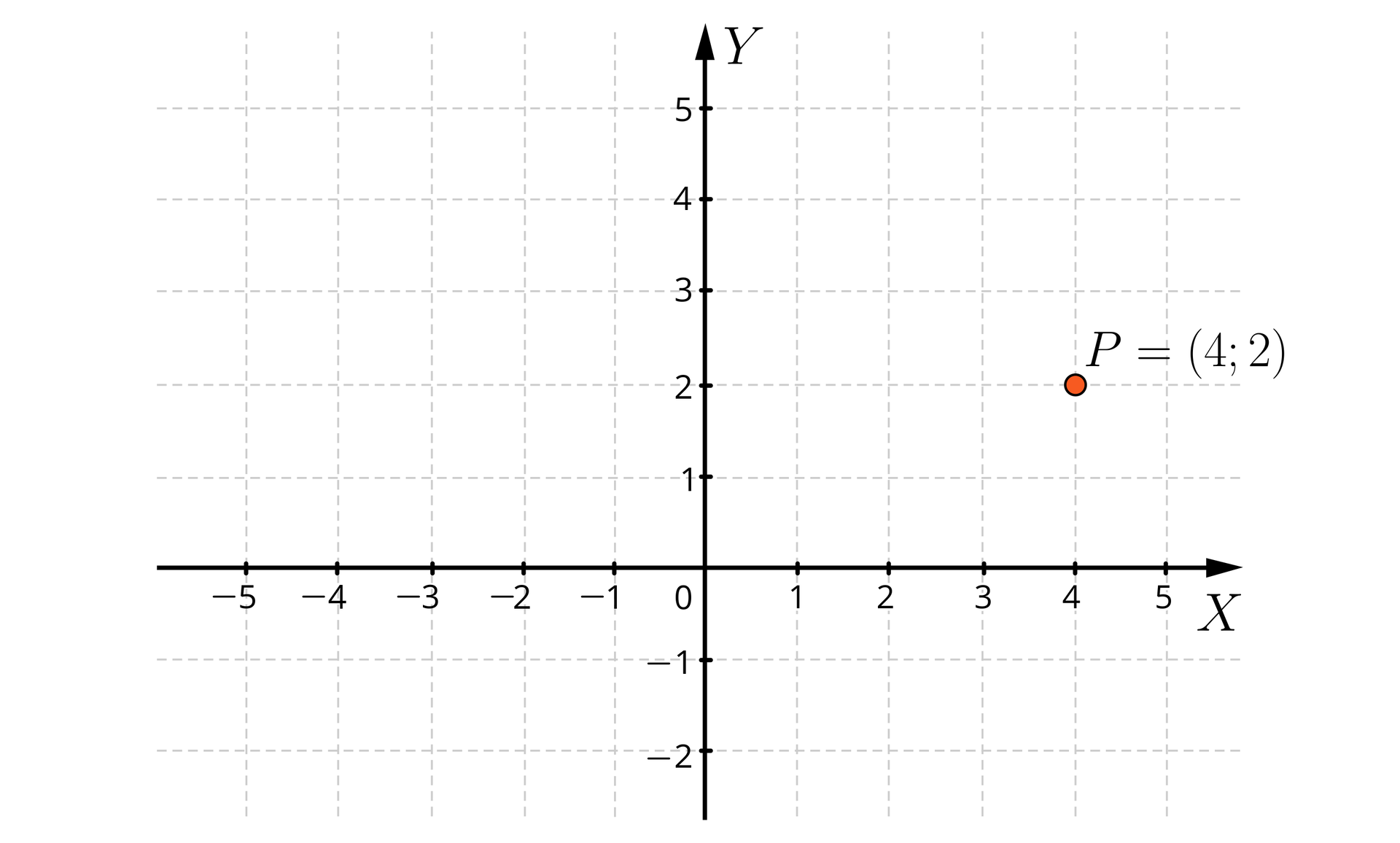
Współrzędne punktu : pierwsza współrzędna to , a druga to . Zapisujemy .
Współrzędne punktu : pierwsza współrzędna to , a druga to . Zapisujemy .
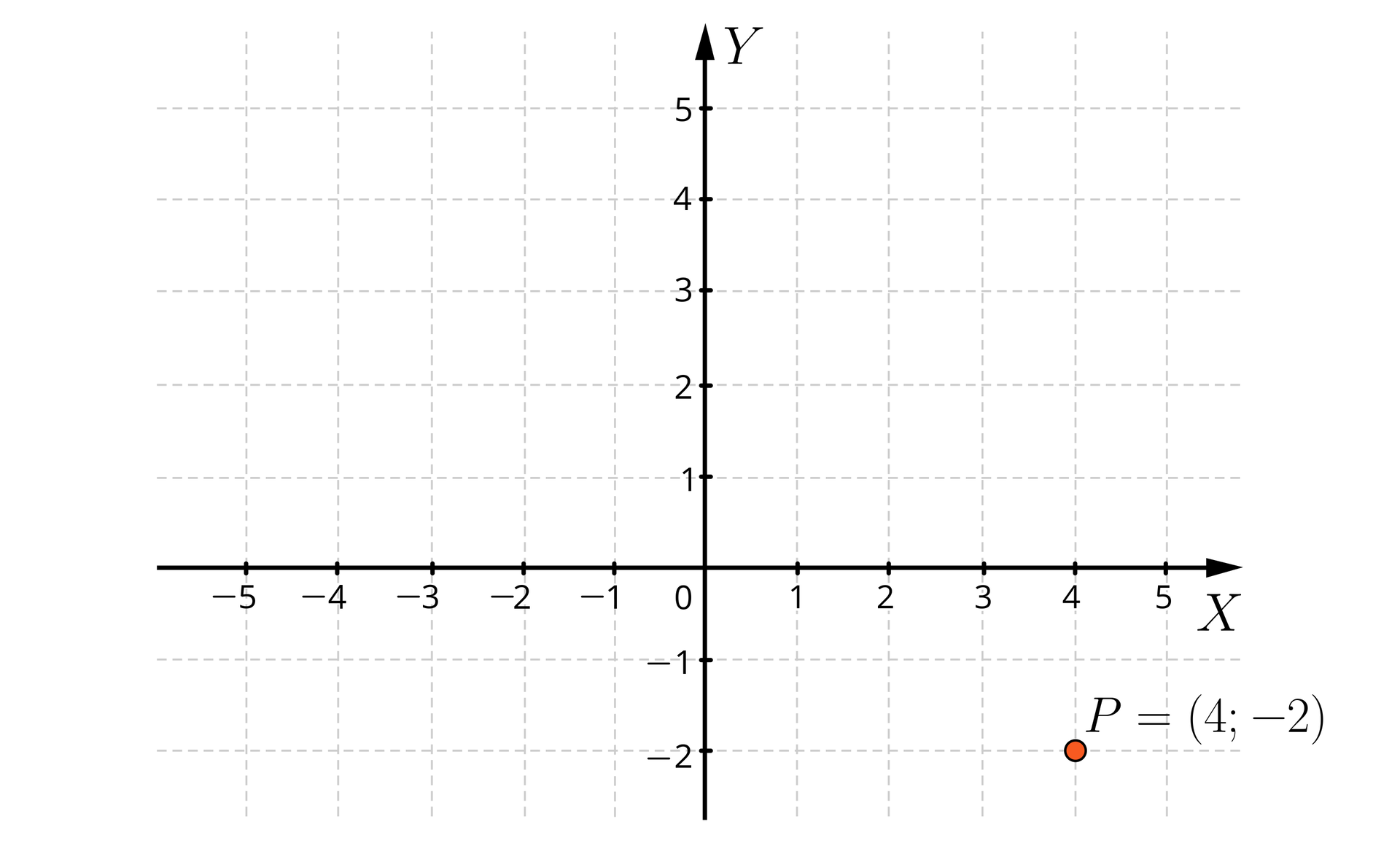
Współrzędne punktu : pierwsza współrzędna to , a druga to . Zapisujemy .
Najczęściej na obu osiach układu współrzędnych obieramy jednakowe jednostki tak, aby można było zaznaczyć dane punkty.
W zastosowaniach praktycznych, gdy na osiach układu współrzędnych zaznaczane są różne wielkości, jednostki mogą mieć różne długości.
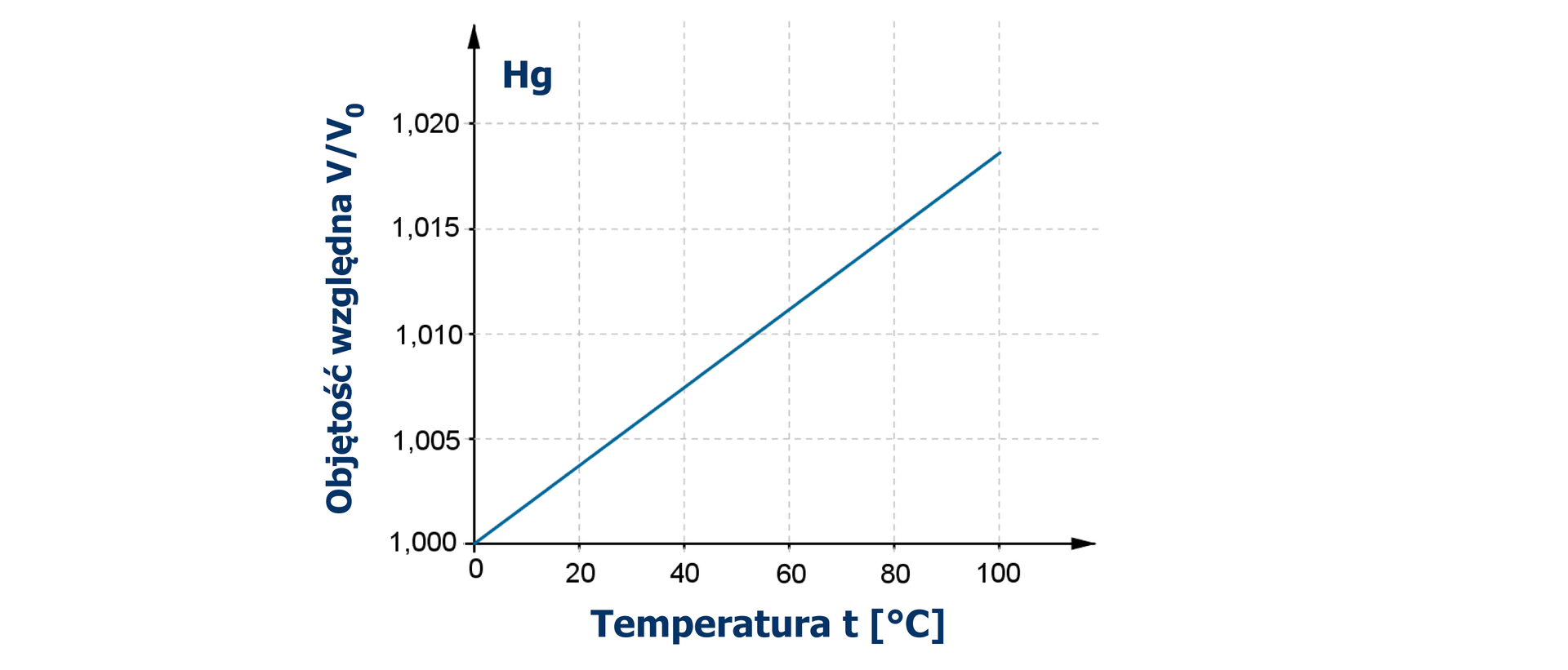
Wykres zmiany objętości rtęci w zależności od temperatury.
W układzie współrzędnych zaznaczone są punkty leżące na osiach układu.

Odczytajmy ich współrzędne.
Punkty leżące na osi :
, , , , , .
Punkty leżące na osi :
, , , , , .
Zauważmy, że
punkty leżące na osi mają drugą współrzędną równą ,
punkty leżące na osi mają pierwszą współrzędną równą .
Początek układu współrzędnych (punkt ) ma współrzędne .
Podaj współrzędne punktu .
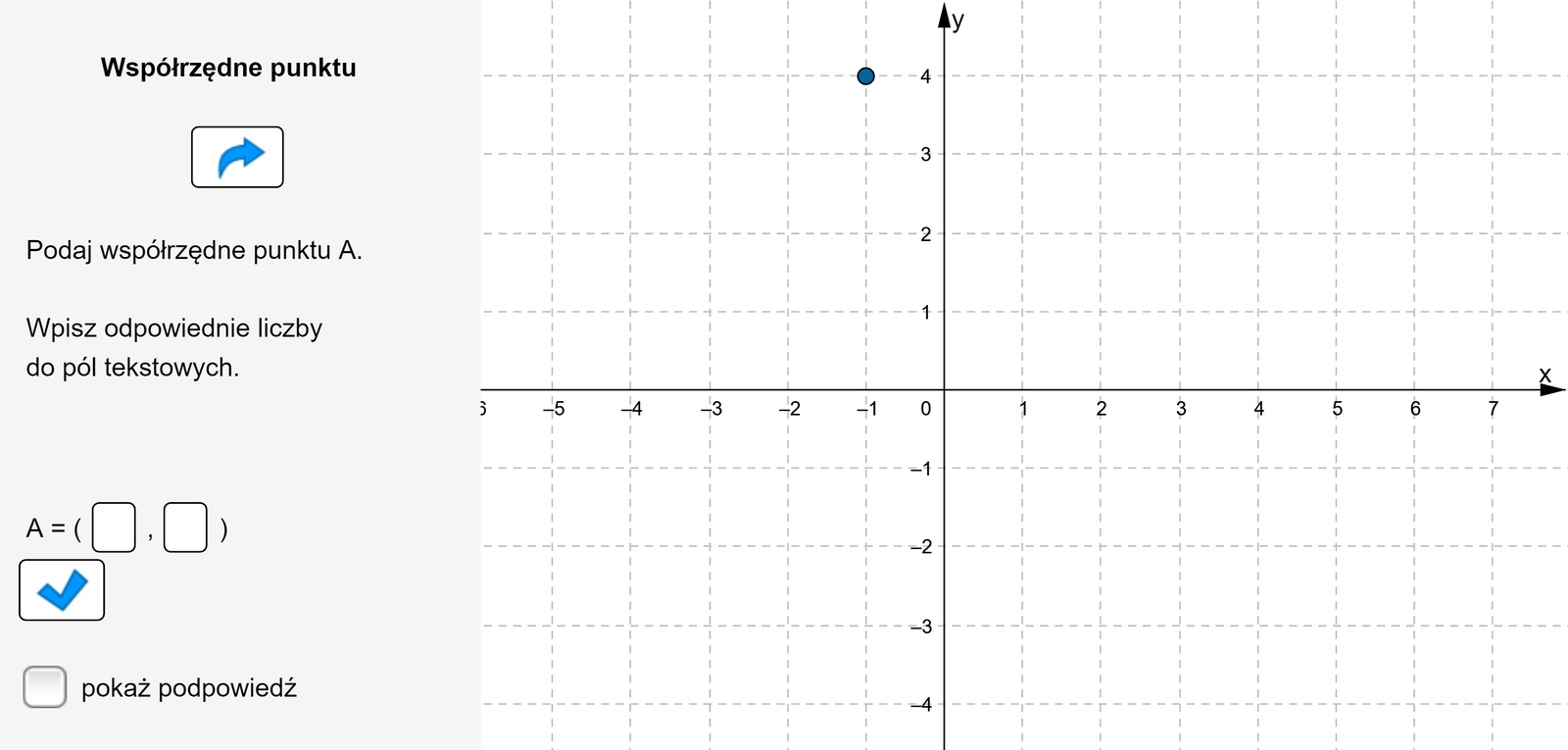
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/D91NVnRlI
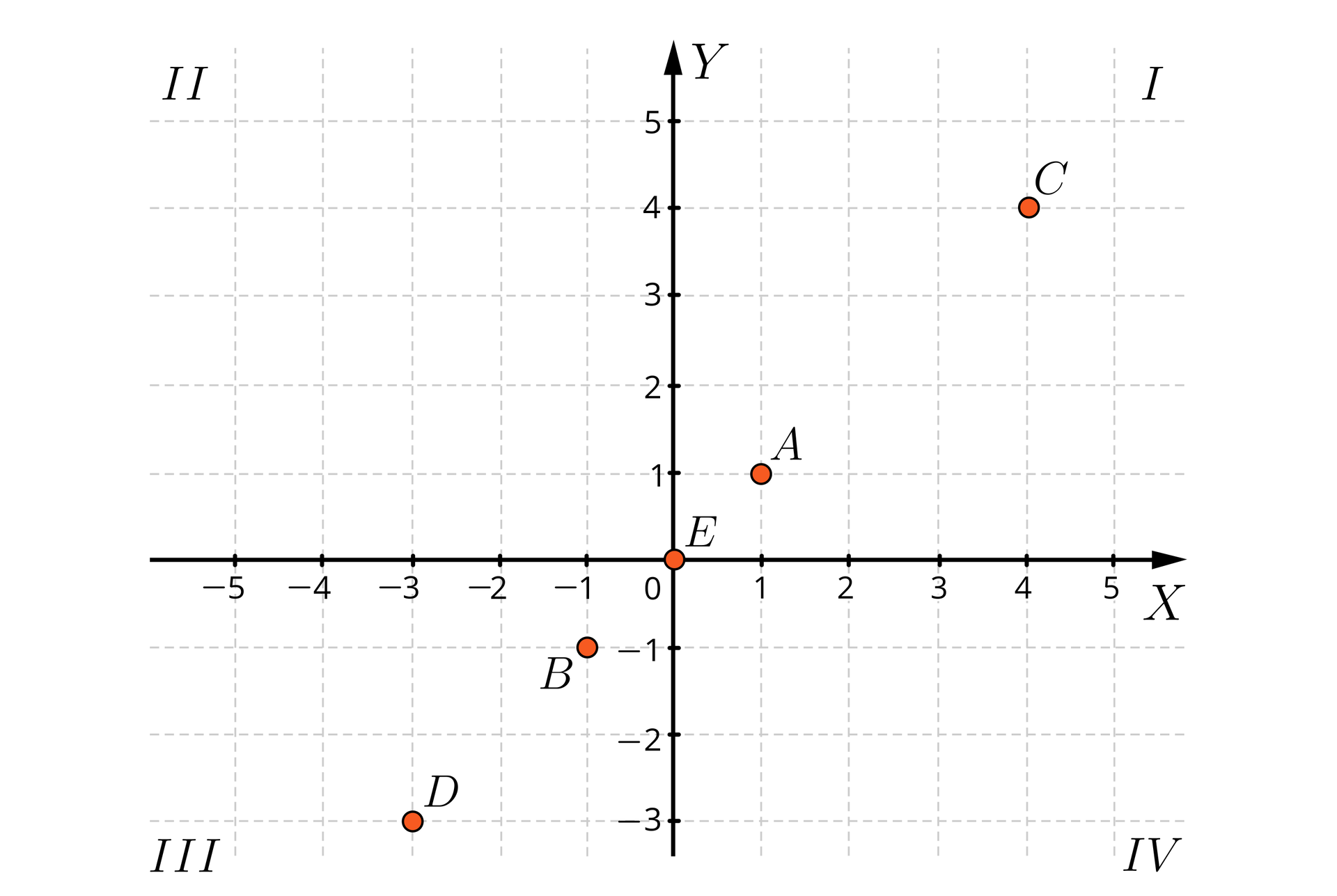
Odczytaj współrzędne zaznaczonych punktów.

W poniższym układzie współrzędnych zostało zaznaczonych sześć punktów: , , , , , . Wyznacz ich współrzędne.

W układzie współrzędnych ustaw punkt tak, aby miał dane współrzędne.
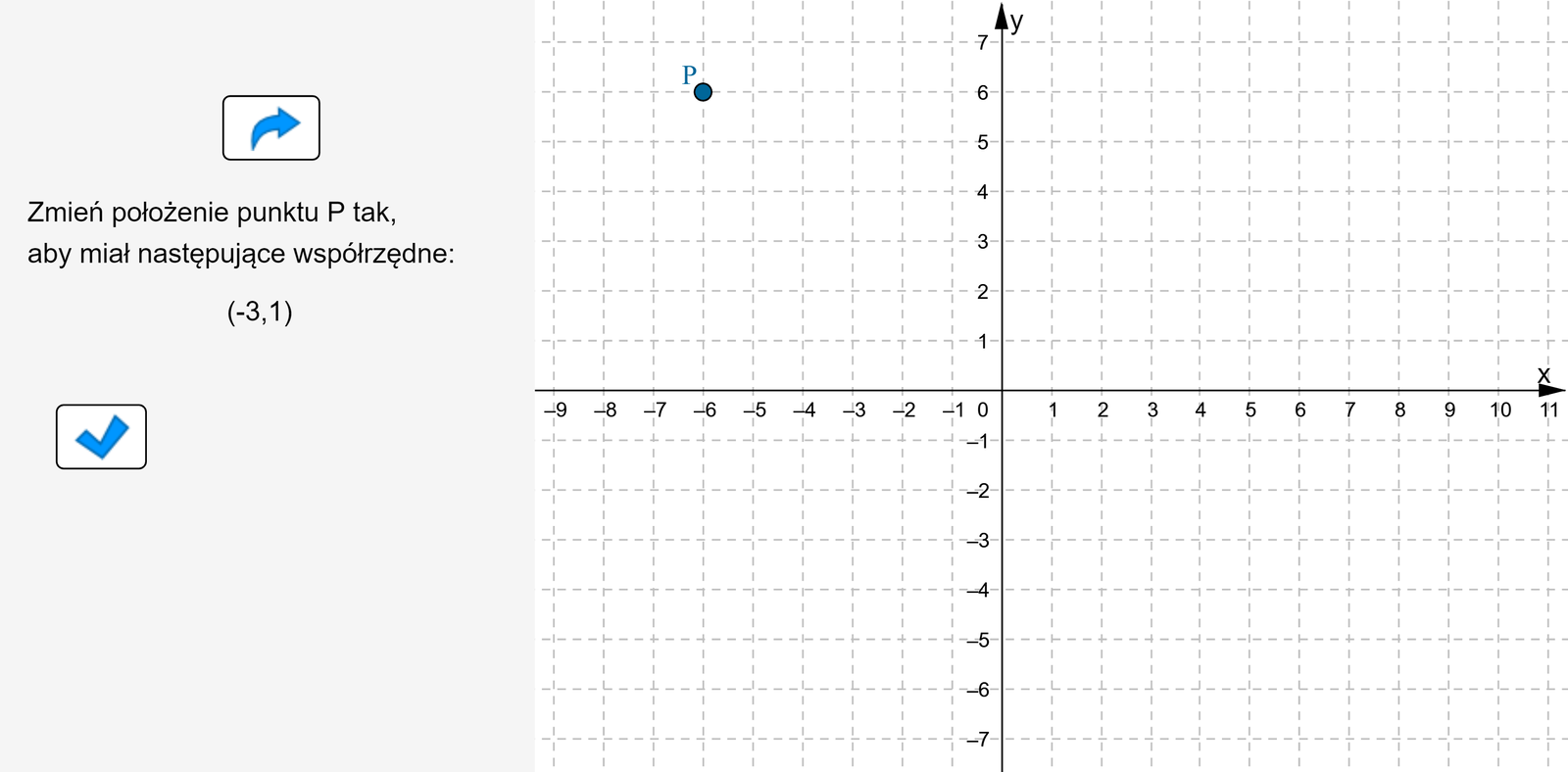
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/D91NVnRlI
Ćwiartki układu współrzędnych
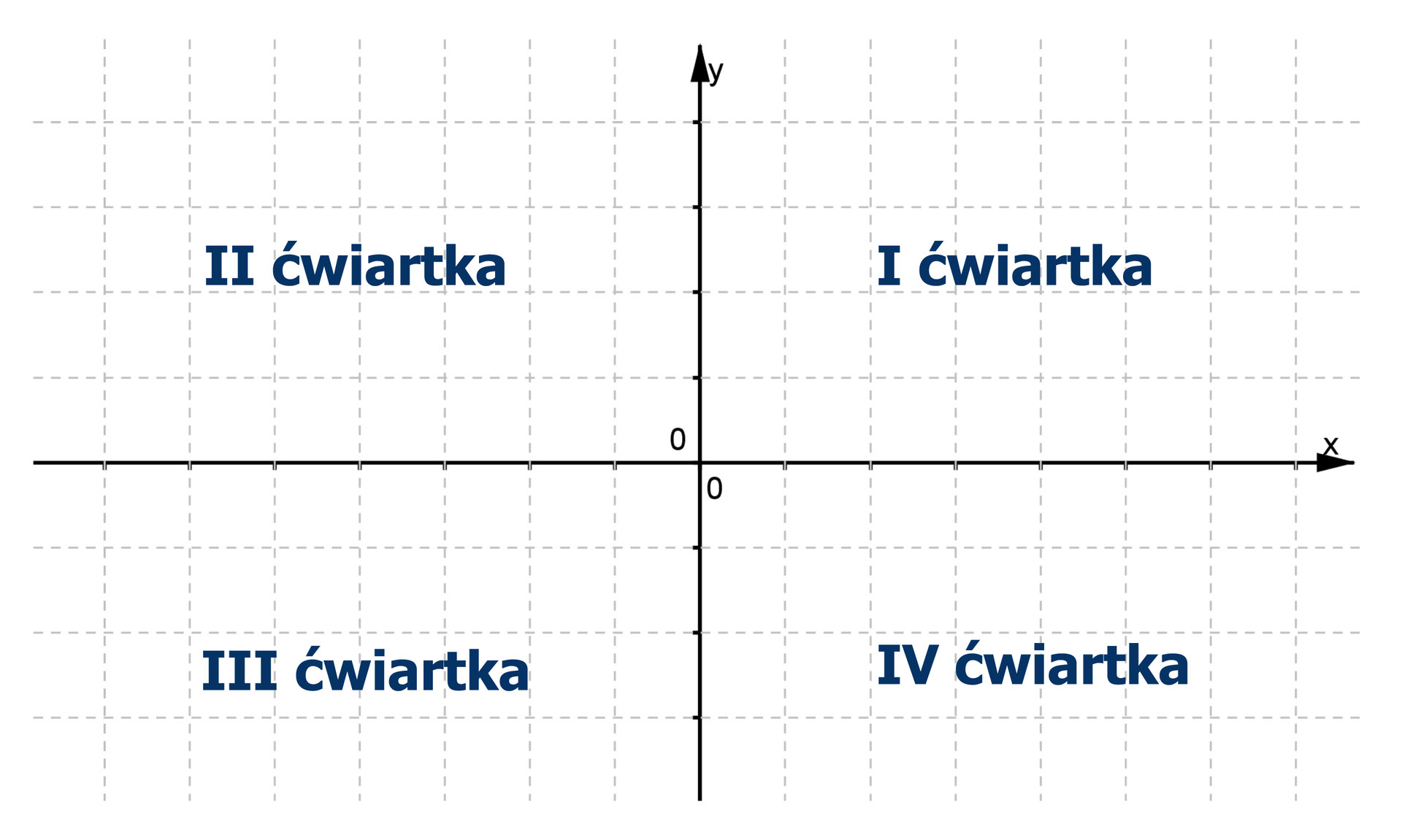
Osie układu współrzędnych dzielą płaszczyznę na cztery części nazywane ćwiartkami.
Ćwiartki numerujemy cyframi rzymskimi: , , , przeciwnie do ruchu wskazówek zegara.
Punktów leżących na osiach układu współrzędnych nie zaliczamy do żadnej ćwiartki.
Zmieniaj położenie punktu zaznaczonego w układzie współrzędnych.
Zaobserwuj znaki pierwszej oraz drugiej współrzędnej punktu w poszczególnych ćwiartkach układu współrzędnych.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/D91NVnRlI
Zwróć uwagę na fakt, iż w zależności od tego, w jakiej ćwiartce znajduje się punkt, takie ma współrzędne. Każda ćwiartka wyznaczona jest z innej kombinacji półosi dodatnich i ujemnych, zatem mamy cztery klasy współrzędnych.
Jeżeli punkt należy do:
ćwiartki układu współrzędnych, to obie jego współrzędne są liczbami dodatnimi,
ćwiartki układu współrzędnych, to jego pierwsza współrzędna jest liczbą ujemną, a druga dodatnią,
ćwiartki układu współrzędnych, to obie jego współrzędne są liczbami ujemnymi,
ćwiartki układu współrzędnych, to jego pierwsza współrzędna jest liczbą dodatnią, a druga ujemną.

Podaj współrzędne punktów , oraz i sprawdzaj ich poprawność za pomocą testera.
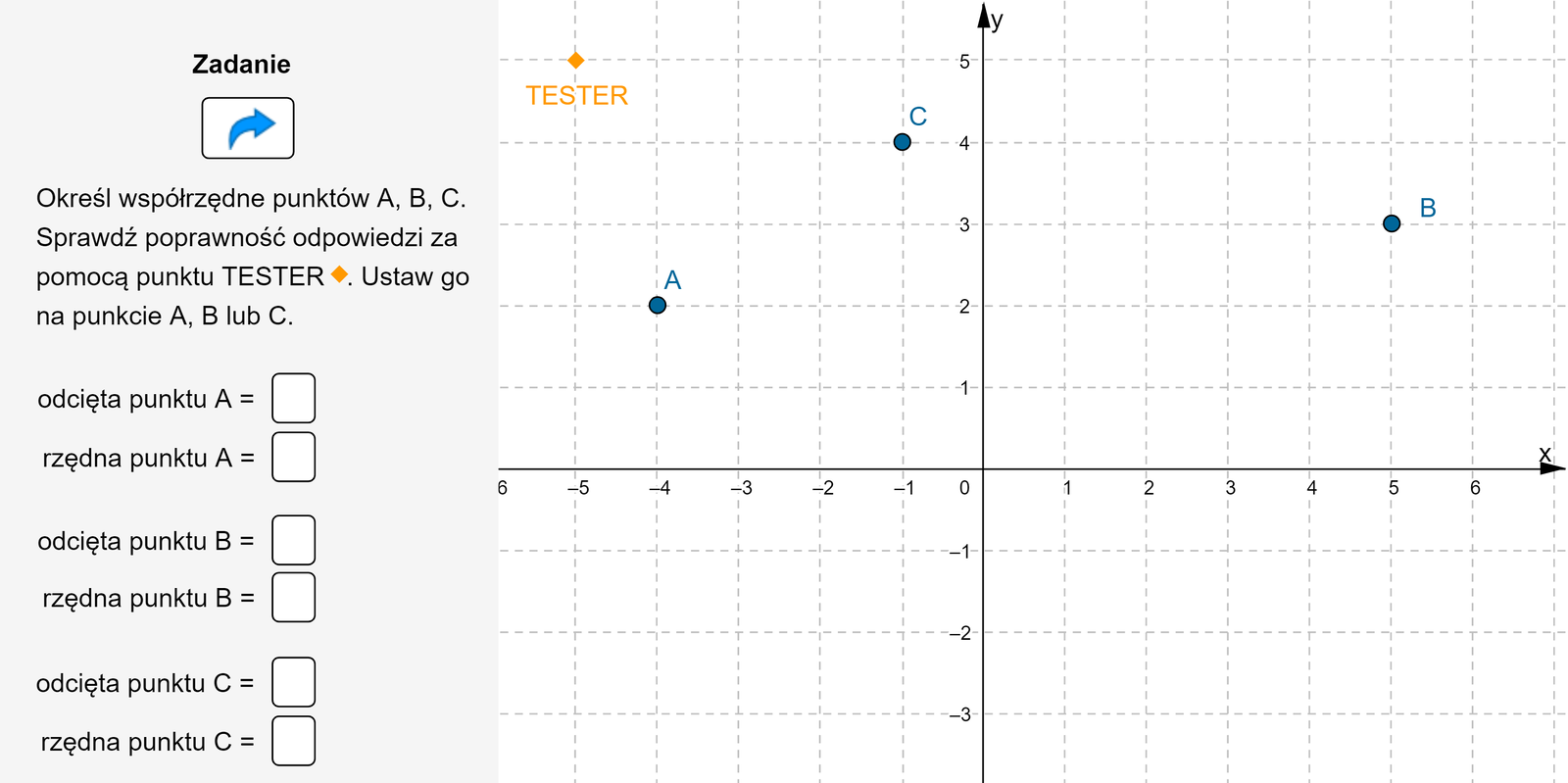
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/D91NVnRlI
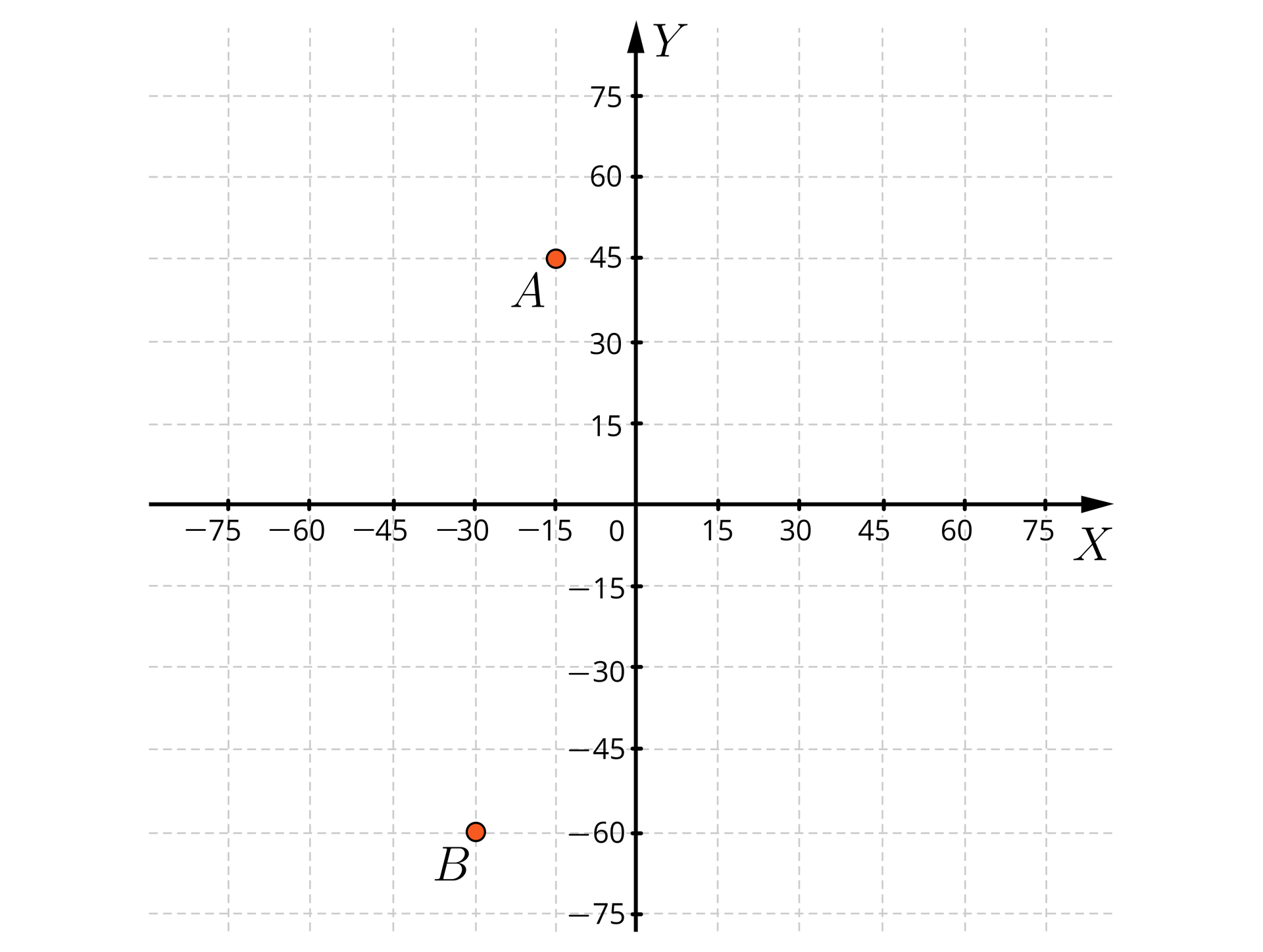
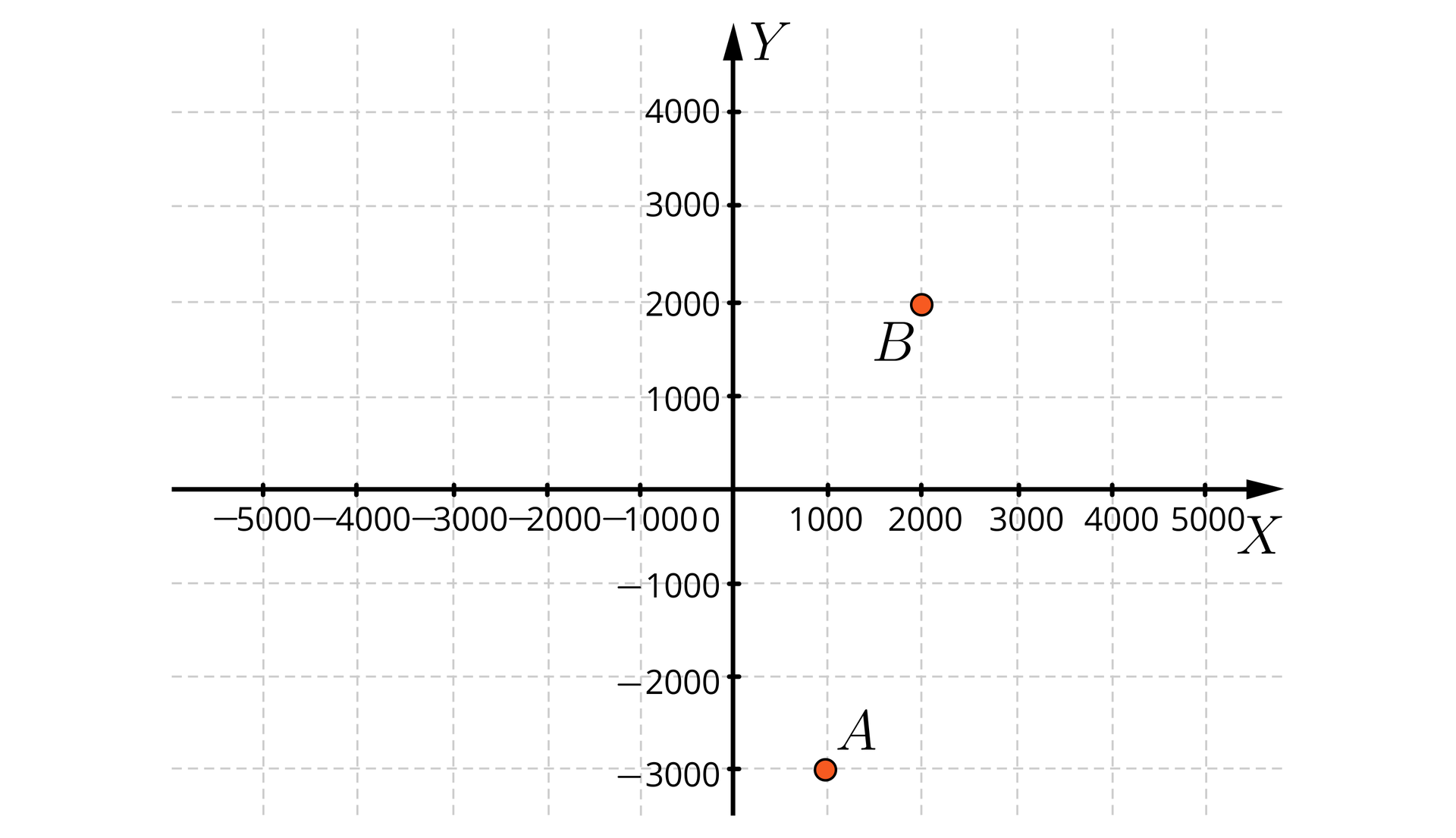
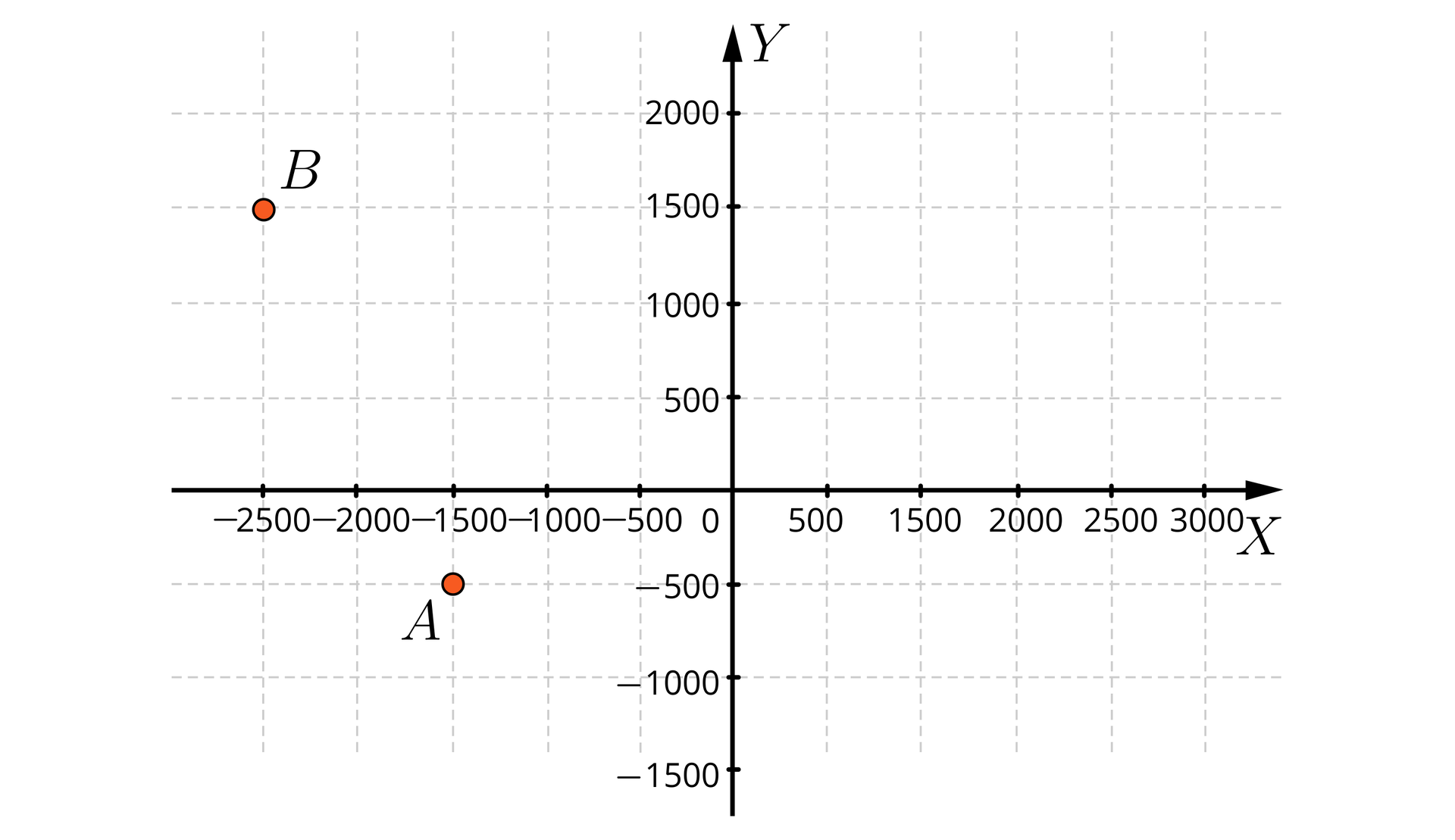
Narysuj układ współrzędnych; dobierz odpowiednio jednostkę i zaznacz punkty i .
,
,
,
,
,
,
Punkt znajduje się w układzie współrzędnych na osi odciętych, gdy: Możliwe odpowiedzi: 1. , 2. , 3. , 4. , 5. , 6.
Zaznacz prawidłową odpowiedź. Możliwe odpowiedzi: 1. , 2. , 3. , 4.
- Tak, ponieważ odcięta jest liczbą ujemną
- Nie, ponieważ odcięta jest liczbą ujemną
- Tak, ponieważ rzędna jest liczbą ujemną.
- Nie, ponieważ obie współrzędne są ujemne.
- Tak, ponieważ obie współrzędne są ujemne.
Przeciągnij punkty do odpowiedniej ćwiartki układu współrzędnych.
<span aria-label="H, równa się, nawias trzysta dwanaście przecinek jeden trzy dwa zamknięcie nawiasu" role="math"><math><mi>H</mi><mo>=</mo><mo>(</mo><mn>312</mn><mo>,</mo><mn>132</mn><mo>)</mo></math></span>, <span aria-label="C, równa się, nawias, minus, dwadzieścia trzy, przecinek, minus, trzydzieści trzy zamknięcie nawiasu" role="math"><math><mi>C</mi><mo>=</mo><mo>(</mo><mo>-</mo><mn>23</mn><mo>,</mo><mo>-</mo><mn>33</mn><mo>)</mo></math></span>, <span aria-label="F, równa się, nawias, minus, osiemset dziewięć przecinek dziewięć zamknięcie nawiasu" role="math"><math><mi>F</mi><mo>=</mo><mo>(</mo><mo>-</mo><mn>809</mn><mo>,</mo><mn>9</mn><mo>)</mo></math></span>, <span aria-label="I, równa się, nawias dziesięć, przecinek, minus, jeden zamknięcie nawiasu" role="math"><math><mi>I</mi><mo>=</mo><mo>(</mo><mn>10</mn><mo>,</mo><mo>-</mo><mn>1</mn><mo>)</mo></math></span>, <span aria-label="B, równa się, nawias, minus, dwadzieścia sześć przecinek jeden osiem siedem zamknięcie nawiasu" role="math"><math><mi>B</mi><mo>=</mo><mo>(</mo><mo>-</mo><mn>26</mn><mo>,</mo><mn>187</mn><mo>)</mo></math></span>, <span aria-label="A, równa się, nawias dwanaście przecinek trzy dwa zamknięcie nawiasu" role="math"><math><mi>A</mi><mo>=</mo><mo>(</mo><mn>12</mn><mo>,</mo><mn>32</mn><mo>)</mo></math></span>, <span aria-label="E, równa się, nawias sto, przecinek, minus, siedemset sześćdziesiąt pięć zamknięcie nawiasu" role="math"><math><mi>E</mi><mo>=</mo><mo>(</mo><mn>100</mn><mo>,</mo><mo>-</mo><mn>765</mn><mo>)</mo></math></span>, <span aria-label="G, równa się, nawias, minus, dziewięćdziesiąt jeden, przecinek, minus, trzy zamknięcie nawiasu" role="math"><math><mi>G</mi><mo>=</mo><mo>(</mo><mo>-</mo><mn>91</mn><mo>,</mo><mo>-</mo><mn>3</mn><mo>)</mo></math></span>, <span aria-label="D, równa się, nawias, minus, trzysta sześćdziesiąt pięć przecinek dwa zamknięcie nawiasu" role="math"><math><mi>D</mi><mo>=</mo><mo>(</mo><mo>-</mo><mn>365</mn><mo>,</mo><mn>2</mn><mo>)</mo></math></span>
| I ćwiartka | |
|---|---|
| II ćwiartka | |
| III ćwiartka | |
| IV ćwiartka |
Jeżeli punkt znajduje się na osi , to Możliwe odpowiedzi: 1. , 2. , 3. , 4.
Jeżeli punkt znajduje się w ćwiartce układu współrzędnych, to liczba może być równa: Możliwe odpowiedzi: 1. , 2. , 3. , 4.
- Punkty i mają taką samą rzędną.
- Punkty i znajdują się na osi odciętych.
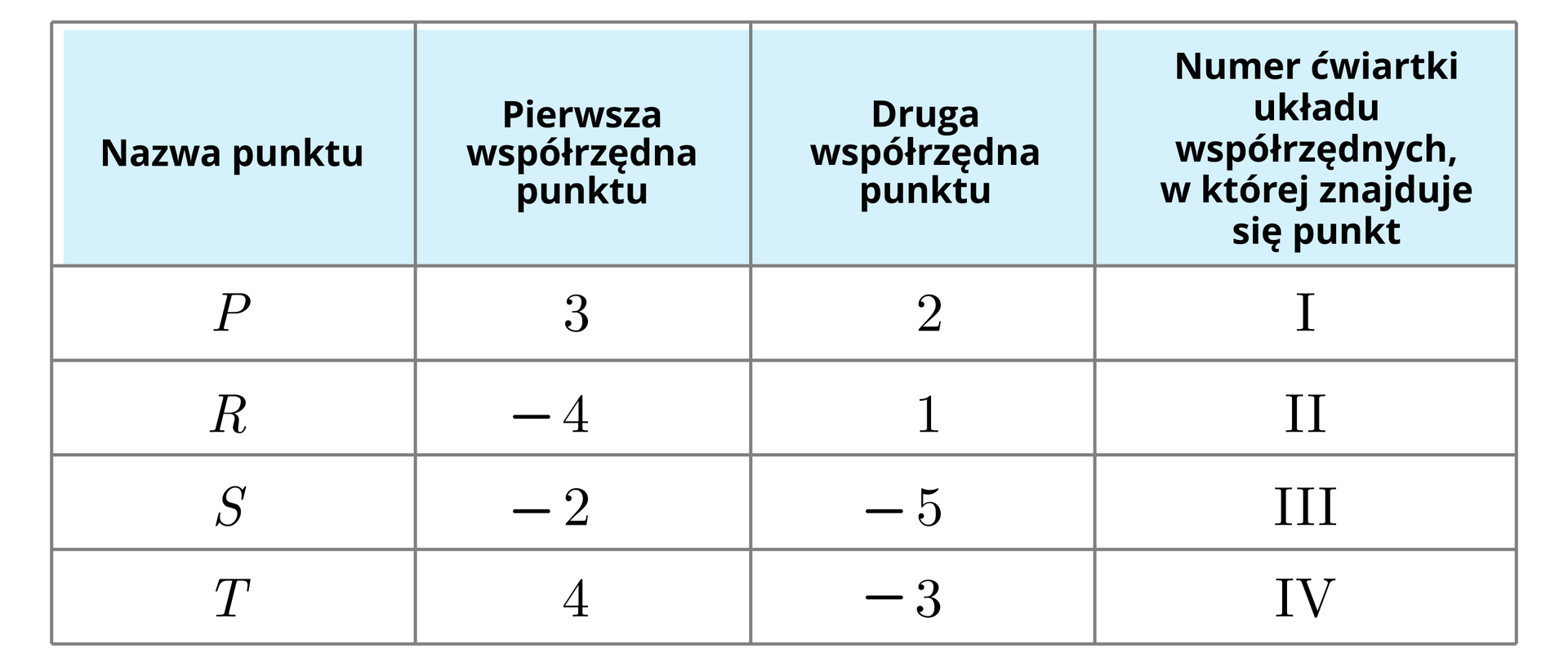
Zaznacz w układzie współrzędnych cztery różne punkty , , , , z których każdy znajduje się w innej ćwiartce układu współrzędnych. Odczytaj współrzędne tych punktów, przerysuj poniższą tabelę do zeszytu i uzupełnij odpowiednimi liczbami.
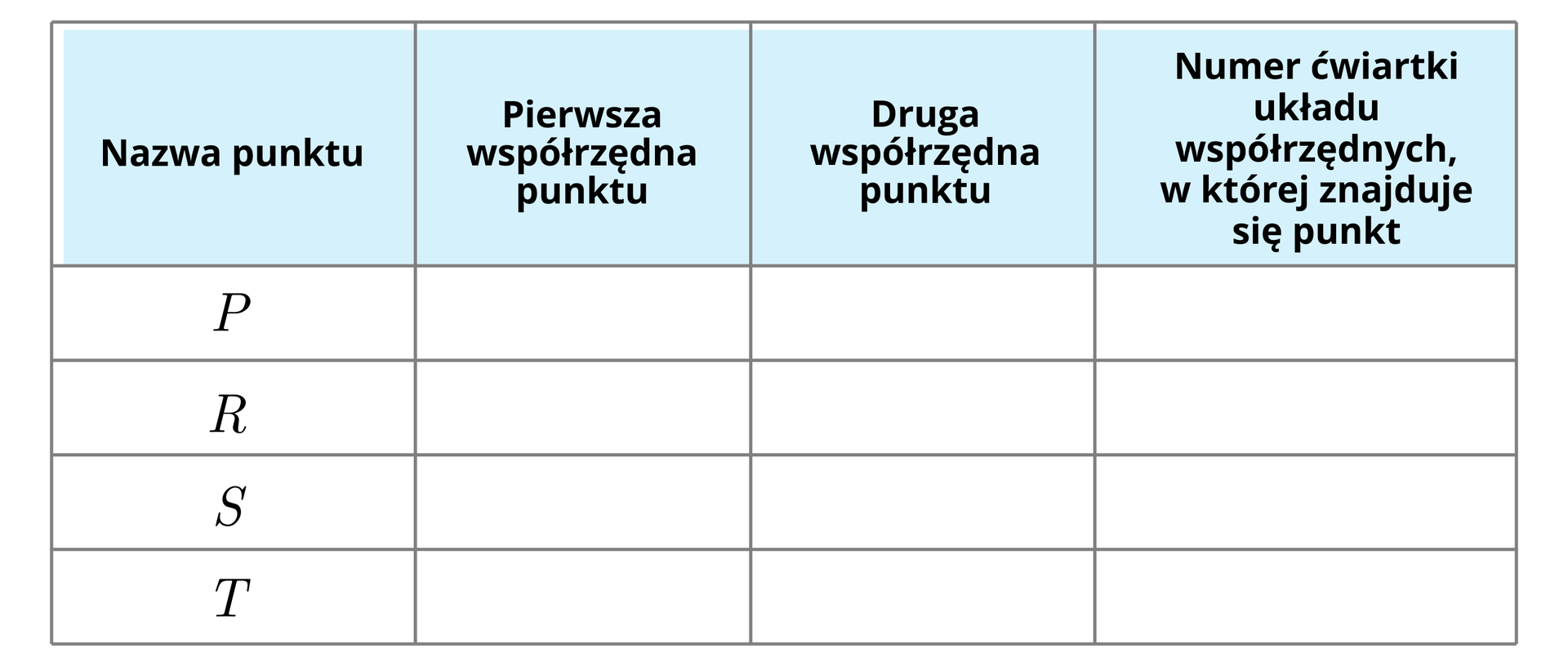
Zaznacz w układzie współrzędnych taki punkt , którego
Podaj współrzędne punktu , którego
obie współrzędne są równe,
druga współrzędna jest o mniejsza od pierwszej,
pierwsza współrzędna jest dwukrotnie większa od drugiej.
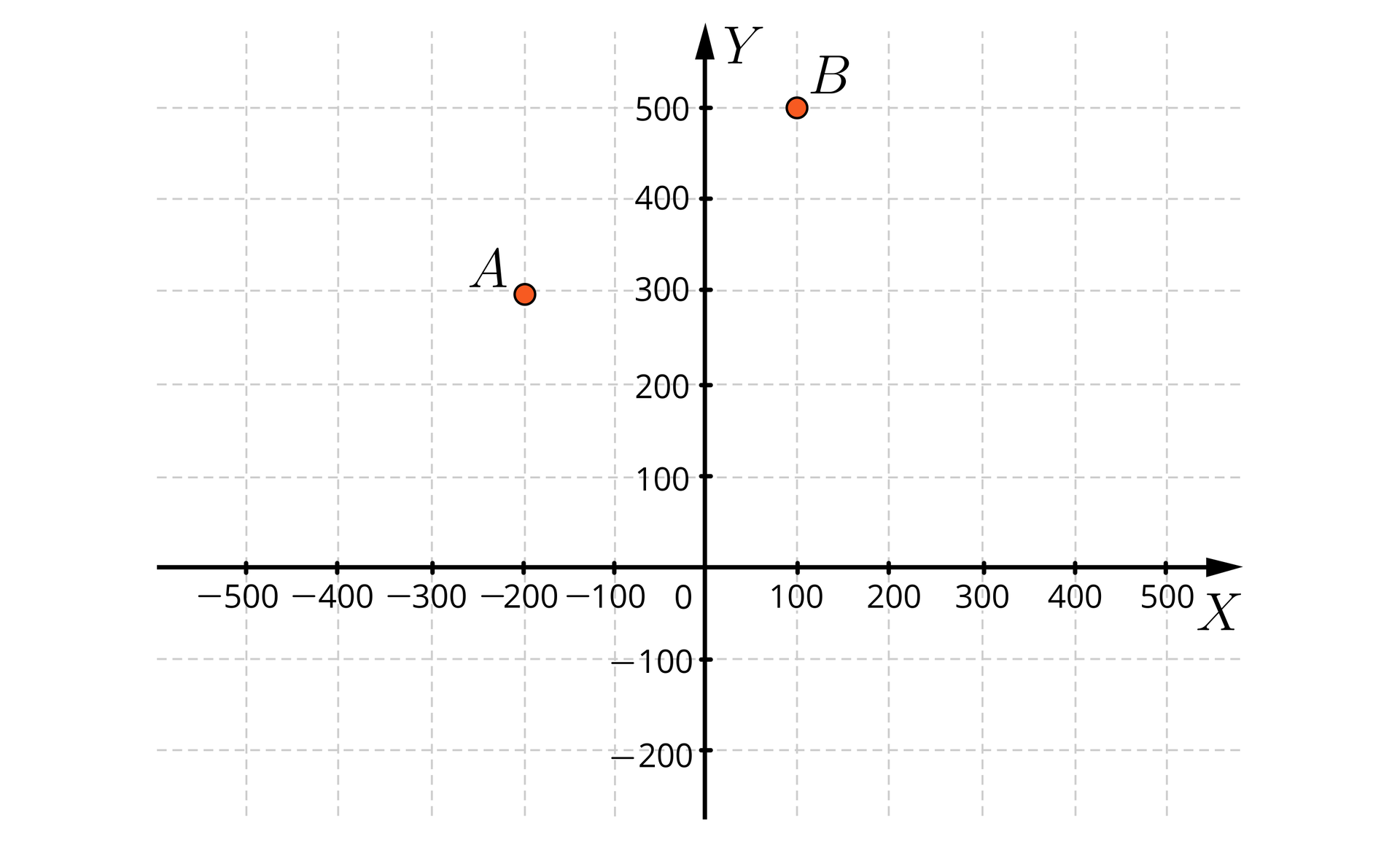
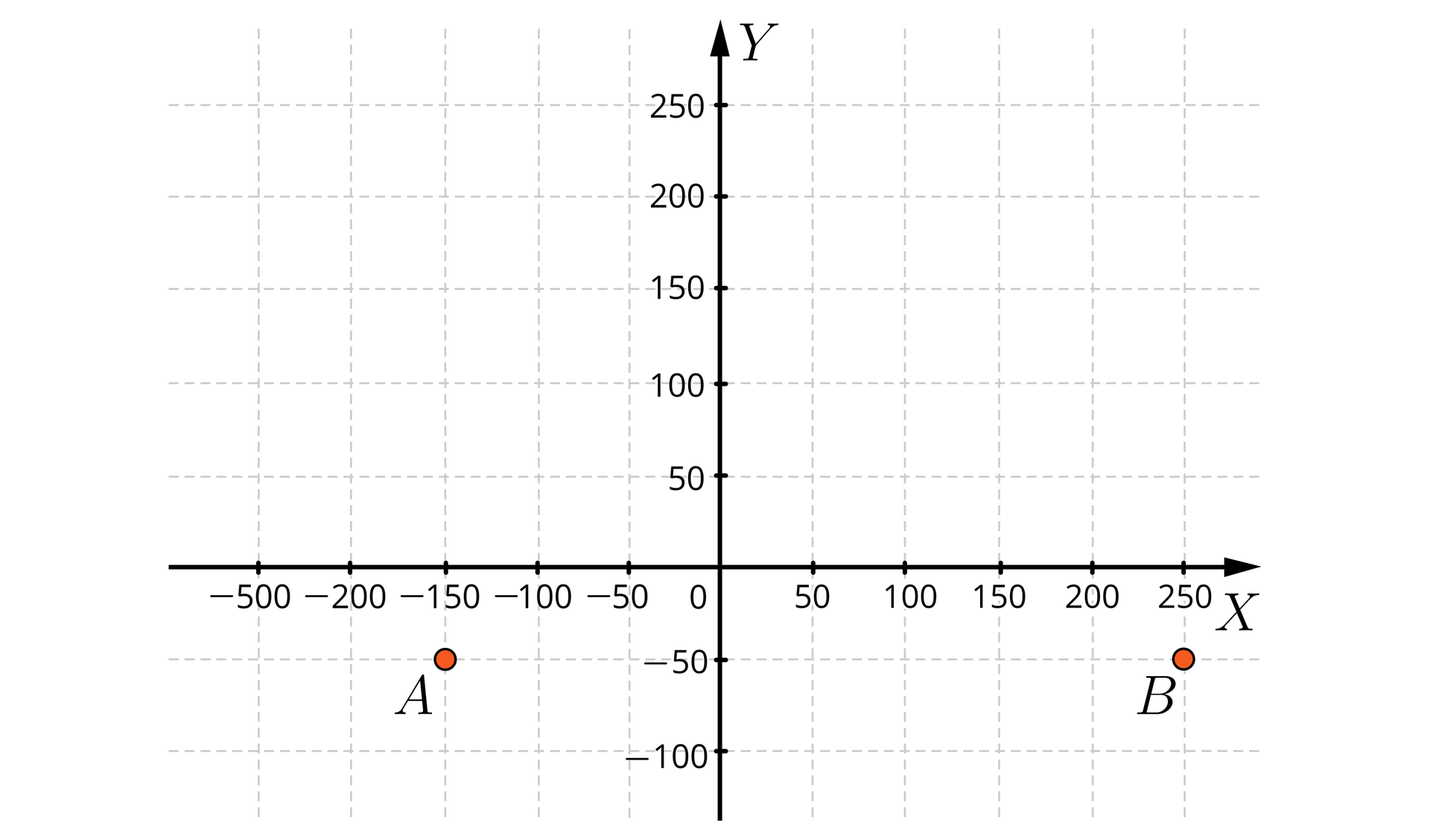
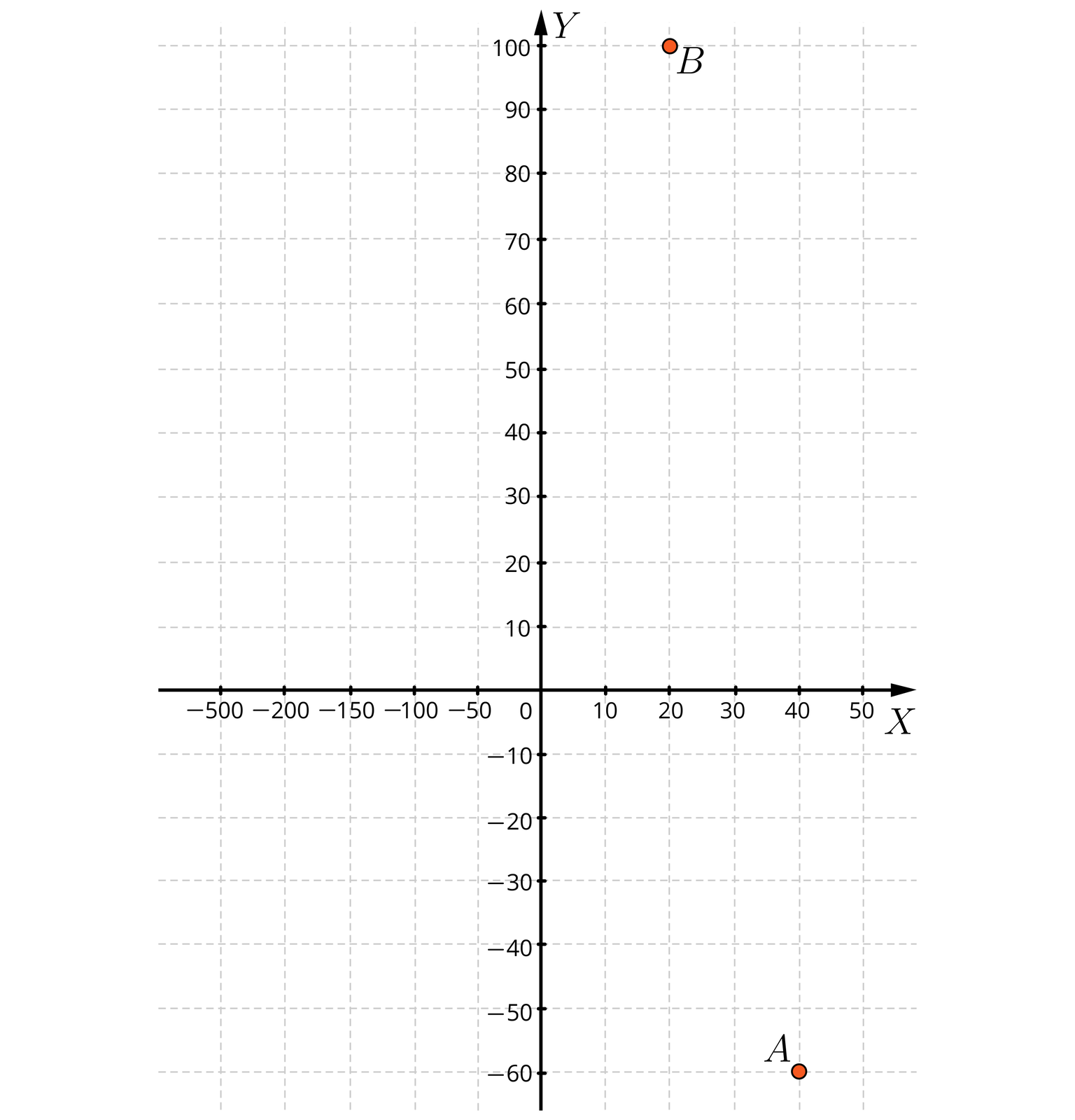
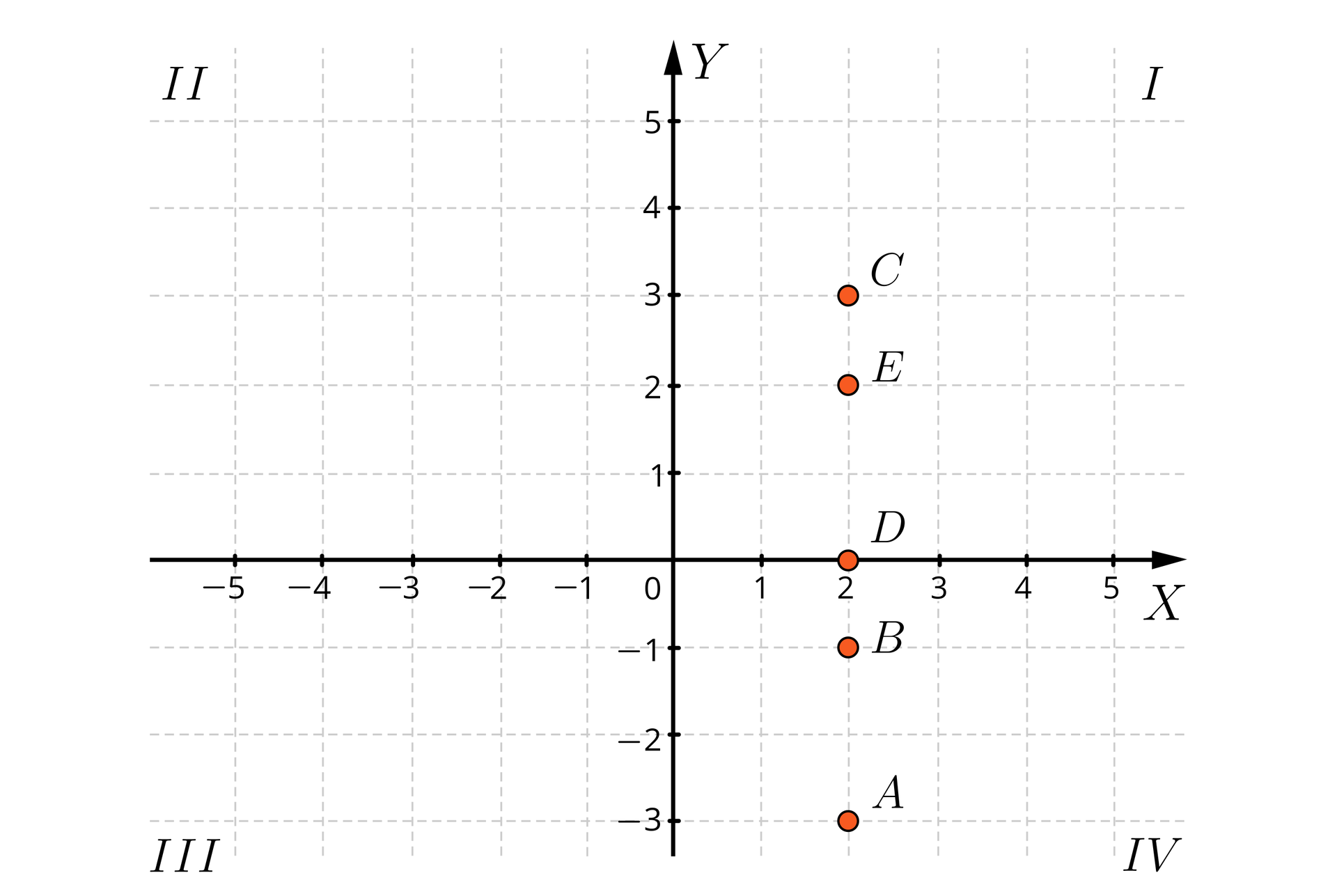
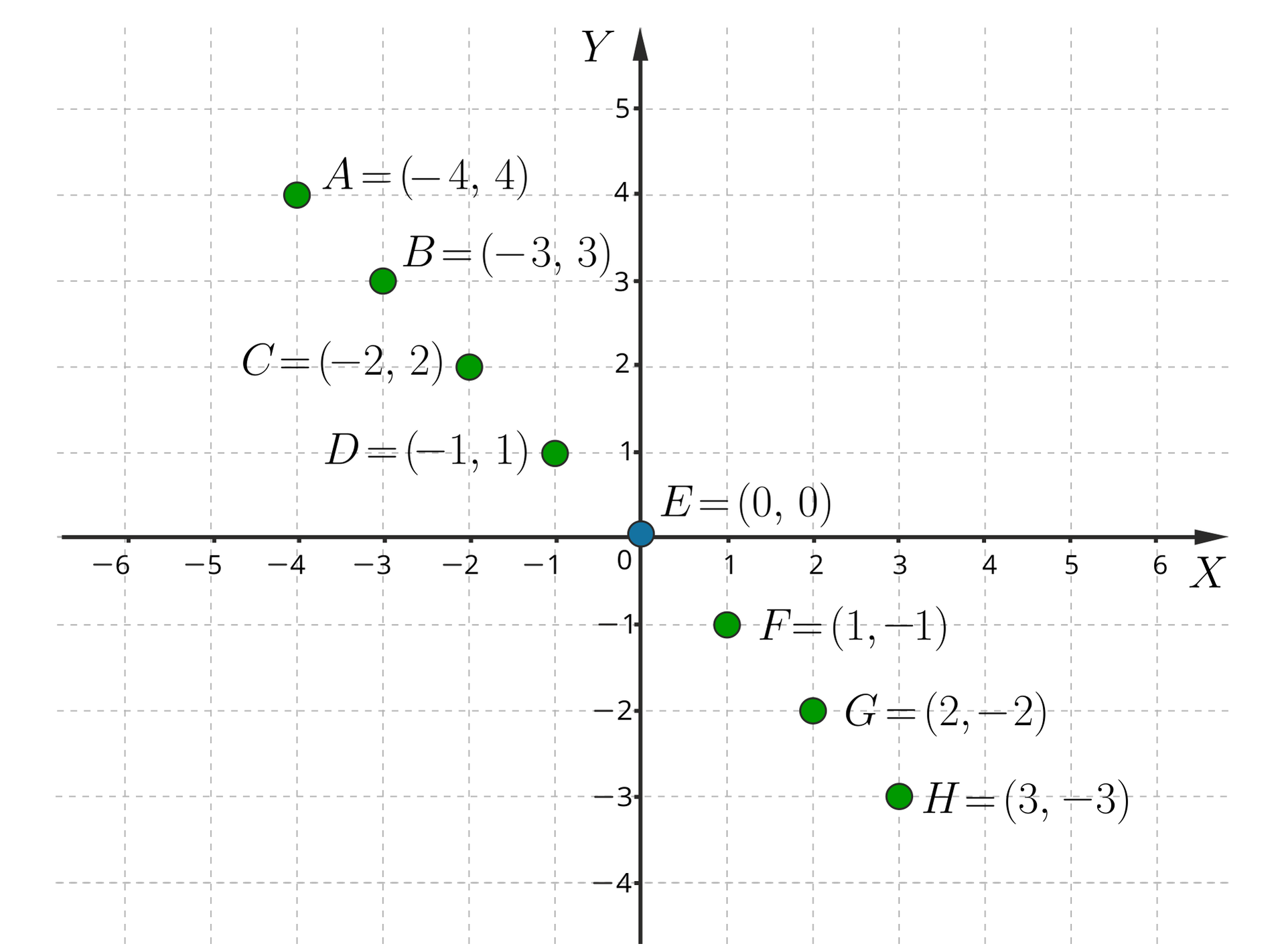
Zaznacz w układzie współrzędnych punkty , , , , . Co powiesz o ich wzajemnym położeniu?
Dane są punkty , , , , . Co powiesz o ich wzajemnym położeniu?
, , , ,
, , , ,
, , , ,
Odszyfruj sentencję, którą przypisuje się francuskiemu filozofowi Kartezjuszowi.
, , , , , , , , , , , ,
.

Punkty o współrzędnych wymiernych
W dalszej części materiału zawarte są informacje na temat punktów o współrzędnych wymiernych. Analizując zawarte tu przykłady, poznasz interpretację geometryczną takich punktów.
Z określeniem punktu w układzie współrzędnych spotykamy się wybierając miejsce na widowni kinowej czy teatralnej. Wtedy jedna ze współrzędnych zapisywana jest za pomocą cyfr arabskich, druga za pomocą znaków rzymskich.
Jednym z najstarszych układów współrzędnych jest układ współrzędnych geograficznych.
Położenie punktu na mapie określa się za pomocą dwóch liczb zwanych szerokością geograficzną i długością geograficzną.
Korzystając z poniższej mapy, połącz w pary miasta i ich współrzędne geograficzne.

Układ współrzędnych jest wykorzystywany nie tylko przy sporządzaniu map (współrzędne geograficzne), ale także w urządzeniach do nawigacji, np. GPS. Zwykły samochodowy GPS podaje współrzędne z dużą dokładnością, można więc bardzo dokładnie wyznaczyć trasę przejazdu do określonego celu.
Punkty skrajne Polski:

Najdalej na północ wysunięty kraniec Polski o współrzędnych – miejscowość Jastrzębia Góra w gminie Władysławowo, powiat pucki.
Najdalej na południe wysunięty kraniec Polski – szczyt Opołonek w gminie Lutowiska, powiat bieszczadzki.
Najdalej na zachód wysunięty kraniec Polski – kolano Odry koło Osinowa Dolnego w gminie Cedynia, powiat gryfiński.
Najdalej na wschód wysunięty kraniec Polski – kolano Bugu we wsi Zosin w gminie Horodło, powiat hrubieszowski.
Środek geometryczny Polski znajduje się we wsi Piątek, na wschód od Łęczycy, na południe od Kutna, a na północ od Łodzi.
Określ współrzędne geograficzne środka Polski.
Jednym z najbardziej tajemniczych miejsc na ziemi jest Trójkąt Bermudzki.
Określ współrzędne geograficzne jego wierzchołków i dowiedz się, czym się charakteryzuje ten obszar. Skorzystaj z Internetu, aby dowiedzieć się, jakie punkty wchodzą w skład Trójkąta Bermudzkiego i odczytaj ich współrzędne z mapy.
Odpowiedź: Różnica wynosi około Tu uzupełnij minut.W Szczecinie jest godzina w południe czasu słonecznego. Która godzina czasu słonecznego jest wtedy w Lublinie?
Odpowiedź: W Lublinie jest godzina Tu uzupełnij:Tu uzupełnij.W Warszawie czas słoneczny określany jest według południka . Jaka jest różnica czasu słonecznego między Warszawą a Rzeszowem?
Odpowiedź: Różnica wynosi Tu uzupełnij minut.
Odpowiednikiem układu współrzędnych na płaszczyźnie jest układ współrzędnych w przestrzeni. Za jego pomocą można opisać na przykład ruch samolotu.
Układ współrzędnych w przestrzeni składa się z trzech wzajemnie prostopadłych osi liczbowych , , . Położenie punktu w przestrzeni określa trójka liczb .
Zbiory punktów w układzie współrzędnych
W układzie współrzędnych można zaznaczać nie tylko poszczególne punkty, ale zbiory punktów, tworzące proste czy półpłaszczyzny.
Uruchom aplet i wykonaj polecenia w nim zawarte.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/D91NVnRlI
Uruchom aplet i wykonaj polecenia w nim zawarte.
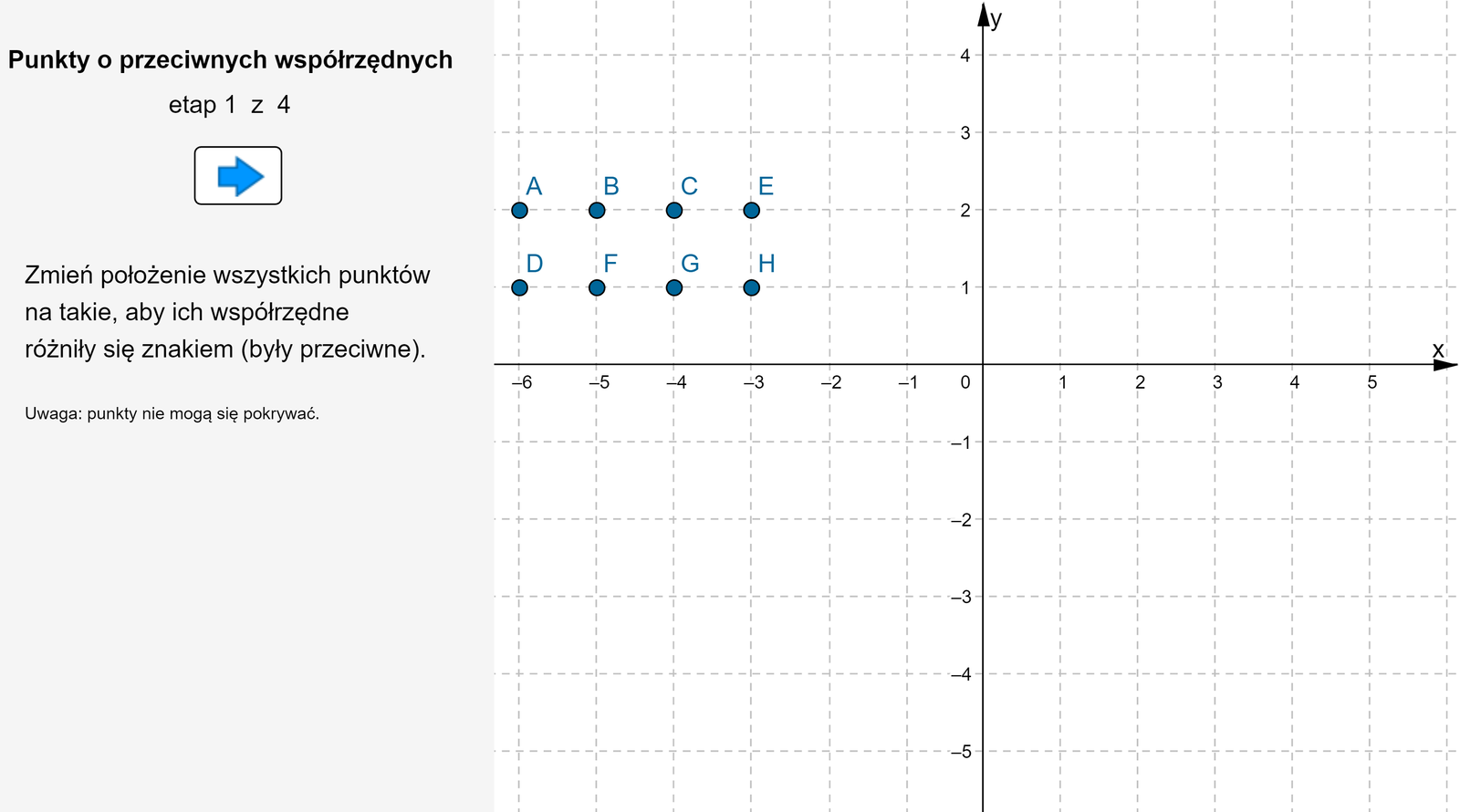
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/D91NVnRlI
Uruchom aplet i wykonaj polecenia w nim zawarte.
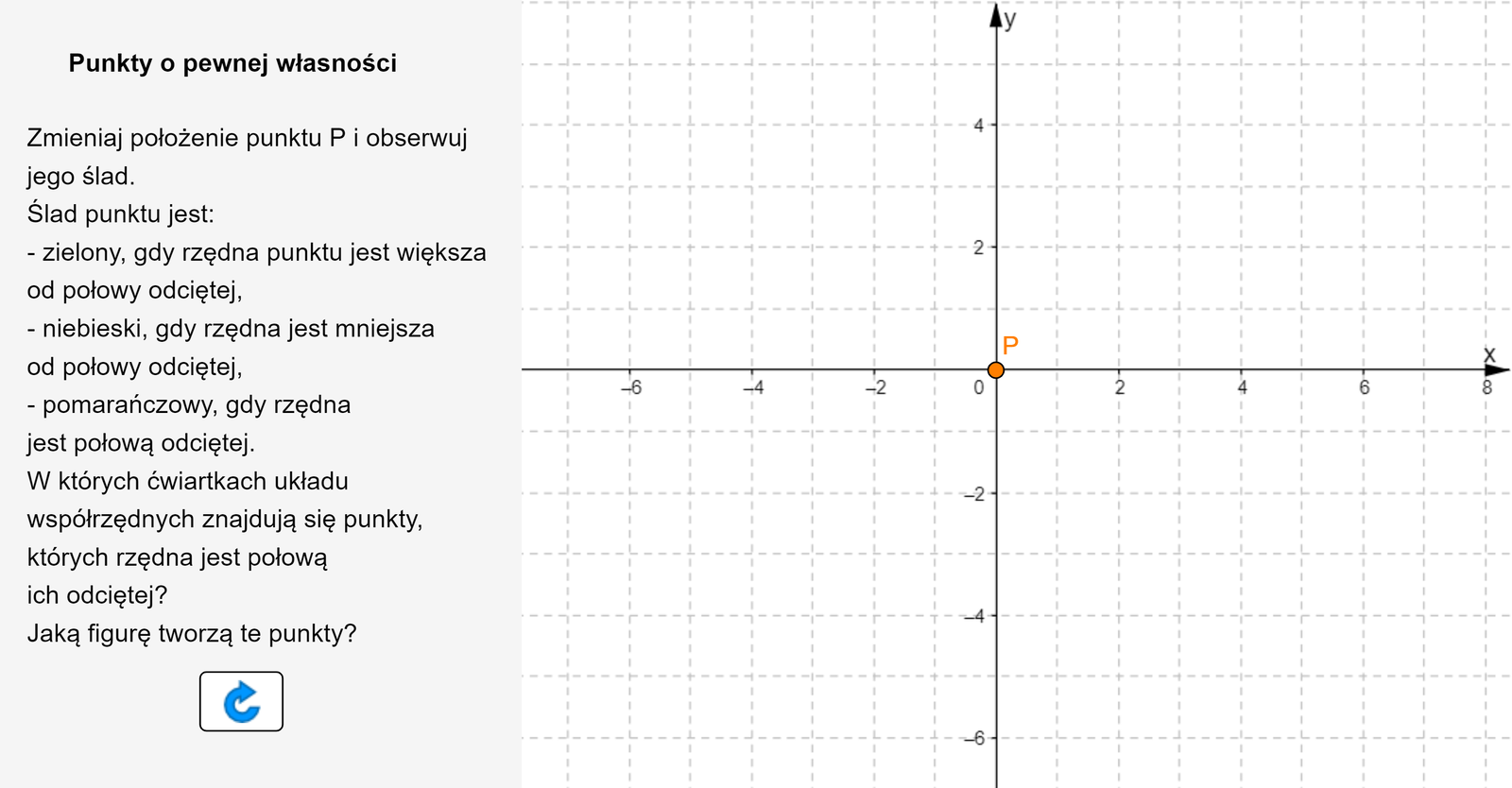
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/D91NVnRlI
Punkty, których druga współrzędna jest połową pierwszej współrzędnej, leżą na prostej. Są to wszystkie punkty takie, że i jest dowolną liczbą rzeczywistą.
Uruchom aplet i wykonaj polecenia w nim zawarte.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/D91NVnRlI
Takie punkty mogą się znaleźć tylko w pierwszej, drugiej i trzeciej ćwiartce układu współrzędnych. Wszystkie takie punkty tworzą prostą o równaniu .
Zaznaczymy w układzie współrzędnych trzy punkty o współrzędnych , gdzie jest dowolną liczbą rzeczywistą.
Zapis oznacza, że pierwsza współrzędna punktu jest dowolna, a druga jest o większa od pierwszej.
Jeśli pierwsza współrzędna punktu będzie równa , to druga jest równa .
Zapisujemy: , . Wtedy .Jeśli pierwsza współrzędna punktu będzie równa , to druga jest równa .
Zapisujemy , . Wtedy .Jeśli pierwsza współrzędna punktu będzie równa , to druga jest równa .
Zapisujemy , . Wtedy .


Zapisz za pomocą wzoru zależność między współrzędnymi punktów zaznaczonych w układzie współrzędnych.

b) Wszystkie punkty leżą na prostej 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8.
Znajdź liczbę , wiedząc, że
punkt leży na osi ,
punkt leży na osi .
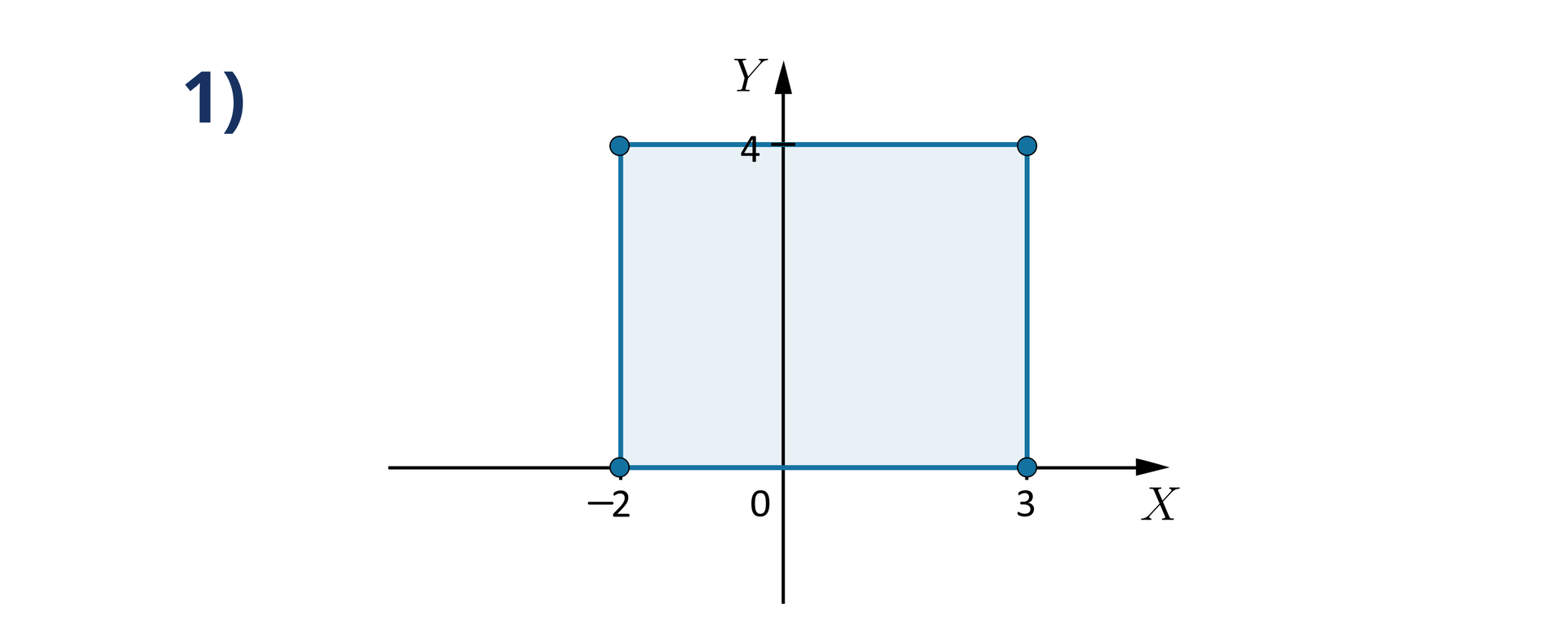
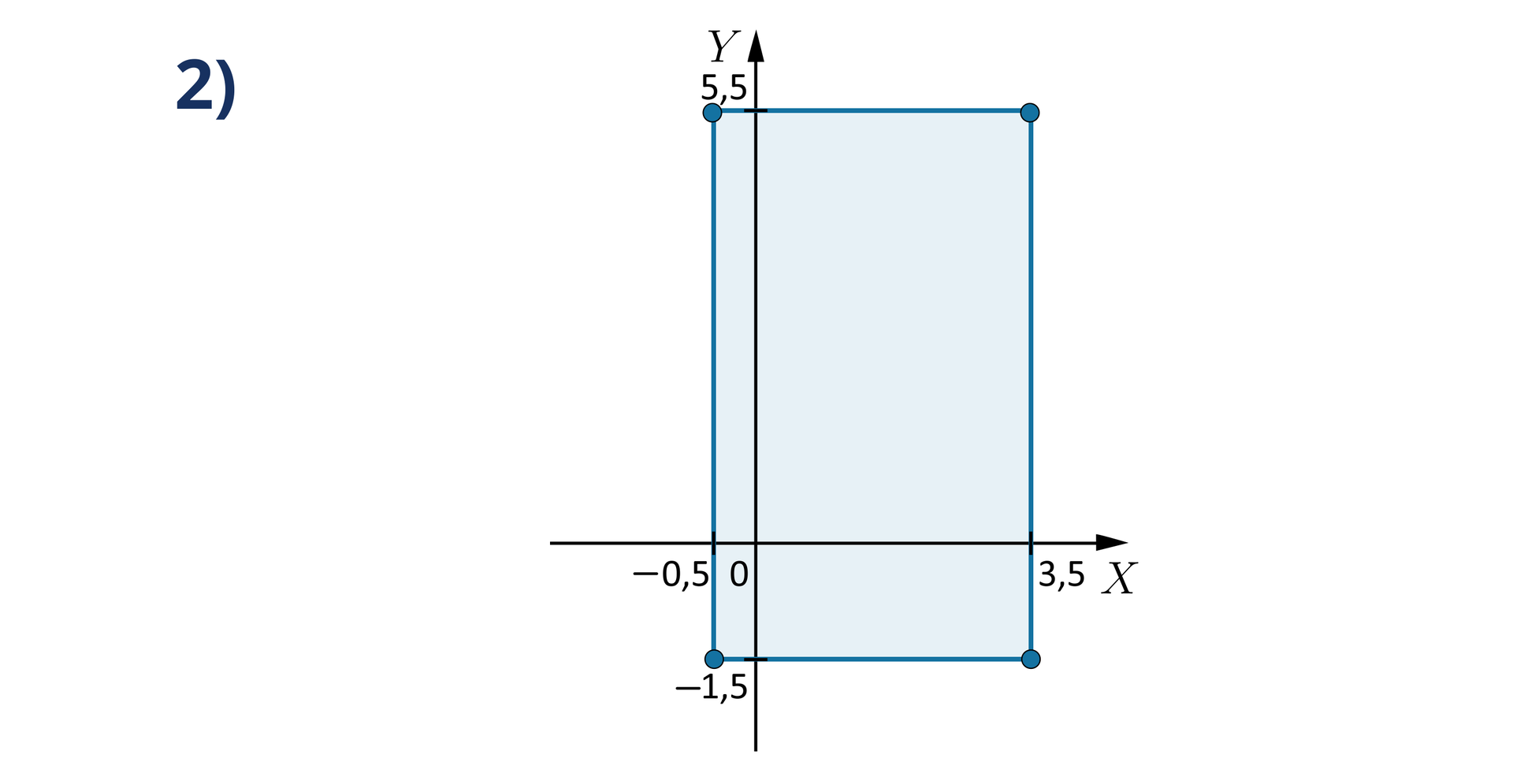
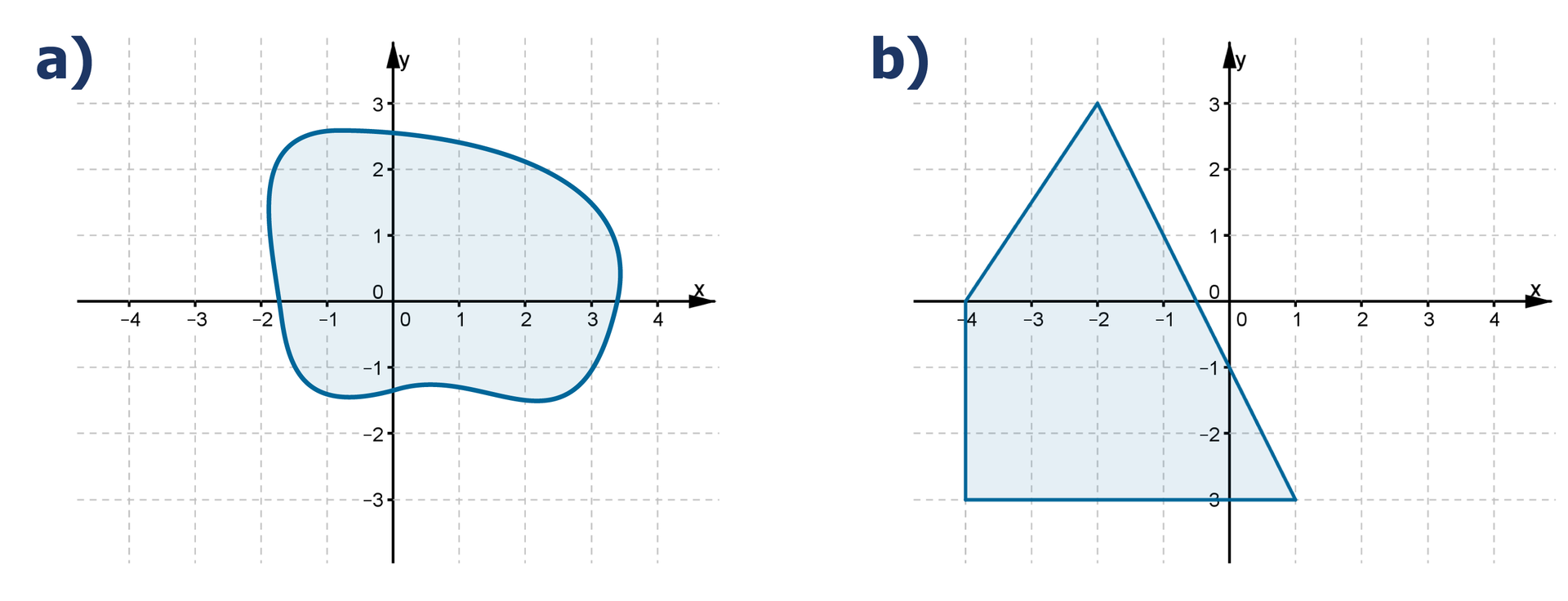
Ile punktów, których obie współrzędne są liczbami całkowitymi, należy do wyróżnionego obszaru?
Umieść podane punkty w odpowiednich miejscach układu współrzędnych. W której ćwiartce układu współrzędnych znajduje się największa liczba punktów, a w której najmniejsza?
Zastanów się w których miejscach układu współrzędnych leżą poniższe punkty. W której ćwiartce układu współrzędnych znajduje się największa liczba punktów, a w której najmniejsza?
Podane jest punktów:
Na poniższym układzie współrzędnych dobierz odpowiednią jednostkę, i zaznacz w nim punkty:
Zastanów się, w których miejscach w układzie współrzędnych leżą punkty:
.
Wypisz punkty
leżące na osi rzędnych
leżące na osi odciętych
których współrzędne są liczbami przeciwnymi
należące do , , i ćwiartki układu współrzędnych
Zaznacz w układzie współrzędnych taki punkt, którego suma współrzędnych jest równa . Zaznacz jeszcze takich punktów. Jaka jest zależność między pierwszą a drugą współrzędną każdego z punktów?
Znajdź takie punkty, których suma współrzędnych jest równa . Podaj przykład siedmiu takich punktów. Jaka jest zależność między pierwszą a drugą współrzędną każdego z punktów?
- w lub w ćwiartce układu współrzędnych
- w lub w ćwiartce układu współrzędnych
- w lub w ćwiartce układu współrzędnych
- w lub w ćwiartce układu współrzędnych
Narysuj układ współrzędnych i zaznacz w nim poniższe punkty.
Zastanów się, w których miejscach w układzie współrzędnych leżą punkty:
, , ,
, , ,
, , , .
Zaznacz w układzie współrzędnych punkt taki, że
Podaj współrzędne punktu takiego, że
,
,
,
,
Zaznacz w układzie współrzędnych punktów spełniających podany warunek. Na jakiej prostej leżą wszystkie te punkty?
Podaj współrzędne pięciu punktów spełniających podany warunek. Na jakiej prostej leżą wszystkie te punkty?
Pierwsza współrzędna jest dwukrotnie mniejsza od drugiej.
Druga współrzędna jest równa .
Pierwsza współrzędna jest równa .
Zaznacz w układzie współrzędnych zbiór punktów , których współrzędne spełniają podany warunek.
i
i
Zapoznaj się z poniższym rysunkiem.
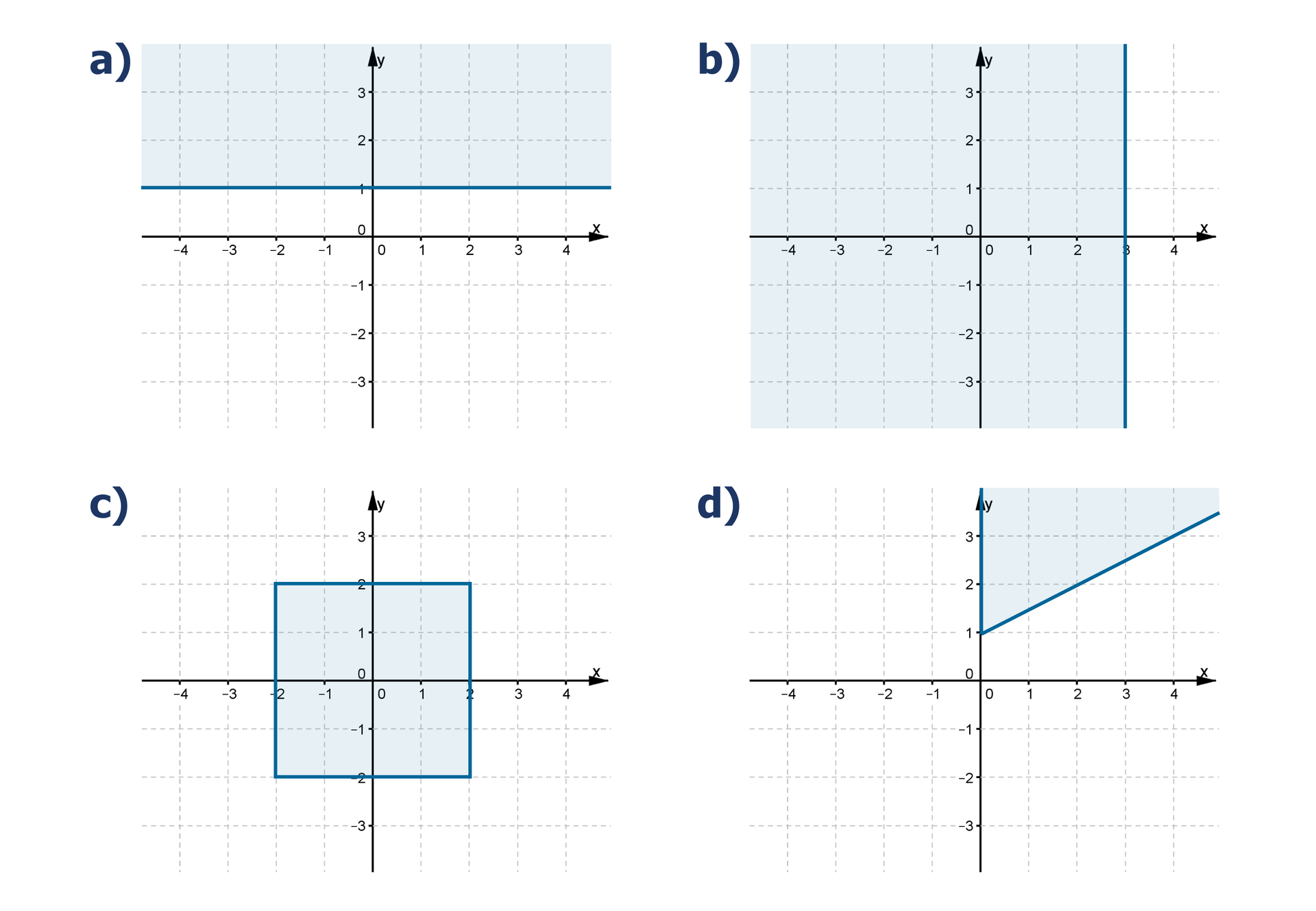
Wyznacz współrzędne punktów znajdujących się na odcinku , gdzie , .
Notatnik
Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.