Rachunek prawdopodobieństwa
3. Obliczanie prawdopodobieństwa zdarzeń
Czy wiesz, że w ruletkę grali już starożytni Grecy? Nowoczesną ruletkę wymyślił w r. nie kto inny jak matematyk – Blaise Pascal. Ruletka zwana jest też szatańską grą, bo suma wszystkich liczb w ruletce daje .
Badania nad możliwością wygranych w grach hazardowych, prowadzone miedzy innymi przez Pascala, przyczyniły się do powstania dziedziny matematyki, którą dzisiaj nazywamy rachunkiem prawdopodobieństwa.

W r. francuski polityk i historyk Louis Blac wraz z bratem Francisem dołożyli do ruletki, aby zwiększyć szanse wygrania kasyna. Założyli też pierwsze kasyno w Monako.
W ruletce, inaczej niż w innych grach hazardowych, dość łatwo obliczyć szansę trafienia konkretnego numeru.
Więc warto zgłębić tajniki rachunku prawdopodobieństwa, a w szczególności sposób określania liczby zdarzeń elementarnych oraz liczby zdarzeń sprzyjających dla danego doświadczenia losowego. Bo może i Ty kiedyś pojedziesz do Monako ...
Na początku przypomnijmy definicję doświadczenia losowego.
Zjawisko losowe, które można powtarzać wiele razy w tych samych warunkach, ale jego kolejnych wyników nie potrafimy przewidzieć nazywamy doświadczeniem losowym.
Doświadczeniami losowymiDoświadczeniami losowymi mogą być np. rzut kostką do gry, rzut monetą, losowanie kart z talii. Z pojęciem tym związane jest zdarzenie elementarne, którego nie definiuje się (jest to tzw. pojęcie pierwotne w teorii prawdopodobieństwa).
Po przeprowadzeniu doświadczenia losowego możemy wyznaczyć częstość występowania poszczególnych wyników. W taki sposób obliczamy prawdopodobieństwo zdarzenia.
Prawdopodobieństwem zdarzenia nazywamy szansę na wystąpienie danego zdarzenia.
Wprowadźmy następujące oznaczenia:
– liczba zdarzeń elementarnych sprzyjających danemu zdarzeniu,
– liczba wszystkich zdarzeń elementarnych,
– prawdopodobieństwo zdarzenia.
Wówczas prawdopodobieństwo zdarzenia obliczamy ze wzoru:
Rzucamy dwukrotnie symetryczną czworościenną kostką do gry. Obliczymy, jakie jest prawdopodobieństwo, że suma wyrzuconych oczek jest równa co najmniej .
Rozwiązanie:
Przedstawmy w tabeli zbiór wszystkich wyników omawianego doświadczenia losowego:
Zauważmy, że liczba wszystkich wyników doświadczenia losowego jest równa .
Wypisujemy zdarzenia sprzyjające temu, że suma wyrzuconych oczek jest równa co najmniej : , , , , , .
Wobec tego:
Prawdopodobieństwo omawianego zdarzenia jest równe:
.
Rzucamy jeden raz symetryczną czworościenną kostką do gry, a następnie jeden raz symetryczną sześcienną kostką do gry. Obliczymy prawdopodobieństwo zdarzenia:
suma oczek wyrzuconych na obu kostkach jest podzielna przez ,
iloczyn wyrzuconych oczek jest podzielny przez ,
iloraz liczby oczek na drugiej kostce przez liczbę oczek otrzymanych na pierwszej kostce jest liczbą naturalną.
Rozwiązanie:
Przedstawmy w tabeli zbiór możliwych rozwiązań doświadczenia losowego:
Liczba | ||||||
|---|---|---|---|---|---|---|
Zauważmy, że liczba wszystkich możliwych zdarzeń w tym doświadczeniu losowym wynosi .
Pary liczb, których suma jest podzielna przez : , , , , , .
Wobec tego:
,Pary liczb, których iloczyn jest podzielny przez : , , , .
Wobec tego:
,Pary liczb, których iloraz drugiej liczby przez pierwszą jest liczbą naturalną: , , , , , , , , , , , .
Wobec tego:
.
W pojemniku znajdują się losy wygrywające i przegrywających. Losujemy dwa razy ze zwracaniem po jednym losie. Obliczymy prawdopodobieństwo zdarzenia:
wylosowano najpierw los przegrywający, a następnie los wygrywający,
wylosowano co najmniej jeden los wygrywający.
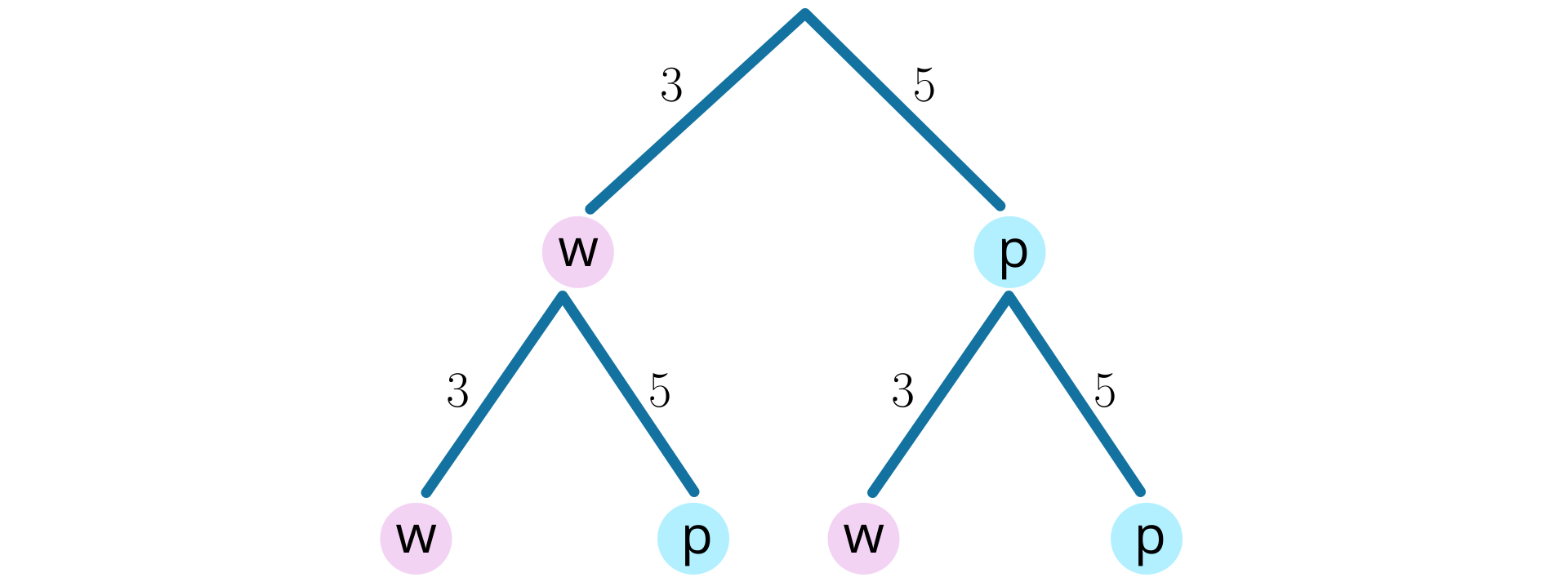
Schemat. W poniższym schemacie przedstawiono drzewko stochastyczne ilustrujące możliwości wylosowania losu wygrywającego i wylosowania losu przegrywającego w dwóch kolejnych losowaniach ze zwracaniem. Literą W oznaczono sytuację, w której wylosowano los wygrywający, natomiast literą P oznaczono sytuację, w której wylosowano los wygrywający. Lista elementów:
Nazwa kategorii: START
Elementy należące do kategorii STARTNazwa kategorii: W ( losowanie)
Elementy należące do kategorii W ( losowanie)Nazwa kategorii: W ( losowanie)
Nazwa kategorii: P ( losowanie)
Nazwa kategorii: P ( losowanie)
Elementy należące do kategorii P ( losowanie)Nazwa kategorii: W ( losowanie)
Nazwa kategorii: P ( losowanie)
Zatem liczba wszystkich wyników tego doświadczenia losowego jest równa:
. Wówczas:
,
.
Doświadczenie losowe polega na trzykrotnym rzucie symetryczną monetą. Obliczymy prawdopodobieństwo zdarzenia polegającego na wyrzuceniu liczby orłów mniejszej niż liczby reszek.
Rozwiązanie:
Narysujmy drzewo doświadczenia losowego.
Schemat. W poniższym schemacie przedstawiono drzewo stochastyczne ilustrujące możliwości wyrzucenia orła i reszki w trzech kolejnych rzutach. Literą O oznaczono sytuację, w której wyrzucono orła, natomiast literą R oznaczono sytuację, w której wyrzucono reszkę.
Nazwa kategorii: START
Elementy należące do kategorii STARTNazwa kategorii: O ( losowanie)
Elementy należące do kategorii O ( losowanie)Nazwa kategorii: O ( losowanie) Elementy należące do kategorii O ( losowanie)
Nazwa kategorii: O ( losowanie)
Nazwa kategorii: R ( losowanie)
Nazwa kategorii: R ( losowanie) Elementy należące do kategorii R ( losowanie)
Nazwa kategorii: O ( losowanie)
Nazwa kategorii: R ( losowanie)
Nazwa kategorii: R ( losowanie)
Elementy należące do kategorii R ( losowanie)Nazwa kategorii: O ( losowanie) Elementy należące do kategorii O ( losowanie)
Nazwa kategorii: O ( losowanie)
Nazwa kategorii: R ( losowanie)
Nazwa kategorii: R ( losowanie) Elementy należące do kategorii R ( losowanie)
Nazwa kategorii: O ( losowanie)
Nazwa kategorii: R ( losowanie)
Nazwa kategorii: R ( losowanie)
Wypisujemy zdarzenia sprzyjające zdarzeniu, w którym liczba orłów jest mniejsza niż liczba reszek: , , , .
Zatem , , wobec tego prawdopodobieństwo zdarzenia polegającego na wyrzuceniu liczby orłów mniejszej niż liczby reszek jest równe:
.
Rzucamy dwukrotnie symetryczną sześcienną kostką do gry. Obliczymy prawdopodobieństwo zdarzenia:
iloczyn wyrzuconych oczek jest większy niż ,
suma wyrzuconych oczek jest nie mniejsza niż .
Rozwiązanie:
Jeżeli dwukrotnie rzucamy symetryczną sześcienną kostką do gry, to liczba wszystkich wyników tego doświadczenia jest równa .
Zauważmy, że jest sześć możliwości, gdy iloczyn wyrzuconych oczek jest większy niż : , , , , , .
Wobec tego:
,Jeżeli suma wyrzuconych oczek jest nie mniejsza niż , to suma ta wynosi lub . Zatem mamy następujące możliwości: , ,
Wobec tego:
.
Prawdopodobieństwo zdarzenia możemy obliczyć również w przypadku doświadczenia losowego, w którym występuje losowanie bez zwracania lub stosujemy regułę mnożenia.
Z urny zawierającej kule ponumerowane liczbami od do losujemy bez zwracania dwie kule. Obliczymy prawdopodobieństwo tego, że suma liczb na wylosowanych kulach będzie nie większa niż .
Rozwiązanie:
Przedstawmy za pomocą tabeli zbiór wszystkich par liczb, które otrzymujemy w wyniku doświadczenia.
Liczba | ||||||
|---|---|---|---|---|---|---|
Zauważmy, że wszystkich par liczb jest .
Wypisujemy pary liczb, których suma będzie nie większa niż : , , , , , , , .
Jest takich par liczb.
Wobec tego , oraz prawdopodobieństwo tego, że suma liczba na wylosowanych kulach będzie nie większa niż wynosi:
.
Pani Joanna zamierza zjeść w restauracji obiad złożony z zupy i dania głównego. Obliczymy prawdopodobieństwo tego, że wybierze:

zupę fasolową i danie mięsne,
dowolną zupę i drugie danie bezmięsne.
Rozwiązanie:
Obliczamy ilość wszystkich zestawów obiadowych, złożonych z zupy i dania głównego:
.
Obliczamy liczbę zdarzeń sprzyjających zdarzeniu: wybrano zupę fasolową i danie mięsne.
Obliczamy prawdopodobieństwo zdarzenia:
,Obliczamy liczbę zdarzeń sprzyjających zdarzeniu: wybrano dowolną zupę i danie bezmięsne.
Obliczamy prawdopodobieństwo zdarzenia:
.
Ilustracja interaktywna
Zapoznaj się z ilustracją interaktywną, a następnie wykonaj poniższe polecenia.
Rzucamy dwukrotnie symetryczną kostką do gry. Obliczamy prawdopodobieństwo zdarzenia, w którym liczba oczek w pierwszym rzucie jest o trzy większa niż liczba oczek w drugim rzucie.
Etap pierwszy:
Przedstawiamy za pomocą tabeli zbiór wszystkich par liczb, które otrzymujemy w wyniku doświadczenia, a następnie obliczamy liczbę wszystkich możliwych zdarzeń.
Liczba | ||||||
|---|---|---|---|---|---|---|
Liczba wszystkich możliwych zdarzeń w tym doświadczeniu losowym wynosi .
Etap drugi:
Wyznaczamy liczbę zdarzeń, w których liczba oczek w pierwszym rzucie jest o trzy większa niż liczba oczek w drugim rzucie.
Pary liczb, w których pierwsza liczba jest o trzy większa od drugiej to: , .
Oznacza to, że istnieją dokładnie trzy zdarzenia, w których liczba oczek w pierwszym rzucie jest o trzy większa niż liczba oczek w drugim rzucie.
Etap trzeci:
Obliczamy prawdopodobieństwo zdarzenia korzystając z odpowiedniego wzoru.
Prawdopodobieństwo zdarzenia, w którym liczba oczek w pierwszym rzucie jest o trzy większa niż liczba oczek w drugim rzucie wynosi .
Rzucamy dwukrotnie symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że na obu kostkach wypadła liczba pierwsza.
Rzucamy dwukrotnie symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że suma wyrzuconych oczek jest podzielna przez .
Rzucamy dwukrotnie symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że iloczyn wyrzuconych oczek jest kwadratem liczby naturalnej dodatniej.
Gra edukacyjna
Zagraj w grę, a następnie wykonaj poniższe polecenia.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DDqhzZ9gM
Gra edukacyjna - Obliczanie prawdopodobieństwa zdarzeń.
Gra składa się z trzech poziomów. Na każdym poziomie jest sześć pytań. W każdym pytaniu tylko jedna poprawna odpowiedź.
Rzucamy czterokrotnie symetryczną monetą. Oblicz prawdopodobieństwo tego, że wypadły co najmniej trzy orły.
Rozwiąż zadania:
Pani Zuzanna ma do dyspozycji: różne pary butów, różne sukienki i różnych torebek. Wybiera zestaw składający się z pary butów, sukienki i torebki. Jakie jest prawdopodobieństwo wybrania ustalonego zestawu spośród wszystkich możliwych wyborów?
Pan Grzegorz ma marynarki, różnych par spodni oraz różnych koszul. Wybiera zestaw składający się z marynarki, spodni i koszuli. Jakie jest prawdopodobieństwo wyboru ustalonego zestawu spośród wszystkich możliwych wyborów?
Ustal prawdopodobieństwo następującego zdarzenia: dwukrotne wyrzucenie orła w trzykrotnym rzucie symetryczną monetą.
Zestaw ćwiczeń interaktywnych
Prawdopodobieństwo zdarzenia, że wylosowano liczby, których iloczyn jest parzysty jest równe 1. , 2. , 3. , 4. , 5. , 6. .
Prawdopodobieństwo zdarzenia, że obie wylosowane liczby są równe wynosi 1. , 2. , 3. , 4. , 5. , 6. .
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzeń:
liczba oczek w drugim rzucie jest razy większa niż liczba oczek w pierwszym rzucie,
iloczyn liczby otrzymanych oczek przy dzieleniu przez daje resztę .
W urnie znajdują się kule czerwone i niebieskie. Losujemy dwie kule ze zwracaniem. Jakie jest prawdopodobieństwo zdarzenia, że wylosowaliśmy co najmniej jedną kulę czerwoną?
Pani Kasia chce zamówić w herbaciarni kawę i ciasto. Oblicz prawdopodobieństwo tego, że wybierze:

herbatę cytrynową i makowiec lub sernik,
herbatę truskawkową i dowolne ciasto.
Słownik
doświadczenie, które można powtarzać wiele razy w tych samych warunkach, ale jego kolejnych wyników nie potrafimy przewidzieć
Notatnik
Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.