Wielokąty, koła i okręgi
6. Własności rombu
Na rysunkach poniżej, pierwszy od lewej przedstawia fragment posadzki, drugi – fragment mozaiki z oferty sprzedażowej kafelków do łazienek, a na trzecim obrazku jest fragment dywanu. Co łączy te obrazki?

Otóż wzory na wszystkich tych obrazkach powstały z ułożenia rombów i odpowiedniego ich pokolorowania.
W tym materiale dowiesz się, jakie czworokąty nazywamy rombami. Poznasz własności tych figur. Swoją wiedzę sprawdzisz rozwiązując ćwiczenia.
Poznajemy romb
Film dostępny pod adresem /preview/resource/RYKsRoHv2Z76g
Animacja przedstawia w jaki sposób z prostokątnej kartki papieru otrzymać romb.
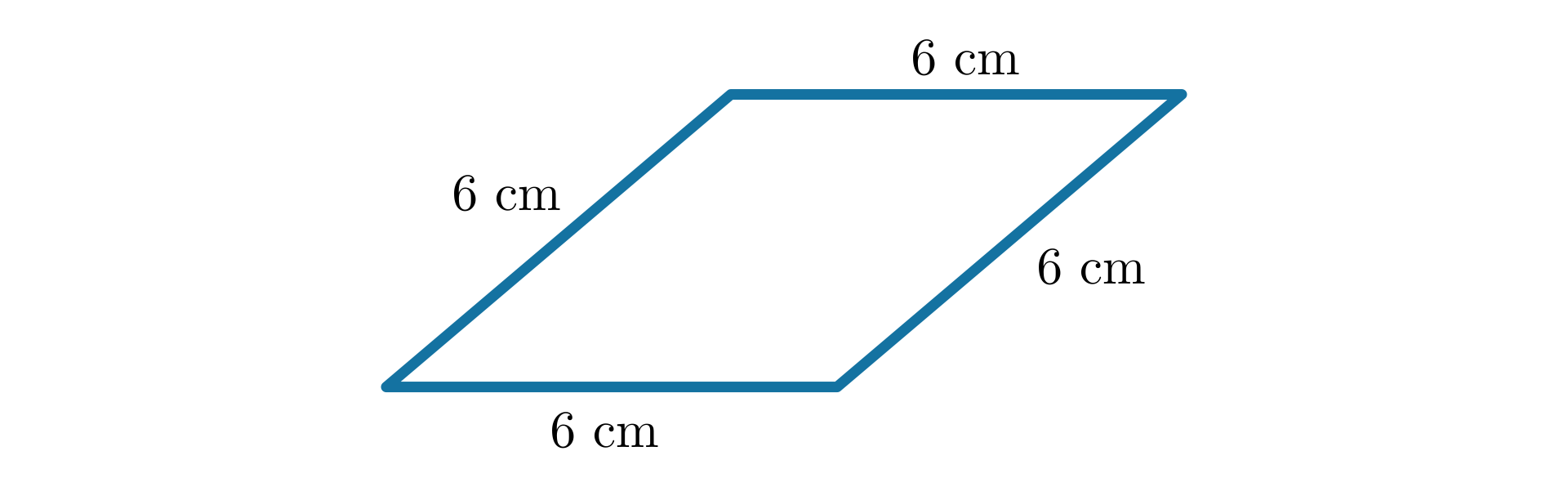
Romb to równoległobok o bokach równej długości.

Własności rombu
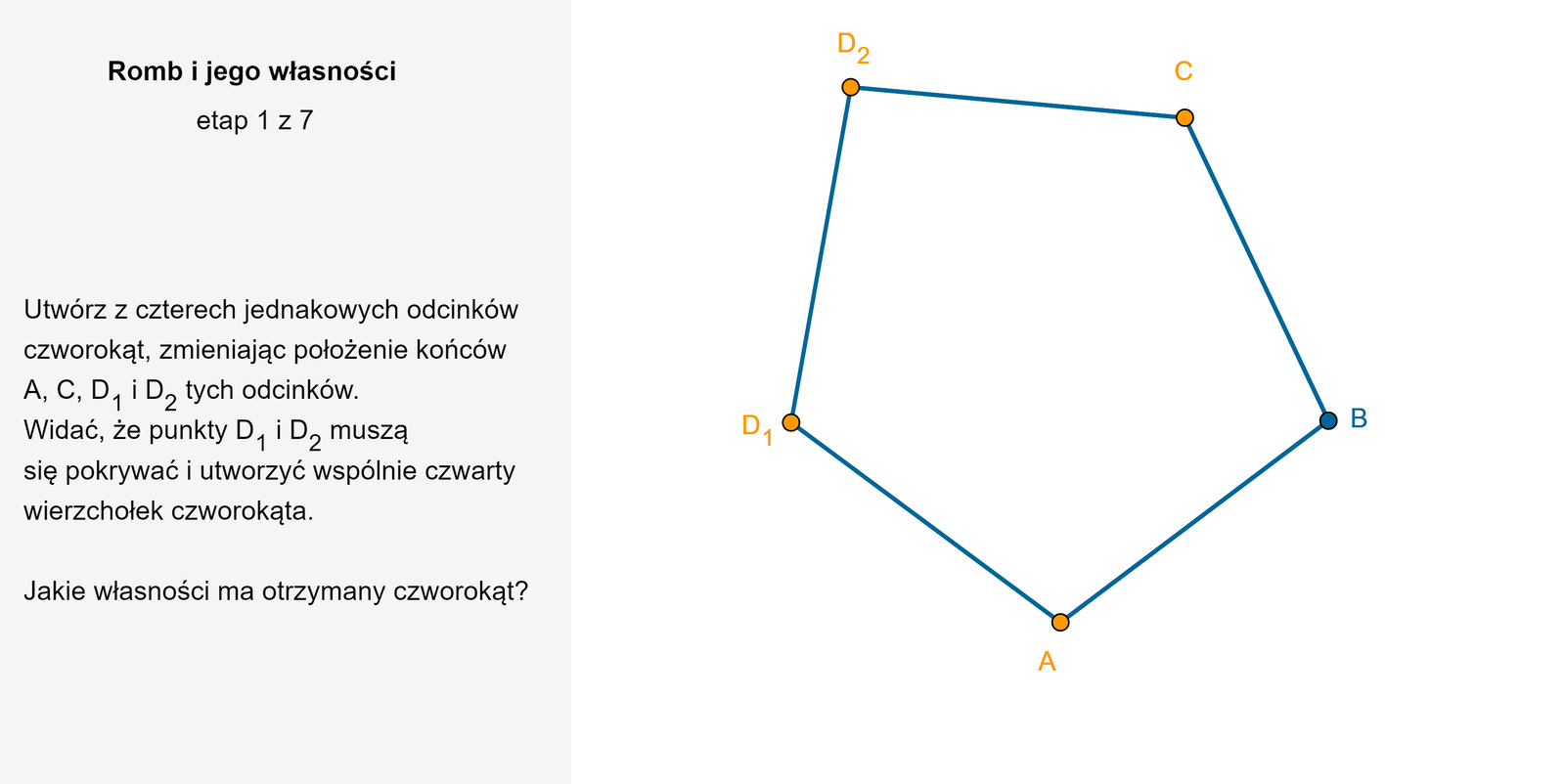
Zapoznaj się z poniższym apletem i informacjami pod nim.
Zapoznaj się z opisem poniższego apletu i informacjami pod nim.
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DIb7O666i
W każdym rombie wszystkie boki są równej długości.
W każdym rombie przeciwległe kąty mają równe miary. Suma miar sąsiednich kątów wynosi .
R1L6QvYWgDHda1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.W każdym rombie przekątne dzielą się na połowy i przecinają pod kątem prostym.
RVrH4v4olIV251 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Zapoznaj się z poniższym apletem i wykonaj polecenia.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DIb7O666i
W otrzymanym czworokącie: wszystkie boki są 1. równoległe, 2. dzielą się, 3. równej długości, 4. , 5. równe miary, 6. nie dzielą się, 7. prostopadłe, 8. różnej długości, 9. równoległe, 10. , 11. , 12. prostopadłe, 13. różne miary,przeciwległe boki są 1. równoległe, 2. dzielą się, 3. równej długości, 4. , 5. równe miary, 6. nie dzielą się, 7. prostopadłe, 8. różnej długości, 9. równoległe, 10. , 11. , 12. prostopadłe, 13. różne miary,przeciwległe kąty mają 1. równoległe, 2. dzielą się, 3. równej długości, 4. , 5. równe miary, 6. nie dzielą się, 7. prostopadłe, 8. różnej długości, 9. równoległe, 10. , 11. , 12. prostopadłe, 13. różne miary,suma miar dwóch sąsiednich kątów wynosi 1. równoległe, 2. dzielą się, 3. równej długości, 4. , 5. równe miary, 6. nie dzielą się, 7. prostopadłe, 8. różnej długości, 9. równoległe, 10. , 11. , 12. prostopadłe, 13. różne miary,przekątne są do siebie 1. równoległe, 2. dzielą się, 3. równej długości, 4. , 5. równe miary, 6. nie dzielą się, 7. prostopadłe, 8. różnej długości, 9. równoległe, 10. , 11. , 12. prostopadłe, 13. różne miary,przekątne 1. równoległe, 2. dzielą się, 3. równej długości, 4. , 5. równe miary, 6. nie dzielą się, 7. prostopadłe, 8. różnej długości, 9. równoległe, 10. , 11. , 12. prostopadłe, 13. różne miary na połowy.
Wybierz.
W otrzymanym czworokącie
prostopadłe, nie dzielą się, równe miary, 360, prostopadłe, różnej długości, równoległe, różne miary, dzielą się, równej długości, równoległe, 180, 90
a) wszystkie boki są ......................................
b) przeciwległe boki są ......................................
c) przeciwległe kąty mają ......................................
d) suma miar dwóch sąsiednich kątów wynosi ...................................... °
e) przekątne są do siebie ......................................
f) przekątne ...................................... na połowy
Które z poniższych czworokątów są rombami?

Narysuj romb, którego bok ma długość . Oblicz obwód tego rombu.
Dany jest romb, którego bok ma długość . Oblicz obwód tego rombu.
Narysuj romb o przekątnych długości i . Zmierz długość jego boku i oblicz obwód rombu.
Dany jest romb, którego bok ma długość . Oblicz obwód tego rombu.
Uzupełnij.
Romb o obwodzie
a) 36 cm ma bok długości ............ cm
b) 6 dm ma bok długości ............ cm
c) 7 m ma bok długości ............ cm
Figury na poniższych rysunkach zbudowano z trójkątów równobocznych. Ile różnych rombów można wyróżnić na każdym rysunku? Uzupełnij luki, wpisując odpowiednie liczby.
Notatnik
Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.