Przeczytaj

Zastosowanie twierdzenia o odcinkach stycznych

Rozważania zaczniemy od prostej konsekwencji zasadniczego twierdzenia planimetrii, z której będziemy korzystać przy rozwiązywaniu kolejnych problemów.

O stycznych do dwóch okręgów

Twierdzenie: O stycznych do dwóch okręgów

Niech $P Q$ i $R S$ będą odcinkami wyznaczonymi przez punkty, w których dwa okręgi są odpowiednio styczne do ich wspólnych stycznych zewnętrznych, jak na rysunku.

REXwurZT97Ud0

Na ilustracji przedstawiono dwa okręgi obok siebie. Większy okrąg niebieski, oraz mniejszy granatowy. Poprowadzono dwie proste. Pierwsza prosta, jest styczna do okręgu niebieskiego w punkcie P, oraz styczna do okręgu granatowego w punkcie Q. Druga prosta jest styczna do okręgu niebieskiego w punkcie R, oraz do okręgu granatowego w punkcie S. Różowym kolorem zaznaczono odcinek PQ oraz RS.

Wtedy $|P Q| = |R S|$ .

Dowód

Zauważmy, że w przypadku równości promieni, wspólne styczne zewnętrzne obu okręgów byłyby równoległe, a czworokąt $P R S Q$ byłby prostokątem. Teza twierdzenia byłaby wówczas oczywista. Przypuśćmy więc, że promienie są różne. Wtedy proste $P Q$ i $R S$ przetną się – ich punkt wspólny oznaczmy przez $M$ . Nie zmniejszając ogólności, możemy przyjąć (jak sugeruje rysunek), że punkt $Q$ leży pomiędzy punktami $P$ i $M$ . Wtedy $|M P| = |M Q| + |P Q|$ oraz $|M R| = |M S| + |R S|$ . Z twierdzenia o odcinkach stycznych wynika, że $|M Q| = |M S|$ oraz $|M P| = |M R|$ . Stąd $|M S| + |R S| = |M R| = |M P| = |M Q| + |P Q| = |M S| + |P Q|$ , zatem $|P Q| = |R S|$ .

Przykład 1

Rozważmy dwa okręgi. Punkty $A$ i $C$ leżą odpowiednio na jednej z dwóch wspólnych stycznych zewnętrznych do tych okręgów, w taki sposób, że odcinek $A C$ jest zawarty w jednej ze wspólnych stycznych wewnętrznych do tych okręgów, jak na rysunku.

RBDnXqMHUR4sF

Na ilustracji przedstawiono dwa okręgi. Poprowadzono dwie styczne, które są wspólne dla obu okręgów. Styczne połączono prostą AC, która przechodzi między okręgami i jest styczna do okręgu pierwszego w punkcie D, oraz do styczna do okręgu drugiego w punkcie B.

Pokażemy, że $|A B| = |C D|$ .

W tym celu zaznaczymy odpowiednio punkty styczności.

RU7gSgyxxfxvx

Na ilustracji przedstawiono dwa okręgi. Poprowadzono dwie proste. Pierwsza prosta jest styczna do okręgu pierwszego w punkcie P, i do drugiego w punkcie Q. Druga prosta jest styczna do pierwszego okręgu w punkcie R, i do drugiego w punkcie S. Styczne połączono prostą AC, która przechodzi między okręgami i jest styczna do okręgu pierwszego w punkcie D, oraz do styczna do okręgu drugiego w punkcie B. — Dowód równości odcinków stycznych

Z wcześniejszego twierdzenia wynika, że $|P Q| = |R S|$ , czyli $|A P| + |A Q| = |C S| + |C R|$ . Ale z twierdzenia o odcinkach stycznych (zasadniczego twierdzenia planimetrii) otrzymujemy w szczególności, że $|R C| = |C D|$ , $|C S| = |C B|$ , $|A Q| = |A B|$ oraz $|A P| = |A D|$ . Stąd, wynikającą z twierdzenia o stycznych do dwóch okręgów równość możemy zapisać w postaci $|A D| + |A B| = |C B| + |C D|$ . Pozostaje jeszcze zauważyć, że $|C B| = |C D| + |B D|$ oraz $|A D| = |A B| + |B D|$ , zatem równość $|A D| + |A B| = |C B| + |C D|$ przyjmuje postać $|A B| + |B D| + |A B| = |C D| + |B D| + |C D|$ . Stąd $2 |A B| = 2 |C D|$ , czyli $|A B| = |C D|$ .

Przykład 2

Rozważmy dwa okręgi. Każdy z punktów $A$ i $C$ leży na innej z dwóch wspólnych stycznych wewnętrznych do tych okręgów, które to styczne przecinają wspólną styczną zewnętrzną $R S$ w punktach odpowiednio $B$ i $D$ , jak na rysunku.

RThLaQAb1gonb

Na ilustracji przedstawiono dwa okręgi. Poprowadzono prostą L, styczną do okręgu pierwszego w punkcie R i do okręgu drugiego w punkcie S. Między okręgami poprowadzono dwie proste, styczne do obu okręgów, przecinające się wzajemnie w punkcie M. Zaznaczono punkt styczności A do okręgu pierwszego, oraz punkt styczności C do okręgu drugiego. Prosta L jest przecięta przez styczne w punkcie B i D. Różowym kolorem zaznaczono odcinek AB oraz CD.

Pokażemy, że $|A B| = |C D|$ .

Podobnie, jak w Przykładzie 1. zaczniemy od oznaczenia widocznych na rysunku punktów styczności i punktu $M$ – wspólnego dla stycznych wewnętrznych.

RtDaiyR2Cn4Ha

Na ilustracji przedstawiono dwa okręgi. Poprowadzono prostą P, styczną do okręgu pierwszego w punkcie R i do okręgu drugiego w punkcie S. Między okręgami dwie proste, styczne do obu okręgów, przecinające się wzajemnie w punkcie M. Pierwsza z nich jest styczna do okręgu pierwszego w punkcie P, i do okręgu drugiego w punkcie C. Druga z nich jest styczna do okręgu pierwszego w punkcie A i do okręgu drugiego w punkcie Q. Prosta L jest przecięta przez styczne w punkcie B i D. Różowym kolorem zaznaczono odcinek AB oraz CD. — Dowód równości odcinków stycznych.

Mamy wówczas, że $|D P| = |C D| + |C M| + |M P|$ oraz $|D R| = |B D| + |B R|$ . Podobnie $|B Q| = |A B| + |A M| + |M Q|$ oraz $|B S| = |B D| + |D S|$ . Z twierdzenia o odcinkach stycznych poprowadzonych z punktu $D$ oraz z punktu $B$ otrzymujemy w szczególności, że $|C D| + |C M| + |M P| = |B D| + |B R|$ oraz $|A B| + |A M| + |M Q| = |B D| + |D S|$ . Odejmując stronami ostatnie równości dostajemy, że $|C D| + |C M| + |M P| - (|A B| + |A M| + |M Q|) = |B D| + |B R| - (|B D| + |D S|)$ . Z twierdzenia o odcinkach stycznych otrzymujemy ponadto, że $|P M| = |A M|$ , $|C M| = |M Q|$ , $|B R| = |A B|$ oraz $|D S| = |C D|$ , zatem powyższa równość przyjmuje postać $|C D| + |M Q| + |A M| - (|A B| + |A M| + |M Q|) = |B D| + |A B| - (|B D| + |C D|)$ . Po uproszczeniu i redukcji wyrazów podobnych mamy $|C D| - |A B| = |A B| - |C D|$ , czyli $2 |A B| = 2 |C D|$ , a stąd $|A B| = |C D|$ .

Potęga punktu względem okręgu

Rozważmy okrąg o środku w punkcie $O$ i punkt $P$ leżący na zewnątrz okręgu. Z tego punktu poprowadźmy styczną oraz sieczną tego okręgu, jak na rysunku.

RX8iymGhzk0Q9

Na ilustracji przedstawiono okrąg o środku w punkcie O. Poprowadzono prostą, styczną do okręgu w punkcie A, oraz prostą przecinającą okrąg w punkcie Q i R. Proste przecinają się w punkcie P. — Styczna i sieczna

Niech $A$ będzie punktem styczności, a $Q$ , $R$ będą punktami, w których sieczna przecina dany okrąg. Okazuje się, że $|P Q| \cdot |P R| = {|P A|}^{2}$ niezależnie od wyboru siecznej.

Dla dowodu pokażemy, że trójkąty $P R A$ i $P A Q$ są podobne. Skorzystamy w tym celu z twierdzenia o kącie wpisanym i środkowym opartych na tym samym łuku i z faktu, że promień $O A$ jest prostopadły do stycznej $A P$ .

R8T3Cw9pMmDX0

Oznaczmy $|∡ P Q A| = α$ . Wtedy $|∡ A O R| = 2 α$ oraz $|∡ R A P| = 90 ° - \frac{1}{2} \cdot (180 ° - 2 α) = α$ . Ale to oznacza, na mocy cechy $k k k$ podobieństwa trójkątów, że trójkąty $P R A$ i $P A Q$ są podobne. Stąd, w szczególności $\frac{|A P|}{|P R|} = \frac{|P Q|}{|A P|}$ , czyli $|P Q| \cdot |P R| = {|P A|}^{2}$ .

Otrzymana zależność, która w programach szkolnych nosi nazwę twierdzenia o odcinkach stycznej i siecznej, jest szczególnym przypadkiem szerszego zagadnienia zwanego pod nazwą potęgi punktu względem okręgu. Aby je wprowadzić, wróćmy do naszego zagadnienia stycznej i siecznej, ale rozważmy sieczną, która zawiera średnicę okręgu, jak na rysunku.

R1OKcQfRsDNhZ

Na ilustracji przedstawiono okrąg o środku w punkcie O. Poprowadzono prostą, styczną do okręgu w punkcie A, oraz prostą przechodzącą przez środek okręgu i przecinającą okrąg w punkcie Q i R . Proste przecinają się w punkcie P. Zielonym kolorem zaznaczono odcinek AO, oraz OR. Różowym kolorem zaznaczono odcinek AQ, oraz AR. — Potęga punktu względem okręgu

Oznaczmy przez $r$ promień danego okręgu, a przez $d$ oznaczmy odległość $|O P|$ punktu $P$ od środka okręgu.

Wtedy $|P Q| \cdot |P R| = {|P A|}^{2} = d^{2} - r^{2}$ . Dla danego okręgu i danego punktu wielkość $d^{2} - r^{2}$ nazywamy potęgą punktu względem okręgu.

Okazuje się, że pojęcie potęgi punktu względem okręgupotęga punktu względem okręgupotęgi punktu względem okręgu można uogólnić na punkty leżące na okręgu (wówczas potęga jest równa $0$ ) oraz punkty wewnętrzne okręgu (potęga jest wtedy ujemna). Przydatne jest operowanie także pojęciem prostej potęgowejprosta potęgowaprostej potęgowej, która została pośrednio zdefiniowana w ćwiczeniach do niniejszej lekcji.

Pozostaje zapisać prosty wniosek, dotyczący różnych siecznych. Niech $Q$ , $R$ oraz $M$ , $N$ będą punktami, w których dwie różne sieczne przecinają odpowiednio dany okrąg, jak na rysunku.

R1Ys5LjyRC4o6

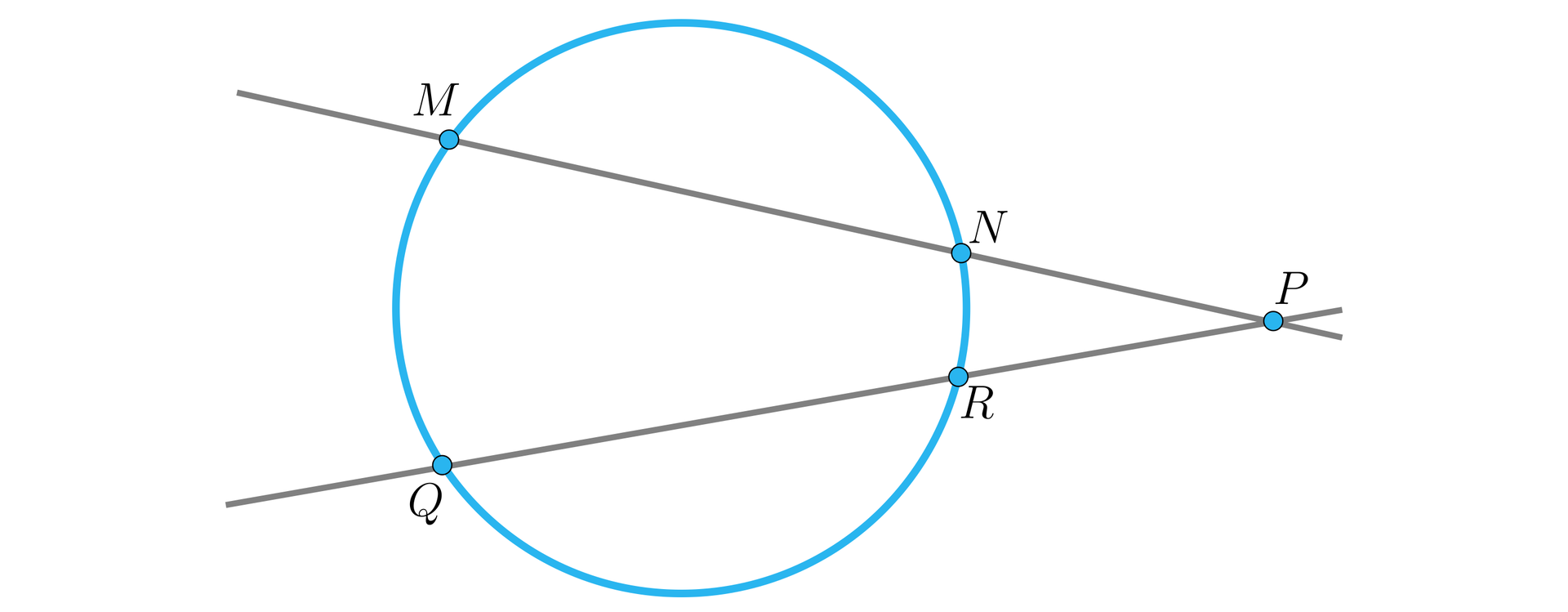
Na ilustracji przedstawiono okrąg. Poprowadzono dwie proste. Pierwsza prosta przecina okrąg w punkcie M i N. Druga prosta przecina okrąg w punkcie Q i R. Proste przecinają się w punkcie P. — Dwie sieczne.

Wtedy $|P Q| \cdot |P R| = |P M| \cdot |P N|$ .

Wróćmy teraz do zagadnienia ze wstępu do niniejszej lekcji. Pokażemy równość odcinków $A P$ i $B P$ , wyznaczonych na stycznych do dwóch przecinających się okręgów, jak na poniższym rysunku

R1VARqRPotow9

Na ilustracji przedstawiono dwa okręgi przecinające się w punktach Q i R, przez które przechodzi prosta. Poprowadzono prostą styczną do okręgu pierwszego w punkcie A, oraz styczną do okręgu drugiego w punkcie B. Trzy proste przecinają się w punkcie P. — Zastosowanie potęgi punktu względem okręgu.

Zauważmy, że $|P Q| \cdot |P R| = {|P A|}^{2}$ oraz $|P Q| \cdot |P R| = {|P B|}^{2}$ . Stąd wynika równość ${|P A|}^{2} = {|P B|}^{2}$ i postawiona teza.

Słowniczek

prosta potęgowa

dla niewspółśrodkowych okręgów zbiorem punktów, dla których ich potęga względem obu okręgów jest taka sama, jest prosta, którą nazywamy prostą potęgową lub osią potęgową

potęga punktu względem okręgu

dla danego punktu $P$ i dla danego okręgu o środku w punkcie $O$ i promieniu $r$ wyrażenie ${|P O|}^{2} - r^{2}$ nazywamy potęgą tego punktu względem danego okręgu

Wprowadzenie

Animacja

Zastosowanie twierdzenia o odcinkach stycznych

Potęga punktu względem okręgu

Słowniczek