RSqdCaxK9BJGC
Ilustracja przedstawia biurko na którym położono ołówek i ekierkę.

Własności figur geometrycznych na płaszczyźnie

Źródło: dostępny w internecie: Pexels.com, licencja: CC BY 3.0.

3. Kąty odpowiadające i naprzemianległe

Przybliżonym modelem prostych równoległych przeciętych trzecią prostą mogą być rozjazdy na torach kolejowych.

RXEpvRfgfZU0k1
Zdjęcie dwóch torów kolejowych połączonych rozjazdem.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Analizując przykłady zawarte w tym materiale poznasz kąty przy prostych równoległych przeciętych trzecią prostą i własności tych kątów. Rozwiązując ćwiczenia, utrwalisz poznane wiadomości.

Kąty odpowiadające i naprzemianległe
Definicja: Kąty odpowiadające i naprzemianległe

Proste k i l są równoległe względem siebie i przecięte prostą c.

  • Kąty: α i α1, β i β1, γ i γ1 oraz δ i δ1 to pary kątów odpowiadających.

  • Kąty α1 i δ oraz β1 i γ to pary kątów naprzemianległych wewnętrznych.

  • Kąty β i γ1 oraz α i δ1 to pary kątów naprzemianległych zewnętrznych.

    R6ys4nlFF3qis1
    Rysunek dwóch prostych równoległych k, l przeciętych trzecią prostą c. Między prostymi k i c oraz l i c, zaznaczono odpowiadające sobie kąty: kąty alfa i alfa z indeksem dolnym jeden, kąty beta i beta z indeksem dolnym jeden, gamma i gamma z indeksem dolnym jeden, delta i delta z indeksem dolnym jeden.
    Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
1
Przykład 1
Rnb7roFthdFIc
Animacja pokazuje dwie proste równoległe przecięte trzecią prostą. Między prostymi zaznaczone są cztery różne pary kątów odpowiadających.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DNuMQKmDt

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
1
Przykład 2
R1H8eFMu2pDcM
Animacja pokazuje dwie proste równoległe przecięte trzecią prostą. Między prostymi zaznaczono cztery różne pary kątów naprzemianległych.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DNuMQKmDt

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Kąty przy prostych równoległych
Twierdzenie: Kąty przy prostych równoległych

  • Jeżeli dwie proste równoległe przetniemy trzecią prostą, to tak utworzone kąty odpowiadające są równe.

    R1C45o8aPBbG41
    Rysunek prostych równoległych p i r przeciętych trzecią prostą. Między prostymi zaznaczone kąty odpowiadające alfa i beta. Kąty mają równe miary.
    Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

  • Jeżeli dwie proste równoległe przetniemy trzecią prostą, to tak utworzone kąty naprzemianległe wewnętrzne są równe oraz kąty naprzemianległe zewnętrzne są równe.

    RPLSJKLQT1pc11
    Rysunek prostych równoległych p i r przeciętych trzecią prostą. Między prostymi zaznaczone kąty naprzemianległe alfa i beta. Kąty mają równe miary.
    Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
1
Przykład 3
R1NzXV29r5327
Animacja pokazuje dwie proste równoległe, które zostały przecięte trzecią prostą. Między prostymi zaznaczone są cztery pary kątów naprzemianległych. Zmieniając położenie punktu P, leżącego na jednej z prostych równoległych, zmienia się położenie prostych równoległych i miary zaznaczonych kątów. Zaznaczone parami kąty naprzemianległe mają równe miary.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DNuMQKmDt

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
1
Przykład 4
RXDm0VH3ROiOA
Animacja pokazuje dwie proste równoległe a i b, które zostały przecięte trzecią prostą c. Między prostymi zaznaczona jest para kątów naprzemianległych alfa i beta. Na prostej a leży punkt. Zmieniając położenie punktu zmienia się położenie prostych równoległych i miary zaznaczonych kątów. Zaznaczone kąty naprzemianległe mają równe miary.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DNuMQKmDt

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
1
Przykład 5
Rp2tz4dxQ3fKd
Animacja pokazuje dwie proste równoległe a, b, które zostały przecięte trzecią prostą c. Między prostymi zaznaczona jest para kątów odpowiadających alfa i beta. Na prostej a leży punkt. Zmieniając położenie punktu zmieniamy położenie prostych równoległych i miary zaznaczonych kątów. Zaznaczone kąty odpowiadające mają równe miary.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DNuMQKmDt

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Równoległość prostych

1
Przykład 6
R15oVkjRPcIBp1
Animacja pokazuje dwie proste a i b przecięte trzecią prostą. Należy poruszając punktem P, leżącym na prostej b, obserwować położenie prostych a i b, gdy kąty naprzemianległe lub kąty odpowiadające mają takie same miary. Zauważamy, że jeżeli kąty naprzemianległe lub kąty odpowiadające mają równe miary, to proste a i b są równoległe.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DNuMQKmDt

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Dwie proste przecięte trzecią prostą 
Twierdzenie: Dwie proste przecięte trzecią prostą 

  • Jeżeli dwie proste przecięte są trzecią prostą i utworzone w ten sposób kąty odpowiadające są równe, to proste te są równoległe.

  • Jeżeli dwie proste przecięte są trzecią prostą i utworzone w ten sposób kąty naprzemianległe są równe, to proste te są równoległe.

Obliczanie miar kątów przy prostych równoległych

Przykład 7

Proste p i r są równoległe. Jeden z kątów wyznaczonych przez te proste ma miarę 57°. Obliczymy miary pozostałych kątów przy prostych p i r.

R1ZsqDgxaaSF81
Rysunek dwóch prostych równoległych p i r przeciętych trzecią prostą. Między prostymi zaznaczone osiem kątów. Prosta przecinająca utworzyła z prostą p kąty 1, 2, 3 i 57 stopni. Prosta przecinająca utworzyła z prostą r kąty 4, 5, 6, 7.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Kąt o mierze 57° i kąt 2 to kąty wierzchołkowe – ich miary są równe.

∢2=57°

Kąt o mierze 57° i kąt 7 to kąty odpowiadające przy prostych równoległych – ich miary są równe.

∢7=57°

Kąt 7 i kąt 5 to kąty wierzchołkowe – ich miary są równe.

∢5=∢7=57°

Kąt o mierze 57° i kąt 1 to kąty przyległe. Suma ich miar jest równa 180°.

∢1+ 57°=180°

Więc ∢1=123°
Pary kątów przyległych to również:
kąt 3 i kąt 2, kąt 7 i kąt 4 oraz kąt 6 i kąt 5.
Stąd

∢3=∢4=∢6=123°

Odpowiedź:

∢2=∢7=∢5=57°
∢1=∢3=∢4=∢6=123°
1
Ćwiczenie 1

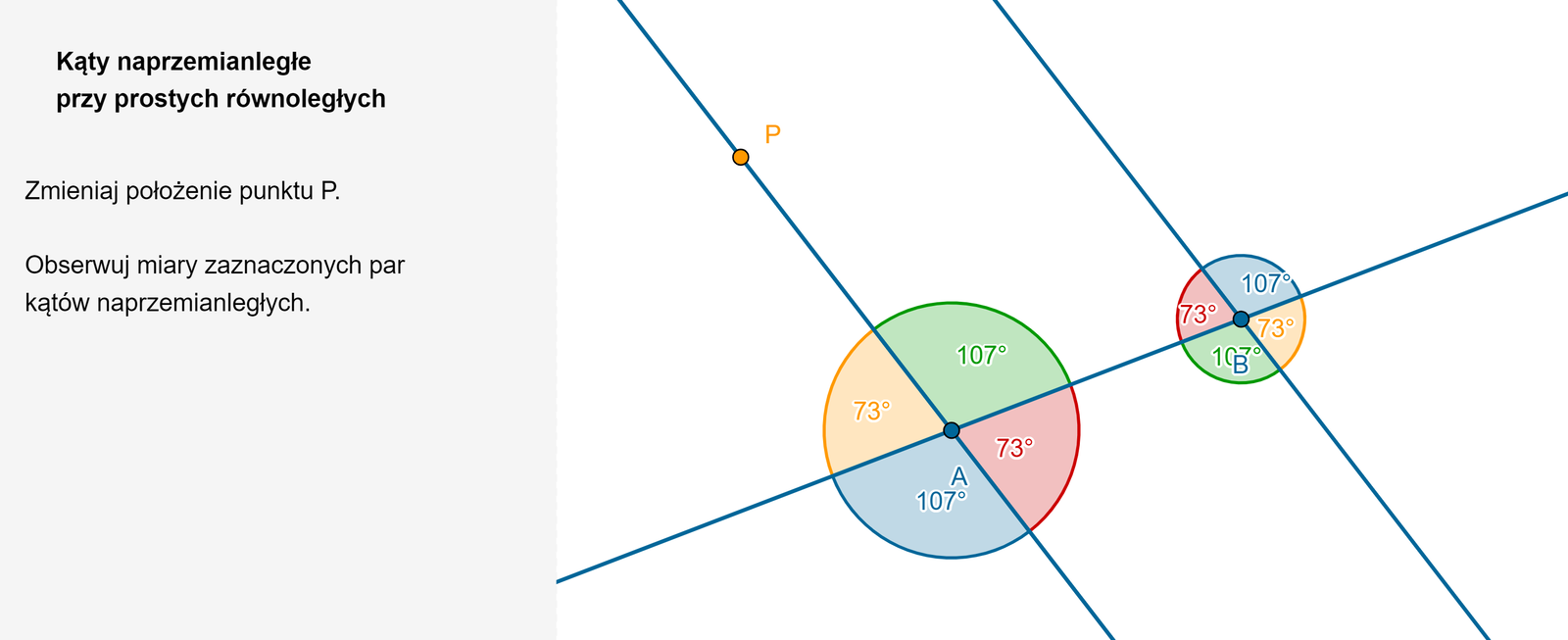
Podaj miary kątów przy prostych równoległych.

R177ESXLZwN6P1
Animacja pokazuje dwie proste równoległe przecięte trzecią prostą. Między prostymi zaznaczone osiem kątów. Należy, znając miarę kąta beta, podać miary pozostałych siedmiu kątów.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DNuMQKmDt

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RtYvn3B56NW2Y
Ćwiczenie 1
Dane są dwie proste równoległe p i r przecięte trzecią prostą k. Między prostymi zaznaczone osiem kątów. Prosta k utworzyła z prostą p kąty 1, 2, 3 i 4 stopni numerując je zgodnie z ruchem wskazówek zegara zaczynając od kąta po lewej stronie. Prosta k utworzyła z prostą r kąty 5, β, 6, 7 stopni numerując je zgodnie z ruchem wskazówek zegara zaczynając od kąta po lewej stronie. Uzupełnij miary wybranych kątów dla podanej miary kąta β. Kliknij w lukę aby rozwinąć listę i wybrać odpowiednią odpowiedź. Dla β=65°:
∢1= 1. 125°, 2. 65°, 3. 60°, 4. 30°, 5. 120°, 6. 150°, a ∢7= 1. 125°, 2. 65°, 3. 60°, 4. 30°, 5. 120°, 6. 150°.
Dla β=120°:
∢2= 1. 125°, 2. 65°, 3. 60°, 4. 30°, 5. 120°, 6. 150°, a ∢5= 1. 125°, 2. 65°, 3. 60°, 4. 30°, 5. 120°, 6. 150°.
Dla β=30°:
∢4= 1. 125°, 2. 65°, 3. 60°, 4. 30°, 5. 120°, 6. 150°, a ∢6= 1. 125°, 2. 65°, 3. 60°, 4. 30°, 5. 120°, 6. 150°.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 2

Proste p i r są równoległe. Uzupełnij zdania pod grafikami, przeciągając w luki odpowiednie miary kątów lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej.

1.

R1K5IiPlSxXRs
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1T0FI9f8mRV0
Kąt α ma miarę 1. 130°, 2. 70°, 3. 50°, 4. 100°, 5. 50°, kąt β ma miarę 1. 130°, 2. 70°, 3. 50°, 4. 100°, 5. 50°, a kąt γ ma miarę 1. 130°, 2. 70°, 3. 50°, 4. 100°, 5. 50°.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

2.

R14gghHKunFJp
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RaxlO7x9R0Ikx
Kąt α ma miarę 1. 85°, 2. 95°, 3. 95°, 4. 75°, 5. 70°, kąt β ma miarę 1. 85°, 2. 95°, 3. 95°, 4. 75°, 5. 70°, a kąt γ ma miarę 1. 85°, 2. 95°, 3. 95°, 4. 75°, 5. 70°.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1IjYtjf9d3fS
Ćwiczenie 2
Łączenie par. . Dwie proste równoległe p i r przeciętych trzecią prostą. Między prostymi zaznaczone kąty odpowiadające α i β. Kąty te mają równe miary. Zatem są to kąty:. Możliwe odpowiedzi: Wariant odpowiedzi 1, Wariant odpowiedzi 2. A. Możliwe odpowiedzi: Wariant odpowiedzi 1, Wariant odpowiedzi 2
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 3

Proste a i b są równoległe.

R1336pf147kOP
Rysunek prostych równoległych a, b przeciętych trzecią prostą. Między prostą przecinającą i prostą a zaznaczono kąty: 40 stopni, 1, 2 i 3. Między prostą przecinającą i prostą a zaznaczono kąty: 4, 5, 6, 7. Kąt 40 stopni jest kątem wierzchołkowym do kąta 2, kątem przyległym do kąta 1 oraz kątem odpowiadającym do kąta 5. Pary kątów 1 i 4, 2 i 7, 3 i 6 są odpowiadające.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1Sxem5loc6LT
Zaznacz zdanie prawdziwe. Możliwe odpowiedzi: 1. Miara kąta 1 jest równa 120°., 2. Miara kąta 6 jest równa 40°., 3. Miara kąta 5 jest równa 40°, 4. Miara kąta 4 jest równa 120°.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 4

Proste HA i GB są równoległe oraz proste KA i LC są równoległe.

RO25No5TG31H0
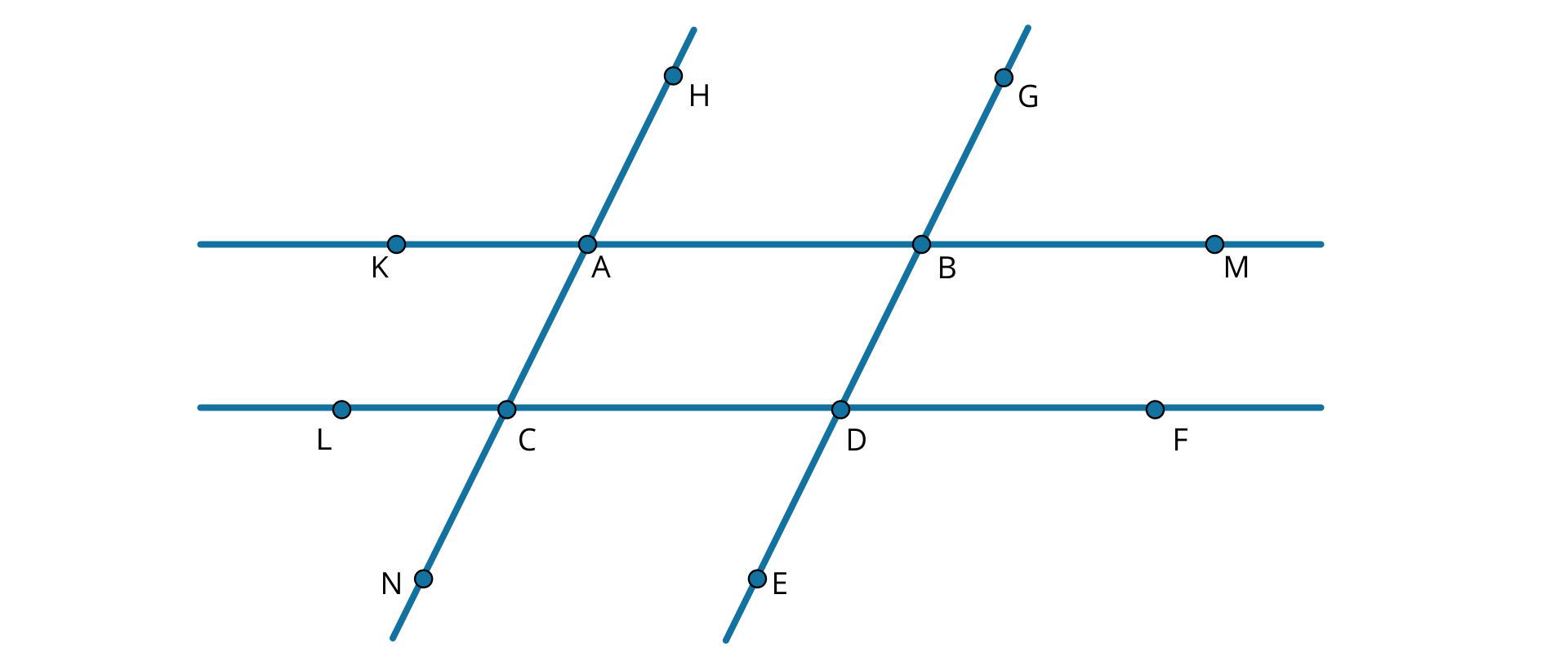
Na rysunku przedstawione są dwie proste równoległe KM oraz LF które zostały przecięte dwoma prostymi równoległymi do siebie HN oraz GE. Miejsce przecięcia prostej KM z prostą HN oznaczono punktem A, a przecięcie prostej LF z prostą HN oznaczono punktem C. Miejsce przecięcia prostej KM z prostą GE oznaczono punktem B, a miejsce przecięcia punktu LF z prostą GE oznaczono punktem D. Punkty przecięcia prostych leżą wewnątrz odpowiadających im odcinków HN, GE, KM i LF.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

  1. Wypisz wszystkie pary kątów naprzemianległych.

  2. Wypisz wszystkie pary kątów odpowiadających.

R7wHhCP9r9gJO
(Uzupełnij).
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 5
R13QygXRBBfmL
Proste równoległe m i s przecina prosta w. Jeden z kątów utworzonych przez proste w i s ma miarę 22°. Oblicz miary pozostałych kątów utworzonych przez proste w i m. Odpowiedzi wpisz w puste luki w kolejności rosnącej. Odpowiedź: Miary pozostałych kątów wynoszą Tu uzupełnij° oraz Tu uzupełnij°.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RamZhV9zw9Pnw
Ćwiczenie 6
Zaznacz wszystkie zdania prawdziwe. Możliwe odpowiedzi: 1. Kąty α i  β to para kątów odpowiadających przy prostych równoległych, przeciętych trzecią prostą. Zatem kąty te są równe., 2. Kąty γ i  δ to para kątów naprzemianległych przy nierównoległych prostych, przeciętych trzecią prostą. Zatem kąt γ jest dwa razy większy od kąta δ ., 3. Kąty μ i  φ to para kątów naprzemianległych przy prostych równoległych przeciętych trzecią prostą. Zatem kąty te są równe.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 7

Czy proste p i r są równoległe? Uzupełnij zdania, przeciągając w luki odpowiednie wyrażenia lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej.

1.

RL1yefX1rGSL3
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1YD1hg4UScvY
Te proste 1. nie są, 2. kąty naprzemianległe są równe, 3. są, 4. kąty wierzchołkowe są równe, 5. kąty odpowiadające nie są równe równoległe, ponieważ 1. nie są, 2. kąty naprzemianległe są równe, 3. są, 4. kąty wierzchołkowe są równe, 5. kąty odpowiadające nie są równe.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

2.

R1ABpn1MzagOK
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1OPYBdYucws0
Te proste 1. nie są, 2. kąty wierzchołkowe są równe, 3. kąty odpowiadające są równe, 4. są, 5. kąty odpowiadające nie są równe równoległe, ponieważ 1. nie są, 2. kąty wierzchołkowe są równe, 3. kąty odpowiadające są równe, 4. są, 5. kąty odpowiadające nie są równe.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RnwTrCAklsFQ9
Ćwiczenie 7
Poniżej podano rodzaje kątów i ich pary między prostymi. Przeciągnij opisy kątów do odpowiedniej kategorii. są równoległe Możliwe odpowiedzi: 1. kąty α i β są parą kątów odpowiadających, gdzie ∢α=60° oraz ∢β=60°
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 8

Proste a i b są równoległe.

RgCRSEnc83k1Y
Rysunek dwóch poziomych prostych równoległych a i b przeciętych trzecią prostą. Między prostą przecinającą i prostą a zaznaczono kąty: 1, 2, 3 i 4 odpowiednio numerując lewy górny kąt, prawy górny, lewy dolny kąt, prawy dolny. Między prostą przecinającą i prostą b zaznaczono kąty: 5, 6, 7, 8 numerowane jak poprzednio. Pary kątów 1 i 5, 2 i 6, 3 i 7, 4 i 8 to kąty odpowiadające. Kąt 1 jest kątem wierzchołkowym do kąta 4 i kątem przyległym do kąta 2.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1KlIwazjWY3b
Oblicz ∢1, a następnie uzupełnij zdania, przeciągając w luki odpowiednie miary kątów lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. Kiedy miara kąta 2 jest o 20° większa od miary kąta 1, to miara kąta 1 wynosi 1. 80°, 2. 80°, 3. 86°, 4. 72°.Kiedy ∢2+∢7=200°, to miara kąta 1 wynosi 1. 80°, 2. 80°, 3. 86°, 4. 72°.Kiedy ∢7-∢5=8°, to miara kąta 1 wynosi 1. 80°, 2. 80°, 3. 86°, 4. 72°.Kiedy ∢6=108°, to miara kąta 1 wynosi 1. 80°, 2. 80°, 3. 86°, 4. 72°.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 9

Oblicz miary kątów równoległoboku, korzystając z własności kątów przy prostych równoległych.

R8gM5GuyNNssZ1
Rysunki dwóch równoległoboków. W pierwszym równoległoboku zaznaczony kąt 70 stopni, który jest kątem wierzchołkowym do jednego z kątów wewnętrznych równoległoboku. W drugim równoległoboku zaznaczony kąt 85 stopni, który jest kątem przyległym do jednego z kątów wewnętrznych równoległoboku.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RvYrwIEueL7sz
(Uzupełnij).
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RjrTeZMiMGTvc
Ćwiczenie 9
Zapoznaj się z poniższymi opisami równoległoboków. Wyznacz odpowiednie miary katów. Kliknij w luki aby rozwinąć listę, a następnie wybierz prawidłową odpowiedź. Dany jest równoległobok, którego dwa sąsiednie boki zostały przedłużone, a kąt między nimi jest równy 70°. Wynika stąd, że:
kąt ostry w równoległoboku ma miarę 1. 110°, 2. 46°, 3. 70°, 4. 134°.
kąt rozwarty w równoległoboku ma miarę 1. 110°, 2. 46°, 3. 70°, 4. 134°.
Dany jest równoległobok, którego podstawa została przedłużona. Kąt między pomiędzy ramieniem równoległoboku, a przedłużeniem boku wynosi 46°. Wynika, stąd, że:
kąt ostry w równoległoboku ma miarę 1. 110°, 2. 46°, 3. 70°, 4. 134°.
kąt rozwarty w równoległoboku ma miarę 1. 110°, 2. 46°, 3. 70°, 4. 134°.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 10

Uzasadnij, że:

  1. dwie proste równoległe do trzeciej prostej są do siebie równoległe

  2. dwie proste prostopadłe do tej samej prostej są do siebie równoległe

  3. przeciwległe kąty równoległoboku są równe

R160LvDRVHvsB
(Uzupełnij).
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Notatnik

Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.

R1b8OvSPUG8s3
(Uzupełnij).
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
2. Kąty wierzchołkowe i przyległe
4. Przystawanie figur