System dwójkowy
System dwójkowy pozycyjnySystem dwójkowy pozycyjny umożliwia komputerom przetwarzanie i przechowywanie informacji. W komputerach informacja jest zapisywana i przechowywana binarnie ze względu na charakter elektroniczny (dwustanowość)charakter elektroniczny (dwustanowość). Do zapisu liczb w systemie dwójkowym wykorzystywane są dwie cyfry 0 i 1, co umożliwia szybkie przetwarzanie informacji.
Interaktywna treść merytorycznaInteraktywna treść merytoryczna
MultimediumMultimedium
Zestaw ćwiczeń interaktywnychZestaw ćwiczeń interaktywnych
SłownikSłownik
BibliografiaBibliografia
Omówisz sposób zapisu liczb w dwójkowym systemie pozycyjnym.
Wykonasz podstawowe działania arytmetyczne z wykorzystaniem systemu dwójkowego.
Wyjaśnisz zastosowanie standardu ASCIIASCII do przechowywania informacji o znakach w komputerze.
W pozycyjnym systemie liczbowympozycyjnym systemie liczbowym cyfry mają różne znaczenie w zależności od miejsca, jakie zajmują w liczbie. Inne systemy pozycyjne niż dziesiętny, z którego korzystamy na co dzień do różnych obliczeń np. w matematyce i fizyce, możemy spotkać w różnych naukach technicznych, a zwłaszcza w informatyce – są to systemy dwójkowy i szesnastkowy. Istnieją również inne systemy.
Określeń cyfra i liczba nie należy ze sobą mylić. Cyfra to umowny znak służący do zapisywania liczb. Podobnie jak wyraz składa się z wielu liter, tak liczba może składać się z wielu cyfr.
Działanie komputera i jego podzespołów możemy opisać przy pomocy sekwencji liczb.
Porusz myszką – kursor wykonuje ruch na ekranie. Ruch myszką jest odczytywany przez komputer, który przekształca go na cyfrowe wartości i oblicza przemieszczenie kursora na ekranie. Następnie aktualizuje pozycję kursora i wyświetla go na ekranie.
Komputery, a właściwie procesoryprocesory (bo to one dokonują obliczeń), posługują się stanami logicznymistanami logicznymi w celu przetwarzania informacji, które bardzo łatwo interpretować jako cyfry:
0 - stan niski (brak prądu),
1 - stan wysoki (jest prąd).
W pozycyjnym systemie dwójkowympozycyjnym systemie dwójkowym liczby są zapisywane jako ciągi cyfr 0 i 1. Każda pozycja 0 lub 1 w liczbie odpowiada potędze dwójki, zaczynając od najmniej znaczącej cyfry, której odpowiada potęga 2Indeks górny 00. Na przykład, liczba 1011 w pozycyjnym systemie dwójkowym odpowiada liczbie 11 w pozycyjnym systemie dziesiętnym:
Oto kilka przykładów liczb zapisanych w systemie binarnym, kolejne wartości potęgi 2 oraz odpowiadające im liczby w systemie dziesiętnym:
Liczba binarna | liczba dziesiętna | |||
|---|---|---|---|---|
| 0 | 0 | 0 |
|
| 0 | 0 | 1 |
|
| 0 | 2 | 0 |
|
| 0 | 2 | 1 |
|
| 4 | 0 | 0 |
|
| 4 | 0 | 1 |
|
| 4 | 2 | 0 |
|
| 4 | 2 | 1 |
|
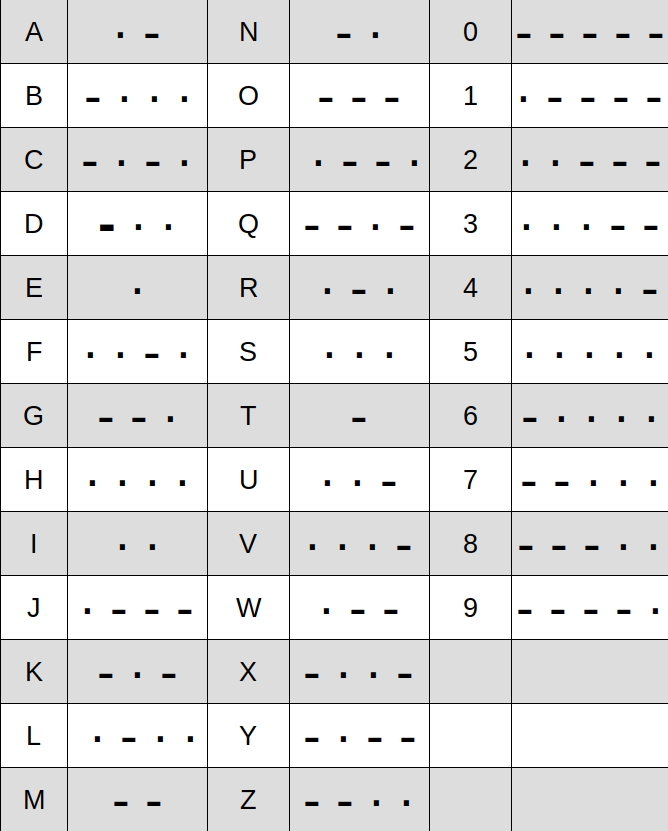
Alfabet Morse'a, którego używa się w radiokomunikacji i w nawigacji morskiej, jest podobny do systemu binarnegosystemu binarnego. Do zapisu każdego znaku wykorzystuje sekwencję kropek i kresek. Jednym z najbardziej znanych jest sygnał alarmowy SOS (ang. save our ship, save our souls).

Sygnał składa się z trzech kropek, trzech kresek i znów trzech kropek.

Podstawowe operacje arytmetyczne
Porównując operacje w systemie dwójkowym i dziesiętnym, możemy dostrzec pewne podobieństwa. W obu systemach jeśli suma jest dwucyfrowa (np. 8 + 3 = 11), to pod kreską zapisujemy tylko ostatnią cyfrę 1, a 1 przechodzi do następnej kolumny - dodamy ją do wyniku sumowania cyfr w następnej kolumnie. Jest to tzw. przeniesienie. Wykorzystujemy je, wykonując działania pisemnie (w słupku).
Dodawanie liczb binarnych
O ile w przypadku systemu dziesiętnego sumowanie dwóch liczb, np. 11 i 13, nie sprawi nam kłopotu, o tyle w przypadku systemu binarnego dodanie do siebie 1011 oraz 1101 nie wydaje się już tak oczywiste.
Do wykonania działania możemy wykorzystać reguły, które stosujemy w przypadku dodawania pisemnego. Musimy jednak pamiętać, że podstawą tego systemu jest 2, nie 10. Ponadto wykorzystujemy tylko dwie cyfry: 0 i 1.
Zasady ich dodawania są następujące:
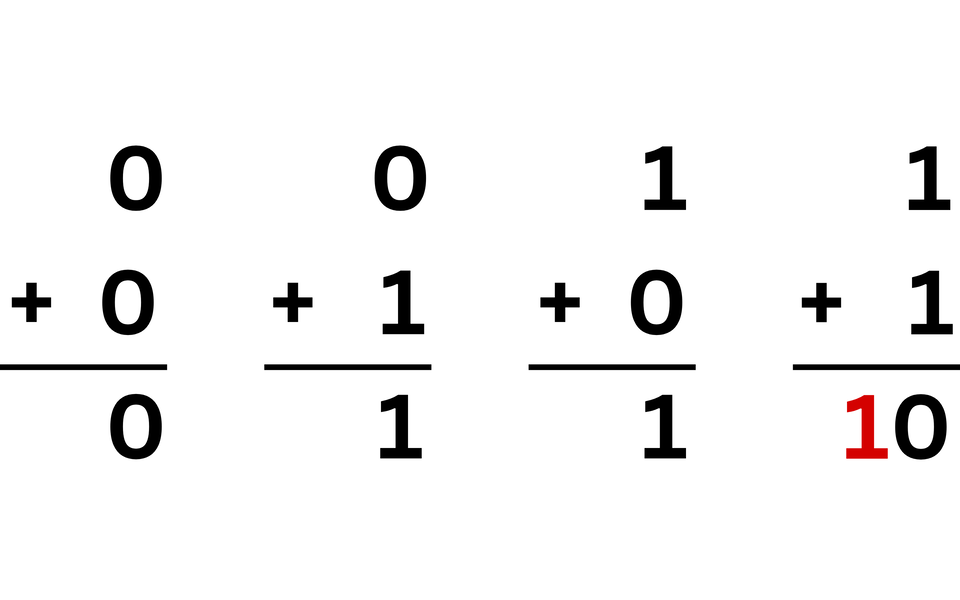
Kiedy w systemie dwójkowym dodajemy do siebie dwie liczby 1, uzyskujemy wynik 10. Dzieje się tak, ponieważ jedna z 1 jest dodawana do wartości następnej kolumny po lewej stronie. Podobnie robimy, sumując liczby w systemie dziesiętnym – dodajemy odpowiednią wartość (przenosimy) do wartości cyfry bardziej znaczącej (po lewej stronie), gdy suma dwóch cyfr mniej znaczących przekracza 9.
Dodawanie liczb binarnych zaczynamy od dodawania najmniej znaczących bitów. Używamy opisanych zasad dodawania bitów, a dodatkowo:
jeśli suma wynosi
10, zapisujemy0i dodajemy1do następnej kolumny po lewej stronie;jeśli suma wynosi
11, zapisujemy1i dodajemy1do następnej kolumny po lewej stronie – taka sytuacja może się wydarzyć, kiedy musimy dodać jeszcze przeniesioną cyfrę.
Przeanalizujemy przykład.
Oto dodawanie:
Mnożenie liczb binarnych
Mnożnik zapisujemy pod mnożną, a potem mnożąc każdą cyfrę przez każdą, wyniki częściowe zapisujemy podobnie jak w pozycyjnym systemie dziesiętnym. Ostatecznie sumujemy otrzymane liczby.
Przypomnijmy sobie sposób mnożenia dwóch liczb naturalnych większych od 10 - widzimy tu wyniki częściowe (48 i 12), a potem ich sumę, czyli wynik mnożenia:
Zasady mnożenia bitów w liczbach binarnych są następujące:
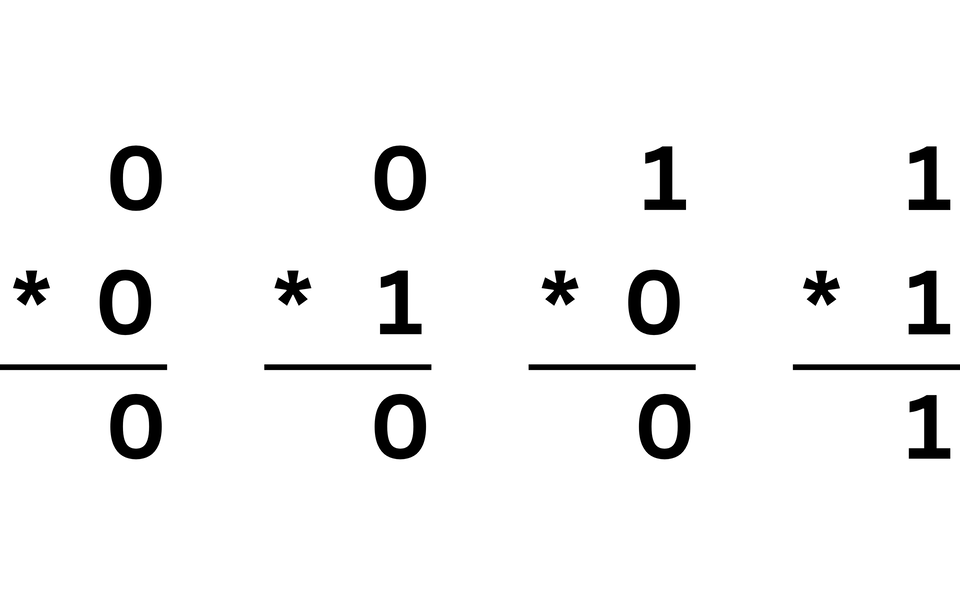
Wyrównanie liczb: Zaczynamy od napisania dwóch liczb binarnych jedna pod drugą tak, aby ich bity były wyrównane od prawej do lewej. Najmniej znaczące bity znajdują się na prawym końcu, a najbardziej znaczące bity na lewym końcu.
Rozpoczynamy mnożenie bitów: Zaczynając od prawej kolumny dolnej liczby, mnożymy każdy bit przez każdy bit górnej liczby. Zapisujemy wynik pod linią, kolejne iloczyny zaczynamy zapisywać pod bitem, przez który mnożymy.
Dodajemy wyniki: Po pomnożeniu każdego bitu dolnej liczby przez górną liczbę dodajemy wszystkie wyniki w poszczególnych kolumnach. Pamiętajmy o tym, że dodawanie w systemie binarnym może wymagać przeniesienia, jeżeli suma bitów w jednej kolumnie przekroczy 1.
Po dodaniu wszystkich wyników, wynik pod poziomą kreską to iloczyn dwóch liczb binarnych.
Przeanalizujemy przykład.
Oto operacja mnożenia:
Odejmowanie liczb binarnych
Odejmowanie zapisujemy analogicznie jak dodawanie metodą pisemną. Zaczynamy od najmniej znaczących cyfr.
Zapoznaj się z ilustracją przedstawiającą zasady odejmowania w dwójkowym systemie pozycyjnym:
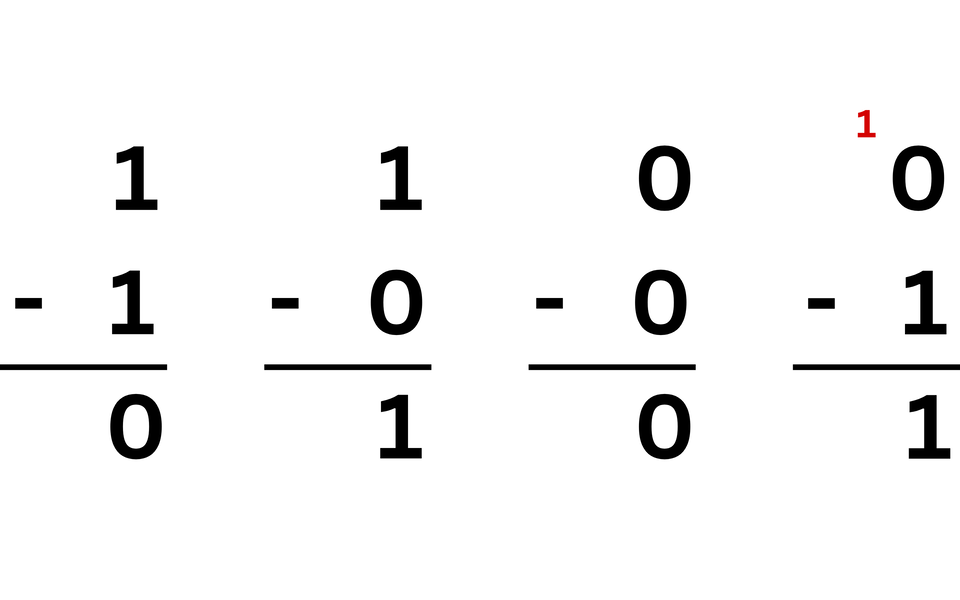
Bity i bajty – system binarny w komputerach
Zera i jedynki użyte w zapisie binarnym nazywane są bitami informacji i reprezentują stany logicznestany logiczne. 8 bitów to 1 bajt. Jeden bajt pozwala na zapis 256 różnych wartości. Bajty i ich wielokrotności są używane do oznaczenia wielkości pamięci w urządzeniach komputerowych. W takich jednostkach podajemy pojemność pamięci operacyjnej RAMpamięci operacyjnej RAM w komputerze oraz wielkość dysków twardych i innych nośników danych.
Nazwa | Liczba wyrażona w wielokrotności jednostki | Liczba bajtów |
|---|---|---|
bajt (B) | 8 bitów |
|
kilobajt (KB) | 1024 bajty |
|
megabajt (MB) | 1024 kilobajty |
|
gigabajt (GB) | 1024 megabajty |
|
ASCII – standard kodowania znaków
Znaki, takie jak litery, cyfry i symbole specjalne są reprezentowane w komputerze przy pomocy liczb. Każdemu znakowi przypisana jest odpowiadająca mu wartość. Ten sposób przypisania znaku do liczby nazywamy kodowaniem. Najczęściej używanym systemem kodowania jest kod ASCIIkod ASCII (ang. American Standard Code for Information Interchange), który jest standardowym systemem kodowania znaków w komputerach (w ASCII znak wykorzystuje 1 bajt). Kody dziesiętne od 0 do 31 są to tzw. kody sterujące, które niosą pewne informacje dla komputera, a nie widać ich na monitorze ani na wydruku.
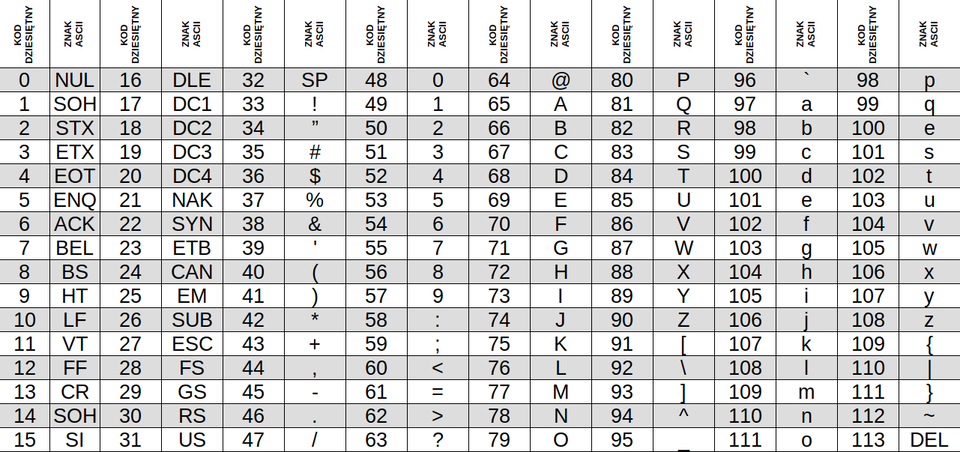
Kod ASCIIKod ASCII reprezentuje każdy znak jako pewną liczbę. Na przykład, litera „A” jest kodowana jako 100 0001 (w systemie binarnym), co odpowiada liczbie 65 w systemie dziesiętnym. Każdy znak w kodzie ASCII jest przypisany do unikalnej wartości liczbowej, co umożliwia komputerom przetwarzanie i wymianę informacji tekstowej. Kod ASCII jest nadal używany w wielu systemach, ale istnieją również inne systemy kodowania, takie jak UnicodeUnicode, które pozwalają na reprezentację większej liczby znaków i symboli z różnych języków i kultur.
Notatnik
Prezentacja multimedialna
Indeks górny Źródło: Adam Jurkiewicz, licencja: CC BY 3.0. Indeks górny koniecŹródło: Adam Jurkiewicz, licencja: CC BY 3.0.
Zestaw ćwiczeń interaktywnych
0, a kreska to bit o wartości 1 to jak będzie wyglądał kod binarny znanego sygnału wezwania pomocy SOS (trzy kropki, trzy kreski, trzy kropki)? Zaznacz poprawną odpowiedź. Możliwe odpowiedzi: 1. 101010101, 2. 000111000, 3. 111000111Dana jest liczba zapisana w systemie dwójkowym. W języku Scratch zapisz program, który obliczy liczbę cyfr 0 w liczbie zapisanej w pozycyjnym systemie dwójkowym. Program powinien wypisać wynik na ekranie.

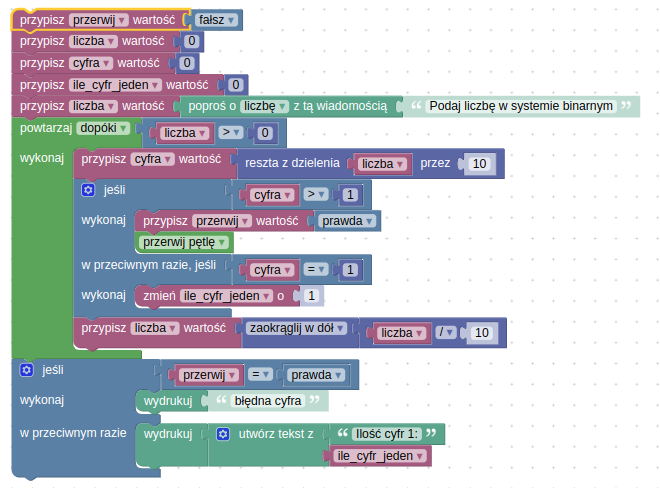
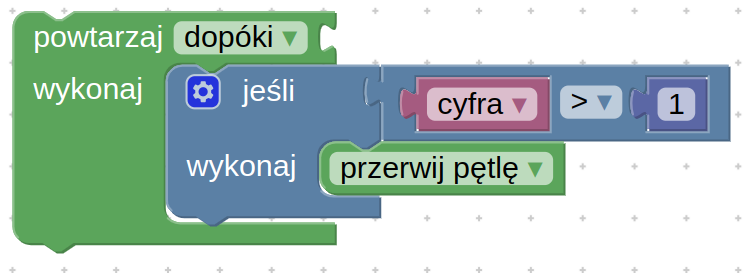
W Blockly wykonaj program, który obliczy liczbę cyfr 1 w liczbie w pozycyjnym systemie dwójkowym i wypisze na ekranie, informację o obliczonej liczbie, np.:

Program powinien również sprawdzać, czy wprowadzona liczba to liczba w systemie binarnym, czyli czy żadna z jej cyfr nie jest większa od 1. Jeśli liczba nie jest zapisana w systemie binarnym, program powinien wyświetlić komunikat błędna cyfra i przerwać działanie programu.
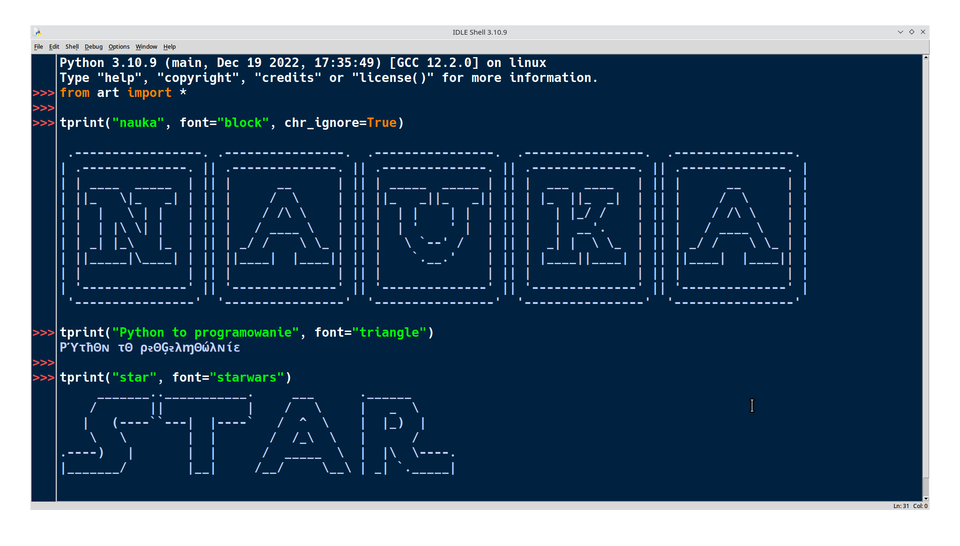
Blockly generuje automatycznie odpowiednik kodu w języku Python, jednak często zawiera on zbędne elementy. W przypadku kodu z ćwiczenia 7 możemy usunąć część instrukcji.
Kod z którego usunęliśmy zbędne instrukcje:
Słownik
standardowy system kodowania znaków, który jest używany w komputerach i urządzeniach elektronicznych; podstawowy kod ASCII składa się z 128 znaków, w tym liter alfabetu łacińskiego, cyfr, znaków interpunkcyjnych i kontrolnych; jest używany do przechowywania i przetwarzania tekstów w komputerach i jest uważany za podstawę wielu innych systemów kodowania znaków, takich jak UTF‑8 i Unicode
(ang. Random Access Memory) rodzaj pamięci komputerowej, która służy do przechowywania danych tymczasowych, na których operuje procesor; jest niezbędna do uruchamiania programów, szybkiego odczytu i zapisu informacji, co przyspiesza działanie komputera
system liczbowy, w którym wartość cyfry zależy od pozycji, na której jest zapisana, np. w dziesiętnym systemie w liczbie 123 cyfra 2 oznacza liczbę dziesiątek, a więc wartość 20
elektroniczny układ scalony odpowiedzialny za wykonywanie instrukcji i obliczeń w komputerze; wykonuje podstawowe operacje (dodawanie, odejmowanie, mnożenie i dzielenie) oraz zarządza przepływem danych i instrukcji wewnątrz komputera; procesory składają się z wielu mikroprocesorów, zwanych rdzeniami, które są zdolne do wykonywania wielu instrukcji jednocześnie
elektroniczna reprezentacja Prawdy lub Fałszu, których odpowiednikiem są 1 lub 0 w układach scalonych komputerów
inaczej system dwójkowy; system liczbowy oparty na dwóch cyfrach: 0 i 1; jest to podstawowy system wykorzystywany w elektronice cyfrowej oraz w komputerach
(ang. Unicode Standard) - standard kodowania znaków, który przypisuje każdemu znakowi (literze, cyfrze, symbolowi) unikalny numer; jest powszechnie używany w różnych systemach informatycznych, aby zapewnić spójność i jednoznaczność kodowania znaków na całym świecie
w elektronice cyfrowej, jednostkach pamięci i obliczeniach komputerowych, informacje są przechowywane i przetwarzane za pomocą dwóch stanów logicznych: 0 to brak sygnału, 1 oznacza obecność sygnału, np. w transmisji danych
Bibliografia
Dokumentacja języka Python, docs.python.org, dostęp: 19.04.2024.
Gra w życie, pl.wikipedia.org, dostęp: 19.04.2024.
Jurkiewicz A., Python 3 - Projekty dla początkujących i pasjonatów, Helion, Gliwice 2021.
Petzold Ch., Kod. Ukryty język komputerów, Helion, Gliwice 2021.
Sysło M., Algorytmy, Helion, Gliwice 2016.
Wałaszek J., Operacje arytmetyczne w systemie dwójkowym, eduinf.waw.pl, dostęp: 19.04.2024.





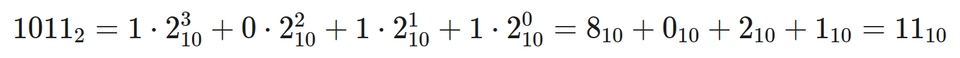
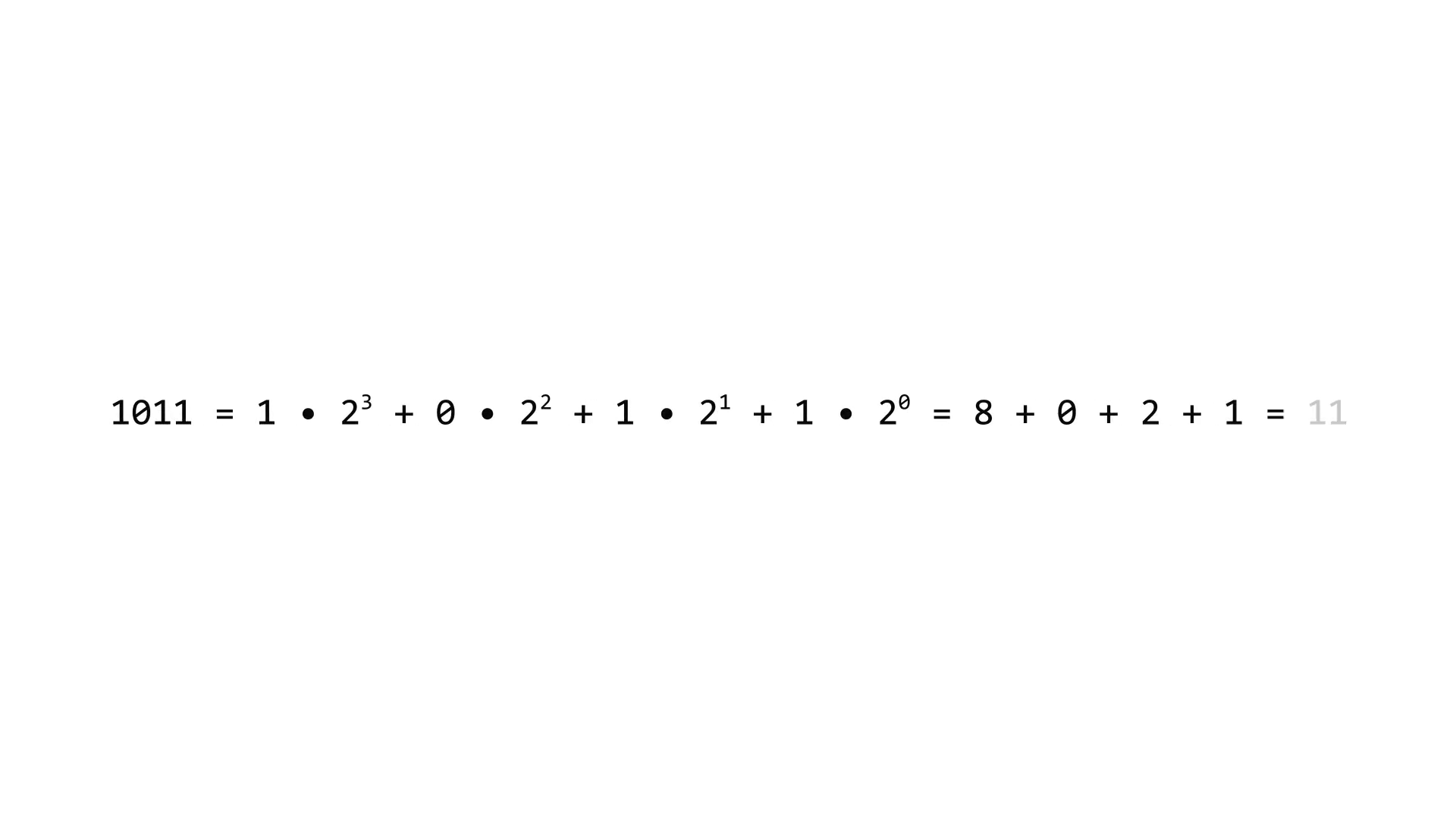



![Na grafice znajduje się program stworzony w języku wizualnym Scratch, zbudowany z kolorowych bloków ułożonych pionowo. Program rozpoczyna się blokiem „kiedy kliknięto zieloną flagę”. Następnie ustawiane są trzy zmienne: „liczba”, „cyfra” i „ile_cyfr” na 0. Program wyświetla użytkownikowi pytanie w niebieskim bloku: „Podaj liczbę w systemie binarnym i czekaj”. Odpowiedź użytkownika zostaje przypisana do zmiennej „liczba”.
W dalszej części znajduje się pętla „powtarzaj aż [liczba = 0]”. W jej wnętrzu:
Wyznaczana jest ostatnia cyfra liczby jako reszta z dzielenia przez 10 i przypisywana do zmiennej „cyfra”.
Jeśli „cyfra” równa się 0, zmienna „ile_cyfr” zwiększa się o 1.
Następnie liczba jest dzielona przez 10 (po odjęciu cyfry), co pozwala przejść do kolejnej cyfry.
Po zakończeniu pętli fioletowy blok „powiedz” wyświetla przez 2 sekundy komunikat: „Liczba cyfr 0:” oraz wartość zmiennej „ile_cyfr”.](https://static.zpe.gov.pl/portal/f/res-minimized/R1R972U9AtuW8/1751354276/2Y6zsF8buqF2G4RPkPRjsgJGMRD9Gvex.png)